定义1 设三维几何空间为R, 用三维几何坐标系统F_W表示。在F_W中用F_A表示模型A所占的集合, 则F_A是F_W的子集。T={T₁, T₂, T₃, …, T_n}为时间集, T_i表示时间集上的任意时刻, F_W随着T变化的四维空间坐标系统C_W, 模型A沿着一定轨迹运动够成C_W的子集表示为C_A。碰撞检测就判断空间坐标系统C_W的子集C_A是否为空集, 即 CT1∩ CT2∩ …∩ CTn≠ ∅是否成立。这个定义在实质上给出了碰撞检测的精确描述过程, 要实现这一描述过程, 代价非常高, 解决的关键问题是四维集合C_A的计算。

碰撞检测过程就是判断空间任何两个几何体之间是否存在相交的过程, 而空间几何体的划分多以三角形为主, 因此相交检测的过程就是三角形与三角形求交的过程。文献[6]提出了矢量判别法和标量判别法两种判别三角形相交的算法, 并通过实验证明了矢量判别法比标量判别法速度快7%, 本文以此算法设计了基本碰撞检测算法, 并采用k-Dop包围盒及并行化的SIMD-Dop的方法实现三角形的求交过程。

在碰撞检测中最常用的技术就是包围盒相交检测技术。目前常用的包围盒技术有包围球、AABB、OBB、k-DOP等, 每一种包围盒都有其各自的优缺点和适用范围。k-DOP即为离散有向多面体(Discrete oriented polyhedron, k-DOP)。

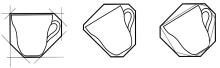
由于k-DOP的平面方向是固定的, 包围盒逼近效果比较好, 几何体重叠相交测试速度快, 所以本文选择k-DOP为碰撞检测层次中的包围体, 随着k的增大, k-DOP与物体的凸包越来越相似, 测试表明, 选k=18时具有最好的效率。如图1所示, 是一个茶杯的8-DOP示例。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 一个茶杯的二维8-DOPFig.1 Two-dimensional 8-DOP of a cup

k-DOP其实是介于AABB和凸包之间的包围盒, 其突出特点是只要合理地选取平行平面对的个数和方向, 就可以在碰撞检测的简单性和包裹物体的紧密性之间灵活取舍, 即紧密性要优于AABB, 而相交测试的复杂度要小于OBB。由于k-DOP包围盒间相交测试的速度是所有包围盒类型中最快的相交测试, 所以本文采用的检测包围盒选择了k-DOP包围盒。鉴于此, 本文提出了一种新的构建k-DOP平衡包围盒树的方法。具体构建方法如下:

(1)任取空间解集M={M₁, M₂, …, M_n}的任意两个物体M_i∈ M, M_j∈ M, 分别以M_i, M_j为根节点构建其整体k-DOP包围盒树, M_i, M_j包含组成物体所有多边形。

(2)采用文献[7]分裂平面的方法划分M_i, M_j的左右子树。

(3)使用最长轴方法确定分裂轴、分裂点, 然后确定根节点M_i, M_j中所有几何元素的中心点在分裂轴上的投影。

(4)找出最大点和最小点, 并以这两个点为中心点, 将距离投影点分为两组。若有点距两中心点等距, 则将其归入含投影点少的一组。

(5)递归执行上述过程, 直到满足线性判别函数P(x)=* M_j的递归终止条件。其中M_i=(M_i1, M_i2, …, M_in), M_j=(M_j1, M_j2, …, M_jn)。M_j1, M_j2, …, M_jn为递归终止条件, 可以是包围盒树高度, 叶子节点中所含基本几何元素的最多数等, M_i1, M_i2, …, M_in分别为M_j1, M_j2, …, M_jn对应的加权值。

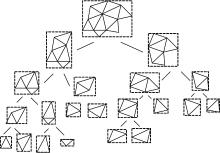
设M_i∈ M, M_j∈ M是空间解集M={M₁, M₂, …, M_n}的任意两个元素, 不妨设M_i, M_j是构建包围盒树的两个根节点, 按照1.3节k-DOP平衡包围盒树构造方法构造两颗平衡包围盒树。则以M_i, M_j为根节点的平衡包围盒树包含组成物体所有多边形。其划分过程如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 划分为几何体的平衡包围盒树Fig.2 Divided into geometry balance bounding box tree

定理1 任取空间解集 M={M₁, M₂, …, M_n}的任意两个物体M_i∈ M, M_j∈ M, δ =D(M_i, M_j)为两个物体间距δ ≥ 0, 若两物体之间存在一特征点M_{i, j}(M_i, M_j), 满足D(M_i, M_j)≤ δ , 当δ = limx→∞(minD(M_i, M_j))=0则M_i, M_j一定相交。

证明:假设M_i, M_j不相交, 则一定存在一个特征点 M-i, j( M-i, ), 满足D( M-i, M-j)≤ , 使得< δ 成立, 由于δ = limx→∞(minD(M_i, M_j))=0, 必有< 0, 矛盾, 故定理成立。

所以在随机碰撞检测中, 若判断两个物体是否相交, 就是要判断两个物体之间是否存在一特征点M_{i, j}(M_i, M_j), 满足D(M_i, M_j)≤ δ 。若存在这样的特征点, 则两物体发生碰撞。M_i, M_j是两物体物体的基本几何元素包围盒特征, 它们在物体空间具有坐标属性(x, y, z), D为距离函数, δ 为距离阈值, 为了能找到满足条件的特征对集合, 本文把问题转化为一个由两模型特征对序号构成的离散二维空间中的优化问题, 并将优化算子引入蚁群优化算法求解, 从而返回模型间的碰撞点。搜索空间M是由两模型特征对任意组合形成的二维离散空间, 并且M的大小为M_i× M_j。构建的搜索空间是一个多峰值的动态空间, 这是因为在物体空间中, 发生碰撞的两个物体可能产生多个碰撞点, 把它描述在搜索空间中即是存在多个极值, 另外在搜索空间中最优解位置变化也会引起搜索空间动态变化。

对于中小规模的应用问题, 蚁群算法可以在允许的时间范围内获得满意的解。对于大规模或超大规模多变量的求解问题, 简单的串行蚁群算法由于可能会出现早熟现象, 从而影响求解过程^[8]。近年来出现了一些并行蚁群算法或将串行算法并行化^[9], 其目的不只是为了缩短算法的执行时间, 更多的是为了维持群体多样性的能力, 避免算法出现早熟。

为了避免蚁群陷入局部最优解, 本文提出了优化算子的概念。

优化算子:首先将该子种群τ ₀和τ _max初始化为τ ₀=τ _max=1/ (1-ρ)Lgb, τ _min=τ _max/(2n), 式中L_gb为至此所有子种群的最优路径的长度, ρ 为种群参数, 参数的确定取决于种群。从全局最优解中心随机选出m个解, 更新信息素矩阵, 一般情况下取mM的乘积。各边信息素值按如下递归方式更新:

τij=(1-ρ)τij+ρ·∑k=1mckrkΔτijk(1)

其中:

Δ = (Sk)-1, (i, j)为选出的第k个解路径0, 否则

S_k表示选出的第k个解的路径长度, r_k为[0, 1]之间均匀分布的随机数, c_k为Δ 的权重值, 由于r_k的期望均值为1/2, 所以 ∑k=1mc_k=2。

对于子种群参数α 、β 和ρ 采用算术交叉方式完成初始化如下:

α=∑k=1mckrkαk2β=∑k=1mckrkβk3ρ=∑k=1mckrkρk4

其中, r_k和c_k为初始化信息素时保留值。而α _k、β _k和ρ _k则为选出的第k个解所使用的运行参数。

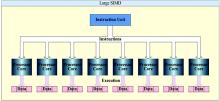
SIMD是在单一控制部件下的多个处理单元构成的阵列, 所以有时也称为阵列处理机。SIMD技术主要用于大量高速向量或矩阵运算的场合。SIMD重复设置多个同样的处理单元(Processing element, PE), 按照一定的方式相互连接, 在统一的控制器控制下, 各自对分配来的数据并行地完成同一条指令所规定的操作。可以提高数据同时运算的效率, 这个特点使SIMD技术特别适合计算密集型的应用, 如三维游戏动画、实时仿真等。如图3所示。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 SIMD并行处理机模型Fig.3 SIMD parallel processor model

(1)基于SIMD指令的k-DOP优化

k-DOP是由多组平行面定义的3D空间封闭区域。每组中的两个平行平面限定了物体在平面法向方向上的延伸范围。k-DOP提供了相对AABB更加紧凑的包围盒并且与OBB相比进行构造和整理的代价较小^[10]。

通过使用SIMD浮点向量保持所有数据, 我们可以使用SIMD指令对SIMD-DOP重建、整理、重叠测试进行加速, 在k-DOP包围盒树的重建、遍历、相交测试时都可以将SIMD并行指令应用在执行过程, 加速数据处理速度。

(2)基于优化算子的SIMD并行算法

两个碰撞的模型是两个特征集合, 在解空间里就是两个模型的坐标点, 判断两物体是否发生碰撞就是判断两个物体间是否有一特征对间的距离是否达到碰撞的条件。如果将每个特征集合做成一个蚁群, 就可以应用蚁群算法, 在蚁群算法中应用SIMD并行技术。

对于多种群的蚁群算法, 本文提出了一种新的可以避免过早局部收敛的算法, 使用了优化算子。算法开始执行时, 多种群蚁群都处于初始化状态, 在SIMD下并行执行, 如果某个子群陷入局部最优解, 利用信息素优化算子, 重新初始化这个子种群, 同时给出了该算法的SIMD并行实现过程。把这一算法应用到碰撞检测上, 采用了文献[10]的基于前线分解的方法。采用多进程、多线程的并行方式, 对碰撞检测任务进行细粒度分解, 对每个子任务使用负载均衡策略分配到多核处理器的各个处理核心上并行执行。

基于优化算子的并行算法具体实现过程:

Optimization Operator Collision Detection(M_i, M_j)

(1)输入空间解集 M={M₁, M₂, …, M_n}, 其中

M为蚁群, ∀ M_i∈ M为子群。

(2)输出∀ M_i∈ M, ∀ M_j∈ M, M_i ⋂i=1nM_j=∅或M_i ⋂i=1nM_j≠ ∅。其中

M_i ⋂i=1nM_j=∅为存在最优路径, 有碰撞发生; M_i ⋂i=1nM_j≠ ∅为不存在最优路径, 没有碰撞发生。

(3)初始化M及∀ M_i∈ M子群; 置任意两子群M_i, M_j的检测标志M_if=0, M_jf=0。

构造预检测的层次包围盒BVH:

前线节点集FV={fv₁, fv₂, …, fv_n}

初始化堆栈LIVESM_i=∅,

LIVESM_j=∅;

初始化碰撞检测标志Collision

flag=FALSE。

(4)如果蚁群M=∅, 表示所有子群都检测完成, 则算法结束, 转到(7); 否则在M中删除M_if=1; M_jf=1的子群; 采用SIMD并行指令并行执行∀ M_i∈ M, ∀ M_j∈ M且M_if=0, M_jf=0任意两子群M_i, M_j的相交检测。

(5)采用SIMD并行多进程、多线程技术更新FV={fv₁, fv₂, …, fv_n}; 更新检测模型的顶点坐标; 更新层次包围盒BVH。

(6)判断是否存在最优解M_i ⋂i=1nM_j=∅; 如果M_i ⋂i=1nM_j=∅, 存在最优路径, 有碰撞发生, Collision flag=TURE。

将检测到碰撞的两个子群压入堆栈, Push M_i, M_j to LIVESM_i, LIVESM_j。

利用优化算子重新初始化子群M_i, M_j, 使M_if=1, M_jf=1。转到(4)。

(7)输出所有M_i ⋂i=1nM_j=∅的最优路径, 即M中所有发生碰撞的解集。

如果(LIVESM_i≠ ∅, LIVESM_j≠ ∅)

Pop LIVESM_i, LIVESM_j。

算法结束。