基于强跟踪卡尔曼滤波的陀螺信号处理

引用本文

朱枫, 张葆, 李贤涛, 王正玺, 张士涛. 基于强跟踪卡尔曼滤波的陀螺信号处理[J].吉林大学学报（工学版）, 2017,47(6): 1868-1875
ZHU Feng, ZHANG Bao, LI Xian-tao, WANG Zheng-xi, ZHANG Shi-tao. Gyro signal processing based on strong tracking Kalman filter[J]. Journal of Jilin University Engineering and Technology Edition, 2017,47(6): 1868-1875 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201706027
Permissions

基于强跟踪卡尔曼滤波的陀螺信号处理

朱枫^1,^2,³, 张葆^1,², 李贤涛^1,², 王正玺^1,^2,³, 张士涛^1,^2,³

1.中国科学院长春光学精密机械与物理研究所,长春 130033

2.中国科学院航空光学成像与测量重点实验室,长春 130033

3.中国科学院大学,北京 100049

通讯作者：张葆(1966-),男,研究员,博士.研究方向:航空光电成像技术.E-mail:zcleresky@vip.sina.com

作者简介:朱枫(1992-),女,博士研究生.研究方向:航空光电稳定平台视轴稳定技术.E-mail:zf0109@126.com

基金:“863”国家高技术研究发展计划重点项目(2013AA122102)

摘要

针对陀螺传感器测量精度低,严重影响航空光电稳定平台视轴稳定精度的问题,设计了强跟踪卡尔曼滤波器。根据时间序列分析法的基本原理,对经过预处理的陀螺原始量测数据进行AR模型建模,根据该AR模型采用状态空间法设计卡尔曼滤波器,同时为了增强系统的鲁棒性,引入强跟踪算法对卡尔曼滤波中的状态预测方差进行实时调整,构造了强跟踪卡尔曼滤波器。阐述了该算法的理论、原理,并且在某型航空光电稳定平台上进行试验验证。试验结果表明:强跟踪卡尔曼滤波器输出信号的方差减少了44.1%,分散程度降低,同时,相较于巴特沃斯滤波器,最大超调量减少13%,上升时间缩短了3 ms,调整时间缩短了37.5 ms,使平台具有良好的动态性能。研究表明,强跟踪卡尔曼滤波器可以提高航空光电稳定平台的精度,有较高的实用价值。

关键词: 自动控制技术; 视轴稳定精度; 强跟踪卡尔曼滤波; 陀螺传感器

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2017)06-1868-08

Gyro signal processing based on strong tracking Kalman filter

ZHU Feng^1,^2,³, ZHANG Bao^1,², LI Xian-tao^1,², WANG Zheng-xi^1,^2,³, ZHANG Shi-tao^1,^2,³

1.Changchun Institute of Optics, Fine Mechanics and Physics, Chinese Academy of Sciences, Changchun 130033, China

2.Key Laboratory of Airborne Optical Imaging and Measurement, Chinese Academy of Sciences,Changchun 130033,China

3.University of Chinese Academy of Sciences, Beijing 100049, China

Abstract

To overcome the problem that the low measuring precision of the gyroscope leads to degradation of Line of Sight (LOS) stabilization accuracy of photoelectric stabilized platform for aviation, a strong tracking Kalman filter was designed. According to the principle of the time sequence analysis from the random series, Autoregressive method (AR) was adopted to model the preprocessed data measured by the gyroscope. The state-space method was used to design the Kalman filter. In the meantime, in order to increase the control system's robustness, the strong tracking algorithm was introduced to correct the variance of state prediction in real time to construct the strong tracking Kalman filter. The theory and principle of the algorithm were described and applied to the photoelectric stabilized platform for aviation. The results show that the variance of signal was reduced by 44.1% after filtering using the strong tracking Kalman filter, and the dispersion was apparently reduced. At the same time, comparing with the Butterworth filter, the strong tracking Kalman filter shortens the overshoot by 13%, cut down the rise time by 3 ms, shortens the regulation time by 37.5 ms, keeps the platform in good dynamic properties. The study indicated that the strong tracking Kalman filter has strong application value.

Keyword: automatic control technology; LOS stabilization accuracy; strong tracking Kalman filter; gyroscope

Show Figures

0 引言

高精度的航空光电稳定平台是由多级框架、光电红外系统以及激光瞄准系统组成的综合航空遥感器^[1], 其主要作用是隔离载体的扰动, 使航空光电稳定平台的视轴能够迅速、平稳地跟踪和侦察靶标, 实现激光功率即使通过长距离传输后仍能集中在靶标上^[2]。航空光电稳定平台具有较好的机动性、鲁棒性以及实时性等特点, 从而被广泛应用于地质测绘、军事侦察、军事打击引导等多个领域。

陀螺是航空光电稳定平台伺服控制系统的核心敏感传感器^[3], 伺服控制系统利用陀螺传感器敏感平台的角速度信号, 进而驱动电机反向运动补偿该角速度, 从而保持惯性空间的稳定。因此, 陀螺传感器的测量精度直接影响航空光电稳定平台的视轴稳定精度。但是受陀螺传感器自身、半导体热噪声、电磁干扰等影响^[4], 使得陀螺的输出数据不可避免地含有随机噪声。为保证平台对目标的精准追踪, 需要对陀螺信号进行滤波处理, 进而抑制随机噪声对视轴稳定的不利影响。目前工程上多应用二阶或高阶巴特沃斯滤波器, 这种方法虽然可以在高频信号方面有效地抑制随机噪声, 但是会在陀螺的低频信号区域产生相位延迟, 影响陀螺信号的准确性和实时性。

1960年卡尔曼滤波理论^[5]以其具有实时递推、存储量小和简单易行的特点被广泛地应用于各大领域。标准卡尔曼滤波算法假设系统为随机线性系统, 需要精确的系统模型参数。但是, 在实际的工程应用中, 对系统模型无法精确测量, 存在一定范围的摄动, 这时应用标准卡尔曼滤波器会导致滤波性能变坏甚至发散^[6]。为了提高算法对系统误差的鲁棒性, 本文采用强跟踪算法^[7]对卡尔曼滤波算法中的状态预测方差进行实时修正, 提高系统在有不确定性情况下对状态估计的精度, 进而提高传感器的测量精度, 增强控制系统的性能。

本文从工程应用的角度出发, 利用时间序列分析法对陀螺信号进行建模分析, 根据状态空间法为系统建立状态方程和量测方程。在标准卡尔曼滤波的基础上, 引入强跟踪因子, 构建了强跟踪卡尔曼滤波器, 对随机噪声进行滤波处理, 从而提高了视轴稳定精度, 优化了控制系统的性能。

1 陀螺噪声分析

陀螺噪声随机过程是各态历经的随机过程, 因此要对噪声特性进行分析, 必须对其进行快速傅里叶变换得到其功率谱, 随后根据噪声频率域的分布情况对输入信号进行滤波。

试验所选用的陀螺型号为qrs14, 具体形态如图1所示。

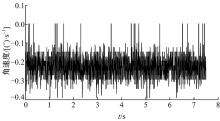
	Figure Option View Download New Window
	图1 qrs14陀螺传感器Fig.1 Gyroscope of qrs14

在恒温条件下, 对陀螺的静态角速率输出进行采集, 外部平台输入量为零, 此时陀螺的期望输出值为零, 所得数据即为该陀螺的零位噪声, 如图2所示。

	Figure Option View Download New Window
	图2 陀螺的零位噪声Fig.2 Zero noise of gyroscope

通过对多组压电陀螺零位噪声进行分析, 去掉对应陀螺偏置的直流分量后, 对该噪声序列进行快速傅里叶变换(FFT)得到功率谱密度, 如图3所示。

	Figure Option View Download New Window
	图3 零位噪声的功率谱Fig.3 Power spectrum of zero noise

分析功率谱可知, 陀螺噪声功率谱密度值在低频部分最为显著, 如果采用一阶巴特沃斯滤波或者滑动平均法滤波, 只能抑制噪声的高频部分, 对陀螺噪声不能起到较好的消除作用。而若采用二阶或更高阶巴特沃斯滤波器, 虽然去噪效果很好, 但是会引起相位延迟, 影响信号的实时性和准确性, 进而影响伺服系统的控制性能。

2 时间序列分析法

2.1 基本原理

时间序列分析^[8]是对有序的随机序列进行分析、处理, 根据系统的输出数据推测系统内部时性和外部的影响, 同时预测系统的未来状况。时间序列信号模型是一个线性模型, 具有连续功率谱的特性。许多平稳随机序列都可以看成是由典型噪声源激励一个线性系统产生的, 这种噪声源一般是白噪声序列。在实际应用中, 根据陀螺随机漂移特性对输出信号进行建模, 利用白噪声驱动下自回归(AR)模型的线性组合, 对陀螺输出的随机信号进行拟合。通过使用不同阶次的线性模型, 以及对信号的总体考虑, 在时域上对陀螺信号进行建模, 其建模结果可为卡尔曼滤波中状态矩阵的参数设置提供参考。

时间序列法的基本模型为自回归滑动平均模型, 即ARMA(p, q)模型^[9], 其一般形式为:

$\begin{matrix} \begin{matrix} x (k) = a_{1} x (k - 1) + \dots + a_{p} x (k - p) + w (k) \\ - b_{1} w (k - 1) + \dots + b_{q} w (k - q) (1) \end{matrix} \end{matrix}$

式中: $\begin{matrix} p \end{matrix}$ 为自回归AR模型的阶数; $\begin{matrix} q \end{matrix}$ 为滑动平均MA模型的阶数; $\begin{matrix} x (k) \end{matrix}$ 为时间序列信号; $\begin{matrix} w (k) \end{matrix}$ 为零均值、方差为 $\begin{matrix} σ_{w}^{2} \end{matrix}$ 的白噪声序列; $\begin{matrix} a_{1}, a_{2}, \dots, a_{p} \end{matrix}$ 为自回归系数; $\begin{matrix} b_{1}, b_{2}, \dots, b_{p} \end{matrix}$ 为滑动平均系数。

当 $\begin{matrix} q = 0 \end{matrix}$ 时, 方程(1)退化为 $\begin{matrix} p \end{matrix}$ 阶AR模型, 即:

$\begin{matrix} x (k) = a_{1} x (k - 1) + \dots + a_{p} x (k - p) + w (k) (2) \end{matrix}$

当 $\begin{matrix} p = 0 \end{matrix}$ 时, 方程(1)退化为 $\begin{matrix} q \end{matrix}$ 阶MA模型, 即:

$\begin{matrix} x (k) = w (k) - b_{1} w (k - 1) - \dots - b_{q} w (k - q) (3) \end{matrix}$

2.2 数据的预处理

由于时间序列法要求数据为零均值平稳随机序列, 所以需要对采集的零位噪声进行数据预处理^[10]。

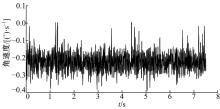
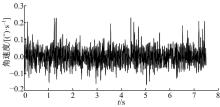
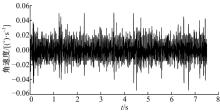
首先对数据进行平滑处理, 去除明显异常的野值, 如图4所示。再去除趋势项, 使数据的均值为零, 如图5所示。最后, 为了保证数据的平稳性, 进行一阶差分处理, 如图6所示。

	Figure Option View Download New Window
	图4 平滑处理后的信号Fig.4 Signal after smoothing

	Figure Option View Download New Window
	图5 去除趋势项后的信号Fig.5 Signal after subtracting the mean value from data

	Figure Option View Download New Window
	图6 一阶差分的信号Fig.6 First order difference signal

处理后的数据可以根据时间序列分析法构建传感器的数学模型。

2.3 随机序列模型的选择

由于陀螺的模型阶次都比较低, 一般不超过二到三阶, 并且, 在实际应用工程应用中, ARMA模型的自回归阶数大于或等于滑动平均阶数^[11], 所以陀螺模型一般选为AR(1)、AR(2)、AR(3)、ARMA(1, 1)、ARMA(2, 1)。

对于随机序列模型阶次的选择通常采用FPE准则, 具体公式为:

$\begin{matrix} FPE = \frac{N + k}{N - k} {\hat{ρ}}_{k} (4) \end{matrix}$

式中: $\begin{matrix} {\hat{ρ}}_{k} 为 k \end{matrix}$ 阶模型的白噪声方差(预测误差方差)的估计值。

各模型参数及其FPE值如表1所示。

表1 模型参数及其FPE值 Table 1 Mathematic models’ parameters and values of FPE

参数	AR(1)	AR(2)	AR(3)	ARMA(1, 1)	ARMA(2, 1)
$\begin{matrix} a_{1} \end{matrix}$	0.8347	0.7629	0.8347	0.7853	0.0021
$\begin{matrix} a_{2} \end{matrix}$	-	0.0859	0.2847	-	0.7416
$\begin{matrix} a_{3} \end{matrix}$	-	-	-0.2605	-
$\begin{matrix} b_{1} \end{matrix}$	-	-	-	0.0578	-0.7416
FPE/10^-5	4.259	4.228	3.982	4.243	4.055

表1 模型参数及其FPE值 Table 1 Mathematic models’ parameters and values of FPE

通过对比表1中各模型的FPE值可以看出, 5个模型的FPE值都很小并且相差不大。考虑到后续计算的复杂程度以及算法的运行效率, 本文选用AR(1)模型构建陀螺方程:

$\begin{matrix} x_{k} = 0.8347 x_{k - 1} + w_{k} (5) \end{matrix}$

此方程可为卡尔曼滤波的状态方程的参数设定提供参考。

3 强跟踪卡尔曼滤波器的设计

3.1 卡尔曼滤波器的设计

根据式(5)构造卡尔曼滤波系统的状态方程和观测方程^[12]:

$\begin{matrix} \begin{matrix} X_{k} = φ_{k, k - 1} X_{k - 1} + Γ_{k, k - 1} W_{k - 1} (6) \\ Z_{k} = H_{k} X_{k} + V_{k} (7) \end{matrix} \end{matrix}$

式中: $\begin{matrix} X_{k} \end{matrix}$ 为系统的状态序列; $\begin{matrix} Z_{k} \end{matrix}$ 为系统的观测序列; $\begin{matrix} W_{k - 1} \end{matrix}$ 为系统的过程噪声; $\begin{matrix} V_{k} \end{matrix}$ 为系统的观测噪声; $\begin{matrix} φ_{k, k - 1} \end{matrix}$ 为状态转移矩阵; $\begin{matrix} Γ_{k, k - 1} \end{matrix}$ 为噪声输入矩阵; $\begin{matrix} H_{k} \end{matrix}$ 为观测矩阵。

关于系统过程噪声和观测噪声的统计特性, 假定如下:

$\begin{matrix} \{\begin{matrix} E [W_{k}] = 0, E [W_{k} {W^{T}}_{j}] = Q_{k} δ_{kj} \\ E [V_{k}] = 0, E [V_{k} {V^{T}}_{j}] = R_{k} δ_{kj} \\ E [W_{k} {V^{T}}_{j}] = 0 \end{matrix} (8) \end{matrix}$

式中: $\begin{matrix} Q_{k} \end{matrix}$ 为系统过程噪声 $\begin{matrix} W_{k} \end{matrix}$ 的对称非负定方差矩阵; $\begin{matrix} R_{k} \end{matrix}$ 为观测噪声 $\begin{matrix} V_{k} \end{matrix}$ 的对称正定方差矩阵; $\begin{matrix} δ_{kj} \end{matrix}$ 为Kronecker-δ 函数。

卡尔曼滤波递推公式如下所示。

状态一步预测:

$\begin{matrix} {\hat{X}}_{k, k - 1} = φ_{k, k - 1} {\hat{X}}_{k - 1} (9) \end{matrix}$

一步预测误差方差矩阵为:

$\begin{matrix} P_{k, k - 1} = φ_{k, k - 1} P_{k - 1} {φ^{T}}_{k, k - 1} + Γ_{k, k - 1} Q_{k - 1} {Γ^{T}}_{k, k - 1} (10) \end{matrix}$

滤波增益矩阵为:

$\begin{matrix} K_{k} = P_{k, k - 1} {H^{T}}_{k} [H_{k} P_{k, k - 1} {H^{T}}_{k} + R_{k}]^{- 1} (11) \end{matrix}$

估计误差方差矩阵为:

$\begin{matrix} \begin{matrix} P_{k - 1} = [1 - K_{k} H_{k}] P_{k, k - 1} [1- \\ K_{k} H K_{k}]^{- 1} + K_{k} R_{k} {K^{T}}_{k} (12) \end{matrix} \end{matrix}$

状态估计为:

$\begin{matrix} {\hat{X}}_{k} = {\hat{X}}_{k, k - 1} + K_{k} [Z_{k} - H_{k} {\hat{X}}_{k, k - 1}] (13) \end{matrix}$

3.2 强跟踪滤波器的设计

标准卡尔曼滤波需要明确系统模型, 但是由于系统模型的简化、噪声统计特性不准确以及实际系统的参数发生变动等原因, 使得系统模型存在大量的不确定性, 即所建立的系统模型与其所描述的系统不匹配。

针对上述原因, 为了提高系统的鲁棒性, 采用强跟踪滤波算法, 利用衰减记忆滤波思想, 将渐消因子引入状态预测误差协方差阵^[13], 从而实时调整滤波增益矩阵, 强迫滤波残差序列保持相互正交, 使得强跟踪滤波器保持对系统实际状态的跟踪^{[14, 15]}。

利用时变渐消因子对过去的数据进行渐消, 减弱陈旧数据对当前滤波值的影响, 通过实时调整预测误差的协方差矩阵以及相应的增益矩阵来增强滤波器对状态突变的跟踪能力。在标准卡尔曼滤波算法的基础上按照强跟踪滤波算法在计算状态预测方差 $\begin{matrix} P_{k, k - 1} \end{matrix}$ 时引入一个渐消因子便是强跟踪卡尔曼滤波算法^[16]:

$\begin{matrix} P_{k, k - 1} = λ_{k - 1} φ_{k, k - 1} P_{k - 1} φ_{k, k - 1} + Q_{k - 1} (14) \end{matrix}$

式中: $\begin{matrix} λ_{k} \geq 1 \end{matrix}$ 为自适应渐消因子, 可由下面算法^[17]确定:

$λ_{k} = \{\begin{matrix} λ_{0, k}, λ_{0, k} \geq 1 \\ 1, λ_{0, k} < 1 \end{matrix} (15)$

$λ_{0, k} = \frac{Tr (N_{k})}{Tr (M_{k})} (16)$

$N_{k} = V_{k} - Q_{k - 1} - lR (17)$

$\tilde{y} (k) = Z_{k} - {\hat{X}}_{k} (18)$

$V_{k} = \{\begin{matrix} {\tilde{y}}^{2} (1), k = 1 \\ \frac{ρ V_{k} + {\tilde{y}}^{2} (k)}{1 + ρ}, k \geq 2 \end{matrix} (19)$

$M_{k} = φ_{k, k - 1}^{2} {\hat{P}}_{k - 1} (20)$

式中: $\begin{matrix} 0 < ρ \leq 1 \end{matrix}$ 为遗忘因子, $\begin{matrix} l \geq 1 \end{matrix}$ 为弱化因子, 取值根据试验具体调整。

4 试验验证

为了验证在实际工程中跟踪微分器的滤波效果, 在某型航空光电稳定平台上进行试验。试验环境如图7所示, 为某型航空光电稳定平台和用于模拟飞机飞行中姿态变化的模拟转台。

	Figure Option View Download New Window
	图7 航空光电稳定平台和飞行模拟转台Fig.7 Aerial photoelectrical stabilized platform and swing table

4.1 滤波器的带宽设计

伺服系统速度环的带宽为15 Hz, 为了保持平台控制系统的稳定性, 滤波器的带宽应大于速度环带宽, 从而保持一定的相位裕度和幅值裕度。

图8为二阶巴特沃斯滤波器和强跟踪卡尔曼滤波器的频率响应Bode图。

	Figure Option View Download New Window
	图8 巴特沃斯滤波器和强跟踪卡尔曼滤波器的Bode图Fig.8 Bode of Butterworth filter and strong tracking Kalman filter

从图8中可以看出, 两个滤波器均在300 rad前后开始幅值衰减, 但是强跟踪卡尔曼滤波器没有带来相位的损失, 明显优于二阶巴特沃斯滤波器, 能够满足控制系统对滤波器的带宽要求。

4.2 零位噪声的抑制

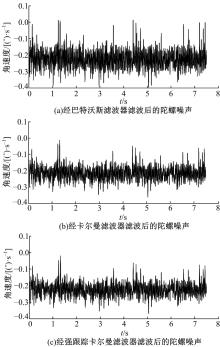
将采集到的陀螺零位噪声数据分别用二阶巴特沃斯滤波器、卡尔曼滤波器和强跟踪卡尔曼滤波器进行滤波处理, 如图9所示。滤波前、后的信号均值和方差如表2所示。

从图9中可以看出, 经过强跟踪卡尔曼滤波器, 陀螺零位输出信号的方差减少了44.1%, 分散程度显著降低, 可见强跟踪卡尔曼滤波器对于陀螺的零位噪声抑制效果最好。

	Figure Option View Download New Window
	图9 三种滤波方法的阶跃响应曲线对比Fig.9 Contrast of three kinds of filter’ s step response of platform

表2 陀螺信号的均值和方差 Table 2 Mean value and variance deviation of Gyro signal

4.3 恒定速率的阶跃响应试验

在平台中给定恒定的速度输入值为10° /s, 分别在二阶巴特沃斯滤波器、卡尔曼滤波器、强跟踪卡尔曼滤波器下进行阶跃响应试验, 观察系统的动态性能, 曲线如图10所示。

	Figure Option View Download New Window
	图10 三种滤波方法的阶跃响应曲线对比Fig.10 Contrast of three kinds of filter’ s step response of platform

通过观察3种阶跃响应曲线可知, 强跟踪卡尔曼滤波器控制下的伺服系统的动态特性得到优化, 波动小、平稳性好, 最大超调量减少13%, 上升时间缩短了3 ms, 调整时间缩短了37.5 ms。这充分说明了在强跟踪卡尔曼滤波器控制下的系统响应速度快、调节时间短, 有效提升了控制系统的动态性能。

4.4 摇摆试验

设置平台的转动速度为一个正弦信号, 幅值为15° /s, 频率为10 Hz。分别观察在二阶巴特沃斯滤波器和强跟踪卡尔曼滤波器控制下的系统输出曲线, 结果如图11所示。

	Figure Option View Download New Window
	图11 两种滤波方法的正弦曲线对比Fig.11 Contrast of two kinds of filter’ s sine wave

从图11可以看出:相较于原始陀螺信号, 两个滤波器都有很好的滤波效果。但是二阶巴特沃斯滤波器的相位略有滞后, 而强跟踪卡尔曼滤波器很好地保证了信号的实时性, 几乎没有相位损失, 良好地保持了系统的控制性能。

4.5 鲁棒性测试

在同样的试验环境下, 针对同一个陀螺传感器, 验证对系统的模型参数估计存在误差时系统的鲁棒性。将系统模型参数分别增大和减小10%, 即状态参数分别为0.9182和0.7512。在这两种情况下分别用卡尔曼滤波器和强跟踪卡尔曼滤波器对陀螺传感器进行滤波。表3为状态参数为0.9182时卡尔曼滤波器和强跟踪卡尔曼滤波器对陀螺的零位噪声的滤波效果。表4为状态参数为0.7512时卡尔曼滤波器和强跟踪卡尔曼滤波器对陀螺的零位噪声的滤波效果。

表3 参数为0.9182时信号的均值和方差 Table 3 Mean value and Variance deviation of Gyro signal when parameter increased to 0.9182

表4 参数为0.7512时信号的均值和方差 Table 4 Mean value and Variance deviation of Gyro signal when parameter decreased to 0.7512

通过观察表3和表4中数据可以看出:当系统的模型参数存在一定范围的摄动, 带有误差时, 强跟踪卡尔曼滤波器依旧可以保持对噪声较强的抑制能力, 提高传感器信号的精度, 使系统具有较强的鲁棒性。

5 结束语

针对陀螺传感器测量精度低的实际工程问题, 本文提出了强跟踪卡尔曼滤波器, 摒弃了传统的巴特沃斯滤波器, 以改善相位延迟问题。利用时间序列法为传感器构建状态方程, 在传统卡尔曼滤波理论的基础上, 引入了强跟踪算法, 构建了强跟踪卡尔曼滤波器。试验结果表明, 对比滤波前、后的信号方差, 经过强跟踪卡尔曼滤波器输出的信号方差降低了44.1%。对于阶跃响应, 系统的最大超调量减少了13%, 调整时间缩短了37.5 ms, 显著地提升了平台的动态响应性能。当系统模型参数存在一定范围的摄动时, 强跟踪卡尔曼滤波器保持了信号的高精度, 同时还具备标准卡尔曼滤波器所欠缺的鲁棒性。综上所述, 本文所设计的强跟踪卡尔曼滤波器, 有较好的实用性和较高的工程应用价值, 具有广阔的应用前景。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	魏伟, 戴明, 李嘉全, 等. 航空光电稳定平台的自抗扰控制系统[J]. 光学精密工程, 2015, 23(8): 2296-2305. Wei Wei, Dai Ming, Li Jia-quan, et al. ADRC control system for airborne opto-electronic platform[J]. Optics and Precision Engineering, 2015, 23(8): 2296-2305. [本文引用:1]
[2]	李贤涛, 张葆, 沈宏海. 基于自抗扰控制技术提高航空光电稳定平台的扰动隔离度[J]. 光学精密工程, 2014, 22(8): 2223-2231. Li Xian-tao, Zhang Bao, Shen Hong-hai. Improvement of isolation degree of aerial photoelectrical stabilized platform based on ADRC[J]. Optics and Precision Engineering, 2014, 22(8): 2223-2231. [本文引用:1]
[3]	成宇翔, 张卫平, 陈文元, 等. MEMS微陀螺仪研究进展[J]. 微纳电子技术, 2011, 48(5): 277-285. Cheng Yu-xiang, Zhang Wei-ping, Chen Wen-yuan, et al. Research development of MEMS micro-gyroscopes[J]. Micronanoelectronic Technology, 2011, 48(5): 277-285. [本文引用:1]
[4]	孙树红, 赵长海, 万秋华, 等. 小型光电编码器自动检测系统[J]. 中国光学, 2013, 6(4): 600-606. Sun Shu-hong, Zhao Chang-hai, Wan Qiu-hua, et al. Automatic detection system for miniature photoelectrical encoder[J]. Chinese Optics, 2013, 6(4): 600-606. [本文引用:1]
[5]	Kalman R E. A new approach to linear filtering and prediction problems[J]. Journal of Basic Engineering Transactions, 1960: 82(Series D): 35-45. [本文引用:1]
[6]	Kirkko-Jaakkola M, Collin J, Takala J. Bias Prediction for MEMS Gyroscopes[J]. IEEE Sensors Journal, 2012, 12(6): 2157-2163. [本文引用:1]
[7]	Park S, Horowitz R. Adaptive control for the conventional mode of operation of MEMS gyroscopes[J]. Journal of Microelectromechanical Systems, 2003, 12(1): 101-108. [本文引用:1]
[8]	李贤涛, 张葆, 赵春蕾, 等. 基于自适应的自抗扰控制技术提高扰动隔离度[J]. 吉林大学学报: 工学版, 2015, 45(1): 202-208. Li Xian-tao, Zhang Bao, Zhao Chun-lei, et al. Improve isolation degree based on adaptive active disturbance rejection controller[J]. Journal of Jilin University (Engineering and Technology Edition), 2015, 45(1): 202-208. [本文引用:1]
[9]	魏伟, 戴明, 李嘉全, 等. 基于重复-自抗扰控制的航空光电稳定平台控制系统设计[J]. 吉林大学学报: 工学版, 2015, 45(6): 1924-1932. Wei Wei, Dai Ming, Li Jia-quan, et al. Design of airborne opto-electric platform control system based on ADRC and repetitive control theory[J]. Journal of Jilin University(Engineering and Technology Edition), 2015, 45(6): 1924-1932. [本文引用:1]
[10]	韩京清. 自抗扰控制技术[J]. 前沿科学, 2007(1): 24-31. Han Jing-qing. Active disturbance rejection control technique[J]. Frontier Science, 2007(1): 24-31. [本文引用:1]
[11]	丛爽, 孙光立, 邓科, 等. 陀螺稳定平台的自抗扰及其滤波控制[J]. 光学精密工程, 2016, 24(1): 169-177. Cong Shuang, Sun Guang-li, Deng Ke, et al. Active disturbance rejection and filter control of gyro-stabilized platform[J]. Optics and Precision Engineering, 2016, 24(1): 169-177. [本文引用:1]
[12]	钱华明, 夏全喜, 阙兴涛, 等. 基于Kalman滤波的MEMS陀螺仪滤波算法[J]. 哈尔滨工程大学学报, 2010, 31(9): 1217-1221. Qian Hua-ming, Xia Quan-xi, Que Xing-tao, et al. Algorithm for a MEMS gyroscope based on Kalman filter[J]. Journal of Harbin Engineering University, 2010, 31(9): 1217-1221. [本文引用:1]
[13]	李慧, 吴军辉, 朱霞, 等. 速率陀螺式激光导引头稳定跟踪原理分析与仿真[J]. 红外与激光工程, 2011, 40(7): 1337-1341. Li Hui, Wu Jun-Hui, Zhu Xia, et al. Analysis and tracking principle for rate gyroscope laser seeker[J]. Infrared and Laser Engineering, 2011, 40(7): 1337-1341. [本文引用:1]
[14]	骆荣剑, 李颖, 钱广华, 等. 机动目标跟踪中一种改进的自适应卡尔曼滤波算法[J]. 重庆邮电大学学报: 自然科学版, 2015, 27(1): 31-36. Luo Rong-jian, Li Ying, Qian Guang-hua, et al. Improved maneuvering target tracking adaptive Kalman filter algorithm[J]. Chongqing University of Posts and Telecommunications Journal(Natural Science Edition), 2015, 27(1): 31-36. [本文引用:1]
[15]	李刚, 蔡成林, 李思敏, 等. 抗差与自适应组合的卡尔曼滤波算法在动态导航中的研究[J]. 重庆邮电大学学报: 自然科学版, 2015, 27(1): 37-43. Li Gang, Cai Cheng-lin, Li Si-min, et al. Robust adaptive Kalman filter in kinematic positioning[J]. Chongqing University of Posts and Telecommunications Journal(Natural Science Edition), 2015, 27(1): 37-43. [本文引用:1]
[16]	蒙涛, 王昊, 李辉, 等. MEMS陀螺误差建模与滤波方法[J]. 系统工程与电子技术, 2009, 31(8): 1944-1948. Meng Tao, Wang Hao, Li Hui, et al. Error modeling and filtering method for MEMS gyroscope[J]. Systems Engineering and Electronics, 2009, 31(8): 1944-1948. [本文引用:1]
[17]	宋康宁, 丛爽, 邓科, 等. 自适应强跟踪卡尔曼滤波在陀螺稳定平台中的应用[J]. 中国科学技术大学学报, 2015, 45(1): 17-22. Song Kang-ning, Cong Shuang, Deng Ke, et al. Application of adaptive strong tracking Kalman filter to gyro-stabilized platform[J]. Journal of University of Science and Technology of China, 2015, 45(1): 17-22. [本文引用:1]

2015

0.0

. 2015, 23(8):2296-2305 DOI:doi:10.3788/OPE.20152308.2296

ADRC control system for airborne opto-electronic platform

航空光电稳定平台的自抗扰控制系统

Wei Wei , Dai Ming , Li Jia-quan

魏伟, 戴明, 李嘉全

摘　要：对航空光电稳定平台模型进行分析并利用电流环简化了平台模型。阐述了影响平台稳定性的扰动及抑制扰动的方法,提出一种基于预报修正的自抗扰控制系统。首先,提出了一种预报修正方法,采用＂先预报,后修正＂的方法来减小扰动观测值的滞后和超调;然后,设计了基于二阶扩张状态观测器的自抗扰控制系统,对扰动进行线性化动态补偿;最后,在振动平台上对系统进行了速度稳定实验、目标跟踪实验和鲁棒性分析。结果表明,与经典的平方滞后超前控制方法相比,本文设计的控制方法对扰动的隔离度至少提高了5.88dB。另外,设计的系统具有很强的鲁棒性,在系统参数改变±15%的范围内,仍得到很好的控制效果。由于所设计的控制系统具有很强的实用性和鲁棒性,在工程实际应用中提高了航空光电稳定平台的抗扰动性能。

... 0 引言高精度的航空光电稳定平台是由多级框架、光电红外系统以及激光瞄准系统组成的综合航空遥感器^[1],其主要作用是隔离载体的扰动,使航空光电稳定平台的视轴能够迅速、平稳地跟踪和侦察靶标,实现激光功率即使通过长距离传输后仍能集中在靶标上^[2] ...

2014

0.0

. 2014, 22(8):2223-2231

Improvement of isolation degree of aerial photoelectrical stabilized platform based on ADRC

基于自抗扰控制技术提高航空光电稳定平台的扰动隔离度

Li Xian-tao , Zhang Bao , Shen Hong-hai.

李贤涛, 张葆, 沈宏海

2011

0.0

. 2011, 48(5):277-285 DOI:doi:10.3969/j.issn.1671-4776.2011.05.001

Research development of MEMS micro-gyroscopes

MEMS微陀螺仪研究进展

Cheng Yu-xiang , Zhang Wei-ping , Chen Wen-yuan

成宇翔, 张卫平, 陈文元

摘　要：回顾了MEMS微陀螺仪的研究进展,简单介绍了MEMS微陀螺仪的市场应用。微陀螺仪是 MEMS器件中非常重要的一类器件。它的运用已经从单纯的航空领域逐渐转向汽车、消费电子行业等低端市场,这意味着微陀螺仪除了传统意义上的高精度高稳定性的要求,也可以向低精度商品化发展。传统的振动式陀螺,由于原理的局限性和加工技术的限制,很难达到战术级和惯性级的要求。导航级集成微陀螺（NGIMG）项目建议使用其他途径,以减少器件的可移动部件和降低工艺难度,从而提高其精度和抗干扰能力。各种设计方法近年来层出不穷,其中悬浮转子式微陀螺是目前精度最高的陀螺仪,微集成光学式陀螺也将在未来一段时间拥有巨大的研究潜力和发展空间。

... 陀螺是航空光电稳定平台伺服控制系统的核心敏感传感器^[3],伺服控制系统利用陀螺传感器敏感平台的角速度信号,进而驱动电机反向运动补偿该角速度,从而保持惯性空间的稳定 ...

2013

0.0

. 2013, 6(4):600-606 DOI:doi:10.3788/CO.20130604.0600

Automatic detection system for miniature photoelectrical encoder

小型光电编码器自动检测系统

Sun Shu-hong , Zhao Chang-hai , Wan Qiu-hua

孙树红, 赵长海, 万秋华

An automatic detection system was designed to quickly and accurately detect the precision of a miniature photoelectric encoder. A 21 bit high precision photoelectric encoder was used as the reference to detect the low precision miniature photoelectric encoder. The control system was taken to rotate the encoder first, and the difference of the high precision encoder and the miniature encoder was the error of the miniature encoder. After the testing was completed, the errors of encoder were transmitted to the host computer through the USB interface to save and to perform an in-depth analysis. A 15-bit encoder was detected by using the system, the mean square deviation of the encoder is 29.1 s, however the mean square deviation of the encoder is 28.5 s when the detection is done by the traditional methods. Obtained results meet the accuracy requirements.

设计了小型光电编码器自动检测系统,用于准确快速地检测小型光电轴角编码器的误差。采用21位高精度光电编码器作为角度基准来检测低精度的小型光电编码器。用控制系统转动编码器,此时高精度编码器与被检编码器之差即为小型编码器在该位置的误差。检测完毕,根据需要将编码器的误差通过USB接口传输给上位机保存并进行深度分析。采用该系统检测某型号的15位编码器,得到的均方差为29.1″,而传统方法检测的误差均方差为28.5″,表明设计的检测系统满足检测精度要求。

... 但是受陀螺传感器自身、半导体热噪声、电磁干扰等影响^[4],使得陀螺的输出数据不可避免地含有随机噪声 ...

1960

0.0

... 1960年卡尔曼滤波理论^[5]以其具有实时递推、存储量小和简单易行的特点被广泛地应用于各大领域 ...

2012

0.0

... 但是,在实际的工程应用中,对系统模型无法精确测量,存在一定范围的摄动,这时应用标准卡尔曼滤波器会导致滤波性能变坏甚至发散^[6] ...

2003

0.0

... 为了提高算法对系统误差的鲁棒性,本文采用强跟踪算法^[7]对卡尔曼滤波算法中的状态预测方差进行实时修正,提高系统在有不确定性情况下对状态估计的精度,进而提高传感器的测量精度,增强控制系统的性能 ...

2015

0.0

. 2015, 45(1):202-208

Improve isolation degree based on adaptive active disturbance rejection controller

基于自适应的自抗扰控制技术提高扰动隔离度

Li Xian-tao , Zhang Bao , Zhao Chun-lei

李贤涛, 张葆, 赵春蕾

... 1 基本原理时间序列分析^[8]是对有序的随机序列进行分析、处理,根据系统的输出数据推测系统内部时性和外部的影响,同时预测系统的未来状况 ...

2015

0.0

. 2015, 45(6):1924-1932 DOI:doi:10.13229/j.cnki.jdxbgxb201506028

Design of airborne opto-electric platform control system based on ADRC and repetitive control theory

基于重复-自抗扰控制的航空光电稳定平台控制系统设计

Wei Wei , Dai Ming , Li Jia-quan

魏伟, 戴明, 李嘉全

The airborne opto-electric stable platform model was analyzed and simplified to K/s with current loop. The disturbance to the platform stability and the disturbance rejection method were illustrated. The traditional square lag-lead compensation method, its strengths and weaknesses were introduced. The repetitive controller and Active Disturbance Rejection Controller (ADRC) were described. A repetitive controller and a two stage ADRC were designed, which were integrated into a new controller system taking the advantages of both. Speed stability experiment and target tracking experiment were carried out on a vibration platform. Results show that compared with conventional controllers, the proposed controller improves the disturbance isolation by 6.28 dB at least. On all accounts, the proposed control system has strong robustness, observably improves the disturbance isolation of the opto-electric platform and can provide guide for engineering applications.

分析了航空光电稳定平台模型并利用电流环使平台模型简化为K/s。阐述了影响平台稳定性的扰动以及抑制扰动的方法。介绍了平方滞后超前控制原理及其优缺点。根据重复控制器以及自抗扰控制器的优点,将它们组合搭建控制系统,并在振动平台上进行速度稳定和目标跟踪试验。结果表明:与传统的控制器相比,用本文控制方法得出的扰动隔离度至少提高了6.28 dB;所设计的系统在符合工程需求的范围内,具有很强的实用性和鲁棒性,对实际工程控制器设计具有一定的参考价值。

... 时间序列法的基本模型为自回归滑动平均模型,即ARMA(p,q)模型^[9],其一般形式为: ...

2007

0.0

... 2 数据的预处理由于时间序列法要求数据为零均值平稳随机序列,所以需要对采集的零位噪声进行数据预处理^[10] ...

2016

0.0

. 2016, 24(1):169-177

Active disturbance rejection and filter control of gyro-stabilized platform

陀螺稳定平台的自抗扰及其滤波控制

Cong Shuang , Sun Guang-li , Deng Ke

丛爽, 孙光立, 邓科

... 3 随机序列模型的选择由于陀螺的模型阶次都比较低,一般不超过二到三阶,并且,在实际应用工程应用中,ARMA模型的自回归阶数大于或等于滑动平均阶数^[11],所以陀螺模型一般选为AR(1)、AR(2)、AR(3)、ARMA(1,1)、ARMA(2,1) ...

2010

0.0

. 2010, 31(9):1217-1221 DOI:doi:10.3969/j.issn.1006-7043.2010.09.015

Algorithm for a MEMS gyroscope based on Kalman filter

基于Kalman滤波的MEMS陀螺仪滤波算法

Qian Hua-ming , Xia Quan-xi , Que Xing-tao

钱华明, 夏全喜, 阙兴涛

针对MEMS陀螺仪精度不高、随机噪声复杂的问题,研究了某MEMS陀螺仪的随机漂移模型.应用时间序列分析方法,采用AR(1)模型对经过预处理的MEMS陀螺仪测量数据噪声进行建模,进而基于该AR模型并采用状态扩增法设计Kalman滤波器.速率试验和摇摆试验仿真结果表明,在静态和恒定角速率条件下,采用该算法滤波后的MEMS陀螺仪的误差均值和标准差都比滤波前有了明显的降低.针对摇摆基座下该算法随摆动幅度的增大效果变差的问题,从提高采样率和选择自适应Kalman滤波2个方面对算法进行改进.仿真结果表明,2种方法都能改善滤波效果,然而考虑到系统采样频率和CPU计算速度的限制,自适应滤波有更高的实用性.

... 1 卡尔曼滤波器的设计根据式(5)构造卡尔曼滤波系统的状态方程和观测方程^[12]: ...

2011

0.0

. 2011, 40(7):1337-1341 DOI:doi:10.3969/j.issn.1007-2276.2011.07.030

Analysis and tracking principle for rate gyroscope laser seeker

速率陀螺式激光导引头稳定跟踪原理分析与仿真

Li Hui , Wu Jun-Hui , Zhu Xia

李慧, 吴军辉, 朱霞

摘　要：激光导引头是激光末制导武器（炮弹、炸弹和导弹）的核心部件,其性能优劣直接影响对目标的捕获、跟踪性能及命中精度,采用计算机仿真技术对激光导引头系统进行建模和仿真是一条有效评估其性能的途径。结合某速率陀螺稳定式激光导引头的结构特点,研究其空间稳定和跟踪的工作机理,并应用多体力学和空间飞行原理建立了该型导引头伺服系统的数学模型。仿真结果证明了导引头模型的正确性,全面体现了激光导引头的稳定与跟踪机理,为激光末制导武器全弹道仿真和激光干扰数学仿真系统的建立提供了模型支持。

... 针对上述原因,为了提高系统的鲁棒性,采用强跟踪滤波算法,利用衰减记忆滤波思想,将渐消因子引入状态预测误差协方差阵^[13],从而实时调整滤波增益矩阵,强迫滤波残差序列保持相互正交,使得强跟踪滤波器保持对系统实际状态的跟踪^[14,15] ...

2015

0.0

. 2015, 27(1):31-36 DOI:doi:10.3979/j.issn.1673-825X.2015.01.006

Improved maneuvering target tracking adaptive Kalman filter algorithm

机动目标跟踪中一种改进的自适应卡尔曼滤波算法

Luo Rong-jian , Li Ying , Qian Guang-hua

骆荣剑, 李颖, 钱广华

针对"当前"统计模型中预先设置机动频率和加速度极限值造成对目标跟踪精度不高的问题,提出一种新的参数自适应算法。该算法利用目标前后2个时刻的加速度均值代替"当前"统计模型中只利用前一时刻的加速度值作为当前时刻的加速度均值,推导出了机动频率自适应,再利用加速度方差与加速度变化量之间存在的正比线性关系,推导出了加速度方差自适应,避免了由于参数设置不合理而造成的跟踪误差。理论分析和仿真结果表明,改进算法有效提高了目标跟踪精度,仿真结果验证了改进算法的有效性。

2015

0.0

. 2015, 27(1):37-43 DOI:doi:10.3979/j.issn.1673-825X.2015.01.007

Robust adaptive Kalman filter in kinematic positioning

抗差与自适应组合的卡尔曼滤波算法在动态导航中的研究

Li Gang , Cai Cheng-lin , Li Si-min

李刚, 蔡成林, 李思敏

针对观测信息不充足时,无法使用现有的一些抗差自适应滤波的问题,提出一种组合抗差滤波和自适应滤波的方法.该方法利用基于m估计实现的抗差滤波和基于新息向量马氏距离平方服从卡方分布而构造的自适应滤波,同时采用2次对检验统计量进行判别的方法,可以在单个历元实现在标准卡尔曼滤波、自适应卡尔曼滤波和抗差卡尔曼滤波之间选择一种当前时刻的最优滤波,因此,采用该方法也能构成抗差自适应卡尔曼滤波.仿真结果表明,在观测信息不足且滤波模型出现异常时,该方法能有效控制动力学模型误差和观测异常对导航解的影响,使导航解更能反映导航系统的真实情况.

2009

0.0

. 2009, 31(8):1944-1948

Error modeling and filtering method for MEMS gyroscope

MEMS陀螺误差建模与滤波方法

Meng Tao , Wang Hao , Li Hui

蒙涛, 王昊, 李辉

... 在标准卡尔曼滤波算法的基础上按照强跟踪滤波算法在计算状态预测方差 Pk,k-1时引入一个渐消因子便是强跟踪卡尔曼滤波算法^[16]: ...

2015

0.0

. 2015, 45(1):17-22 DOI:doi:10.3969/j.issn.0253-2778.2015.01.003

Application of adaptive strong tracking Kalman filter to gyro-stabilized platform

自适应强跟踪卡尔曼滤波在陀螺稳定平台中的应用

Song Kang-ning , Cong Shuang , Deng Ke

宋康宁, 丛爽, 邓科

摘　要：考虑陀螺稳定平台速度环控制系统含有陀螺测量噪声,设计了带有系统参数扰动迭代估计的自适应强跟踪卡尔曼滤波器,并与模型参考控制系统相结合,然后将其与现有的PI控制系统进行扰动隔离性能的系统仿真对比实验及其结果分析.实验结果表明,所提出的自适应强跟踪卡尔曼滤波器可以进一步提高扰动控制系统的隔离度性能,尤其在把非线性摩擦力补偿一半的情况作为未建模的不确定因素影响情况,所设计的滤波器不但能够稳定地工作,而且模型参考自适应控制系统和PI控制系统的隔离度性能都有明显的提高.

... 式中: λk≥1为自适应渐消因子,可由下面算法^[17]确定: ...