基于横摆力矩控制的电动轮汽车转弯节能控制

引用本文

孙文, 王庆年, 王军年. 基于横摆力矩控制的电动轮汽车转弯节能控制[J].吉林大学学报（工学版）, 2018,48(1): 11-19
SUN Wen, WANG Qing-nian, WANG Jun-nian. Yaw-moment control of motorized vehicle for energy conservation during cornering[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 11-19 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170525
Permissions

基于横摆力矩控制的电动轮汽车转弯节能控制

孙文, 王庆年, 王军年

吉林大学汽车仿真与控制国家重点实验室,长春 130022

通讯作者：王军年(1981-),男,教授,博士.研究方向:节能与新能源汽车.E-mail:junnianwang@126.com

作者简介:孙文(1989-),女,博士研究生.研究方向:节能与新能源汽车.E-mail:sun_wendy@126.com

基金:国家自然科学基金项目(51205153); 吉林省自然科学基金项目(20140101072JC)

摘要

首先,研究了车辆转弯时转弯阻力产生的机理,提出了影响转弯阻力的因素。然后,提出了通过改变纵向力分配减小转弯阻力的方法。最后,基于车身稳定性的约束,通过理论分析和计算机仿真,对比了纵向力分配前、后车辆转弯过程中的能耗,并采用遗传算法对后轴轮间的转矩分配系数进行了优化。研究表明,通过对电动轮汽车的纵向力分配,可以降低电动汽车在转弯过程中的能耗,提高转弯机动性。

关键词: 车辆工程; 电动汽车; 四轮独立驱动; 横摆力矩控制; 转弯阻力; 遗传算法

中图分类号:U461.1 文献标志码:A 文章编号:1671-5497(2018)01-0011-09

Yaw-moment control of motorized vehicle for energy conservation during cornering

SUN Wen, WANG Qing-nian, WANG Jun-nian

State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

Abstract

In this paper, based on the study of vehicle dynamics during turning, the reason that causing extra driving resistance was found. It was proposed that a counter yaw moment can mitigate this extra driving resistance during turning. For a vehicle with independent electric drive for left and right wheels on rear axle, driving power can be reduced by means of proper torque distribution between the left and right wheels. By theoretical analysis and simulation, he optimal torque distribution coefficient of the real axle was obtained by genetic algorithm, by which the vehicle consumes the lowest power during turning without causing instability. This research shows that the vehicle energy consumption can be reduced, and turning maneuverability can be improved by the yaw moment control.

Keyword: vehicle engineering; electric vehicle; four-wheel independent drive; yaw moment control; turning resistance; genetic algorithm

Show Figures

0 引言

以电动汽车汽车为代表的新能源汽车, 在节能和环保方面符合当前可持续发展的社会需求, 因而得到了各国政府的充分重视。采用轮毂电机驱动的电动汽车, 因其诸多优点成为当前电动汽车发展的一个重要方向^[1]。

人们已经开发出的车身稳定性控制系统, 如博世公司(BOSCH)的车身电子稳定性系统(ESP)^[2]、丰田公司(Toyota)的车身稳定控制系统(VSC)^[3]、本田公司(Honda)的车辆稳定性控制系统(VSA)和宝马公司(BMW)的动态稳定控制系统(DSC), 均通过施加制动力来控制车身稳定性, 其效果相当于在车辆的纵向上施加阻力。这种被动的控制虽然起到确保车身稳定性的作用, 但也人为地使车辆降速, 主动消耗了发动机传输的能量。直接横摆力偶矩控制(DYC)能够通过主动改变左、右两侧驱动力, 产生横摆力矩, 主动改善车身稳定性^[4]。当前的DYC控制普遍通过差速器来实现, 结构复杂且有一定的能量损失^[5]。

目前电动汽车采用电池作为储能装置, 其续航里程是制约电动汽车发展的一个因素。电动汽车的节能和高效也无法忽视^[6]。对于轮毂电机驱动的汽车, 其各个驱动轮具有独立的动力总成, 通过实时控制各个电机的输出转矩即可达到控制车身稳定性的作用^[7], 避免了附加制动力矩对总能量的损害。同时由于电动轮汽车取消了车辆原有传动系统, 使其传动效率大大提高^[8]。

目前针对电动轮的转矩控制, 普遍通过优化控制和转矩分配来改善和提高车辆的操纵稳定性^[9]。车辆在产生横摆力矩时, 主动改变其原有的转弯特性。如果同时改变方向盘转角, 可使车辆在较小的侧向力作用下维持原有转弯特性。而侧向力的改变将使车辆的转弯阻力下降, 使汽车在转弯过程中的能耗降低。

本文重点研究了车辆转弯时转弯阻力产生的机理, 提出了影响转弯阻力的因素。提出了通过改变纵向力分配减小转弯阻力的方法。本文主要通过理论分析和计算机仿真分析的方法, 基于车身稳定性的约束, 对比了纵向力分配前、后车辆转弯过程中的能耗, 并采用遗传算法对后轴轮间的转矩分配系数进行了优化。

1 转弯阻力产生机理

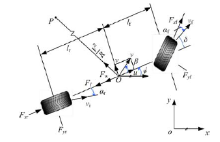
在不改变车辆模型操纵稳定性的基本特性前提下, 为了便于分析和理论推导, 本文采用线性2自由度汽车模型进行研究。

1.1 线性二自由度模型动力学

图1为转弯工况下的线性2自由度模型的受力分析图。

车辆的动力学方程如下所示:

$\begin{matrix} \overset{\cdot}{mV} \end{matrix}$ cosβ -mv( $\begin{matrix} \dot{β} \end{matrix}$ + $\begin{matrix} \dot{ψ} \end{matrix}$ )sinβ =F_x_fcosδ -F_y_fsinδ +F_x_r-(F_f+F_w) (1)

$\begin{matrix} \overset{\cdot}{mV} \end{matrix}$ sinβ +mv( $\begin{matrix} \dot{β} \end{matrix}$ + $\begin{matrix} \dot{ψ} \end{matrix}$ )cosβ =F_x_fsinδ +F_y_fcosδ +F_y_r (2)

J $\begin{matrix} \ddot{ψ} \end{matrix}$ =(F_x_fsinδ +F_y_fcosδ )l_f-F_y_rl_r (3)

式中:m为车辆质量; J为车辆转动惯量; v为车速; β 为质心侧偏角; ψ 为横摆角; δ 为前轮转角; l_f为前轴距; l_r为后轴距; F_x_f为前轴切向力; F_x_r为后轴切向力; F_y_f为前轴侧向力; F_y_r为后轴侧向力; F_f为车辆滚动阻力; F_w为车身风阻。

	Figure Option View Download New Window
	图1 线性2自由度汽车模型Fig.1 2-DOF single track model

假设车辆当前为静态工况, 即匀速圆周行驶。基于上述假设, $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ =0, 同时有 $\begin{matrix} \dot{β} \end{matrix}$ =0和 $\begin{matrix} \ddot{ψ} \end{matrix}$ =0。假设车辆的前轮转角和质心侧偏角很小, 则可有sinδ ≈ δ , cosδ ≈ 1, sinβ ≈ β , cosβ ≈ 1。将上述变量带入式(1)~(3), 可知全部车轮上的切向力之和为:

F_y_r= $\begin{matrix} (F_{xf} δ + F_{yf}) \end{matrix}$ l_f/l_r(4)

将式(4)代入式(1) (2), 则式(1)(2)可改写成如下形式:

-mv $\begin{matrix} \dot{ψ} \end{matrix}$ β =F_x_f-F_y_fδ +F_x_r-(F_f+F_w)(5)

mv $\begin{matrix} \dot{ψ} \end{matrix}$ l_r/l=F_x_fδ +F_y_f(6)

式中:l=l_f+l_r为车辆的轴距。将式(5)(6)进行代换, 忽略前轮转角δ 的平方项, 则车辆的总纵向力为:

F_x_f+F_x_r=F_f+F_w+mv $\begin{matrix} \dot{ψ} \end{matrix} \begin{matrix} (\frac{l_{r}}{l} δ - β) \end{matrix}$ (7)

根据本文所采用的线性2自由度模型的特点, 前后轴的侧偏角可以用质心侧偏角β =w/u和横摆角ψ 来表示:

α _f=δ - $\begin{matrix} (β + \frac{l_{f} \dot{ψ}}{u}) \end{matrix}$ (8)

α _r= $\begin{matrix} \frac{l_{r} \dot{ψ}}{u} \end{matrix}$ -β (9)

式中:u为车辆质心处的纵向速度; w为车辆质心处的侧向速度。则车辆的质心侧偏角可以由其前后轴的侧偏角来表示:

β = $\begin{matrix} \frac{l_{r}}{l} \end{matrix}$ δ - $\begin{matrix} \frac{l_{r}}{l} \end{matrix}$ α _f- $\begin{matrix} \frac{l_{f}}{l} \end{matrix}$ α _r(10)

同时, 车辆的转弯半径也可如下表示,

R=v/ $\begin{matrix} \dot{ψ} \end{matrix}$ (11)

式中: $\begin{matrix} \dot{ψ} \end{matrix}$ 为车辆的横摆角速度。将式(10)和式(11)代入式(7), 则车辆的总纵向力可表示为:

F_x_f+F_x_r=F_f+F_w+m $\begin{matrix} \frac{V^{2}}{R} \end{matrix} \begin{matrix} (\frac{l_{r}}{l} α_{f} + \frac{l_{f}}{l} α_{r}) \end{matrix}$ (12)

1.2 转弯降速现象及转弯阻力产生机理

根据驾驶员的驾驶经验, 即使维持油门踏板开度不变, 车辆在由直线进入弯道并完成转弯行驶的过程中, 车速会产生小幅下降。并且越小的转弯半径, 所带来的车速降幅越明显, 这就是转弯降速现象。通过式(12)可以看出, 侧向力的一个分量是产生这一降速现象的原因。在平路上匀速直线行驶时, 切向力之和等于滚动阻力与风阻之和, 即:

F=F_f+F_w(13)

当车辆转弯行驶时, 则产生式(12)中等号右侧第3个分量, 即为转弯阻力F_r:

F_r=m $\begin{matrix} \frac{V^{2}}{R} \end{matrix} \begin{matrix} (\frac{l_{r}}{l} δ - β) \end{matrix}$ =m $\begin{matrix} \frac{V^{2}}{R} \end{matrix} \begin{matrix} (\frac{l_{r}}{l} α_{f} + \frac{l_{f}}{l} α_{r}) \end{matrix}$ (14)

类似于滚动阻力, 定义转弯阻力系数:

f_r= $\begin{matrix} \frac{F_{r}}{G} \end{matrix}$ = $\begin{matrix} \frac{V^{2}}{Rg} \end{matrix} \begin{matrix} (\frac{l_{r}}{l} δ - β) \end{matrix}$ = $\begin{matrix} \frac{V^{2}}{Rg} \end{matrix} \begin{matrix} (\frac{l_{r}}{l} α_{f} + \frac{l_{f}}{l} α_{r}) \end{matrix}$ (15)

当车辆在转弯行驶, 假设地面附着良好, 则不存在车轮打滑所产生的能耗。由式(14)可以看出, 转弯阻力仅与前轮转角δ 或转弯半径, 质心侧偏角β 以及车速v有关。

假设车辆的质心位于前后轴中心, 即l_f=l_r=0.5l, 且车辆为中性转向α _f=α _r, 则式(15)可表示为:

f_r= $\begin{matrix} (V^{2} / Rg) \end{matrix}$ α _f(16)

根据汽车理论的推导, 车轮的侧偏角α 与轮胎侧向力F_y呈线性关系, 即:

α = $\begin{matrix} \frac{1}{C_{α}} \end{matrix}$ F_y(17)

同时, 车辆的侧向力F_y也与侧向加速度a_y为线性关系:

∑ F_y=ma_y=m $\begin{matrix} \frac{v^{2}}{R} \end{matrix}$ =G $\begin{matrix} \frac{v^{2}}{Rg} \end{matrix}$ (18)

结合式(16)~(18), 转弯阻力系数与侧偏角的平方或侧向加速度的平方线性相关, 即为:

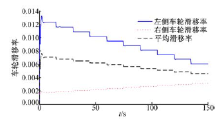
f_r∝ $\begin{matrix} {(\frac{v^{2}}{Rg})}^{2} \end{matrix}$ 或f_r∝ α ²(19)

基于上述理论分析, 车辆转弯过程中的滚动阻力系数和转弯阻力系数可以绘制成曲线, 如图2所示。

	Figure Option View Download New Window
	图2 滚动阻力系数和转弯阻力系数与侧向加速度关系曲线Fig.2 Turning resistance and rolling resistance coefficient vs. lateral acceleration

图2中的曲线仿真工况为:车辆绕半径为50 m的定圆加速行驶, 其加速度为2.8 m/s², 初始车速为0, 保持轮胎的侧偏角在线性范围内(不大于4° )。从图2可以看出, 转弯阻力系数随侧向加速度的增大呈现出抛物线增长趋势, 而滚动阻力系数并不随侧向加速度增大而变化。在车辆具有较小的侧向加速度时, 转弯阻力系数远小于滚动阻力系数。而且随着侧向加速的增大, 转弯阻力系数明显增大并且其数值也大于滚动阻力系数。

2 纵向力分配对转弯阻力的抑制作用

基于前文的分析可知, 转弯阻力系数f_r与方向盘转角δ 为正相关函数, 因此可以采用适当减小车辆在转弯过程中的方向盘转角的方式减小车辆的转弯阻力。但是驾驶员在实际驾驶过程中, 需要根据路况和预定轨迹完成驾驶动作, 即当方向盘转角减小时, 还能够使车辆维持恒定的横摆角速度, 从而完成相同的转弯轨迹。

如式(3)所示, 车辆的横摆角速度是由车辆的纵向力和侧向力共同影响的。对车辆内外侧后轮施加一个差动力Δ F_x_r, 从而产生一个附加横摆力矩M_z, 则式(3)可以改写成如下形式:

J $\begin{matrix} \ddot{ψ} \end{matrix}$ = $\begin{matrix} (F_{xf} sinδ + F_{yf} cosδ) \end{matrix}$ l_f-F_y_rl_r+Δ M (20)

式中:Δ M=Δ F_x_rd/2, 其中d为车辆的轮距, 本文认为车辆的前、后轴轮距相等。

本文在对后轴施加差动力Δ F_x_r时, 并不改变车辆的总驱动力, 即内外侧车轮的驱动力如下所示:

F_{x_}_out+F_{x_}_in=F_x_r(21)

F_{x_}_out-F_{x_}_in=Δ F_x_r (22)

式中:F_{x_}_in和F_{x_}_out分别为内、外侧车轮的驱动力。

结合式(1) (2) (12), 式(7)所示的各个车轮的合纵向力可以表示为:

F_x_f+F_x_r=F_f+F_w+mv $\begin{matrix} \dot{ψ} \end{matrix} \begin{matrix} (\frac{l_{r}}{l} δ - β) \end{matrix}$ - $\begin{matrix} \frac{Δ F_{xr} d}{2 l} \end{matrix}$ δ (23)

则式(14)所示的转弯阻力也可以改写成如下形式:

F_r=m $\begin{matrix} \frac{v^{2}}{R} \end{matrix} \begin{matrix} (\frac{l_{r}}{l} δ - β) \end{matrix}$ - $\begin{matrix} \frac{d}{2 l} \end{matrix}$ δ Δ F_x_r=m $\begin{matrix} \frac{v^{2}}{R} \end{matrix} \begin{matrix} (\frac{l_{r}}{l} α_{f} + \frac{l_{f}}{l} α_{r}) \end{matrix}$ - $\begin{matrix} \frac{d}{2 l} \end{matrix}$ δ Δ F_x_r (24)

对比分析式(24)和式(14)可知, 对车辆施加横摆力矩可以减小转弯阻力。公式中的质心侧偏角β 与前轮转角δ 相比非常小。尽管对车辆施加横摆力矩可能在一定程度上增大后轴侧偏角α _r, 但也同时减小了前轴侧向力, 从而减小了前轴侧偏角α _f。综上, 由式(24)可以看出, 当车辆转弯时, 可以通过合理改变车辆内、外侧车轮的驱动力, 减小车辆的转弯阻力。同时式(24)也说明, 车辆的横摆角速度与纵向力的差值有关, 而与各轮输出的转矩大小无关。本文所探讨的纵向力分配问题, 均为车辆稳定情况下进行的。

3 基于能耗的车辆转矩分配系数优化

基于前文分析的影响转弯阻力的因素, 当车辆转弯行驶时, 方向盘转角与车辆的转弯阻力成正比。在整车能耗方面将表征为, 车辆以相同车速入弯并行驶等长轨迹, 如果保持油门踏板开度不变, 那么随着转弯半径的减小, 车速降幅增大; 当车辆维持入弯车速不变并行驶等长轨迹, 那么随着转弯半径的减小, 消耗功率将增大。

针对电动轮驱动车辆, 由于其采用电机MAP, 需要对后轴的转矩分配系数进行优化, 使得车辆在减小转弯阻力的同时, 电机的耗能最低。针对模型和目标函数的特点, 本文采用遗传算法对转矩分配系数进行优化。

本文的优化对象为转矩分配系数k, 其表示形式如下所示:

k= $\begin{matrix} \frac{ΔT}{T_{t}} \end{matrix}$ = $\begin{matrix} \frac{T_{out} - T_{in}}{T_{out} + T_{in}} \end{matrix}$ (25)

式中:T_in和T_out分别为内、外侧电机的驱动转矩(本文不考虑电机减速装置)。

转矩分配系数的优化目标是在满足汽车转弯半径不变的基础上, 尽量减小转弯阻力和电机能耗。为了便于分析, 定义电机能耗为车辆转弯时的等效百公里能耗。优化目标如下所示:

$\begin{matrix} \min_{k} \end{matrix}$ J(k)=∫ _tP_m1(k)+∫ _tP_m2(k)

s.t. $\begin{matrix} \{\begin{matrix} 0 \leq k \leq 1 \\ T_{m_min} \leq T_{m 1}, T_{m 2} \leq T_{m_max} \\ T_{m 1} + T_{m 2} \leq T_{t} \\ 0 ° \leq β \leq 12 ° \\ Δ ω_{r} \leq ε \end{matrix} \end{matrix}$ (26)

式中:k为转矩分配系数; J $\begin{matrix} (k) \end{matrix}$ 为车辆的等效百公里能耗; T_m_{_}_min和T_m_{_}_max为单个电机的转矩极限值; T_t为后轴的总驱动转矩; t为车辆转弯耗时; P_m1(k)和P_m2(k)为后轴两侧车轮电机的瞬时功率, 其计算表达式如下:

P_m_i= $\begin{matrix} \frac{T_{mi} n_{i}}{9550 η_{i}} \end{matrix}$ (27)

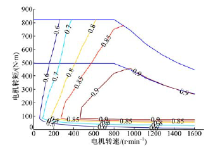
式中:n_i为电机转速; η _i为第i个车轮的效率, 其数值大小通过图3的电机MAP图查表得出。

	Figure Option View Download New Window
	图3 电机MAP图Fig.3 Motor efficiency map

式(26)的最后两个约束条件为稳定性要求。根据采用的仿真软件的模型, 质心侧偏角通常为正, 且根据文献选取其小于12° ^{[10, 11]}。本文在仿真过程中, 由于要求车辆的车速和转弯半径不变, 则横摆角速度认为基本不变, 其变化范围仅在一个较小的范围ε 内。

通过离线优化得出的最佳转矩分配系数k将被做成一个表格, 在实际应用中采用查表的方式进行。进而车辆的转矩分配控制器通过查表计算出最佳转矩分配比κ :

κ =T_in/T_out=(1-k)/(1+k) (28)

最终, 内、外侧车轮的实际需求转矩可以通过下式求得:

$\begin{matrix} \{\begin{matrix} T_{out} = \frac{1}{κ + 1} T_{t} \\ T_{in} = \frac{κ}{κ + 1} T_{t} \end{matrix} \end{matrix}$ (29)

4 仿真结果与分析

在车辆的实际行驶过程中, 转弯工况出现的概率是非常高的。尽管单个转弯工况持续的时间非常短, 能节省的能量也并不大, 但是通过累积全工况下的转弯工况, 其节能潜力也是不可忽视的。本节仿真首先采用J-turn实验来验证车辆的转弯降速现象和转弯能耗高的现象。并通过定半径圆周实验来说明转矩分配系数对车辆转弯能耗的影响。最终结合实际的电机MAP, 说明电机本身的效率变化对整体能耗带来的影响。

4.1 J-turn实验

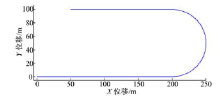
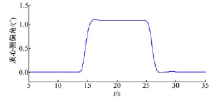
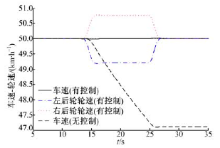
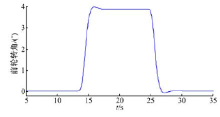
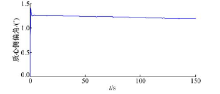
本文定义了如图4所示的J-turn轨迹, 设定仿真车速为50 km/h。质心侧偏角、车速曲线、前轮转角、电机转矩变化情况等, 如图5~图8所示。

	Figure Option View Download New Window
	图4 J-turn实验仿真轨迹Fig.4 J-turn simulation trajectory

从图5可知, 车辆在该仿真工况下, 质心侧偏角变化很小, 始终处于稳态情况。如图6所示, 当保持油门踏板开度不变时, 不对转矩进行控制, 则车辆在转弯过程中, 车速将由于转弯阻力而下降。通过对车辆内外侧转矩进行差动控制, 在同样的油门踏板开度情况下, 其车速仅在入弯和出弯处有小幅波动, 其过弯的速度明显高于未控制的情况。结合图6和图7可以看出, 当采用车速闭环控制的驾驶员模型后, 车速仅在入弯和出弯的时候有小幅的波动。为了实现车速跟随, 电机需要在车辆转弯过程中输出更多的转矩, 用于克服转弯阻力, 如图8所示。综上, 随着前轮转角的增大, 车辆所受到的转弯阻力也随之增大。

	Figure Option View Download New Window
	图5 质心侧偏角Fig.5 Sideslip angel

	Figure Option View Download New Window
	图6 车速和轮速曲线Fig.6 Vehicle speed and wheel speed of the driving wheels

	Figure Option View Download New Window
	图7 前轮转角变化曲线Fig.7 Steering wheel angle

	Figure Option View Download New Window
	图8 电机驱动转矩Fig.8 Motor traction torque with close-loop vehicle speed control

4.2 定半径圆周实验

在当前仿真工况下, 不考虑电机效率对能耗的影响。本文对比进行了一系列半径为30~50 m的圆周实验。设定目标车速为50 km/h。

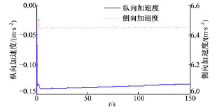
图9为车速50 km/h、半径30 m时调整转矩分配比例后的各性能变化情况。如图10所示, 在仿真过程中, 车速始终保持为50 km/h, 进行转矩轮间分配对车速并无影响。如图11所示, 在转矩转移的过程中, 车辆的横摆角速度也没有明显变化。从图12可知, 前轮转角随着转矩分配系数的增大而减小, 同时车辆仍能保持原轨迹行驶。从图13可知, 车辆的质心侧偏角有小幅下降。结合图12和图13可以看出, 车辆的横摆角速度与质心侧偏角之间并无明显波动, 因此车辆在进行转矩转移的过程中, 并未出现失稳。如图14所示, 随着转矩分配系数的增大, 车辆的纵向加速度减小, 而车辆的侧向加速度保持不变。从图15可以看出, 随着转矩分配系数的增大, 车辆所受到的转弯阻力下降, 使得电机的需求功率下降。本节的仿真为车辆左转弯工况, 根据车辆动力学原理, 由于轮荷转移, 在转弯过程中, 内侧(左侧)车轮的滑移率将比外侧(右侧)车轮的滑移率小幅提高。图16为转矩转移过程中的内外侧车轮滑移率变化情况。从图16可以看出, 随着转矩由内侧车轮向外侧车轮转移, 车辆的平均滑移率明显下降。由此可知, 转矩的轴距分配也能有效降低车辆的平均滑移率, 从而节约一定能耗。

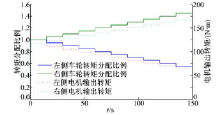	Figure Option View Download New Window
	图9 内、外侧车轮转矩分配比及输出转矩Fig.9 Toque deviation ratio command and actual traction torque of the driving wheels

	Figure Option View Download New Window
	图10 车速曲线Fig.10 Curve of vehicle speed

	Figure Option View Download New Window
	图11 横摆角速度曲线Fig.11 Curve of yaw rate

	Figure Option View Download New Window
	图12 前轮转角曲线Fig.12 Curve of steering road wheel angle

	Figure Option View Download New Window
	图13 质心侧偏角曲线Fig.13 Curve of sideslip angle

	Figure Option View Download New Window
	图14 纵向加速度和侧向加速度曲线Fig.14 Curve of longitudinal acceleration and lateral acceleration

	Figure Option View Download New Window
	图15 电机总功率需求Fig.15 Total electric power consumption

	Figure Option View Download New Window
	图16 车轮滑移率Fig.16 Wheel slip ratio

表1为车速50 km/h、不同转弯半径下的能耗情况。本节的仿真不考虑电机工作点变化所带来的电机效率变化。

为了便于理解, 表中能耗为车辆的等效百公里能耗, 即车辆维持定圆行驶100 km的能耗。从表1可以看出, 转矩分配系数越大, 车辆的等效百公里能耗越低, 即转矩的轮间分配可以有效减小车辆的转弯阻力, 从而达到节能的目的。

表2和表3分别为车速为40、30 km/h时, 不同转弯半径的能耗情况。可知, 车速越低, 通过转矩轴间分配所节约的能耗越少, 这与式(19)所说明的原理一致。

表1 车速50 km/h时不同转弯工况能耗(不考虑电机效率) Table 1 Power consumption of cornering test with different radii at 50 km/h

表2 车速40 km/h时不同转弯工况能耗(不考虑电机效率) Table 2 Power consumption of cornering test with different radii at 40 km/h

表3 车速30 km/h时不同转弯工况能耗(不考虑电机效率) Table 3 Power consumption of cornering test with different radii at 30 km/h

4.3 带有电机MAP的定半径圆周实验

根据上文的分析, 对车辆进行轮间转矩分配, 可以有效降低车辆的转弯阻力, 从而节约车辆转弯过程中的能耗。根据上一节的仿真可以发现, 在改变车轮需求转矩的同时, 轮毂电机的电机工作点也将发生变化。因此本节将讨论电机MAP对能耗的影响, 并进行了一系列与4.2节类似的仿真实验, 表4和表5为仿真结果。表4的最后一行为通过遗传算法得出的最佳转矩分配比。

表4 车速50 km/h下不同转弯工况能耗(考虑电机效率) Table 4 Power consumption of cornering test with different radii at 50 km/h

结合表4和图3的电机MAP图, 当车速为50 km/h进行半径50 m转弯仿真时, 电机的初始工作点位于低效区, 随着转矩分配系数的增大, 左侧电机的工作点仍处于低效区, 但右侧电机的工作点进入高效区, 因此整体呈现出更大的节能效果。当车速为50 km/h进行半径30 m转弯仿真时, 电机的初始工作点就位于高效区附近, 随着转矩逐渐从左侧车轮转移至右侧车轮, 左轮的电机工作点逐渐进入低效区, 而右侧的电机工作点仍处于高效区, 总的电机能耗呈现出增加的趋势。

表5所示的工况与表4的第一组数据相类似, 由于电机的初始工作点位于低效区, 当转矩从左侧车轮向右侧车轮转移的过程中, 右侧电机的工作点向高效区移动, 因此总的能耗呈现逐渐下降的趋势。

表5 车速40 km/h下不同转弯工况能耗(考虑电机效率) Table 5 Power consumption of cornering test with different radii at 40 km/h

对比4.2节和4.3节的仿真实验, 各个不同工况下的能耗可以通过表6得出。

表6 不同车速和转弯半径下最佳能耗及转矩分配比 Table 6 Energy conservation comparison of cornering test with different radii at different speeds between two optimization conditions

仿真工况	不考虑电机效率的能耗和转矩分配比(参考4.2节)		考虑电机效率的能耗和转矩分配比(参考4.3节)
50 m	0.86% @ 0.0∶ 2.0	0.16%@ 0.0∶ 2.0	14.06%@ 0.0∶ 2.0	25.34%@ 0.0∶ 2.0
30 m	1.73% @ 0.4∶ 1.6	0.40% @ 0.0∶ 2.0	0.21%@ 0.8∶ 1.2	13.56%@ 0.0∶ 2.0
仿真车速 /(km· $\begin{matrix} {h^{-}}^{1} \end{matrix}$ )	50	40	50	40

表6的第1列为不考虑电机效率变化的能耗情况, 可以看出, 外侧车轮的转矩越大, 总能耗越低。但转矩分配比例的极限值由车辆稳定性来约束。同时类似主动控制系统, 在转矩分配的过程中, 没有额外的能量输出要求。对比表6左、右两列数据可以看出, 是否考虑电机效率对最终的能耗影响非常大。

5 结束语

本文通过理论分析和仿真验证最终得出, 车辆在转弯过程中受到额外的转弯阻力的影响, 而转弯阻力的大小与车速、转弯半径或前轮转角、质心侧偏角有关。因此当车辆过弯时, 如果仍要维持原有车速, 则需要输出更多的驱动力矩。通过对内、外侧车轮施加不同纵向力, 产生横摆力矩, 可以使得车辆在保证原有的操纵稳定性的情况下, 节约一定的能耗, 即纵向力分配可以对车辆产生节能的效果。通过采用遗传算法, 可以在车辆不同车速、不同转弯半径的工况下得出最佳的转矩分配比例, 为具有左右转矩矢量控制功能的电动汽车提供转矩控制的依据。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	罗玉潭, 谭迪. 一种带新型内置悬置系统的电动轮结构研究[J]. 汽车工程, 2013, 36(12): 1105-1110. Luo Yu-tan, Tan Di. A research on the hub-motor driven wheel structure with a novel built-in mounting system[J]. Automotive Engineering, 2013, 36(12): 1105-1110. [本文引用:1]
[2]	孙文, 王军年, 王庆年, 等. 电动轮驱动系统结构设计与仿真研究[J]. 汽车工程, 2016, 38(3): 330-336. Sun Wen, Wang Jun-nian, Wang Qing-nian, et al. A study on the structural design and simulation of in-wheel motor drive system[J]. Automotive Engineering, 2016, 38(3): 330-336. [本文引用:1]
[3]	Singh B, Naidu N K S. Direct power control of single VSC based DFIG without rotor position sensor[C]∥IEEE International Conference on Power Electronics, Drives and Energy Systems, Bengaluru, India, 2012: 1-6. [本文引用:1]
[4]	余卓平, 姜炜, 张立军. 四轮轮毂电机驱动电动汽车扭矩分配控制[J]. 同济大学学报: 自然科学版, 2008, 36(8): 1115-1119. Yu Zhuo-pin, Jiang Wei, Zhang Li-jun. Torque distribution control for four wheel in-wheel-motor electric vehicle[J]. Journal of Tongji University (Natural Science), 2008, 36(8): 1115-1119. [本文引用:1]
[5]	Koichi Ono. Electric drive system forsport hybrid SH-AWD[C]∥SAE Paper, 2014-01-1821. [本文引用:1]
[6]	卢东斌, 欧阳明高, 谷靖, 等. 四轮驱动电动汽车永磁无刷轮毂电机转矩分配[J]. 清华大学学报: 自然科学版, 2012, 52(4): 451-456. Lu Dong-bin, Ou-yang Ming-gao, Gu Jing, et al. Torque distribution algorithm for a permanent brushless DC hub motor for four-wheel drive electric vehicle[J]. Journal of Tsinghua University(Sci & Tech), 2012, 52(4): 451-456. [本文引用:1]
[7]	Kiumars Jalali, Thomas Uchida, Steve Lambert, et al. Development of an advanced torque vectoring control system for an electric vehicle with in-wheel motors using soft computing techniques[C]∥SAE Paper, 2013-01-0698. [本文引用:1]
[8]	Christophe Moure, Klaus Kersting. Development of functional safety in a multi-motor control system for electric vehicles[C]∥SAE Paper, 2012-01-0028. [本文引用:1]
[9]	Athari Abtin, Fallah Saber, Li Bin, et al. optimal torque control for an electric-drive vehicle with in-wheel motor: implementation and experiments [C]∥ SAE Paper, 2013 -01-0674 [本文引用:1]
[10]	Jin L Q, Liu Y. Study on adaptive slid mode controller for improving hand ling stability of motorized electric vehicles[J]. Mathematical Problems in Engineering, 2014, 2014: 1-10. [本文引用:1]
[11]	Shibahata Y, Shimada K, Tomari T. Improvement of vehicle maneuverability by direct yaw moment control[J]. Vehicle System Dynamics, 1993, 22(5/ 6): 465-481. [本文引用:1]

2013

0.0

. 2013, 36(12):1105-1110

A research on the hub-motor driven wheel structure with a novel built-in mounting system

一种带新型内置悬置系统的电动轮结构研究

Luo Yu-tan , Tan Di.

罗玉潭, 谭迪

... 采用轮毂电机驱动的电动汽车,因其诸多优点成为当前电动汽车发展的一个重要方向^[1] ...

2016

0.0

. 2016, 38(3):330-336

A study on the structural design and simulation of in-wheel motor drive system

电动轮驱动系统结构设计与仿真研究

Sun Wen , Wang Jun-nian , Wang Qing-nian

孙文, 王军年, 王庆年

根据某四轮轮毂电机驱动的纯电动试验车的车型参数和性能要求,对其电动轮驱动系统进行了匹配选型和结构方案设计.然后针对轮毂电机轴的3种受力工况分析,对电机轴和其他零部件进行了再设计.最后使用CATIA软件建立了电动轮模型,采用Adina软件对电机轴和转子壳体进行了有限元分析.所采用结构设计和强度与疲劳寿命校核方法为电动轮驱动系统的正向开发提供了参考.

... 人们已经开发出的车身稳定性控制系统,如博世公司(BOSCH)的车身电子稳定性系统(ESP)^[2]、丰田公司(Toyota)的车身稳定控制系统(VSC)^[3]、本田公司(Honda)的车辆稳定性控制系统(VSA)和宝马公司(BMW)的动态稳定控制系统(DSC),均通过施加制动力来控制车身稳定性,其效果相当于在车辆的纵向上施加阻力 ...

2012

0.0

2008

0.0

. 2008, 36(8):1115-1119

Torque distribution control for four wheel in-wheel-motor electric vehicle

四轮轮毂电机驱动电动汽车扭矩分配控制

Yu Zhuo-pin , Jiang Wei , Zhang Li-jun.

余卓平, 姜炜, 张立军

... 直接横摆力偶矩控制(DYC)能够通过主动改变左、右两侧驱动力,产生横摆力矩,主动改善车身稳定性^[4] ...

2014

0.0

... 当前的DYC控制普遍通过差速器来实现,结构复杂且有一定的能量损失^[5] ...

2012

0.0

. 2012, 52(4):451-456

Torque distribution algorithm for a permanent brushless DC hub motor for four-wheel drive electric vehicle

四轮驱动电动汽车永磁无刷轮毂电机转矩分配

Lu Dong-bin , Ou-yang Ming-gao, Gu Jing

卢东斌, 欧阳明高, 谷靖

... 电动汽车的节能和高效也无法忽视^[6] ...

2013

0.0

... 对于轮毂电机驱动的汽车,其各个驱动轮具有独立的动力总成,通过实时控制各个电机的输出转矩即可达到控制车身稳定性的作用^[7],避免了附加制动力矩对总能量的损害 ...

2012

0.0

... 同时由于电动轮汽车取消了车辆原有传动系统,使其传动效率大大提高^[8] ...

2013

0.0

... 目前针对电动轮的转矩控制,普遍通过优化控制和转矩分配来改善和提高车辆的操纵稳定性^[9] ...

2014

0.0

... ^[10,11] ...

1993

0.0

... ^[10,11] ...