基于集成式线控液压制动系统的轮胎滑移率控制

引用本文

何祥坤, 季学武, 杨恺明, 武健, 刘亚辉. 基于集成式线控液压制动系统的轮胎滑移率控制. 2018, 48(2): 364-372
HE Xiang-kun, JI Xue-wu, YANG Kai-ming, WU Jian, LIU Ya-hui. Tire slip control based on integrated-electro-hydraulic braking system. Journal of Jilin University Engineering and Technology Edition, 2018, 48(2): 364-372 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170060
Permissions

基于集成式线控液压制动系统的轮胎滑移率控制

何祥坤, 季学武, 杨恺明, 武健, 刘亚辉

清华大学汽车安全与节能国家重点实验室,北京 100084

通信作者:季学武(1964-),男,副教授,博士生导师. 研究方向:汽车底盘电控系统开发与动力学控制.E-mail:jixw@tsinghua.edu.cn

作者简介:何祥坤(1989-),男,博士研究生. 研究方向:汽车动力学控制与智能驾驶技术. E-mail:hxk15@mails.tsinghua.edu.cn

基金项目:中国汽车产业创新发展联合基金项目(U1664263); 国家自然科学基金项目(51375009); 国际合作项目(20153000021); 清华大学自主科研计划项目(20161080033); 山东省自然科学基金项目(ZR2016EEQ06)

摘要

传统的车辆制动系统很难以轮胎滑移率为直接控制目标,为了提高汽车的主动安全性能,对集成式线控液压制动系统(IEHB)的轮胎滑移率控制机理进行深入研究。在建立IEHB执行机构物理仿真模型与7自由度整车动力学模型的基础上,结合分层控制构架,利用滑移率与制动转矩构成的双闭环非线性控制方法,设计了基于IEHB系统的轮胎滑移率控制器;通过AMESim与MATLAB/Simulink联合仿真平台,分别在高附着、低附着路面进行高速主动紧急制动仿真试验。结果表明:本文提出的控制方法可有效调控汽车轮胎滑移率。

关键词: 车辆工程; 集成式线控液压制动系统; 轮胎滑移率; 分层控制构架; 双闭环非线性控制

中图分类号:U461 文献标志码:A 文章编号:1671-5497(2018)02-0364-09

Tire slip control based on integrated-electro-hydraulic braking system

HE Xiang-kun, JI Xue-wu, YANG Kai-ming, WU Jian, LIU Ya-hui

State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China

Abstract

The traditional vehicle braking system is difficult to control the tire slip rate directly. In order to study the tire slip control mechanism of the Integrated-Electro-Hydraulic Braking (IEHB) system and the improve active safety performance of the vehicle, the physical simulation model of IEHB actuator and dynamic model of 7 DOF vehicle were established. Combining with the hierarchical control structure and taking the control method of dual loop, which constitutes slip rate and braking torque, the tire slip nonlinear controller based on IEHB is designed. Simulation test is conducted via co-simulation platform of MATLAB/Simulink and AMESim under the scenarios of active emergency braking process on high adhesion coefficient road and low adhesion coefficient road. Simulation results verify the proposed control method.

Key words: vehicle engineering; integrated-electro-hydraulic brake system; tire slip ratio; hierarchical control structure; dual loop nonlinear control

Show Figures

0 引言

随着能源、环境、行车安全、交通拥堵等问题的日益突出, 智能电动汽车逐渐成为热门话题, 同时也对车辆底盘控制系统提出了更高的要求^{[1, 2, 3]}。智能电动汽车要求制动系统取消对发动机真空度的依赖, 在制动能量回收过程中踏板感觉不受电机制动与摩擦制动协调的影响, 并且制动系统能够实现快速、准确的主动制动控制。上述要求是传统汽车制动系统难以实现的, 因此促使了新一代制动系统的出现。能够满足上述要求的新一代制动系统可以分为两大类:一是线控液压制动系统, 主要在传统汽车制动轮缸的基础上进行改进; 二是线控机械制动系统, 对传统汽车制动系统进行彻底革新, 每个车轮配备一套电控制动执行机构^{[4, 5, 6]}。

电子液压制动(Electro-hydraulic brake, EHB)系统是20世纪90年代开始研究并投入使用的一种线控液压制动系统。博世公司在1996年发表了最早的相关研究论文^[7], 丰田首先将EHB系统投入使用^[8]。而达姆施塔特技术大学、汉阳大学、吉林大学、清华大学等科研机构均对EHB系统控制进行了大量的研究工作^{[9, 10, 11, 12, 13]}。

作为一种新型的电子液压制动系统, 集成式线控液压制动系统(Integrated-electro-hydraulic brake, IEHB)系统的伺服电动增压装置与主缸集成在一起, 在保证整体结构紧凑的同时, 通过联合液压调节单元, 能够快速、准确地调节输出制动压力, 所以IEHB可以更好地集成ABS(Anti-lock braking system)、ESP(Electronic stability program)、RBS(Regenerative braking system)、ACC(Adaptive cruise control)、AEB(Autonomous emergency braking)等整车控制功能^[14]。因此, 近些年来世界各大知名汽车零部件公司都陆续推出了IEHB相关的产品样机, 比如博世的iBooster、大陆的 MK-C1、LSP公司的IBS等。但是这些系统样机都还没有被量产, 相关技术也处于保密阶段。通过查阅文献, 国内外科研机构也积极开展了相关研究。Li等^[15]通过 MATLAB/Simulink 与 CarSim 联合仿真的方法, 对IEHB 执行机构的关键参数进行了分析, 并对整车运动控制问题进行了研究。熊璐等^[16]通过IEHB系统特性分析, 利用颤振补偿方法对IEHB系统进行液压力优化控制研究。Yang^[17]等针对IEHB的伺服电动建压装置利用 Lyapunov 函数设计了滑模控制器, 并与传统 PID 控制器的控制效果进行了对比。

由于轮胎特性直接影响汽车的动力学特性, 而车轮滑移率对轮胎力有明显影响, 因此轮胎滑移率成为车辆动力学控制系统的关键被控变量之一。但机电液系统本身的非连续性和滞后性致使传统汽车制动系统很少以轮胎滑移率为直接控制目标^[13]。为了解决上述问题, 并进一步探究IEHB系统相关技术, 实现基于IEHB系统的轮胎滑移率控制, 本文首先介绍了研究所采用的新型IEHB系统; 之后在Simulink中建立了7自由度整车模型和非线性轮胎模型, 并通过数学模型明确IEHB执行机构的关键参量及不同参量之间的关系, 同时在AMESim复杂系统建模与仿真平台中建立了IEHB系统的物理仿真模型; 基于分层控制构架, 并利用滑移率与制动转矩构成的双闭环非线性控制方法设计了基于IEHB系统的轮胎滑移率控制器; 最后通过MATLAB/Simulink与AMESim联合仿真平台, 分别在高附着、低附着路面进行仿真试验, 验证本文所提出的控制策略的有效性。

1 IEHB系统介绍

1.1 IEHB系统组成

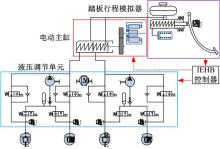
本文所采用的IEHB系统方案简图如图1所示, 主要包括:

(1)踏板行程模拟器:通过位移传感器信号识别驾驶员的制动意图, 通过踏板模拟器模拟制动踏板感觉。

(2)电动主缸:实现液压源输出压力的精细调节。

	Figure Option View Download New Window
	图1 IEHB系统方案简图Fig.1 Schematic diagram of IEHB system

(3)液压调节单元:利用压力传感器监测每个轮缸的制动液压力, 并通过调节轮缸压力使实际制动力矩跟踪目标值。

(4)IEHB 系统控制器:根据驾驶员操纵和整车运动需求对制动系统实施控制。

1.2 IEHB执行机构工作原理

在IEHB执行机构增压时, 电动主缸中的伺服电机转矩增加, 液压调节单元中的进液阀(常开阀)打开, 出液阀(常闭阀)关闭。在IEHB执行机构进行保压操作时, 电动主缸停止工作, 液压调节单元中的进液阀和出液阀同时关闭。在IEHB执行机构减压时, 进液阀关闭, 出液阀打开, 回油泵工作, 同时通过电动主缸进行主动减压操作, 从而实现系统的快速减压。IEHB通过执行增压、保压、减压操作实现对轮胎滑移率的有效调节, 进而对汽车动力学状态进行控制。

2 系统建模及分析

2.1 整车动力学模型

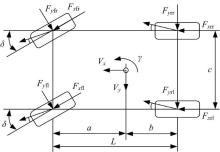
在轮胎滑移率控制器设计过程中, 需要考虑车辆车轮的运动状态、各车轮垂向载荷的变化及制动时汽车的方向稳定性, 因此选择建立7自由度车辆模型(见图2), 动力学方程描述为^[18]:

m( $\begin{matrix} {\overset{\cdot}{V}}_{x} \end{matrix}$ -γ V_y)=(F_x_fl+F_x_fr)cosδ -(F_y_fl+F_y_fr)sinδ +F_x_rl+F_x_rr(1)

m( $\begin{matrix} {\overset{\cdot}{V}}_{y} \end{matrix}$ +γ V_x)=(F_x_fl+F_x_fr)sinδ +(F_y_fl+F_y_fr)cosδ +F_y_rl+F_y_rr (2)

J_z=a(F_x_fl+F_x_fr)sinδ + a(F_y_fl+F_y_fr)cosδ -b(F_y_rl+F_y_rr)+(F_x_fr-F_x_fl)cosδ +(F_x_rr-F_x_rf)+(F_y_fl-F_y_fr)sinδ (3)

J_w $\begin{matrix} {\overset{\cdot}{ω}}_{ij} \end{matrix}$ =T_d_ij-T_b_ij-r_wF_xij(4)

式中:m为整车质量; δ 为前轮转角; a、b分别为前、后轴距; c为轮距; J_z为整车横摆转动惯量; V_x、V_y、γ 分别为车辆纵向速度、侧向速度、横摆角速度; F_xij、F_yij分别为轮胎纵向力、侧向力; J_w为车轮转动惯量; ω _ij为车轮转速; T_d_ij为驱动力矩; T_b_ij为制动力矩; r_w为轮胎有效半径; i=f, r分别表示前、后轴; j=l, r分别表示左、右车轮。

	Figure Option View Download New Window
	图2 7自由度车辆模型Fig.2 7 DOF vehicle model

2.2 非线性轮胎模型

为了反映真实的轮胎动力学特性, 本文采用Pacejka魔术公式描述轮胎的非线性动力学行为^[19], 其统一表达式如下:

y(x)=Dsin[Carctan(φ )](5)

φ =Bx-E[Bx-arctan(Bx)](6)

Y(X)=y(X+S_H)+S_V(7)

λ = $\begin{matrix} \frac{V_{sx}}{V_{xw}} \end{matrix}$ = $\begin{matrix} \frac{V_{xw} - V_{rw}}{V_{xw}} \end{matrix}$ (8)

α =arctan $\begin{matrix} \frac{V_{yw}}{V_{xw}} \end{matrix}$ (9)

V_rw=ω r_w(10)

其中, 轮胎纵向力因子为:

$\begin{matrix} \{\begin{matrix} C_{x} = b_{0} \\ D_{x} = b_{1} F_{z}^{2} + b_{2} F_{z} \\ B_{x} = \frac{(b_{3} F_{z}^{2} + b_{4} F_{z}) e^{(- b_{5} F_{z})}}{CD} \\ E_{x} = b_{6} F_{z}^{2} + b_{7} F_{z} + b_{8} \end{matrix} \end{matrix}$ (11)

轮胎侧向力因子为:

$\begin{matrix} \{\begin{matrix} C_{y} = a_{0} \\ D_{y} = a_{1} F_{z}^{2} + a_{2} F_{z} \\ B_{y} = a_{3} \sin [2 \arctan (F_{z} / a_{4})] \cdot \\ (1 - a_{5} |γ|) / CD \\ E_{y} = a_{6} F_{z}^{2} + a_{7} F_{z} + a_{8} \end{matrix} \end{matrix}$ (12)

式中:Y为纵向力、侧向力或回正力矩; X为纵向滑移率λ 或轮胎侧偏角α ; S_H、S_V分别为水平、垂直偏移常数; V_rw为轮速ω 与轮胎有效半径r_w的乘积; V_x_w、V_y_w分别为车轮中心的纵向、横向速度; B为刚度因子; C为形状因子; D为峰值因子; E为曲率因子; F_z为轮胎垂直载荷; a₀~a₈、b₀~b₈为拟合参数, 数值如表1所示。

表1 魔术公式轮胎模型参数(Michelin^© MXV8 205/55R16 91V) Table 1 Parameter values in magic formula(Michelin^© MXV8 205/55R16 91V)

考虑汽车在转弯、制动过程中的轮荷转移和轴荷转移效应, 对每个车轮的垂直载荷计算如下^[20]:

$\begin{matrix} \{\begin{matrix} F_{zfl} = (g \frac{b}{2} - a_{x} \frac{h}{2} - a_{y} \frac{bh}{c} + a_{x} a_{y} \frac{h^{2}}{gc}) \frac{m}{L} \\ F_{zfr} = (g \frac{b}{2} - a_{x} \frac{h}{2} + a_{y} \frac{bh}{c} - a_{x} a_{y} \frac{h^{2}}{gc}) \frac{m}{L} \\ F_{zrl} = (g \frac{a}{2} + a_{x} \frac{h}{2} - a_{y} \frac{ah}{c} - a_{x} a_{y} \frac{h^{2}}{gc}) \frac{m}{L} \\ F_{zrr} = (g \frac{a}{2} + a_{x} \frac{h}{2} + a_{y} \frac{ah}{c} + a_{x} a_{y} \frac{h^{2}}{gc}) \frac{m}{L} \end{matrix} \end{matrix}$ (13)

式中:a_x、a_y分别为汽车纵向、横向加速度; L为汽车轴距; h为汽车质心高度。

轮胎的纵向力与侧向力必须满足“ 附着椭圆” 的条件约束, 因此, 最终轮胎的纵向、侧向力表达式为:

σ _x=, σ _y= $\begin{matrix} \frac{tanα}{1 + λ} \end{matrix}$ (14)

σ = $\begin{matrix} \sqrt[]{δ_{x}^{2} + δ_{y}^{2}} \end{matrix}$ (15)

F_x= $\begin{matrix} \frac{|σ_{x}|}{σ} \end{matrix}$ Y(X), F_y= $\begin{matrix} \frac{|σ_{y}|}{σ} \end{matrix}$ Y(X)(16)

式中:F_x、F_y分别为修正后的轮胎纵向力、侧向力。

2.3 IEHB执行机构关键部件模型

2.3.1 电动主缸模型

本研究采用永磁同步电机(PMSM)作为电动主缸的动力控制源, 基于d、q坐标分解, PMSM的电压平衡方程可以描述为^[21]:

$\begin{matrix} \{\begin{matrix} u_{d} = R_{s} i_{d} + L_{s} \frac{d i_{d}}{dt} - ω_{r} L_{s} i_{q} \\ u_{q} = R_{s} i_{q} + L_{s} \frac{d i_{q}}{dt} + ω_{r} ψ_{r} + L_{s} ω_{r} i_{d} \end{matrix} \end{matrix}$ (17)

PMSM转矩方程为:

T_e=K_ti_q(18)

PMSM转子轴上的转矩平衡方程为:

J=T_e-T_L(19)

在矢量控制条件下, i_d≡ 0, PMSM的电压平衡方程和电磁转矩方程则化简为:

$\begin{matrix} \{\begin{matrix} u_{q} = R_{s} i_{q} + L_{s} \frac{d i_{q}}{dt} + ω_{r} ψ_{r} \\ T_{e} = K_{t} i_{q} \end{matrix} \end{matrix}$ (20)

电动主缸通过螺旋副传动机构将PMSM的旋转运动转换为主缸推杆的直线运动, 相关方程如下:

$\begin{matrix} \frac{θ_{T}}{2 π} \end{matrix}$ = $\begin{matrix} \frac{S}{L_{p}} \end{matrix}$ (21)

F_p=2π η $\begin{matrix} \frac{T_{D}}{L_{p}} \end{matrix}$ (22)

θ _M=θ _T, T_D=T_L(23)

以主缸中的两个活塞为研究对象, 建立主缸模型为:

M₂ $\begin{matrix} \frac{d^{2} S}{dt} \end{matrix}$ =F_p-A₂P₂-C₂-F_s2(24)

M₁ $\begin{matrix} \frac{d^{2} X_{1}}{dt} \end{matrix}$ =F_s2+A₂P₂-A₁P₁-C₁ $\begin{matrix} \frac{d X_{1}}{dt} \end{matrix}$ -F_s1(25)

F_s2=K₂(S-X₁), F_s1=K₁X₁(26)

式中:u_d、u_q分别为d、q轴的电压; i_d、i_q分别为d、q轴电流; R_s为定子电阻; L_s为定子电感; ω _r为电机转速; ψ _r为转子永磁体磁链; T_e为电磁转矩; K_t为电磁转矩系数; J为电机转子转动惯量; T_L为负载转矩; T_D为传动机构驱动转矩; L_p为螺旋副传动机构的导程; S为螺旋副传动机构输出的直线位移; F_p为螺旋副传动机构输出推力; θ _M为PMSM转子转角; η 为螺旋副传动机构的传动效率; θ _T为螺旋副传动机构输出转角; A₁、A₂分别为主缸前腔、后腔有效横截面积; M₁、M₂分别为主缸前活塞、后活塞质量; F_s1、F_s2分别为主缸前腔、后腔弹簧力; K₁、K₂分别为主缸前腔、后腔弹簧的刚度; C₁、C₂分别为主缸前腔、后腔活塞阻尼系数; P₁、P₂分别为主缸前腔、后腔压力; X₁为主缸前腔活塞位移。

2.3.2 电磁阀模型

为了有效地控制液压调节单元中的电磁阀, 采用调节脉宽占空比, 控制阀芯开度, 进而实现制动压力的精确调控。脉宽占空比表达式为:

τ = $\begin{matrix} \frac{T_{p}}{T} \end{matrix}$ (27)

本文以平均流量来研究电磁阀压力-流量特性, 数学模型如下:

= $\begin{matrix} \frac{T_{p}}{T} \end{matrix}$ q_Vn=τ C_dA_v $\begin{matrix} \sqrt[]{\frac{2}{ρ} Δp} \end{matrix}$ (28)

式中:T_p、T分别为有效脉宽时间、脉宽周期; τ 为占空比; 为平均流量; q_Vn为额度流量; C_d为流量系数; A_v为阀口横截面积; ρ 为油液密度; Δ p为电磁阀进、出口端压差。

2.3.3 制动轮缸模型

制动轮缸输出的制动力矩计算如下^[18]:

T_b_{_ij}=π k_bp_{b_}_ijr_ed²(29)

式中:k_b为制动系数; p_b_{_ij}为目标轮缸制动压力; r_e为制动压力有效作用半径; d为制动轮缸活塞直径。

3 轮胎滑移率控制器设计

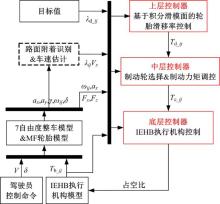
根据本文所建立的整车模型、轮胎模型、IEHB执行机构模型, 设计基于分层控制架构与双闭环非线性控制方法的轮胎滑移率控制器, 其控制架构如图3所示。

	Figure Option View Download New Window
	图3 基于IEHB系统的轮胎滑移率控制策略架构Fig.3 Structure of wheel slip control based on IEHB

3.1 上层控制策略

设k₁、k₂分别为滑模增益系数; λ _d为期望的轮胎滑移率; f为轮胎滚动阻力系数。针对制动过程中被控车辆和制动系统的非线性问题, 设计基于滑模变结构控制理论的轮胎滑移率上层控制器, 以汽车当前的滑移率与期望的滑移率之间的偏差为控制变量, 具体如下:

e_ij=λ _ij-λ _d_{_ij}(30)

为了保证消除稳态误差, 设计滑模面为:

S_f_{_ij}=e_ij+k₁∫ e_ijdt(31)

当S_f_{_ij}=0成立时, 对式(31)左右两边微分得:

$\begin{matrix} {\overset{\cdot}{S}}_{f_ij} \end{matrix}$ = $\begin{matrix} {\overset{\cdot}{e}}_{ij} \end{matrix}$ +k₁e_ij= $\begin{matrix} {\overset{\cdot}{λ}}_{ij} \end{matrix}$ - $\begin{matrix} {\overset{\cdot}{λ}}_{d_ij} \end{matrix}$ +k₁(λ _ij-λ _d_{_ij})=0(32)

根据式(8)得到滑移率的微分方程如下:

$\begin{matrix} {\overset{\cdot}{λ}}_{ij} \end{matrix}$ = $\begin{matrix} \frac{ω_{ij} r_{w} {\overset{\cdot}{v}}_{xw_ij}}{v_{xw_ij}^{2}} \end{matrix}$ - $\begin{matrix} \frac{{\overset{\cdot}{ω}}_{ij} r_{w}}{v_{xw_ij}} \end{matrix}$ (33)

根据单轮车辆模型及式(32)(33)可以推导出等效制动力矩, 表达式为:

T_{beq_}_ij=F_xr_w+ $\begin{matrix} {\overset{\cdot}{λ}}_{b_ij} \end{matrix} \begin{matrix} \frac{J_{w} v_{xw_ij}}{r_{w}} \end{matrix}$ -fF_{z_ij}r_w- $\begin{matrix} \frac{ω_{ij} J_{w} {\overset{\cdot}{v}}_{xw_ij}}{v_{xw_ij}} \end{matrix}$ - $\begin{matrix} \frac{k_{1} e_{ij} J_{w} v_{xw_ij}}{r_{w}} \end{matrix}$ (34)

为了使系统的状态在滑模面S_f=0附近滑动, 并保证系统的鲁棒性, 设计补偿制动控制力矩为:

T_bc_{_ij}=- $\begin{matrix} \frac{k_{2} v_{xw_ij} J_{w} sgn (S_{f_ij})}{r_{w}} \end{matrix}$ (35)

由于sgn(x)属于不连续函数, 所以控制时会产生很明显的抖颤效果, 所以在这里用tanh(x/n)双曲正切连续函数代替, 可有效地降低滑模控制中的抖振, 其中n> 0, 其大小决定了双曲正切光滑函数的拐点的快慢, 因此方程(35)变为:

T_bc_{_ij}=- $\begin{matrix} \frac{k_{2} v_{xw_ij} J_{w} \tanh (S_{f_ij} / n)}{r_{w}} \end{matrix}$ (36)

根据式(34)(36)可以得出总的理想制动控制力矩如下:

T_d_{_ij}=T_beq_{_ij}+T_bc_{_ij}(37)

3.2 中层控制策略

通过滑模控制器输出的目标制动控制力矩具有一定程度的抖颤, 致使控制超调, 进而导致制动车轮抱死, 因此, 需要对目标制动控制力矩进行修正。

当估算的制动轮纵向滑移率值小于λ _d(1+x_m)时, 车轮的修正制动控制力矩为:

T_c_{_ij}=0(38)

当估算的制动轮纵向滑移率值在[λ _d(1+x_m), λ _d(1-x_m)]区间时, 车轮的修正制动控制力矩为:

T_c_{_ij}=f(λ _ij)= $\begin{matrix} \frac{T_{d_ij}}{2 x} \end{matrix}$ (- $\begin{matrix} \frac{λ_{ij}}{λ_{d}} \end{matrix}$ +1+x_m)(39)

当估算的制动轮纵向滑移率值在[λ _d(1-x_m), 0]区间时, 车轮的修正制动控制力矩为:

T_c_{_ij}=T_d_{_ij}(40)

式中:x_m为滑移率调控裕度。

3.3 底层控制策略

IEHB 执行机构的液压制动力是通过电动主缸及液压调节单元(电磁阀和回油泵)的触发模式调控的。本文所设计的执行层控制策略如表2所示。

表2 IEHB执行机构控制策略 Table 2 Control strategy of IEHB actuator

当系统增压控制时, 电动主缸的PMSM输入的控制扭矩为T_m, 进液阀的控制指令为0, 出液阀的控制指令为0, 回油泵的控制指令为0; 当系统保压控制时, PMSM输入的控制扭矩为0, 进液阀的控制指令为U_pc, 出液阀的控制指令为0, 回油泵的控制指令为0; 当系统减压控制时, PMSM输入的控制扭矩为T_m, 进液阀的控制指令为U_pc, 出液阀的控制指令为U_pc, 回油泵的控制指令为U_pc。

PMSM输入的控制扭矩T_m通过设计非线性控制器确定, 具体如下:

T_m=k_m∑ tanh(T_b_{_ij}-T_c_{_ij})(41)

考虑电动主缸的实际执行能力, 对控制扭矩T_m设计如下约束条件:

-0.2 N· m≤ T_m≤ 1.5 N· m(42)

控制指令U_pc由液压控制逆向模型确定, 其表达为^[22]:

U_pc= $\begin{matrix} \frac{P_{b} - P_{w}}{(x_{1} + x_{2} P_{w}) \sqrt[]{|P_{M} - P_{w}|}} \end{matrix}$ (43)

式中:k_m为电机转矩控制系数; P_M为电动主缸输出压力; P_w为当前时刻轮缸制动压力; x₁、x₂分别为最小二乘法拟合得到的参数。

4 仿真试验

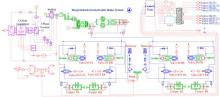
为了验证基于集成式线控液压制动系统的轮胎滑移率控制策略的控制效果, 本研究通过MATLAB/Simulink与AMESim联合仿真平台, 分别在高附着路面和低附着路面进行仿真试验, 搭建的IEHB执行机构物理仿真模型如图4所示, 并且关键参数见文献[23]。整车动力学模型参数详见表3。

通过对水平、均匀、公共道路的路面上测量得到的“ 附着率-滑移率” 关系曲线分析, 现代轮胎在高、低附着路面上的最佳附着率一般对应的滑移率在0.1左右^[24], 同时考虑汽车制动过程中侧向稳定性及载荷转移等问题, 所以本文设置车辆前轴和后轴理想滑移率λ _d分别为0.1和0.08, 滑移率调控裕度x_m分别为10%和5%。

	Figure Option View Download New Window
	图4 IEHB执行机构物理仿真模型Fig.4 Physical simulation model of IEHB actuator

表3 整车模型参数 Table 3 Parameters of vehicle model

4.1 高附着路面上主动紧急制动仿真试验

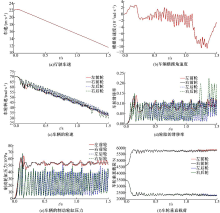
设置仿真试验在路面附着系数为0.8的路面上进行, 初始车速v=80 km/h, 无方向盘转角输入。此时, 在IEHB控制系统的作用下车辆开始主动紧急制动。

由图5(a)(b)可见, 车辆在高附着路面高速主动紧急制动过程中, 汽车行驶车速在1.5 s内从22.22 m/s下降到11.57 m/s, 车速与时间有较好的线性关系, 变化平稳; 汽车横摆角速度峰值为0.01 rad/s, 保证了车辆在高速紧急制动时的侧向稳定性。通过图5(c)(d)(e)可知, 在IEHB系统控制下, 不仅能够防止汽车前、后轴车轮抱死, 同时还能够使其较好地跟踪目标滑移率, 前轴最大跟踪误差为0.039, 后轴最大跟踪误差为0.142, 前、后制动轮缸平均压力大致为5.36 MPa和2.53 MPa。对图5(f)分析可知, 在高附着路面高速主动紧急制动工况下, 汽车轴荷转移大致为3500 N, 且由于制动过程中产生了微小侧向扰动, 致使右后车轮比其他车轮更容易抱死, 滑移率也更难控制一些。

	Figure Option View Download New Window
	图5 高附着路面上主动紧急制动仿真试验Fig.5 Simulation test during active emergency braking process on high adhesion coefficient road

4.2 低附着路面上主动紧急制动仿真试验

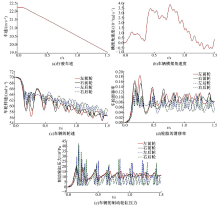
设置仿真试验在路面附着系数为0.2的路面上进行, 初始车速v=80 km/h, 无方向盘转角输入。此时, 在IEHB控制系统的作用下车辆开始主动紧急制动。

由图6(a)(b)可见, 车辆在低附着路面高速主动紧急制动过程中, 汽车行驶车速在1.5 s内从22.22 m/s下降到19.54 m/s, 车速与时间有较好的线性关系, 变化平稳; 汽车横摆角速度峰值为3.82× 10^-3rad/s, 保证了车辆在高速紧急制动时的侧向稳定性。通过图6(c)(d)(e)可知, 在IEHB系统控制下, 不仅能够防止汽车前、后轴车轮抱死, 同时还能够使其较好地跟踪目标滑移率, 前轴最大跟踪误差为0.084, 后轴最大跟踪误差为0.046, 前、后轴制动轮缸平均压力大致为1.15 MPa和0.75 MPa。

	Figure Option View Download New Window
	图6 低附着路面上主动紧急制动仿真试验Fig.6 Simulation test during active emergency braking process on low adhesion coefficient road

5 结束语

针对机电液系统本身的非线性问题, 实现基于IEHB系统的轮胎滑移率控制, 在建立IEHB执行机构物理仿真模型与7自由度整车动力学模型的基础上, 利用滑移率与制动转矩构成的双闭环非线性控制方法, 并结合分层控制构架, 设计了车轮滑移率控制器。通过MATLAB/Simulink与AMESim联合仿真平台, 分别在高附着、低附着路面进行了高速主动紧急制动仿真试验, 结果表明轮胎滑移率能够较好地跟踪目标滑移率, 提高了汽车的主动安全性能, 验证了本文所提出的基于IEHB系统的轮胎滑移率控制策略的有效性。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Clarke P, Muneer T, Cullinane K. Cutting vehicle emissions with regenerative braking[J]. Transportation Research Part D: Transport and Environment, 2010, 15(3): 160-167. [本文引用:1]
[2]	Gerla M, Lee E K, Pau G, et al. Internet of vehicles: from intelligent grid to autonomous cars and vehicular clouds[C]∥2014 IEEE World Forum on Internet of Things (WF-IoT), IEEE, 2014: 241-246. [本文引用:1]
[3]	Finn A, Scheding S. Developments and Challenges for Autonomous Unmanned Vehicles[M]. Berlin: Springer-Verlag, 2012. [本文引用:1]
[4]	王治中, 于良耀, 王语风, 等. 分布式电液制动系统执行机构液压控制[J]. 清华大学学报: 自然科学版, 2013, 53(10): 1464-1469. Wang Zhi-zhong, Yu Liang-yao, Wang Yu-feng, et al. Actuator pressure controller for a distributed electro-hydraulic braking system[J]. Journal of Tsinghua University(Science and Technology), 2013, 53(10): 1464-1469. [本文引用:1]
[5]	von Albrichsfeld C, Karner J. Brake system for hybrid and electric vehicles[C]∥SAE Technical Paper, 2009. [本文引用:1]
[6]	Jo C, Hwang S, Kim H. Clamping-force control for electromechanical brake[J]. IEEE Transactions on Vehicular Technology, 2010, 59(7): 3205-3212. [本文引用:1]
[7]	Jonner W D, Winner H, Dreilich L, et al. Electrohydraulic brake system-the first approach to brake-by-wire technology[C]∥SAE Technical Paper, 1996. [本文引用:1]
[8]	Soga M, Shimada M, Sakamoto J I, et al. Development of vehicle dynamics management system for hybrid vehicles: ECB system for improved environmental and vehicle dynamic performance[J]. JSAE Review, 2002, 23(4): 459-464. [本文引用:1]
[9]	Semmler S, Isermann R, Schwarz R, et al. Wheel slip control for antilock braking systems using brake-by-wire actuators[C]∥SAE Technical Paper, 2003. [本文引用:1]
[10]	Hong D, Hwang I, Yoon P, et al. Development of a vehicle stability control system using brake-by-wire actuators[J]. Journal of Dynamic Systems, Measurement, and Control, 2008, 130(1): 011008. [本文引用:1]
[11]	李寿涛, 马用学, 郭鹏程, 等. 一种变逻辑门限值的车辆稳定性控制策略研究[J]. 汽车工程, 2015, 37(7): 782-787. Li Shou-tao, Ma Yong-xue, Guo Peng-cheng, et al. A study on vehicle stability control strategy with variable threshold[J]. Automotive Engineering, 2015, 37(7): 782-787. [本文引用:1]
[12]	王建强, 王海鹏, 张磊. 基于电控液压制动装置的车辆主动报警/避撞系统[J]. 吉林大学学报: 工学版, 2012, 42(4): 816-822. Wang Jian-qiang, Wang Hai-peng, Zhang Lei. Vehicle collision warning and avoidance system based on electronic hydraulic brake device[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(4): 816-822. [本文引用:1]
[13]	王治中, 于良耀, 宋健. 基于制动系统的汽车车轮滑移率控制研究现状[J]. 汽车工程, 2014, 36(1): 81-87. Wang Zhi-zhong, Yu Liang-yao, Song Jian. The status quo of research on vehicle wheel slip control based on brake system[J]. Automotive Engineering, 2014, 36(1): 81-87. [本文引用:2]
[14]	余卓平, 徐松云, 熊璐, 等. 集成式电子液压制动系统鲁棒性液压力控制[J]. 机械工程学报, 2015, 51(16): 22-28. Yu Zhuo-ping, Xu Song-yun, Xiong Lu, et al. Robustness hydraulic pressure control system of integrated-electro-hydraulic brake system[J]. Journal of Mechanical Engineering, 2015, 51(16): 22-28. [本文引用:1]
[15]	Li J, Yang X, Miao H, et al. Co-simulation research of integrated electro-hydraulic braking system[C]∥SAE Technical Paper, 2016. [本文引用:1]
[16]	熊璐, 徐松云, 余卓平. 基于颤振补偿的电子液压制动系统液压力优化控制[J]. 机械工程学报, 2016, 52(12): 100-106. Xiong Lu, Xu Song-yun, Yu Zhuo-ping. Optimization of hydraulic pressure control system of integrated electro-hydraulic brake system based on chatter-compensation[J]. Journal of Mechanical Engineering, 2016, 52(12): 100-106. [本文引用:1]
[17]	Yang I J, Choi K, Huh K. Development of an electric booster system using sliding mode control for improved braking performance[J]. International Journal of Automotive Technology, 2012, 13(6): 1005-1011. [本文引用:1]
[18]	Li L, Jia G, Chen J, et al. A novel vehicle dynamics stability control algorithm based on the hierarchical strategy with constrain of nonlinear tyre forces[J]. Vehicle System Dynamics, 2015, 53(8): 1093-1116. [本文引用:2]
[19]	Pacejka H B, Bakker E. The magic formula tyre model[J]. Vehicle System Dynamics, 1992, 21(Sup. 1): 1-18. [本文引用:1]
[20]	Doumiati M, Victorino A, Lechner D, et al. Observers for vehicle tyre/road forces estimation: experimental validation[J]. Vehicle System Dynamics, 2010, 48(11): 1345-1378. [本文引用:1]
[21]	张晓光, 孙力, 赵克. 基于负载转矩滑模观测的永磁同步电机滑模控制[J]. 中国电机工程学报, 2012, 32(3): 111-116. Zhang Xiao-guang, Sun Li, Zhao Ke. Sliding mode control of PMSM based on a novel load torque sliding mode observer[J]. Proceedings of the CSEE, 2012, 32(3): 111-116. [本文引用:1]
[22]	van Zanten A T, Erhardt R, Pfaff G, et al. Control aspects of the Bosch-VDC[C]∥Proceedings of AVEC, Aachen, Germany, 1996: 573-608. [本文引用:1]
[23]	He X, Yang K, Ji X, et al. Research on vehicle stability control strategy based on integrated-electro-hydraulic brake system[C]∥SAE Technical Paper, 2017. [本文引用:1]
[24]	米克奇, 瓦伦托维兹. 汽车动力学[M]. 余强, 译. 4版. 北京: 清华大学出版社, 2009: 13-17. [本文引用:1]

2010

0.0

... 0 引言随着能源、环境、行车安全、交通拥堵等问题的日益突出,智能电动汽车逐渐成为热门话题,同时也对车辆底盘控制系统提出了更高的要求^[1,2,3] ...

2014

0.0

2012

0.0

2013

0.0

. 2013, 53(10):1464-1469

Actuator pressure controller for a distributed electro-hydraulic braking system

分布式电液制动系统执行机构液压控制

Wang Zhi-zhong , Yu Liang-yao , Wang Yu-feng

王治中, 于良耀, 王语风

... 二是线控机械制动系统,对传统汽车制动系统进行彻底革新,每个车轮配备一套电控制动执行机构^[4,5,6] ...

2009

0.0

... 二是线控机械制动系统,对传统汽车制动系统进行彻底革新,每个车轮配备一套电控制动执行机构^[4,5,6] ...

2010

0.0

... 二是线控机械制动系统,对传统汽车制动系统进行彻底革新,每个车轮配备一套电控制动执行机构^[4,5,6] ...

1996

0.0

... 博世公司在1996年发表了最早的相关研究论文^[7],丰田首先将EHB系统投入使用^[8] ...

2002

0.0

... 博世公司在1996年发表了最早的相关研究论文^[7],丰田首先将EHB系统投入使用^[8] ...

2003

0.0

... 而达姆施塔特技术大学、汉阳大学、吉林大学、清华大学等科研机构均对EHB系统控制进行了大量的研究工作^{[9,10,11,12,13]} ...

2008

0.0

... 而达姆施塔特技术大学、汉阳大学、吉林大学、清华大学等科研机构均对EHB系统控制进行了大量的研究工作^{[9,10,11,12,13]} ...

2015

0.0

. 2015, 37(7):782-787

A study on vehicle stability control strategy with variable threshold

一种变逻辑门限值的车辆稳定性控制策略研究

Li Shou-tao , Ma Yong-xue , Guo Peng-cheng

李寿涛, 马用学, 郭鹏程

... 而达姆施塔特技术大学、汉阳大学、吉林大学、清华大学等科研机构均对EHB系统控制进行了大量的研究工作^{[9,10,11,12,13]} ...

2012

0.0

. 2012, 42(4):816-822

Vehicle collision warning and avoidance system based on electronic hydraulic brake device

基于电控液压制动装置的车辆主动报警/避撞系统

Wang Jian-qiang , Wang Hai-peng , Zhang Lei.

王建强, 王海鹏, 张磊

A forward vehicle collision warning and avoidance system was proposed based on the electronic hydraulic brake device to prevent the rear-end collision. The system real-timely judges the dangerous level of rear-end collision with a time-to-collision algorithm based on the running situations of the front vehicle and this vehicle. When the collision possibility is detected, the system warns the driver with vision and hearing warnings and achieves the vehicle active collision avoidance by the electronic hydraulic brake. An experiment platform was established on a real vehicle to verify the brake pressure control effect. Introducing the system in a test vehicle, the test results show that the system provided timely the stepped collision warning and the brake assistance, enhancing the vehicle driving safety.

为预防道路尾随相撞事故,开发了一种基于电控液压制动装置的车辆前向报警/避撞系统。该系统根据前方车辆和自车的运动状态,基于碰撞时间实时判断尾随相撞危险度。在危险情况下,系统通过视听觉报警为驾驶员提供警示,并以电控液压制动的方式实现车辆的主动避撞。利用电控液压制动装置搭建了实验平台,对制动压力控制效果进行了验证。将系统安装于试验样车,实车试验结果表明,该系统能为驾驶员提供分级碰撞报警警示和制动辅助,以提高行车安全性。

... 而达姆施塔特技术大学、汉阳大学、吉林大学、清华大学等科研机构均对EHB系统控制进行了大量的研究工作^{[9,10,11,12,13]} ...

2014

0.0

. 2014, 36(1):81-87 DOI:doi:10.3969/j.issn.1000-680X.2014.01.019

The status quo of research on vehicle wheel slip control based on brake system

基于制动系统的汽车车轮滑移率控制研究现状

Wang Zhi-zhong , Yu Liang-yao , Song Jian.

王治中, 于良耀, 宋健

在分析了轮胎滑移率控制在汽车动力学控制中的作用,指出了被控车辆的非线性和时变性及其制动系统的非连续性和滞后是造成滑移率控制困难的主要原因的基础上,从制动系统、控制方法和研究手段3个方面概述了基于制动系统的轮胎滑移率控制研究现状,并提出了未来滑移率控制研究的主要方向.

... 而达姆施塔特技术大学、汉阳大学、吉林大学、清华大学等科研机构均对EHB系统控制进行了大量的研究工作^{[9,10,11,12,13]} ...

... 但机电液系统本身的非连续性和滞后性致使传统汽车制动系统很少以轮胎滑移率为直接控制目标^[13] ...

2015

0.0

. 2015, 51(16):22-28 DOI:doi:10.3901/JME.2015.16.022

Robustness hydraulic pressure control system of integrated-electro-hydraulic brake system

集成式电子液压制动系统鲁棒性液压力控制

Yu Zhuo-ping , Xu Song-yun , Xiong Lu

余卓平, 徐松云, 熊璐

摘　要：面向汽车集成式电子液压制动系统需求，设计一种鲁棒性液压力控制系统。基于系统特性分析发现，集成式电子液压制动系统为非线性时变系统，其工作受到温度、湿度、载荷扰动等多重不确定因素的影响，容易产生振荡的现象。因此要求液压力控制系统对外界不确定的扰动有较强的适应性，同时满足指标要求。利用基于系统改进的田口方法，提出一种集成式电子液压制动系统鲁棒性液压力控制方法。建立相关试验平台并利用该方法实现液压力鲁棒性控制。试验结果表明，所设计的鲁棒性液压力控制方法鲁棒性强，响应迅速，在500次试验内均保持稳健。因此，研究为非线性时变控制系统设计找到了一个新的设计方法，运用该方法设计出的控制系统可以使系统的输出对于干扰不敏感，在提高系统的鲁棒性的同时，优化系统性能。

... 作为一种新型的电子液压制动系统,集成式线控液压制动系统(Integrated-electro-hydraulic brake, IEHB)系统的伺服电动增压装置与主缸集成在一起,在保证整体结构紧凑的同时,通过联合液压调节单元,能够快速、准确地调节输出制动压力,所以IEHB可以更好地集成ABS(Anti-lock braking system)、ESP(Electronic stability program)、RBS(Regenerative braking system)、ACC(Adaptive cruise control)、AEB(Autonomous emergency braking)等整车控制功能^[14] ...

2016

0.0

... Li等^[15]通过 MATLAB/Simulink 与 CarSim 联合仿真的方法,对IEHB 执行机构的关键参数进行了分析,并对整车运动控制问题进行了研究 ...

2016

0.0

. 2016, 52(12):100-106 DOI:doi:10.3901/JME.2016.12.100

Optimization of hydraulic pressure control system of integrated electro-hydraulic brake system based on chatter-compensation

基于颤振补偿的电子液压制动系统液压力优化控制

Xiong Lu , Xu Song-yun , Yu Zhuo-ping.

熊璐, 徐松云, 余卓平

集成式电子液压制动系统满足了车辆智能化和电动化的发展需求,已经成为制动系统的发展趋势。针对集成式电子液压制动系统液压力控制中摩擦力给系统带来的振荡和低速爬行现象,采用颤振补偿方法对系统进行液压力控制。试验表明,叠加颤振信号后的系统控制精度高,系统性能得到改善。在跟踪正弦信号时,相对于无颤振补偿的系统其误差方均根减小了79.7%。针对颤振补偿,基于试验分析,对比不同的颤振补偿信号的响应,从而优化了低频和高频液压力控制工况下叠加的颤振信号。试验证明,颤振补偿能够减轻集成式电子液压制动系统液压力控制中摩擦力所带来的振荡和低速爬行现象。此外,经过优化的颤振信号能够进一步地提高系统的液压力控制品质。

... 熊璐等^[16]通过IEHB系统特性分析,利用颤振补偿方法对IEHB系统进行液压力优化控制研究 ...

2012

0.0

... Yang^[17]等针对IEHB的伺服电动建压装置利用 Lyapunov 函数设计了滑模控制器,并与传统 PID 控制器的控制效果进行了对比 ...

2015

0.0

... 1 整车动力学模型在轮胎滑移率控制器设计过程中,需要考虑车辆车轮的运动状态、各车轮垂向载荷的变化及制动时汽车的方向稳定性,因此选择建立7自由度车辆模型(见图2),动力学方程描述为^[18]: ...

... 制动轮缸输出的制动力矩计算如下^[18]: ...

1992

0.0

... 2 非线性轮胎模型为了反映真实的轮胎动力学特性,本文采用Pacejka魔术公式描述轮胎的非线性动力学行为^[19],其统一表达式如下: ...

2010

0.0

... 考虑汽车在转弯、制动过程中的轮荷转移和轴荷转移效应,对每个车轮的垂直载荷计算如下^[20]: ...

2012

0.0

. 2012, 32(3):111-116

Sliding mode control of PMSM based on a novel load torque sliding mode observer

基于负载转矩滑模观测的永磁同步电机滑模控制

Zhang Xiao-guang , Sun Li , Zhao Ke.

张晓光, 孙力, 赵克

An extended sliding-mode observer of the load torque was proposed, of which the state variables were speed and load torque, in order to decrease influence of varying load torque in a permanent magnet synchronous motor (PMSM) control system. Errors between the real and the observed speed were selected as a sliding-mode hyper plane, and the observed load torque was composed of a real load torque and the filtered chattering signal. The observation error converged to zero when sliding mode occurred. A sliding-mode variable structure control (SMC) .system of PMSM was designed based on the exponent reaching law, in which the observed load torque was used for feed-forward compensation. Experimental results show that the novel sliding-mode observer can estimate the load torque precisely, and the designed controller can enhance system robustness and suppress the intrinsic chattering of SMC.

为了减小负载转矩扰动对永磁同步电机(permanent magnet synchronous motor，PMSM)控制系统的影响，提高系统抗扰能力，提出一种以转速和负载转矩为观测对象的扩展滑模观测器，以实际转速与观测转速之差构成滑模面，负载转矩观测结果由负载转矩实际值和经过滤波后的抖振信号组成，当滑模运动发生后转矩观测误差渐进收敛到零。设计了基于指数趋近律的PMSM滑模控制(sliding-mode variable structure control，SMC)系统，将观测的负载转矩进行前馈补偿，以克服负载时变对控制性能的影响。实验结果表明，该观测器可准确地观测负载转矩，采用的前馈补偿方案对系统负载扰动有较强的鲁棒性，并且SMC固有抖振现象得到了有效抑制。

... 本研究采用永磁同步电机(PMSM)作为电动主缸的动力控制源,基于d、q坐标分解,PMSM的电压平衡方程可以描述为^[21]: ...

1996

0.0

... 控制指令U_pc由液压控制逆向模型确定,其表达为^[22]: ...

2017

0.0

2009

0.0

... 1左右^[24],同时考虑汽车制动过程中侧向稳定性及载荷转移等问题,所以本文设置车辆前轴和后轴理想滑移率#cod#x003bb ...