基于非线性模型的磁流变半主动悬架驱动系统

引用本文

李静, 韩佐悦, 杨威, 邢国成, 周瑜. 基于非线性模型的磁流变半主动悬架驱动系统[J].吉林大学学报（工学版）, 2018,48(3): 645-651
LI Jing, HAN Zuo-yue, YANG Wei, XING Guo-cheng, ZHOU Yu. Drive system for magnetorheological suspension based on nonlinear damper electric model[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 645-651 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170086
Permissions

基于非线性模型的磁流变半主动悬架驱动系统

李静, 韩佐悦, 杨威, 邢国成, 周瑜

吉林大学汽车仿真与控制国家重点实验室,长春 130022

作者简介:李静(1974-),男,教授,博士生导师.研究方向:汽车地面力分析与控制.E-mail:liye1129@163.com

基金:国家自然科学基金项目(51275206).

摘要

针对当前磁流变减振器电气模型不能很好地拟合减振器响应特性的问题,提出了基于自研磁流变减振器特性的非线性二级线圈电路模型,并基于减振器方波响应测试结果,采用遗传算法进行参数辨识。在此基础上,通过对电路及减振器传递函数的分析,提出了由单片机控制的可变结构驱动器方案,并设计了自抗扰控制器。通过硬件在环试验证明:相比PID控制的BUCK电路,本文设计的驱动器及控制器可以很好地提高磁流变减振器的响应速度。

关键词: 车辆工程; 磁流变; 非线性; 电流驱动器; 自抗扰控制器

中图分类号:U463.3 文献标志码:A 文章编号:1671-5497(2018)03-0645-07

Drive system for magnetorheological suspension based on nonlinear damper electric model

LI Jing, HAN Zuo-yue, YANG Wei, XING Guo-cheng, ZHOU Yu

State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

Abstract

To solve the issue of poor performance of present magnetorheological damper electric model for response characteristics, a nonlinear secondary coil model is put forward based on self-design damper. The model parameters are identified with GA algorithm based on square-wave test result. The transfer function of the circuit and damper model is analyzed and a current driver with variable structure is designed. An ADRC controller is designed for the current driver. HIL test results show that, compared with PID algorithm and BUCK circuit, the designed current driver and ADRC controller can improve the response characteristics of magnetorheological damper.

Keyword: vehicle engineering; magnetorheological; nonlinear; current driver; active disturbance rejection controller(ADRC)

文章图片

0 引言

磁流变减振器(Magnetorheological damper, MRD)由于其响应快、可控性强, 近年来逐渐发展成为半主动悬架的主要执行器类型之一, 而影响磁流变半主动悬架响应时间的主要因素是减振器线圈及驱动电路特性对减振器跟随目标电流能力的限制^[1]。因此, 国内、外学者对减振器响应特性建模及驱动器设计进行了大量研究。

Strecker等^[2]创建了一个电感串联线圈电阻及开关电阻的线性减振器线性模型, Goɬ dasz等^[3]针对减振器电流下降过程提出了一种二级互感线圈模型, 以上模型均为线性参数模型, 对于磁流变减振器中的高度非线性特性拟合效果并不理想。Jiang^[4]提出了一个时变方程来配合涡流产生的非线性影响, 但该模型需基于磁场有限元仿真获得感应电流。

磁流变减振器驱动方面, Yang等^[5]最早提出使用电流驱动器来降低线圈的响应时间; Koo等^[6]采用运算放大器比较电路及功率晶体管电路进行直接驱动及控制; Strecker等^[2]则采用场效应管直接进行驱动, 以上方案均使用简单的通断控制, 无滤波稳流措施, 电流波动严重。因此, 近年来大量国内、外学者借鉴直流开关电源中的BUCK电路进行电流驱动器的设计^{[7, 8, 9]}, BUCK电路通过电感和电容组成低通滤波, 实现了对减振器的近似恒流的输出, 有效降低了电路电流的波动, 但在动态响应上面仍有一定的不足。

在电流驱动器控制方面, 目前主要有基于模拟电路原理的负反馈控制^{[2, 7]}以及简单的PID^{[3, 8]}控制或PI^[5]控制。负反馈控制基于电路结构, 并不能很好地快速响应; 而简单PID控制的控制效果对控制参数匹配的依赖性较高, 适应性不好。

针对以上问题, 本文提出一种非线性二级线圈电路模型, 并基于自研减振器的方波响应测试数据, 采用改进的遗传算法进行参数辨识。通过对电路及减振器传递函数的分析, 提出变结构电流驱动器方案, 并使用自抗扰控制算法进行控制, 提高电流驱动器的适应性及抗干扰能力。最后, 通过硬件在环试验验证了所设计的电流驱动器对减振器响应特性的提升效果。

1 非线性二级线圈电路模型

1.1 非线性等效电路模型的提出

磁流变减振器的电流响应会受到减振器内部磁场变化、涡流效应的影响, 而磁流变液以及铁磁材料的磁化特性具有非常强的非线性特征, 因此线性电感及电阻组成的模型仅能模拟电流上升时的大致变化趋势却无法同时准确拟合小电流阶段和大电流阶段。而减振器电流下降阶段的能量耗散趋势可使用二级互感线圈模型进行近似描述。

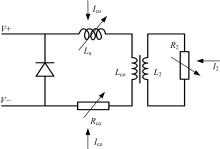
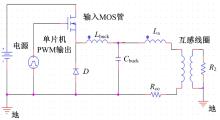
本文综合线性模型及二级互感线圈模型的特点, 提出了磁流变减振器非线性二级互感线圈模型, 如图1所示。

	Figure Option View Download New Window
	图1 MRD非线性二级互感线圈电路模型Fig.1 Nonlinear mutual inductor electric model for MRD

模型中L_co与L₂组成一对互感线圈, 附加电感L_a、电阻R_co随电流i_co发生参数变化并与线圈电感L_co串联组成一级回路; 线圈电感L₂与随感应电流i₂变化的电阻R₂串联组成二级回路, 在L_a与R_co两端并联有续流二极管, 形成减振器耗能回路。

模型中的L_a、R_co、R₂分别引入非线性特性:

$\begin{array}{l} L_{a} = L_{a 0} + L_{a 1} I_{co} + L_{a 2} I_{co}^{2} (1) \\ R_{co} = R_{co 0} + R_{co 1} I_{co} + R_{co 2} I_{co}^{2} (2) \\ R_{2} = R_{20} + R_{21} I_{2} + R_{22} I_{2}^{2} (3) \end{array}$

式中:L_a0、L_a1、L_a2分别为一级回路中附加电感的常数项、一次项系数以及二次项系数; R_co0、R_co1、R_co2分别为一级回路可变电阻的常数项、一次项系数以及二次项系数; R₂₀、R₂₁、R₂₂分别为二级回路电阻的常数项、一次项系数以及二次项系数。

由基尔霍夫定律拉氏变换获得模型系统方程:

$\begin{array}{l} R_{22} I_{2}^{3} + R_{21} I_{2}^{2} + (L_{2} s + R_{20}) I_{2} = K I_{co} s \sqrt{L_{co} L_{2}} \\ (L_{a 2} s + R_{co 2}) I_{co}^{3} + (L_{a 1} s + R_{co 1}) I_{co}^{2} + \\ (L_{a 0} s + L_{co} s + R_{co 0}) I_{co} + K I_{2} s \sqrt{L_{co} L_{2}} = U_{in} \end{array} (4)$

式中: $K$ 为线圈互感系数; U_in为减振器输入电压, 当减振器处于电流下降阶段, U_in=0, I_co(0)=0, I₂(0)=0。

由于状态方程中存在电流I_co、I₂的三次方项, 很难直接获得线圈电流响应的解析解, 但可以通过搭建模型进行数值计算。

1.2 减振器电路模型的参数辨识

提出的减振器模型中共有12个参数, 需针对目标减振器响应特性进行参数辨识。磁流变减振器在系统工作中接收以控制步长为周期的恒定电压输入, 因此选择方波电压输入作为典型工况进行辨识。

测试电路使用可控稳压直流电源控制减振器输入电压, 使用L298桥电路接收信号发生器的方波信号控制电路的通断, 使用712电流采集模块采集减振器的实际电流并放大输出。

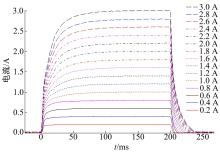
测试中方波周期为400 ms, 占空比为50%, 低电平为0 V, 高电平产生的减振器电流为0.2~3 A, 测试获得的减振器电流响应数据如图2所示。

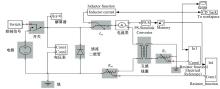
	Figure Option View Download New Window
	图2 MRD方波测试数据Fig.2 Square-wave test data for MRD

使用Matlab/Simulink中Simscape元件库依照测试电路搭建仿真模型, 如图3所示。

	Figure Option View Download New Window
	图3 MRD方波测试仿真模型Fig.3 Simulation model of square-wave test for MRD

参数辨识使用遗传算法, 种群数量为30, 优化代数为100, 交叉概率为0.5, 变异概率为0.05。优化对象为电流上升段(0~100 ms)及下降段(200~250 ms)内的仿真电流与试验结果的偏差。

适应度计算公式为:

$\begin{array}{l} f = e_{up} w_{up} + e_{down} = \\ w_{up} \int_{t_{up 0}}^{t_{up}} {(\frac{(I_{e} (i) - I_{s} (i)) I_{s} {(i)}^{2}}{I_{tar}})}^{2} + \\ \int_{t_{d 0}}^{t_{d}} {(\frac{I_{e} (i) - I_{s} (i)}{\max (0.1 I_{tar}, I_{e} (i))})}^{2} (5) \end{array}$

式中:e_up为电流上升段拟合偏差; e_down为电流下降段拟合偏差; I_e为试验数据; I_s为仿真数据; I_tar为高电平目标电流; w_up为依据初次拟合偏差设置的权重系数。

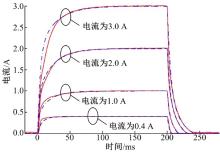
减振器常用工况(2.0 A电流方波输入)下的参数拟合结果如下所示:L_co=18.4820 mH; L₂=15.5355 mH; K=0.9255; R_co=1.4416 Ω ; R_co1=0.1118 Ω ; R_co2=0.0271 Ω ; L_a0=4.5883 mH; L_a1=1.6078 mH; L_a2=0.2151 mH; R₂₀=1.0000 Ω ; R₂₁=0.0863 Ω ; R₂₂=0.0671 Ω 。以相同方法进行其他输入下的参数拟合, 部分拟合结果如图4所示, 其中, 直线为试验值; 点划线为拟合值。

	Figure Option View Download New Window
	图4 参数拟合测试结果对比Fig.4 Test result comparison for parameter identification

使用拟合优度进行不同测试电流下的拟合结果评价, 结果如表1所示。

表1 电流方波测试拟合优度 Table 1 Goodness of fit for current square-wave test

从表1可以看出:除去电流为0.6 A以下测试的下降段拟合优度较低, 其他拟合优度均保持在0.88以上, 0.6 A以下下降时间拟合误差低于3.2 ms, 说明拟合数据可以很好地反映减振器响应特性。

2 电流驱动电路设计

现有基于BUCK电路的驱动器原理如图5所示。

	Figure Option View Download New Window
	图5 基于BUCK电路的驱动器电路Fig.5 Current driver based on BUCK circuit

该电路的系统方程为:

$\begin{array}{l} \{\begin{array}{l} U_{in} = L_{buck} \frac{d I_{1}}{d t} + U_{2} \\ I_{c} = C_{buck} \frac{d U_{2}}{d t} \\ U_{2} = I_{co} R_{co} + L_{a} \frac{d I_{co}}{d t} + L_{co} \frac{d I_{co}}{d t} + M \frac{d I_{2}}{d t} \\ I_{1} = I_{co} + I_{c} \\ 0 = I_{2} R_{2} + M \frac{d I_{co}}{d t} + L_{2} \frac{d I_{2}}{d t} \\ M = K \sqrt{L_{co} L_{2}} \end{array} \\ (6) \end{array}$

式中:L_buck、C_buck分别为BUCK电路中的电感值和电容值; $U_{2} 为减振器输入端电压值; M$ 为线圈互感。

求解系统传递函数, 得到系统特征方程为:

$\begin{array}{l} [(L_{a} + L_{co}) L_{2} - K^{2} L_{co} L_{2}] L_{buck} C_{buck} S^{4} + \\ [R_{co} L_{2} + (L_{a} + L_{co}) R_{2}] L_{buck} C_{buck} S^{3} + \\ [(L_{a} + L_{co}) L_{2} + L_{buck} C_{buck} R_{co} R_{2} + \\ L_{buck} L_{2} - K^{2} L_{co} L_{2}] S^{2} + \\ [R_{co} L_{2} + (L_{a} + L_{co}) R_{2} + L_{buck} R_{2}] S + R_{co} R_{2} = 0 (7) \end{array}$

由于电路中L_buck(0.01~0.1 mH)、C_buck(0.1~0.5 mF)^[15]明显小于磁流变减振器中器件参数1~2个数量级, 因此特征方程中L_buck、C_buck过小, 此处忽略不计, 系统传递函数简化为:

$\begin{array}{l} \frac{I_{co} (s)}{U_{PWM} (s)} = (L_{2} S + R_{2}) / {[(L_{a} + L_{co}) L_{2} + \\ L_{buck} L_{2} - K^{2} L_{co} L_{2}] S^{2} + [R_{co} L_{2} + (L_{a} + \\ L_{co}) R_{2} + L_{buck} R_{2}] S + R_{co} R_{2}} (8) \end{array}$

系统响应特性近似为有阻尼二阶系统, 系统固有频率为:

$ω_{n} = \sqrt{\frac{R_{co} R_{2}}{(L_{a} + L_{co}) L_{2} + L_{buck} L_{2} - K^{2} L_{co} L_{2}}} (9)$

系统相对阻尼比为:

$ζ = \frac{R_{co} L_{2} + (L_{a} + L_{co}) R_{2} + L_{buck} R_{2}}{2 \sqrt{R_{co} L_{2} R_{2} [L_{a} + L_{buck} + (1 - K^{2}) L_{co}]}} (10)$

在减振器工作过程中, 存在对系统阻尼比需求不同的两阶段:在控制目标变化时, 需系统相对阻尼比较小以提高电流对控制目标的响应; 在控制目标不变时, 需要系统相对阻尼比较大以维持系统输出稳定。

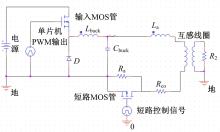
对系统阻尼比进行分析, 除L_buck参数影响较小外, 阻尼比随线圈互感 $M$ 的增大而增大, 由于R_coL₂明显小于(L_co+L_a)R₂, 增大R_co或L₂均可明显降低相对阻尼比。对于已设计好的减振器, $M$ 和L₂均已确定, 因此可以使用减振器串联电阻的方式增大R_co, 改变系统阻尼比, 配置出系统不同的动态响应特性。

基于以上分析及传统BUCK电路提出变结构方案, 如图6所示。

	Figure Option View Download New Window
	图6 提出的变结构电流驱动器方案Fig.6 Variable current driver scheme

该电流驱动器使用单片机PWM模块控制BUCK电路输入电压, BUCK电路输出连接减振器后与耗能电阻R_a相连, 耗能电阻R_a并联耗尽型MOS管, 稳态工作状态下, MOS管导通将耗能电阻短路, 系统保持大阻尼、低功耗状态, 当控制目标转变时, 断开MOS管, 降低系统阻尼比, 提高系统响应速度。

3 驱动系统控制算法设计

串联电阻的方式可以有效加快系统响应, 但该方法在电流上升段易造成电路驱动能力突变导致系统不稳定。电流上升段可以使用控制算法利用电源的驱动电压余量提升系统的响应速度。

在第1.2节模型参数辨识中不同工况下会存在一定的参数波动, 而传统PID控制参数对系统参数较为敏感, 也容易产生超调。针对以上问题, 采用韩京清院士^[10]提出的自抗扰控制方法(Active disturbonce rejection controller, ADRC)搭建控制器。

将系统状态方程改写为:

$\{\begin{array}{l} {\overset{\cdot}{x}}_{1} = x_{2} \\ {\overset{\cdot}{x}}_{2} = \frac{L_{2} {\overset{\cdot}{U}}_{in} + R_{2} U_{in} - B x_{2} - C x_{1}}{A} \\ y = x_{1} \end{array} (11)$

式中:A=(L_a+L_co)L₂+L_buckL₂-K²L_coL₂; B=R_coL₂+(L_a+L_co)R₂+L_buckR₂; C=R_coR₂; x₁=i_coil。

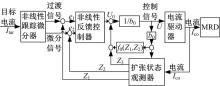
将式(11)中 $- \frac{B x_{2} + C x_{1}}{A}$ 作为系统已知部分; 将参数波动及拟合误差作为外部扰动; 将 $\frac{L_{2} {\overset{\cdot}{U}}_{in} + R_{2} U_{in}}{A}$ 作为系统输入。

采用二阶系统最速控制综合函数fhan构建非线性跟踪微分器; 采用非线性fal函数构建非线性扩张状态观测器, 观测器中引入系统已知部分以提高观测效果; 非线性反馈控制器使用偏差信号的非线性fal函数线性组合生成初级控制信号U₀, 引入系统扰动估计和系统模型估计线性组合生成最终控制信号U。搭建的自抗扰控制器如图7所示。

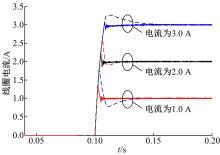
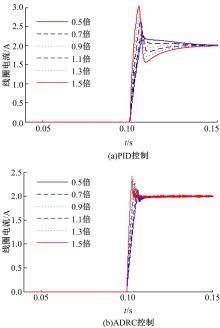
	Figure Option View Download New Window
	图7 自抗扰控制器结构框图Fig.7 Structure diagram of ADRC controller

使用传统PID控制和自抗扰控制器进行不同目标电流下的控制对比, 取PID参数K_p=12, K_d=0.07, K_i=1300, 对比结果如图8所示。

	Figure Option View Download New Window
	图8 不同目标电流下控制效果对比Fig.8 Control result comparison for variable target current

在2.0 A目标电流工况下, 将减振器参数进行± 50%的摄动, 控制效果对比如图9所示。

	Figure Option View Download New Window
	图9 不同参数摄动下控制效果对比Fig.9 Control result comparison for variable parameters

通过对比发现, 针对电流上升段, 在不同控制工况下及参数摄动下, 自抗扰控制具有比传统PID控制更稳定的控制效果和更小的超调量。

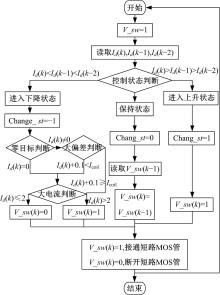
针对下降段的耗能电阻切换控制算法则要充分考虑状态切换条件, 避免在目标电流附近及控制目标缓慢变化时产生巨大波动, 同时防止剧烈放电造成元件烧毁, 电路切换控制算法结构如图10所示。

	Figure Option View Download New Window
	图10 电流驱动器电阻切换程序Fig.10 Resistor switching program of current driver

4 硬件在环试验

为了验证设计的电流驱动器性能, 使用以上设计的电流驱动器及控制算法进行悬架应用场景的电流跟随硬件在环试验, 硬件测试系统如图11所示。

	Figure Option View Download New Window
	图11 硬件在环测试系统Fig.11 Hardware-in-loop test system

使用1/4车辆悬架模型在C级路面, 车速为60 km/h工况下进行天棚阻尼控制仿真, 获取减振器控制电流数据作为硬件在环试验输入。

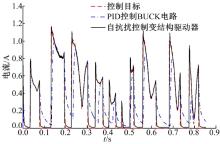
获得的控制电流数据由dSPACE/MicroAutobox以模拟电压信号输出给电流驱动器输入端, 由电流驱动器驱动磁流变减振器, 并通过采样电阻采集减振器实际电流。使用自抗扰控制器的变结构电流驱动器的电流跟随效果对比, 如图12所示。

	Figure Option View Download New Window
	图12 自抗扰控制变结构电流驱动器电流跟随效果Fig.12 Current following result of current driver with ADRC

试验结果表明:相比BUCK驱动电路, 电流驱动器可变结构的引入使得减振器实际电流在控制目标下降时可以更迅速跟随上目标电流。而对于控制目标上升阶段, 在相同的控制频率(10 kHz)下, 使用自抗扰控制的变结构电流驱动器可以有效减小减振器目标电流调节的响应时间并获得更好的目标跟随效果。虽然在目标电流突变时会产生少量的超调, 但处于电路安全使用范围内。

5 结论

(1)文本提出的非线性二级线圈电路模型可以有效模拟磁流变减振器在典型工作情况下的动态响应特性。

(2)减小线圈内部互感, 增大参数R_co或 $L_{2}$ 均可有效提高减振器驱动电路的响应速度。

(3)使用自抗扰控制算法控制电流驱动器相比传统PID可以有效抑制电流超调并减小系统参数波动造成的影响。

(4)硬件在环试验证明, 使用自抗扰控制变结构电流驱动器相比PID控制的BUCK电路可以更好地跟随目标电流, 更适用于磁流变半主动悬架。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Strecker Z, Roupec J, Mazurek I, et al. Limiting factors of the response time of the magnetorheological damper[J]. International Journal of Applied Electromagnetics & Mechanics, 2015, 47(2): 541-550. [本文引用:1]
[2]	Strecker Z, Roupec J, Mazurek I, et al. Design of magnetorheological damper with short time response[J]. Journal of Intelligent Material Systems & Structures, 2015, 26(14): 1951-1958. [本文引用:3]
[3]	Goɬdasz J, Sapiński B. Insight into Magnetorheological Shock Absorbers[M]. New York: Springer International Publishing, 2015. [本文引用:2]
[4]	Jiang Z S. Increasing resilience in civil structures using smart damping technology[D]. Connecticut: University of Connecticut, 2012. [本文引用:1]
[5]	Yang G, Jung H J, Spencer B F, et al. Dynamic modeling of large-scale magnetorheological damper systems for civil engineering applications[J]. Journal of Engineering Mechanics, 2004, 130(9): 1107-1114. [本文引用:2]
[6]	Koo J H, Goncalves F D, Ahmadian M. A comprehensive analysis of the response time of MR dampers[J]. Smart Materials & Structures, 2006, 15(2): 351-358. [本文引用:1]
[7]	石志涛, 张进秋, 岳杰, 等. 磁流变阻尼器的电流驱动器设计与实验研究[J]. 机械与电子, 2012(6): 18-20. Shi Zhi-tao, Zhang Jin-qiu, Yue Jie, et al. Study on design methodology of electric current driver for magneto-rheological fluid dampers[J]. Machinery & Electronics, 2012(6): 18-20. [本文引用:2]
[8]	周瑜. 某轿车车身姿态半主动悬架最优控制研究[D]. 长春: 吉林大学汽车工程学院, 2016. Zhou Yu. Research on the body attitude control of semi-active suspension vehicle using optimal control theory[D]. Changchun: College of Automotive Engineering, Jilin University, 2016. [本文引用:2]
[9]	Mohammad M N, Tadayoninejad A, Eghtesad M. An innovative design of fast current controller circuit foe MR dampers[J] . 2nd International Conference on Control, Instrumentation and Automation, Shiraz, 2011: 1086-1090. [本文引用:1]
[10]	韩京清. 自抗扰控制技术[J]. 前沿科学, 2007, 1(1): 24-31. Han Jing-qing, Auto disturbances rejection control technique[J]. Frontier Science, 2007, 1(1): 24-31. [本文引用:1]

2015

0.0

... 0 引言磁流变减振器(Magnetorheological damper,MRD)由于其响应快、可控性强,近年来逐渐发展成为半主动悬架的主要执行器类型之一,而影响磁流变半主动悬架响应时间的主要因素是减振器线圈及驱动电路特性对减振器跟随目标电流能力的限制^[1] ...

2015

0.0

... Strecker等^[2]创建了一个电感串联线圈电阻及开关电阻的线性减振器线性模型,Go#cod#x0026c ...

... Strecker等^[2]则采用场效应管直接进行驱动,以上方案均使用简单的通断控制,无滤波稳流措施,电流波动严重 ...

... 在电流驱动器控制方面,目前主要有基于模拟电路原理的负反馈控制^[2,7]以及简单的PID^[3,8]控制或PI^[5]控制 ...

2015

0.0

... dasz等^[3]针对减振器电流下降过程提出了一种二级互感线圈模型,以上模型均为线性参数模型,对于磁流变减振器中的高度非线性特性拟合效果并不理想 ...

... 在电流驱动器控制方面,目前主要有基于模拟电路原理的负反馈控制^[2,7]以及简单的PID^[3,8]控制或PI^[5]控制 ...

2012

0.0

... Jiang^[4]提出了一个时变方程来配合涡流产生的非线性影响,但该模型需基于磁场有限元仿真获得感应电流 ...

2004

0.0

... 磁流变减振器驱动方面,Yang等^[5]最早提出使用电流驱动器来降低线圈的响应时间 ...

... 在电流驱动器控制方面,目前主要有基于模拟电路原理的负反馈控制^[2,7]以及简单的PID^[3,8]控制或PI^[5]控制 ...

2006

0.0

... Koo等^[6]采用运算放大器比较电路及功率晶体管电路进行直接驱动及控制 ...

2012

0.0

. 2012, (6):18-20 DOI:doi:10.3969/j.issn.1001-2257.2012.06.005

Study on design methodology of electric current driver for magneto-rheological fluid dampers

磁流变阻尼器的电流驱动器设计与实验研究

Shi Zhi-tao , Zhang Jin-qiu , Yue Jie

石志涛, 张进秋, 岳杰

采用Buck型变换器和电流模式PWM开关控制方案,设计了车用磁流变阻尼器的电流驱动器,研究了其硬件电路组成,介绍了磁流变阻尼器的电流驱动器的性能测试系统并进行了测试实验.

... 因此,近年来大量国内、外学者借鉴直流开关电源中的BUCK电路进行电流驱动器的设计^[7,8,9],BUCK电路通过电感和电容组成低通滤波,实现了对减振器的近似恒流的输出,有效降低了电路电流的波动,但在动态响应上面仍有一定的不足 ...

... 在电流驱动器控制方面,目前主要有基于模拟电路原理的负反馈控制^[2,7]以及简单的PID^[3,8]控制或PI^[5]控制 ...

2016

0.0

. 2016, :-

Research on the body attitude control of semi-active suspension vehicle using optimal control theory

某轿车车身姿态半主动悬架最优控制研究

Zhou Yu

周瑜

悬架是影响汽车乘坐舒适性的重要部件,传统的被动悬架乘坐舒适性有限,且很难再有提升空间,而主动悬架功耗大、体积大、成本高,使其很难在轿车上普及,故近年来半主动悬架越来越受到车企的重视。本文以控制车身垂直、俯仰、侧倾三个方向上的姿态为目的,采用最优控制理论去研究实用有效的半主动悬架控制方法。具体研究内容如下:(1)查阅相关文献,对电控悬架用于车身姿态的控制、半主动悬架中阻尼可调减振器以及半主动悬架的控制方法进行了综述。(2)搭建1/4车辆模型和路面模型,并建立基于1/4车辆模型的半主动悬架线性二次型最优控制(LQR)模型进行仿真,分析最优控制中权重系数对车身质心垂直加速度、悬架动挠度和车轮动载荷三个指标的影响。(3)研究基于七自由度整车模型的LQR控制对车身姿态的控制,选取车身垂直加速度、俯仰角加速度和侧倾角加速度为控制目标计算性能指标。最优控制运用于实际需要知道车辆的全状态,如果这些状态中包含绝对位移或者绝对角度等难以精确测量的量就难以使用LQR控制。本文对被控模型的状态方程进行一阶求导,变形后的状态方程仍然符合最优控制的标准形式,新的状态方程再使用LQR控制能够避免使用绝对位移和绝对角度,同时使控制量变为控制增量。通过仿真分析出增量式的LQR控制具有良好的控制效果。最后,提出根据悬架变形量来自适应调整增量式LQR控制中的权重系数的控制方法。(4)利用能够提供精确整车模型的Car Sim软件,针对不同工况对改进的LQR控制作进一步验证。采用某实车的参数去设置整车模型。对实际的用于该车的磁流变减振器进行台架试验,根据试验数据搭建磁流变减振器的查表模型用于仿真,并搭建旋转拉伸曲面拟合的磁流变减振器的逆模型用于控制,逆模型根据理想阻尼力和减振器压缩速率计算磁流变减振器的控制电流。通过对比被动悬架和装有磁流变减振器的半主动悬架的仿真曲线,分析增量式LQR控制与自适应增量式LQR控制的控制效果。(5)为了分析自适应增量式LQR控制的实用性搭建控制器硬件在环试验台。硬件在环试验台主要包含上位机、d SPACE硬件板卡、集成了驱动器的控制器、电流采集模块以及作为电路负载的磁流变减振器。首先,基于飞思卡尔单片机设计一款车身姿态控制器。然后,采用Buck电路和PID控制设计了一款带电流反馈的磁流变减振器的驱动器,并通过试验分析驱动器的响应。最后,通过Car Sim RT软件设置不同工况去实时仿真验证控制方法的实用性。

... 在电流驱动器控制方面,目前主要有基于模拟电路原理的负反馈控制^[2,7]以及简单的PID^[3,8]控制或PI^[5]控制 ...

2011

0.0

2007

0.0

. 2007, 1(1):24-31

Auto disturbances rejection control technique

自抗扰控制技术

Han Jing-qing

韩京清

... 针对以上问题,采用韩京清院士^[10]提出的自抗扰控制方法(Active disturbonce rejection controller,ADRC)搭建控制器 ...