作者简介:李因武(1966-),男,副教授,博士.研究方向:工程仿生和地面机器系统分析与模拟.E-mail:lyw@jlu.edu.cn
首先,结合仿生斗齿研究成果,应用Pro/E软件建立了某型反铲液压挖掘机整体三维仿真模型,并导入ADAMS软件中开展运动学和动力学分析。然后,获取了反铲液压挖掘机工作装置的最大挖掘半径、最大挖掘高度、最大挖掘深度、最大卸载高度、最小回转半径等作业范围参数以及斗杆最大挖掘力、铲斗最大挖掘力等主要性能参数。最后,确定动臂参数仿真优化方案为:外侧线与中线夹角为65°、动臂弯曲处的圆弧半径为210 mm。
Combined with the research results of bionic teeth, a three-dimensional virtual model of the working device of a certain type backhoe hydraulic excavator was built in Pro/E software. The kinematics and dynamics of the model were analyzed in ADAMS software. The parameters of the backhoe hydraulic excavator working device were obtained, such as the maximum excavation height, the maximum excavation depth, the maximum unloading height, the minimum turning radius, the maximum excavation force of the stick and the maximum digging force of the bucket. Optimization results of the parameters of the boom of the working device show that the angle between the arc outer line and center line was 65°, and the arc radius of the boom was 210 mm.
动臂是反铲液压挖掘机工作装置的主要部件之一, 直接影响挖掘机的作业性能。国内、外学者就挖掘机的工作装置开展了各方面的研究[1, 2], 张业祥等[3]在斗杆挖掘工况下实测了动臂的应力值, 验证了工作装置有限元模型的有效性。汪建华等[4]建立了有限元模型并开展了自由模态分析和优化, 提高了工作装置结构的刚度, 降低了结构变形并改善了工作装置动态工作性能和结构稳定性。挖掘路径由铲斗挖掘轨迹和动臂挖掘轨迹组成, 通过对铲斗和动臂的位置进行追踪, 有助于准确地分析挖掘机的挖掘性能[5, 6, 7, 8]。在模拟仿真方面, 可基于拉格朗日动力学原理建立挖掘机动力学数学模型, 采用Pro/E和ADAMS软件构建挖掘机工作装置三维模型[9, 10, 11, 12, 13], 应用虚拟样机技术对挖掘机工作装置进行运动学和动力学仿真[14], 获得挖掘机最大挖掘半径、最大挖掘深度、最大挖掘高度、各刚体铰接点处的受力变化情况和受力较复杂的铰接点所受载荷随时间变化的曲线[15, 16]; 采用SolidWorks软件建立机液联合仿真模型, 分析提升工况下液压缸的压力和流量变化情况, 探讨液压系统的适应性和稳定性[17]。
在探讨挖掘机工作装置工作原理的基础上, 诸多学者应用Pro/E、ADAMS、ANSYS等软件对挖掘机工作装置开展运动学和动力学分析, 建立挖掘机工作装置的虚拟样机并开展相关的仿真和优化设计研究, 但针对工作装置动臂的结构参数优化设计方面的研究鲜见报道。本文首先就液压挖掘机工作装置的动臂开展运动学分析, 进而在本实验室仿生研究结果的基础上设计了仿生斗齿, 应用Pro/E软件建立了某型反铲液压挖掘机整体三维仿真模型并导入ADAMS软件中开展运动学和动力学分析, 对基于仿生斗齿的挖掘机工作装置开展仿真优化设计研究。
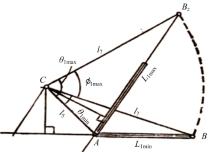
挖掘机动臂的工作过程比较简单[18]。动臂的摆角$\Phi_1$为动臂液压缸长度L1的函数, 动臂上任意一点在任意时刻的坐标值也为L1的函数。图1为挖掘机动臂摆角计算简图。
图1中, L1min、L1max分别为动臂液压缸的最短长度和伸出的最大长度; θ 1min、θ 1max分别为动臂液压缸铰点与动臂下铰点连线所成夹角的最小值和最大值; A点为动臂液压缸的下铰点; B点为动臂液压缸的上铰点; C点为动臂的下铰点; $l_5$为动臂下铰点至动臂液压缸下铰点的长度; $l_7$为动臂下铰点至动臂液压缸上铰点的长度。
如图1所示, 动臂液压缸收缩到最短, 即动臂液压缸长度L1=L1min时, θ 1min在三角形
同理, 动臂液压缸延伸至最长, 动臂液压缸的长度L1=L1max , θ 1max在三角形
动臂的摆角范围为:
动臂的瞬时摆角
通过自然选择及优化, 土壤动物的爪趾结构具有优良的挖掘性能。
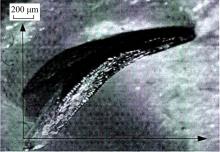
图2所示的蝼蛄属于较典型的土壤生物。蝼蛄的生活环境为土壤, 需要经常挖掘各种洞穴, 其前足(即挖掘足)具有优异的挖掘能力。本文选取蝼蛄为仿生原型, 把其爪趾结构应用到液压挖掘机的斗齿结构设计中, 以期有助于提升工作装置的整体作业效能。
如图3所示, 蝼蛄前足具有类铲状的爪趾形态[19], 其爪趾的外表面(上侧)和内表面(下侧)均为一定弧度的曲面, 爪趾尖端为楔角约为30° 的四方楔状结构。该种结构可降低爪趾掘进过程中的土壤摩擦力, 有助于减轻土壤在爪趾上的粘附。
参照本实验室的仿生研究成果[19], 将蝼蛄爪趾的内、外表面的轮廓点数据导入Matlab软件并进行曲线拟合, 得到蝼蛄爪趾外表面轮廓(上侧)的曲线拟合方程为:
蝼蛄爪趾内表面轮廓(下侧)的曲线拟合方程为:
方程(5)(6)的拟合度分别为0.9877和0.9799。
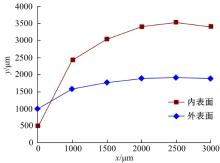
图4为依据方程(5)(6)得到的蝼蛄爪趾的外表面轮廓拟合曲线和内表面轮廓拟合曲线。
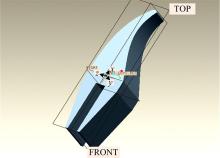
斗齿位于挖掘机铲斗的末端。本文以现代公司生产的R108-9型挖掘机的斗齿为原型, 在Pro/E软件中设计如图5所示的仿生斗齿。用图4中蝼蛄爪趾外、内表面的轮廓拟合曲线代替原型斗齿的上、下侧轮廓线, 同时保证仿生斗齿轮廓线与原型轮廓线相切, 长宽比不变。
以蝼蛄爪趾作为仿生原型设计出的仿生铲斗有助于后续对整个工作装置的仿真优化设计。
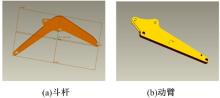
挖掘机工作装置包含15个零件, 主要包括:动臂、斗杆、铲斗、3个液压缸及斗齿等部件。在Pro/E环境中依次通过拉伸、旋转、扫描、混合、孔、倒角、圆角等基础特征和放置特征构建各个零件, 图6为零件图的斗杆和动臂。
装配挖掘机组件时需根据从底向上的原则, 首先完成构件的装配, 然后依次完成整个挖掘机组件的装配。
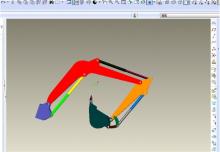
装配挖掘机组件时, 利用“ 插入” 、“ 匹配” 和“ 对齐” 约束依次将基座、旋转平台、驱动臂、平衡缸、铲斗和仿生斗齿导入Pro/E软件中, 用销轴连接相关零件, 而后设置单位、重力加速度、工作栅格等ADAMS工作环境, 添加约束。通过计算可知虚拟样机的自由度为3[18]。为保证挖掘机工作装置自由度为0且没有多余约束, 对动臂液压缸、斗杆液压缸、铲斗液压缸上的移动副各施加1个驱动。图7为装配后的挖掘机工作装置总装图。
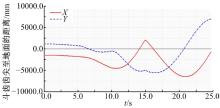
为了便于测量挖掘机工作装置各项数据, 在仿生斗齿齿尖处创建一个测量点(MARKER点)。通过阶跃函数(即step函数)对挖掘机工作装置的运动进行设置, 设定仿真时间为25 s, 步数为500。step函数的设定如下:设定斗杆缸处于全缩位置, 即step(time, 0, 0, 25, -715); 设置铲斗为全缩状态, step(time, 5, 0, 10, 513); 动臂处于工作状态, 其工作过程为先全缩, 后进行全伸, 即运动函数为step(time, 10, 0, 15, 677)+step(time, 15, 0, 25, -893)。函数设定好以后即可通过设置在仿生斗齿齿尖的MARKER点进行仿真。图8为挖掘机工作装置动臂的挖掘运动轨迹图。
利用ADAMS的添加曲线功能, 可将仿生斗齿齿尖MARKER点的
由图9可以看出:在25 s时齿尖与地面垂直距离达到最大, 即最大挖掘高度为6985.04 mm。
类似地, 可以得到如表1所示的挖掘机工作装置作业范围参数的仿真值。
| 表1 工作装置作业范围参数的仿真值 Table 1 Operating range parameters of the work device |
挖掘机铲斗最大挖掘力可定义为通过液压缸作用产生的铲斗切削点最外处的挖掘力, 是挖掘机整机作业性能的主要指标, 也是工作装置优化设计的重要依据。通常将挖掘力分为铲斗液压缸挖掘力、斗杆液压缸挖掘力和动臂液压缸挖掘力。本文研究的目的是对挖掘机工作装置进行优化设计, 因而不考虑动臂液压缸挖掘力。
最大铲斗挖掘力位于由连杆机构和铲斗液压缸产生的最大力矩处, 最大斗杆挖掘力位于斗杆液压缸和铲斗共同作用产生的最大力矩处。为了对挖掘机铲斗最大挖掘力进行仿真, 需修改挖掘机工作装置的三维模型姿态, 调节铲斗液压缸活塞杆, 使铲斗与斗杆的铰接点到斗杆液压缸推力作用线最远。
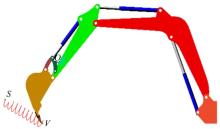
在铲斗最大挖掘力仿真模型中(见图10), 铲斗与斗杆的铰接点、齿尖分别被命名为
为获取挖掘机铲斗最大挖掘力的仿真值, 需在ADAMS界面中确定固定点(S点)并且满足QV $\perp$ SV。通过向量计算得S点坐标为(-5800, -200, 0), 在S点处建立标识点, 建立条件选为Add to ground, 而后在
弹簧与铲斗之间会形成相互作用力, 应用弹簧起到模拟测力计的作用。本文研究中挖掘机铲斗油缸内径d为0.08 m, 液压系统工作压力为20 MPa, 根据压力公式
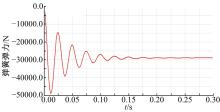
分别设定斗杆驱动和动臂驱动为0* time, 删除铲斗驱动, 则挖掘机工作装置只有一个自由度, 即动臂和斗杆处于无运动状态。动力学仿真时, 设置仿真时间为0.3 s, 步数为150, 然后选择弹簧, 进入Adams/PostProcessor, 得到与铲斗对应的弹簧弹力变化曲线, 如图11所示。
铲斗最大挖掘力的仿真值为弹簧弹力的相反数。通过图11可知, 弹簧弹力在经过0.2 s的震荡后达到平衡, 平衡值为-28 834.5 N, 弹簧弹力的相反数即铲斗最大挖掘力为28 834.5 N。类似可求出斗杆最大挖掘力的仿真值为17 944.1 N。
本文针对动臂弯曲处的圆弧半径
挖掘机的动臂结构参数中, 动臂弯曲处的圆弧半径
(1)增大弯曲处圆弧半径, 由200 mm变为210 mm。
(2)减小弯曲处圆弧半径, 由200 mm变为190 mm。
(3)增大动臂外侧线与中线的夹角, 由67° 变为70° 。
(4)减小动臂外侧线与中线的夹角, 由67° 变为65° 。
(5)同时增大动臂的外侧线与中线夹角和弯曲处圆弧半径, 即夹角为70° , 圆弧半径为210 mm。
(6)将动臂的外侧线与中线夹角变小, 而弯曲处圆弧半径增大, 即夹角变为65° , 圆弧半径为210 mm。
(7)增大动臂最外侧线与中线的夹角, 减小弯曲处圆弧半径, 即夹角变为70° , 弯曲处圆弧半径变为190 mm。
(8)减小动臂最外侧线与中线的夹角, 减小弯曲处圆弧半径, 即夹角变为65° , 弯曲处圆弧半径变为190 mm。
将上述8种调整方案应用于挖掘机工作装置仿真模型中, 获取8组部分作业范围参数和主要性能参数的仿真值, 与夹角、圆弧半径不变的原型机的相关参数的仿真值做汇总处理, 9组仿真结果如表2所示。
| 表2 各组仿真值汇总 Table 2 Summary of simulation values |
由表2可知, 最大挖掘半径的最大值为7074.54 mm, 最大挖掘高度的最大值为7316.51 mm, 出现在第4组, 此时动臂外侧线与中线的夹角为65° , 其他参数未变; 最小回转半径的最大值出现在第8组数据中, 即动臂弯曲处圆弧半径为190 mm、外侧线与中线夹角为65° 处; 最大挖掘深度的最大值为7476.34 mm, 最大斗杆挖掘力的大小为18 346.9 N, 最大铲斗挖掘力的大小为32 075.2 N, 都位于第6组, 此时动臂尺寸参数为弯曲处圆弧半径210 mm、动臂外侧线与中线的夹角65° ; 最大卸载高度的最大值6396.28 mm, 此时动臂的各项尺寸均未发生变化。对于挖掘机的工作装置, 其作业范围和最大挖掘力的增加, 将扩大挖掘机的适用范围, 提高挖掘机的整体工作效率。
由表2可知, 最大挖掘半径和最大挖掘高度在第4组获得, 最大挖掘深度在第6组获得, 而最大挖掘力出现在第6组, 即参数尺寸为弯曲处圆弧半径210 mm以及外侧线与中线的夹角65° 的设计状态。对比分析第4组和第6组的数据可发现, 两组数据中动臂作业范围参数的数值相差不大。因此, 从提升挖掘机作业性能的角度出发, 选择第6组调整方案, 即弯曲处圆弧半径为210 mm以及动臂外侧线与中线的夹角为65° 作为动臂尺寸参数的仿真优化方案。
本文以典型反铲液压挖掘机的工作装置为原型, 在实验室相关仿生研究成果上设计了仿生斗齿。应用Pro/E软件对反铲液压挖掘机整体进行了三维仿真建模, 在ADAMS软件中对创建的虚拟模型进行了运动学和动力学分析, 获取了反铲液压挖掘机工作装置的最大挖掘半径、最大挖掘高度、最大挖掘深度、最大卸载高度、最小回转半径等作业范围参数, 以及斗杆最大挖掘力、铲斗最大挖掘力等主要性能参数。通过调整工作装置动臂的尺寸参数, 在ADAMS中进行仿真试验并得到作业范围参数和主要性能参数的8组仿真试验数据, 将其与动臂尺寸未变的工作装置的测量数据进行汇总对比, 最终确定外侧线与中线夹角65° 、动臂弯曲处的圆弧半径210 mm为动臂参数仿真优化方案。研究结果和思路为反铲液压挖掘机及类似工程机械的结构优化设计提供了基础数据和技术手段。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|