全局相机姿态优化下的快速表面重建

引用本文

林金花, 王延杰, 王璐, 姚禹. 全局相机姿态优化下的快速表面重建[J].吉林大学学报（工学版）, 2018,48(3): 909-918
LIN Jin-hua, WANG Yan-jie, WANG Lu, YAO Yu. Real-time surface reconstruction based global camera pose optimization[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 909-918 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170146
Permissions

全局相机姿态优化下的快速表面重建

林金花¹, 王延杰², 王璐¹, 姚禹³

1.长春工业大学应用技术学院,长春 130012

2.中国科学院长春光学精密机械与物理研究所,长春 130033

3.吉林大学机械科学与工程学院,长春 130012

作者简介:林金花(1980-),女,讲师,博士.研究方向:数字图像处理、目标识别与跟踪.E-mail:ljh3832@163.com

基金:“863”国家高技术研究发展计划项目(2014AA7031010B); 吉林省教育厅“十三五”科学技术研究项目(吉教科合字[2016]345).

摘要

针对传统三维重建算法存在的漂移问题,提出了一种端到端的在线大规模三维场景重建算法。首先,使用一种在线估计策略来鲁棒地确定相机的旋转姿态,同时构建层次优化框架用于融合深度数据的输入。然后,依据相机的全局估计姿态对每一帧的信息进行优化,解除了算法对目标跟踪时间的限制,完成了对帧间关系对象的实时跟踪。试验结果表明:本文算法的平均重建时间为399 ms,平均估计迭代最低点(ICP)次数为20,完成每帧变换的时间为100 ms;系统对大规模场景的重建具有鲁棒性,且实时性较好,是一种具有对应关系稀疏特性、结构信息稠密特性和相机光照一致特性的实时三维重建算法。

关键词: 计算机应用; 机器视觉; 三维重建; 实时体素融合; 姿态估计

中图分类号:TP391;TH691 文献标志码:A 文章编号:1671-5497(2018)03-0909-10

Real-time surface reconstruction based global camera pose optimization

LIN Jin-hua¹, WANG Yan-jie², WANG Lu¹, YAO Yu³

1.School of Application Technology, Changchun University of Technology, Changchun 130012,China

2. Chinese Academy of Sciences, Changchun Institute of Optics, Fine Mechanics and Physics,Changchun 130033, China

3.College of Mechanical Science and Engineering, Jilin University, Changchun 130012,China

Abstract

An end-to-end online large-scale 3D scene reconstruction method is proposed. This method uses robustness to estimate the rotation attitude of the camera and constructs a hierarchical optimization framework for the fusion of depth data input. Then, the information of each frame is optimized according to the global pose of the camera, and the algorithm limits the target tracking time and completes real-time tracking of the frame. Experimental results show that the average time to reconstruct the algorithm reaches 399 ms and the average number of estimated Iterative Closest Point (ICP) times is 20, which needs 100 ms to complete each frame transformation. The system is robust to the reconstruction of large-scale scenes and has better real-time performance. This method is a real-time three-dimensional reconstruction system with corresponding sparseness, dense structure information and camera illustration uniformity.

Keyword: computer application; machine vision; 3D reconstruction; online volume fusion; pose estimation

文章图片

0 引言

近年来, 获取二维图像并重建三维场景技术的应用范围不断扩大, 主要包括机器视觉系统、三维制造行业以及图像增强等方面。作为用户或机器人需要实时扫描整个房间或多个空间, 将累积的3D模型瞬间、连续地融合到目标应用中; 机器人导航需要将物理世界映射到虚拟世界, 在扫描期间提供即时的信息反馈。这些需求使得研究人员开始对大规模场景的实时重建展开研究。

在过去的几十年, 研究人员对三维重建方法展开了大量的研究。三维重建方法使用多传感器获取底层数据信息, 包括使用点数据信息融合的表示方式^{[1, 2, 3, 4]}、2.5维度的RGB-D数据表示^{[5, 6]}、基于高度信息融合的数据表示^[7]以及应用广泛的三维体素融合方法^{[8, 9]}。基于隐式截断距离场(Truncated signed distance felds, TSDF)的三维重建算法是一种鲁棒性强的三维体素融合方法^[10], 该方法使用连续函数编码几何表面信息, 对噪声具有抗干扰特性, 且不再受表面拓扑结构的制约。

体素融合算法需要表面几何均匀分布, 不具有普遍适用性, 为了改善这个问题, 科研工作者提出了各种改进算法来实现空间体素融合^{[11, 12]}, 使用截断式带符号距离函数表示空间几何结构表面信息是一种普遍适用的表示形式。该算法虽然支持大规模场景的体素融合过程, 然而姿态漂移问题仍然存在, 导致重建后的三维场景失真现象严重。

使用深度图接收的三维重建算法一般要求是非在线算法, Zhou等^[13]给出的使用全局相机位置优化的三维重建算法, 通常需要花费1 h以上的时间完成重建。同步定位映射(Simultaneous localization and mapping, SLAM)算法的关键在于准确估计相机位置, 研究者给出了具有在线重建特性的单向深度重建算法, 主要包含具有稀疏特性的重建算法、具有半稠密特性的重建算法以及直接三维重建算法^{[14, 15]}。以上各种算法使用单目深度传感器获取目标场景的姿态图并完成场景的捆绑调整过程, 实现了误差最小化, 然而无法构建精度高的三维表面。

单项体素重建融合算法实现了SLAM算法的稀疏绑定过程, 完成了稠密三维体素的融合过程, 三维重建结果较好, 然而对于大规模的场景重建效果一般。SLAM算法重建一般使用帧到帧的融合算法实现相机位置估计, 同时使用离线算法调整相机位置, 引起重建速率大幅度下降。Newcombe等^[16]给出了从图像帧到三维表面的实时检测架构, 实现了从稀疏到稠密的密集三维场景重建, 无需调整重建模型, 然而该算法不适应于大规模场景的三维重建。

迭代最近点(Iterative closest point, ICP)相机位置估计方法使用最近点距离函数预测对象目标位置, 然而重建精度受到影响。研究者使用深度图和整体相机位置估计方法来提高重建算法的精度^[17], 包括采用优化目标姿态、检测对象的闭环、绑定位置优化以及基于坐标点与二维图像的重新定位策略来优化目标跟踪过程。这些方法可以实现对三维目标场景的实时重建, 然而优化过程通常需要较长时间, 且闭环策略需要相对繁杂的定位轨迹, 因此对相机运动轨迹是有制约的; 另外, 根据在体素融合前的跟踪信息生成相机运动轨迹, 相对制约了三维场景的优化精度。

针对上述问题, 本文给出了一种CPU端到GPU端的在线体积重建算法, 其关键思想是基于一种相机姿态的鲁棒估计策略, 全局优化每一帧的相机运动轨迹, 同时将深度数据信息融合到一个具有层次架构的整体优化框架中。算法对每个深度帧进行整体到局部的对应关联, 对闭环包的处理主要使用隐含方法进行, 解决了复杂的闭环检测过程。当系统发生检测失败现象时, 跟踪被终止时, 可以从另外一个视角重新启用跟踪, 因此重建鲁棒性较好。

1 系统概述

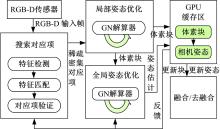
本文使用一种全局相机姿态优化策略, 实现对每一帧图像信息的实时位置优化, 根据优化后的相机姿态来更新下一帧信息, 算法兼容摄像机运动轨迹的多角度变化, 快速定位目标位置且快速重新访问目标区域, 可有效处理遮挡问题, 完成帧间数据的在线跟踪定位, 为大规模场景的在线重建提供了理论基础, 系统重建流程如图1所示。

	Figure Option View Download New Window
	图1 系统重建流程框图Fig.1 Block diagram of reconstruction system

(1)根据RGB-D传感器取得深度数据信息, 同时基于稀疏对应关系组合得到整体到局部的对应关系, 接着使用最优密集光照和拓扑对应关系来优化对应关系, 得到尺度不变特征变换(Scale invariant feature transform, SIFT), 查询全部帧间信息对应的SIFT值, 同时使用滤波器过滤异常信息。

(2)在相机全局运动轨迹对准过程中, 使用帧间层次优化策略对全局相机姿态进行优化处理。在第1层优化过程中, 由 $n$ 个连续帧组成“ 块” 单元, 针对“ 块” 完成局部优化过程; 在第2层优化过程中, 实现“ 块” 与“ 块” 的对应关联进而实现全局整体优化。本文算法使用截断式带符号距离场生成对应“ 块” 。同时依据滤波策略的对应关系和稠密的光照拓扑限制完成该级的相机姿态对应关系优化, 本文使用层次优化策略降低优化层间的非关联对应关系的特征关联, 该算法可用于大规模场景的三维重建过程; 使用GPU的内部非线性迭代解算器完成层级间的非线性问题计算。

(3)根据全局相机姿态优化下的三维场景帧对下一帧信息进行更新, 实现深度数据帧的快速融合, 同时用基于反向融合策略得到帧信息代替在过去相机姿态下获取的深度帧信息, 同时更新当前帧信息。重复此步骤直到重建精度达到阈值要求, 该策略保证了算法对大规模场景的重建精度。

2 全局姿态对准策略

使用全局相机姿态对准策略的实时三维重建的核心是鲁棒性强的整体分层姿态优化过程。输入数据是由深度传感器获取的深度流: $S = {f_{i} = (C_{i}, D_{i} {)}}_{i},$ 其中, $C_{i}$ 为每一帧的颜色信息, $D_{i}$ 为RGB-D信息。深度传感器的运动捕获速率为30 Hz, 分辨率为640× 480。全局对应关系检测是在帧数据间获取三维对应关系项, 同时根据相机位置变换的集合信息 ${Γ_{i}},$ 实现全部帧的运动对准。对第 $i$ 帧数据进行坐标系变换操作, 使其从局部坐标系映射到三维坐标系:

$Γ_{i} (p) = R_{i} p + t_{i}$

式中: $p$ 为三维空间点坐标; $R_{i}$ 为相机旋转角度; $t_{i}$ 为相机平移位置距离, 此处建立初始帧的位移全局坐标系。

2.1 特征对应匹配

本文基于目标特征匹配和相应的滤波策略来检测帧间的稀疏对应关系组合。准确的对应关系组合对应精准的全局优化过程至关重要, 下面将主要阐明对应关系的检测滤波过程。

对于每个新获取的帧数据, 计算SIFT特征值, 同时将该帧信息对应到全部先前帧处。SIFT用于说明深度信息的检测结果变化情况, 例如缩放, 平移, 旋转等步骤。然后对帧间数据进行滤波操作, 生成对应关系组合, 该组合用于全局相机姿态优化过程, 该过程如图2所示。该步骤主要在GPU上完成, 减少了数据备份视觉, 降低了中央处理器开销。本文计算SIFT信息描述符的速率大概是4~5 ms/帧, 帧间对应关系匹配时间是0.05 ms。对于新获得的深度帧信息, 该算法可同时在线检测2× 10⁴帧。

	Figure Option View Download New Window
	图2 本文算法的匹配过程Fig.2 Matching process of proposed algorithm

对应异常值的处理过程, 本文使用光照和拓扑对应特性来滤掉已有的对应关系组合。

首先, 对于帧对组合 $f_{i}$ 和 $f_{j},$ 二者对应检索到的三维坐标点为 $P 和 Q,$ 该帧与点间的对应策略记为对应关系选项。使用滤波策略找到对应关系选项, 对应关系选项符合稳态分布, 同时具有较为一致的刚性转换特性, 对应关系选项依据测试距离与对应关系吻合。刚性变换计算公式如下: $Γ_{ij} (p) = (Γ_{j}^{- 1} Γ_{i}) (p),$ 检测对应项 $P_{cur}$ 和 $Q_{cur},$ 计算分布和协方差值, 避免刚性变换的不匹配特性, 例如, 当对应关系选项出现在曲线之上, 且具有旋转对称特征, 说明系统具有不稳定性。

其次, 计算帧 $f_{i}$ 所关联的对应关系点 $P,$ 同时计算 $f_{j}$ 与对应关系点 $Q$ 间的面积差集, 在每个三维点的计算过程中, 将这些点映射到对应的主轴平面, 同时依据映射坐标点的包围框计算其表面面积。当该面积值小于0.032 m²时, 则将对应关系选项从对应组合中去除。

最后, 本文对拓扑结构和光照检测进行密集处理, 基于关键坐标点与滤波检测相互匹配的测量, 获取对应关系变换 $Γ_{ij},$ 实现 $f_{i}$ 与 $f_{j}$ 的对应匹配过程, 检测在不同相机运动轨迹上的重复映射深度偏差值、法线偏移量和光照匹配度。在改善三维重建效率方面, 定义接收区域尺寸为长× 宽=24× 18 m², 同时, 在池化层上处理帧间匹配, 同时当取得新深度数据帧 $f_{i}$ 时, 其池化RGB强度值为 $C_{i}^{low},$ RGB-D值为 $D_{i}^{low},$ 相机三维运动轨迹坐标为 $P_{i}^{low},$ 法线坐标值为 $N_{i}^{low},$ 全部由GPU存储并处理。从帧 $f_{i}$ 到帧 $f_{j}$ 的映射误差值为:

$E_{r} (f_{i}, f_{j}) = \sum_{x, y} ‖ Γ_{ij} (p_{i, x, y}) - q_{j, x, y} ‖_{2} (1)$

式中:

$p_{i, x, y} = P_{i}^{low} (x, y), q_{j, x, y} = P_{j}^{low} (π^{- 1} (Γ_{i, j} p_{i, x, y})) 。$

2.2 姿态对准(能量优化)

(1)给定一组帧数据(块或关键帧内的帧, 取决于层次水平)之间的三维对应项, 姿态对准的目标是找到每个帧 $f_{i}$ (简称 $i$ )的刚性相机变换 ${Γ_{i}}$ 的最优集合。由斜对称矩阵发生器来实现对4× 4刚性变换 $Γ_{i}$ 的参数化处理, 留下3个未知参数用于旋转操作, 另外3个用于平移操作。为了便于表示, 本文将所有帧 $S$ 的自由度叠加到一个参数向量中:

$χ = (R_{0}, t_{0}, \dots, R_{|S|}, t_{|S|})^{T} = (x_{0}, x_{1}, \dots, x_{N})^{T} (2)$

式中: $N$ 为向量 $x_{i}$ 的总数。

本文将对齐问题定义为未知参数 $χ$ 的非线性最小二乘化问题, 并基于稀疏特征、密集光度和几何约束来定义对准目标, 如下所示:

$\begin{array}{l} E_{align} (χ) = ω_{sparse} E_{sparse} (χ) + ω_{sparse} E_{dense} (χ) \\ (3) \end{array}$

式中: $ω_{sparse}$ 和 $ω_{dense}$ 分别为稀疏和稠密匹配项的权值, $ω_{dense}$ 的迭代增加用于表示粗略的姿态对准。

注意, 参考帧表示块中的第1帧, 用于块内对齐; 或表示整个输入序列中的第1帧, 用于全局块内对齐。因此, 参考变换 $Γ_{i}$ 不是自由变量, 并可从优化中省略。

在稀疏匹配项中, 本文对所有帧间的特征对应项的世界空间位置距离之和进行最小化处理:

$E_{sparse} (χ) = \overset{|S|}{\sum_{i = 1}} \overset{|S|}{\sum_{j = 1}} \sum_{(k, l) \in C_{i, j}} ‖ Γ_{i} p_{i, k} - Γ_{j} p_{j, l} ‖^{2} (4)$

式中: $p_{i, k}$ 为第 $i$ 帧的第 $k$ 个检测到的特征点; $C_{i, j}$ 为第 $i$ 帧和第 $j$ 之间的所有成对的对应关系(对应项)的集合。

式(4)的含义是寻找最优的刚性变换 $Γ_{i},$ 使得所有被检测到的特征匹配的欧几里德距离最小。

(2)本文使用密集光度和几何约束进行精细尺度对准, 计算每个输入帧的颜色 $C_{i}$ 和深度 $D_{i}$ 的密集像素信息。密集对齐的计算量比稀疏对齐要大得多。因此, 本文在每个帧对应项的有限集合 $E$ 上进行计算。 $E$ 为对稀疏匹配图边缘 $(i, j)$ 的编码, 如果帧 $i$ 与帧 $j$ 对准(即它们的相机角度相似, 在60° 内)且彼此重叠, 则密集光度和几何对准的优化采用如下的能量公式表示:

$E_{dense} (Γ) = ω_{photo} E_{photo} (Γ) + ω_{geo} E_{geo} (Γ) (5)$

式中: $ω_{photo} 、 ω_{geo}$ 分别为几何项和光度项的权值。

对于密集光度一致性, 通过计算亮度 $C_{i}$ 在梯度 $Γ_{i}$ 上的误差获得鲁棒的亮度变化:

$\begin{array}{l} E_{photo} (χ) = \\ \sum_{(i, j) \in Ε} \overset{|Γ_{i}|}{\sum_{k = 0}} ‖ Γ_{i} [π (d_{i, k})] - Γ_{j} [π (Γ_{j}^{- 1} Γ_{i} d_{i, k})] ‖_{2}^{2} (6) \end{array}$

式中: $π$ 表示透视投影; $d_{i, k}$ 为与第 $i$ 个深度帧的第 $k$ 个像素相关联的3D坐标。

通过计算点到平面的几何度量获取切平面的精细度量对准:

$\begin{array}{l} E_{geo} (χ) = \sum_{(i, j) \in Ε} \overset{|D_{i}|}{\sum_{k = 0}} [{n^{T}}_{i, k} (d_{i, k} - \\ Γ_{i}^{- 1} Γ_{j} π^{- 1} (D_{j} (π (Γ_{j}^{- 1} Γ_{i} d_{i, k} {))))]}^{2} (7) \end{array}$

式中: $n_{i, k}$ 为第 $i$ 个输入帧的第 $k$ 个像素的法线。

这里忽略输入帧之外投影的对应项, 并且在每个优化步骤之后, 使用ICP约束项来测量帧间距离和法线约束。对于密集的光度和几何约束, 本文将 $Γ_{i}$ 和 $D_{i}$ 减小到80像素× 60像素(使用与密集验证过滤器相同的高速缓存帧)。对于全局姿态优化, 通过稀疏对应优化来有效地重置每个关键帧处的密集优化结果, 本文仅在扫描结束之后执行密集全局关键帧的优化, 优化后的匹配效果如图3所示。

	Figure Option View Download New Window
	图3 本文重建算法的层次匹配效果Fig.3 Matching results of proposed reconstruction algorithm

2.3 鲁棒的快速优化策略

全局姿态对准是未知相机参数的非线性最小二乘问题。为了实现对超过两万帧的长扫描序列进行在线全局相机姿态优化, 本文采用一种基于GPU的非线性迭代求解器, 由于稀疏模式需要不同的并行化策略, 本文采用高斯-牛顿方法(一阶可导, 二次收敛), 通过计算非线性最小二乘方来寻找最优姿态参数 $χ^{2},$ 即:

$χ^{2} = \underset{χ}{argmin E_{align} (χ)} (8)$

为了便于表示, 本文以规范最小二乘法形式表示:

$E_{align} (χ) = \overset{R}{\sum_{i = 1}} r_{i} {(χ)}^{2} (9)$

式中: $R = 3 N_{corr} + |Ε| \cdot (|Γ_{i}| + |D_{i}|), N_{corr}$ 为用于块间对齐的稀疏对应项的数量或用于块内对齐的每块稀疏对应项。

通过定义向量域 $F : R^{N} \to R^{R}$ 来简化符号:

$F (χ) = {[\dots, r_{i} (χ), \dots]}^{T} (10)$

这里使用 $F (χ)$ 的欧几里德长度的平方表示为: $E_{refine} (χ) = ‖ F (χ) ‖_{2}^{2} 。$ 通过使用一阶泰勒展开式求解 $χ^{k - 1},$ 进而生成 $F (χ)$ 的局部线性近似公式:

$\{\begin{array}{l} F (χ^{k}) = F (χ^{k - 1}) + J_{F} (χ^{k - 1}) Δ χ \\ Δ χ = χ^{k} - χ^{k - 1} \end{array} (11)$

式中: $J_{F}$ 为 $F (χ)$ 的雅可比特征值。

用式(11)所示的局部近似代替 $F (χ),$ 通过求解线性最小二乘问题来找到最佳参数更新 $Δ χ^{*},$ 即:

$Δ χ^{*} = \underset{Δ χ}{argmin} \underset{E_{lin} (Δ χ)}{\underset{︷}{‖ F (χ^{k - 1}) + J_{F} (χ^{k - 1}) \cdot Δ χ ‖_{2}^{^{2}}}} (12)$

为了获得最小值 $Δ χ^{*},$ 设对于 $\forall i,$ 偏导数 $\frac{d E_{lin}}{dΔ χ_{i}} (Δ χ_{i}^{*}) = 0,$ 得到如下的线性方程:

$J_{F} (χ^{k - 1})^{T} J_{F} (χ^{k - 1}) Δ χ^{*} = - J_{F} (χ^{k - 1})^{T} F (χ^{k - 1}) (13)$

系统在GPU上并行处理共轭梯度(PCG)求解器, 并使用雅克比预处理器来求解式(13), 同时使用迭代策略求解系统矩阵 $J_{F} (χ^{k - 1})^{T} J_{F} (χ^{k - 1})$ 的稀疏度。利用高斯-牛顿迭代法求解局部线性化能量以及相关的线性最小二乘问题, 并基于最后一帧的计算结果执行优化处理。

系统使用单一内核计算最佳步长, 更新相机下降方向和全局-局部切换来累积得到最终扫描结果, 使用PCG算法构建系统矩阵以及当前下降方向。首先考虑稀疏特征项, 为了避免填入, 基于两个单独的内核调用递增地乘以系统矩阵:第1个内核乘以 $J_{F};$ 在第2个内核调用中乘以 ${J^{T}}_{F} 。$ 由于 $J_{F}$ 和 ${J^{T}}_{F}$ 有不同的逐行稀疏模式, 使用两个不同的内核调用有助于将并行化方法调整到全局应用。具体地说, 对于稀疏项, 每行 $J_{F}$ 根据至多2个外部相机姿势或2× 6=12个非零矩阵条目精确地编码成对应项。由于所需操作的数量较少, 可以通过向每个3D块行分配一个专用线程来计算矩阵向量积, 即处理对应关系的 $x -, y -$ 和 $z -$ 残差。因为不同的维度在评估 $F 和 J_{F}$ 时使用相同的操作, $J^{T}$ 对于每个未知项都有一行操作, 每行中的非零项的数量等于未知帧的对应项数量。对于较长的扫描序列, 这将导致每行数千个条目, 为了减少每个线程的内存读取和计算量, 本文选择了简化的方法来计算矩阵向量积。使用一个大小 $N_{block} 为 256$ 的块来计算每个行方向的点积, 块的每个线程基于内部本征来执行线程, 每个线程结果基于共享存储器单元组合而成。为了计算 ${J^{T}}_{F},$ 预先计算辅助列表, 允许查找某个变量的所有对应关系, 该表对每个通信的单个线程内核进行填充, 并且将条目添加到相关联变量的对应项列表中。使用原子计数器管理每个列表的存储器, 当对应项的集合改变时, 则重新计算该表。

对于精密的光度和几何对准项, 相关残留的数量相当高。由于系统矩阵在PCG工作期间固定, 本文在每个非线性迭代开始时预先计算它。所需的内存是预分配的, 本文只通过分散写入更新非零项即可。注意, 随着共享内存局部特性的减少, 只需要少量的写入操作。

作为一种优化措施, 本文系统在每次优化结束之后执行对应项帧过滤, 该操作对于潜在的通信异常值(被错误地认为是有效的)的处理是鲁棒的。也就是说, 使用GPU的并行缩小操作来确定最大残差 $r_{\max} = ma x_{i} r_{i} (χ),$ 当 $r_{\max}$ > 0.05 m时, 去除与 $r_{\max}$ 关联的两个帧 $i$ 和 $j$ 之间的所有对应项。注意, 去除 $i$ 和 $j$ 之间的所有对应, 以便最小化优化次数以及所有不佳对应关系的次数。另外, 对于没有对应关系的帧, 则其被隐含地从优化中移除并且被标记为无效。

3 动态3D重建

本文使用全局摄像机的对准姿态优化策略完成大规模场景的鲁棒重建。检测帧间的对应关系变化过程, 使用体素融合与体素去融合的方式完成目标场景的三维体素变更。因此, 当算法搜索到较优的估计姿态时, 便可实现目标场景的精准重建, 减少了累积误差, 同时降低了漂移率。

3.1 三维场景表示

基于体素数据结构表示的三维重建策略, 使用带符号距离场(TSDF)来表示目标对象的几何信息, 并将全部深度信息融合到该表示结构中, 实现对场景信息的完整表征。TSDF表示方式基于体素空间的拓扑结构表示, 用于存放TSDF信息的数据结构较复杂, 同时会影响算法的效率, 因此, 本文使用Lin等^[18]提出的方法来完成重建, 空余三维空间无需表示, 算法基于三维体素索引策略, 使用稀疏体素网格存放每个TSDF值, 这里定义体素大小为8 cm× 8 cm× 8 cm。另外, 在实时更新相机姿态的过程中, 本文使用融合和去融合方法将深度信息整合到了TSDF空间表示中^{[19, 20]}。

3.2 体素的融合及去融合

对于复杂场景中的每个空间体素, $D (v)$ 为体素的带符号距离; $W (v)$ 为三维体素的权重, $d_{i} (v)$ 为映射距离值, $w_{i} (v)$ 为每个 $D_{i}$ 的融合权重。具体的体素融合函数表示, 如下所示:

$\{\begin{array}{l} D' (v) = \frac{D (v) W (v) + w_{i} (v) d_{i} (v)}{W (v) + w_{i} (v)} \\ W' (v) = W (v) + w_{i} (v) \end{array} (14)$

体素的去融合更新操作如下所示:

$\{\begin{array}{l} D' (v) = \frac{D (v) W (v) - w_{i} (v) d_{i} (v)}{W (v) - w_{i} (v)} \\ W' (v) = W (v) - w_{i} (v) \end{array} (15)$

本文算法针对当前帧执行融合操作, 将上一帧的信息融合到当前帧, 同时对上一帧执行去融合操作, 去掉冗余值, 融合后的场景信息较好地保留了原始的几何拓扑结构信息, 同时为下一帧的融合过程提供依据, 这种策略在保证重建精度的同时, 避免了不必要的整合, 提高了算法的重建效率。

3.3 重建更新

本文采用GPU缓存来存放重建帧的RGB-D数据。算法快速地将当前帧信息融合到重建过程中的各个TSDF中, 保证了视觉系统的实时更新性能。算法使用相机全局优化策略来更新整体体素信息, 使用滤波器对关键对应关系点进行优化, 减少了漂移现象, 保证了算法的鲁棒性^{[21, 22, 23, 24]}。

本文算法在重建更新的过程中, 对帧进行降序排序, 进而实现重建过程的择优融合。重建融合的DOF参数设置如下: $α 、 β 、 γ$ 表示相机姿态变换角度; $x 、 y 、 z$ 表示相机移动位置; $t_{int} = (α_{i}, β_{i}, γ_{i}, x_{i}, y_{i}, z_{i})$ 表示融合; $t_{opt} = (α_{0}, β_{0}, γ_{0}, x_{0}, y_{0}, z_{0})$ 表示重建更新; 二者间的带符号距离为 $‖ s t_{int} - s t_{opt} ‖_{2}, s = (2, 2, 2, 1, 1, 1),$ 针对每个帧数据完成以上融合和更新重建。

4 试验结果及分析

4.1 试验环境参数

为了测试本文系统的性能, 选取不同照明条件来完成大规模真实场景的三维重建过程。软硬件配置如下:操作系统为Windows 10; 编程环境为VS 2016; 中央处理器型号为INTEL Core i5; 图形处理器型号为NVIDIA 1070i/8G; 深度传感器为Asus Xtion Pro; 传感器的帧绘制速率为30 Hz/s, 捕获信息分辨率为640× 480。

重建的视觉反馈被流传输到系统界面以帮助扫描过程。本文采用数据压缩方式处理帧数据流, 以此减少带宽的限制。采用CUDA 8.0框架完成相机姿态的全局对应。本文选取了6个不同的三维场景实施重建, 其中包括4个房间M₁~M₄, 一个桌面M₅, 一个纹理墙M₆以及长80 m的帧序列, 重建结果显示相机姿态的对准率较好, 无显著的摄像机漂移现象。

4.2 定量分析

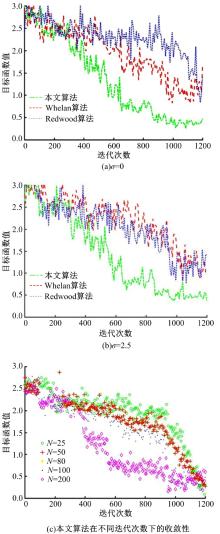
采用定量评估的方式测试本文算法的重建性能, 当预设重建点云数量和噪声干扰强度的前提下, 构建500种测试用例, 针对采样噪声组, 分成5组用例和5级噪声。本文给出了包括Whelan、Redwood以及本文算法的性能对比图, 如图4所示。在噪声强度的影响下, 三维重建点的位置也变化, 同时目标函数随迭代次数的增加而变化。根据试验结果显示, 算法的收敛性与重建三维点符合线性变换关系, 然而当噪声强度不同的情况下, 算法的收敛性也会受到影响。本文算法适用于大规模点云数据的实时三维重建, 且重建精度较高。

	Figure Option View Download New Window
	图4 Whelan、Redwood及本文算法的收敛性Fig.4 Comparison of Whelan、Redwood and our algorithm for convergence

这里对图5所示的三维场进行重建, 以此来测试算法的重建精度。当输入数据不包含噪声干扰时, 即使外点数量增加, 也不会影响三维场景的重建精度; 另外, 当输入数据包含噪声干扰时, 场景的重建精度也无明显变化, 表明本文算法具有抗干扰特性, 尤其对噪声干扰及外点数量具有鲁棒性。

	Figure Option View Download New Window
	图5 纹理墙模型M ₆三维重建效果图Fig.5 Texture wall model M₆ three dimensional reconstruction result

4.3 定性分析

本组试验使用NVIDIA GeForce GTX Titan X和GTX Titan Black组合技术。Titan X用于体积重建, Titan Black用于对应搜索和全局姿态优化。对于所有的测试场景, 本文算法采用大于30 Hz的速率来获取目标场景, 在整体稠密更新的后续帧中, 绘制速率小于500 ms/帧, 三维重建结果如图6所示。从图6可以看出:本文算法与Whelan、Redwood算法相比, 重建质量相当甚至针对大规模缺损场景的重建, 本文算法表现得更好, 重建精度与离线重建算法的重建精度相当, 这是一般在线算法很难达到的精度, 重建效果显示无漂移, 对于结构纹理复杂的曲面, 重建效果较好、无伪影。

	Figure Option View Download New Window
	图6 系统大规模重建效果图Fig.6 System large scale reconstruction map

本文算法与Whelan、Redwood算法的比较结果显示:Whelan、Redwood算法在使用深度传感器获取场景并重建的过程中, 漂移现象严重, 尤其对规模较大的三维场景, 累积误差明显。本文算法使用全局相机姿态优化策略, 在保证重建精度的情况下, 满足了大规模场景的实时重建需求, 同时漂移现象较小, 如图7所示。

	Figure Option View Download New Window
	图7 本文系统重建恢复(M₅)Fig.7 Reconstruction recovery of our system(M₅)

为测试本文算法对遮挡情况的鲁棒性, 选取实物对目标场景进行遮挡测试。当目标场景被遮挡后, 本文算法可实现快速的恢复更新重建, 恢复速率较高, 以至于重建漂移不明显, 仅存在于小面积范围内, 当遮挡物被快速移除时, 本文算法具有不敏感特性, 几乎对场景重建精度无任何影响。由此可见, 本文算法的重建过程对遮挡现象具有鲁棒性, 且同时具有中断后快速更新复原特性, 适用于大规模复杂场景无遮挡、无伪影的快速重建。

本文算法能够鲁棒地处理循环闭包, 如图8所示。体素三维重建以持续的融合过程对相机获取的帧数据流进行更新处理, 同时完成几何结构的实时融合和去融合处理, 同时对循环闭包进行鲁棒重建处理。当摄像机的定位发生变动时, Whelan算法对小区域场景的重建精度较差, 漂移现象较严重; Redwood算法在三维重建精度方面比Whelan算法要好, 然而随着重建场景规模的扩大, 两种算法的重建速率下降, 因此不适应于大规模场景的实时重建。本文算法在初始帧获取阶段, 显示出些微错误检测现象, 然而随着传感器采用数据的增加, 相机姿态可以被较精确地定位, 重建精度明显提高, 因此本文算法适用于对重建精度和实时性能要求较高的大规模场景的实时三维重建。

	Figure Option View Download New Window
	图8 三种算法的相机姿态优化比较Fig.8 Comparison of three algorithms about optimization of camera pose

5 结束语

本文提出了一种基于全局相机姿态优化策略的实时三维重建算法, 在使用深度传感器获取目标场景信息的同时完成了在线大规模场景的鲁棒重建。使用SIFT捆绑调整策略实现了本地与全局目标姿态的精准对齐, 同时使用动态优化策略对扫描到的帧数据进行实时优化重建, 保证了大规模场景的重建精度, 同时使用融合和去融合算法实现对三维场景的在线更新渲染重建。本文算法对大规模场景的重建精度较高, 相当于离线重建水平, 同时保证了重建速度, 是一种适用于大规模场景重建的在线算法。本文算法的在线三维重建速率为415 ms/帧, ICP姿态平均估计次数为20次, 传感器姿态变换的时间为100.0 ms, 可用于机器人视觉系统的信息获取、人工智能和虚拟现实领域以及对实时性要求较高的三维重建过程。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Weise T, Wismer T, Leibe B, et al. In-hand scanning with online loop closure[C]∥IEEE International Conference on Computer Vision Workshops, Kyoto, Japan, 2009: 1630-1637. [本文引用:1]
[2]	Henry P, Krainin M, Herbst E, et al. RGB-D mapping: using depth cameras for dense 3D modeling of indoor environments[J]. International Journal of Robotics Research, 2012, 31(5): 647-663. [本文引用:1]
[3]	Keller M, Lefloch D, Lambers M, et al. Real-time 3D reconstruction in dynamic scenes using point-based fusion[C]∥International Conference on 3D Vision-3DV, Tokyo, Japan, 2013, 8768(2): 1-8. [本文引用:1]
[4]	Whelan T, Leutenegger S, Salas-moreno R F, et al. Elastic fusion: dense SLAM without a pose graph[J/OL]. [2017-02-10]. http://www.doc.ic.ac.uk/~bglocker/pdfs/whelan2015rss.pdf. [本文引用:1]
[5]	Merrell P, Akbarzadeh A, Wang L, et al. Real-time visibility based fusion of depth maps[C]∥IEEE International Conference on Computer Vision, Rio de Janeiro, Brazil, 2007: 1-8. [本文引用:1]
[6]	Meilland M, Comport A. On unifying key-frame and voxel-based dense visual SLAM at large scales[C]∥International Conference on Intelligent Robots & Systems, Tokyo, Japan, 2013: 3677-3683. [本文引用:1]
[7]	Gallup D, Pollefeys M, Frahm J M. 3D reconstruction using an n-layer heightmap[J]. Pattern Recognition, 2010, 6376: 1-10. [本文引用:1]
[8]	Wurm K M, Hornung A, Bennewitz M, et al. Octomap: a probabilistic, flexible, and compact 3D map representation for robotic systems[J/OL]. [2017-02-13]. http://ais.informatik.uni-freiburg.de/publications/papers/wurm10octomap.pdf. [本文引用:1]
[9]	Curless B, Levoy M. A volumetric method for building complex models from range images[C]∥Conference on Computer Graphics and Interactive Techniques, New Orleans, LA, USA, 1996: 303-312. [本文引用:1]
[10]	Kornuta T, Laszkowski M. Perception subsystem for object recognition and pose estimation in RGB-D images[J]. Automation, Springer International Publishing, 2016, 44(10): 995-1003. [本文引用:1]
[11]	Steinbruecker F, Sturm J, Cremers D. Volumetric 3D mapping in real-time on a CPU[C]∥IEEE International Conference on Robotics and Automation, Stockholm, Sweden, 2014: 2021-2028. [本文引用:1]
[12]	Zollhöfer M, Thies J, Colaianni M, et al. Interactive model-based reconstruction of the human head using an RGB-D sensor[J]. Computer Animation & Virtual Worlds, 2014, 25(3-4): 213-222. [本文引用:1]
[13]	Zhou Q Y. Koltun V. Color map optimization for 3D reconstruction with consumer depth cameras[J]. ACM Transactions on Graphics, 2014, 33(4): 1-10. [本文引用:1]
[14]	Choi S, Zhou Q Y, Koltun V. Robust reconstruction of indoor scenes[C]∥IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 2015: 5556-5565. [本文引用:1]
[15]	Wikowski A, Kornuta T, Stefańczyk M, et al. Efficient generation of 3D surfel maps using RGB-D sensors[J]. International Journal of Applied Mathematics & Computer Science, 2016, 26(1): 99-122. [本文引用:1]
[16]	Newcombe R A, Izadi S, Hilliges O, et al. KinectFusion: real-time dense surface mapping and tracking[C]∥Conference on Computer Graphics & Interactive Techniques, New Orleans, LA, USA, 1996: 303-312. [本文引用:1]
[17]	Whelan T, Johannsson H, Kaess M, et al. Robust real-time visual odometry for dense RGB-D mapping[C]∥IEEE International Conference on Robotics and Automation, Karlsruhe, Germany, 2013: 13851317. [本文引用:1]
[18]	Lin J H, Wang Y J, Sun H H. A Feature-adaptive subdivision method for real-time 3D reconstruction of repeated topology surfaces[J]. 3D Research, 2017, 8(1): 1-16. [本文引用:1]
[19]	王新华, 欧阳继红, 张广, 等. 微扫描红外成像超分辨重建[J]. 吉林大学学报: 工学版, 2017, 47(1): 235-241. Wang Xin-hua, Ouyang Ji-hong, Zhang Guang, et al. Super-resolution reconstruction of infrared images based on micro-scanner[J]. Journal of Jilin University(Engineering and Technology Edition), 2017, 47(1): 235-241. [本文引用:1]
[20]	刘迎, 王朝阳, 高楠, 等. 特征提取的点云自适应精简[J]. 光学精密工程, 2017, 25(1): 245-254. Liu Ying, Wang Chao-yang, Gao Nan, et al. Point cloud adaptive simplification of feature extraction[J]. Optics and Precision Engineering, 2017, 25(1): 245-254. [本文引用:1]
[21]	张雷, 王延杰, 孙宏海, 等. 采用核相关滤波器的自适应尺度目标跟踪[J]. 光学精密工程, 2016, 24(2): 448-459. Zhang Lei, Wang Yan-jie, Sun Hong-hai, et al. Adaptive scale object tracking with kernelized correlation filters[J]. Optics and Precision Engineering, 2016, 24(2): 448-459. [本文引用:1]
[22]	王慧利, 朱明, 蔺春波, 等. 光学遥感图像中复杂海背景下的舰船检测[J]. 光学精密工程, 2018, 26(3): 723-732. Wang Hui-li, Zhu Ming, Lin Chun-bo, et al. Ship detection of complex sea background in optical remote sensing images[J]. Optics and Precision Engineering, 2018, 26(3): 723-732. [本文引用:1]
[23]	李湘眷, 王彩玲, 李宇, 等. 窗口融合特征对比度的光学遥感目标检测[J]. 光学精密工程, 2016, 24(8): 2067-2077. Li Xiang-juan, Wang Cai-ling, Li Yu, et al. Optical remote Sensing object detection based on fused feature Contrast of subwindows[J]. Optics and Precision Engineering, 2016, 24(8): 2067-2077. [本文引用:1]
[24]	徐伟, 陈彦彤, 朴永杰, 等. 基于吉林一号遥感图像的星载目标快速识别系统[J]. 光学精密工程, 2017, 25(1): 255-262. Xu Wei, Chen Yan-tong, Piao Yong-jie, et al. Target fast matching recognition of on-board system based on Jilin-1 satellite image[J]. Optics and Precision Engineering, 2017, 25(1): 255-262. [本文引用:1]

2009

0.0

... 三维重建方法使用多传感器获取底层数据信息,包括使用点数据信息融合的表示方式^[1,2,3,4]、2 ...

2012

0.0

... 三维重建方法使用多传感器获取底层数据信息,包括使用点数据信息融合的表示方式^[1,2,3,4]、2 ...

2013

0.0

... 三维重建方法使用多传感器获取底层数据信息,包括使用点数据信息融合的表示方式^[1,2,3,4]、2 ...

2017

0.0

... 三维重建方法使用多传感器获取底层数据信息,包括使用点数据信息融合的表示方式^[1,2,3,4]、2 ...

2007

0.0