柴油机主-从双微元Urea-SCR系统非线性状态观测器设计与分析

引用本文

宫洵, 蒋冰晶, 胡云峰, 曲婷, 陈虹. 柴油机主-从双微元Urea-SCR系统非线性状态观测器设计与分析[J].吉林大学学报（工学版）, 2018,48(4): 1055-1062
GONG Xun, JIANG Bing-jing, HU Yun-feng, QU Ting, CHEN Hong. Design and analysis of nonlinear state observer for master-slave two cell Urea-SCR system of diesel engine[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(4): 1055-1062 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20171213
Permissions

柴油机主-从双微元Urea-SCR系统非线性状态观测器设计与分析

宫洵^1,^2,³, 蒋冰晶^1,², 胡云峰^1,², 曲婷¹, 陈虹^1,²

1.吉林大学汽车仿真与控制国家重点实验室,长春130022

2.吉林大学通信工程学院,长春 130022

3.密歇根大学安娜堡分校机械工程学院,安娜堡 48109

通讯作者:曲婷(1982-),女,讲师,博士.研究方向:汽车动力系统控制及驾驶员行为建模.E-mail:qut@jlu.edu.cn

作者简介:宫洵(1988-),男,在站博士后.研究方向:发动机建模与控制.E-mail:gongxun10@hotmail.com

基金:国家自然科学基金项目(61703177); 吉林省教育厅项目(JJKH20170801KJ); 吉林省科技厅项目(20170520067JH,20180520200JH).

摘要

针对Urea-SCR状态反馈控制系统存在不可测状态变量的问题,首先,分析了SCR系统的化学反应机理,为了描述SCR系统的分布参数特性,给出了包含上游-下游(主-从)两个单元的SCR系统双核动力学模型;其次,利用Urea-SCR系统下游氨浓度及氮氧化物浓度的测量值,设计了非线性降维观测器估计上游氨浓度、上下氨覆盖率等不可测的状态变量,同时在Lyapunov稳定性框架下,分析了观测器的稳定性,并据此给出了保证观测器稳定的观测器增益的取值范围;最后,在发动机动力学仿真软件enDYNA中,通过FTP75循环测试工况仿真测试,验证了该方法的有效性。

关键词: 动力机械工程; 柴油发动机; 选择催化还原控制系统; 非线性观测器; 稳定性分析

中图分类号:TK411 文献标志码:A 文章编号:1671-5497(2018)04-1055-08

Design and analysis of nonlinear state observer for master-slave two cell Urea-SCR system of diesel engine

GONG Xun^1,^2,³, JIANG Bing-jing², HU Yun-feng^1,², QU Ting¹, CHEN Hong^1,²

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.Department of Control Science and Engineering,Jilin University, Changchun 130022, China

3.Department of Aerospace Engineering,Michigan University,Ann Arbo 48109,USA

Abstract

As one of the effective approaches to reduce NO _x emission of diesel, Urea Selective Catalytic Reduction (Urea-SCR) can catalytically convert toxic NO _x emission to nitrogen and water by accurately controlling the amount of ammonia injection. However, there still exists problem such as non-measurable states in Urea-SCR. To resolve this problem in the Urea-SCR feedback control system, first, the chemical reaction mechanism of DCR system is analyzed and a model containing both upstream and downstream (master-slave) elements is introduced. Second, a nonlinear reduced-order observer is designed to observe the non-measurable states by utilizing the concentration measurement downstream ammonia and NO _x, meanwhile, the stability of the observer is analyzed and the value range of the observer parameter is calculated based on stability analysis. Finally, the effectiveness of the proposed approach is testified by simulation in enDYNA employing FTP75 cycle test procedure.

Keyword: power machinery engineering; diesel engine; SCR control system; nonlinear observer; stability analysis

文章图片

0 引言

由于柴油发动机比汽油发动机具有更好的动力性与燃油经济性, 这使得柴油发动机在中/重型车辆中占有统治地位, 并在轻型车领域快速扩张^[1]。但是由于柴油机采用稀燃的方式导致其尾气中含有大量的氮氧化物(NO_x)^{[2, 3]}。为了减少NO_x对环境的污染, 研究人员提出了尾气后处理技术, 其中Urea-SCR尾气后处理技术由于成本较低且转化效率高, 得到了广泛应用。该技术利用氨(NH₃)将柴油机尾气中的NO_x还原为N₂与H₂O, 其中NH₃是由浓度为32.5%尿素溶液(俗称” 添蓝” )分解产生。

柴油发动机Urea-SCR控制系统的目标是使NO_x的排放量满足排放法规要求, 同时尽量避免有异味的NH₃逃逸, 目前投入市场的Urea-SCR系统主要以开环控制策略为主, 该方法具有逻辑简单, 工程实现方便等优点^{[4, 5]}, 但是无法满足国五排放标准对NO_x排放量的要求, 为此研究人员提出了一种基于NH₃覆盖率的Urea-SCR系统的闭环控制方法。该方法首先以NO_x的转化率为目标, 以NH₃的逃逸率为约束, 离线优化出满足性能指标及约束的NH₃覆盖率的期望值, 进一步通过NH₃的覆盖率的跟踪控制实现发动机的排放要求^{[4, 5, 6, 7]}。文献 [4, 5]中基于Urea-SCR系统的集中参数模型, 采用基于模型的NH₃覆盖率控制器设计方法, 实现了NH₃覆盖率的闭环控制。但对于商用车中使用的拥有较大尺寸的Urea-SCR系统, 由于系统上游-下游状态变量的差异比较大, 如果继续使用集中参数模型去设计控制器, 难以满足Urea-SCR系统的控制需求。针对上述问题, 文献[6, 7]建立了包含上游-下游(主-从)两个微元的Urea-SCR模型, 并采用反步法等非线性控制方法设计NH₃覆盖率跟踪控制器, 达到了较好的控制效果。

Urea-SCR系统的闭环控制策略虽然能够提高系统的控制效果, 但是由于所设计的控制器均是状态反馈控制器, 需要对状态变量进行实时测量, 而实际产品中由于成本等约束, 现有的Urea-SCR系统产品中只在后处理系统的尾部(下游)安装了NH₃和NO_x浓度传感器。因此需要设计观测器估计NH₃覆盖率等不可测的状态变量。目前, 针对集中参数NH₃覆盖率跟踪控制系统, 文献[7, 8, 9]设计了非线性观测器对NH₃覆盖率及NH₃浓度进行了估计; 文献[10]采用扩展Kalman滤波对NH₃覆盖率和NO_x浓度分别进行了估计。针对包含上游-下游两个微元的Urea-SCR系统, 文献[11]中设计全维滑模观测器对上游、下游NH₃的浓度及覆盖率进行了估计, 但其在估计过程中忽略了NO_x浓度对上述变量估计效果的影响。文献[12]对Urea-SCR下游NO_x浓度、NH₃的浓度及排气处NO_x的浓度进行测量, 对上游、下游NH₃的浓度及覆盖率进行了估计。本文针对包含上游-下游两个微元的Urea-SCR系统, 以下游NO_x浓度、NH₃浓度为测量值, 设计了非线性降阶观测器对上游NO_x浓度、NH₃浓度、NH₃覆盖率及下游NH₃覆盖率进行了估计, 并在Lyapunov稳定性的框架下证明了观测器误差系统的渐近稳定性, 并据此给出了观测器增益的选取范围; 最后在FTP75工况下, 通过Simulink仿真实验对其有效性进行了验证。

1 Urea-SCR系统建模

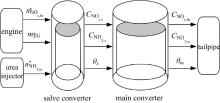
Urea-SCR系统利用尿素分解产生的NH₃作为还原剂, 将柴油发动机中的NO_x还原为H₂O、N₂, 从而达到减少柴油机尾气中NO_x排放的目的。在上述过程中会发生一系列复杂的化学反应, 其中主要包括尿素水溶液的分解、NH₃的吸附与解吸附、选择性催化还原反应以及NH₃的氧化反应, 具体的反应原理如图1所示。

	Figure Option View Download New Window
	图1 Urea-SCR化学反应示意图Fig.1 Schematic presentation of the Urea-SCR reaction

在Urea-SCR系统中, NH₃的浓度、NO_x的浓度及NH₃的覆盖率都是沿催化器的轴向及径向变化的状态变量, 是典型的分布参数式系统。本文为了简化Urea-SCR模型, 在建模过程中, 将Urea-SCR系统沿轴向分成上游和下游两个单元进行建模, 如图2所示。如果将Urea-SCR系统分为上游、下游两个单元, 其中第一个单元输出的NO_x浓度、NH₃浓度及NH₃的覆盖率作为下游的输入, 就可以得到上游-下游两个单元的Urea-SCR模型, 其中上游和下游的体积比例为1∶ 2。

	Figure Option View Download New Window
	图2 上游-下游U-SCR系统结构图Fig.2 Upstream-downstream structure diagram of U-SCR system

关于包含上游-下游两个单元的Urea-SCR的建模问题已经得到广泛的研究, 具体建模过程可参见文献[6, 7], 本文直接给出系统的动力学模型如下所示:

$\{\begin{array}{l} {\overset{\cdot}{C}}_{N O_{x}, i} = f_{1 i} (n_{N O_{x}, in, i}, C_{N O_{x}, i}, θ_{N H_{3}, i}) \\ {\overset{\cdot}{C}}_{N H_{3}, i} = f_{2 i} (n_{N H_{3}, in, i}, C_{N H_{3}, i}, θ_{N H_{3}, i}) \\ {\overset{\cdot}{θ}}_{N H_{3}, i} = f_{3 i} (C_{N O_{x}, i}, C_{N H_{3}, i}, θ_{N H_{3}, i}) \end{array}$ (1)

式中:下标 $i = d$ 代表下游的状态变量, 下标 $i = u$ 代表上游的状态变量。 $f_{1 i} f_{2 i}, f_{3 i}$ 的具体形式, 如式(2)所示:

$\{\begin{array}{l} f_{1 i} = a_{1 i} n_{x, in, i}^{*} - C_{N O_{x}, i} (a_{0} a_{1 i} m_{EG}^{*} T_{i} + a_{5 i} (T_{i}) θ_{N H_{3}, i}) \\ f_{2 i} = a_{1 i} n_{N H_{3}, in, i}^{*} - C_{N H_{3}, i} (a_{0} a_{1 i} m_{EG}^{*} T_{i} + \\ a_{3 i} (T_{i}) (1 - θ_{N H_{3}, i})) + a_{4 i} (T_{i}) θ_{N H_{3}, i} \\ f_{3 i} = (a_{3 i} (T_{i}) (1 - θ_{N H_{3}, i}) C_{N H_{3}, i} - (a_{4 i} (T_{i}) + \\ a_{5 i} (T_{i}) C_{N O_{x}, i} + a_{6 i} (T_{i}) θ_{N H_{3}, i}) / c_{s} \end{array}$ (2)

其中, 建模过程中所使用的常量及变量如表1、2所示。

表1 常量命名法 Table 1 Constants nomendature

符号	描述	数值	单位
$S_{C}$	1mol活性原子的表面积	581	m²/mol
α _prob	粘着率	1.11e-3	-
$c_{s}$	单位体积气体中活性原子浓度	7.30	mol/m³
c_p_{, EG}	排气定压比热	1060	J/(kg· K)
$c_{p, c}$	催化器比热	1054	J/(kg· K)
$M_{N H_{3}}$	NH₃的摩尔质量	17	g/mol
$R$	气体常数	8.3145	J/(mol· K)
$R_{S, EG}$	排气气体常数	288	J/(kg· K)
k_Des	解吸附速率因子	0.514	1/s
k_SCR	urea-SCR反应速率因子	2.6776	m²/s
$k_{O_{X}}$	NH₃氧化反应速率因子	3.34e6	1/s
$E_{a, Des}$	解吸附活性能	15.2	J/mol
$E_{a, SCR}$	urea-SCR反应活性能	28471	J/mol
$E_{a, O_{X}}$	NH₃氧化反应活性能	1.16e5	J/mol
P_amb	大气压	101325	Pa
$V_{c, i}$	urea-SCR系统上/ 下游容积	0.0033/0.0067	m³
$m_{c}$	催化器质量	19	kg
$ε$	空隙比	0.81	-
ε _{rad, scr}	黑度	0.507	-
$k \geq \frac{k_{1} y_{2}}{D_{3}}$	气体辐射常数	$k_{1} \geq 0$
$L_{3}$	催化器辐射表面积	0.9044	m²

表1 常量命名法 Table 1 Constants nomendature

表2 变量命名法 Table 2 Variables nomendature

符号	描述	单位
$x_{3} = C_{N O_{x, u}}$	物质x的摩尔浓度	mol/m³
$n_{X}^{*}$	物质x的摩尔质量流量	mol/s
$n_{N O_{x}, in}^{*}$	废气质量流量	kg/s
T, T_in, T_amb	温度, 废气温度, 环境温度	K
$θ_{N H_{3}}$	NH₃的表面覆盖率	-

表2 变量命名法 Table 2 Variables nomendature

2 非线性观测器的设计

在使用Urea-SCR模型设计反馈控制器时, 需要对Urea-SCR系统上下游的状态变量的测量值作为反馈信息。但出于成本考虑, 现有的Urea-SCR系统产品中只对Urea-SCR系统下游(出口处)NO_x浓度及NH₃浓度进行测量; 因此需要设计观测器对上游NO_x浓度, NH₃浓度, NH₃覆盖率及下游NH₃覆盖率进行估计:

定义 $x_{1} = C_{N H_{3, u}}, x_{2} = θ_{u}, x_{3} = C_{N O_{x, u}}, x_{4} = θ_{d},$ 表示不可测的状态变量, 定义 $y_{1} = C_{N H_{3, d}}, y_{2} = C_{N O_{x, d}}$ 表示可测的状态变量, 则由式(1)、(2)可以得到系统的动力学方程如下所示:

$\begin{array}{l} \{\begin{array}{l} {\overset{\cdot}{x}}_{1} = (- A_{1} + A_{2}) x_{1} - A_{2} x_{1} x_{2} + A_{3} x_{2} + a_{11} n_{N H_{3, in}} \\ {\overset{\cdot}{x}}_{2} = B_{1} x_{1} - B_{1} x_{1} x_{2} - B_{2} x_{2} - B_{3} x_{2} x_{3} \\ {\overset{\cdot}{x}}_{3} = - C_{1} x_{3} - C_{2} x_{2} x_{3} + a_{11} n_{N O_{x, in}} \\ {\overset{\cdot}{x}}_{4} = D_{1} y_{1} - D_{1} y_{1} x_{4} - D_{2} x_{4} - D_{3} y_{2} x_{4} \\ {\overset{\cdot}{y}}_{1} = E_{1} x_{1} - (E_{2} + E_{3}) y_{1} + E_{2} x_{4} y_{1} + E_{4} x_{4} \\ {\overset{\cdot}{y}}_{2} = F_{1} x_{3} - F_{2} y_{2} - F_{3} x_{4} y_{2} \end{array} \end{array}$ (3)

式中: $n_{N O_{x, in}}$ 、 $n_{N H_{3, in}}$ 分别表示发动机产生的NO_x及添蓝产生的NH_x, 其单位为mol/s; $A_{i} 、 B_{i} 、 C_{i} 、 D_{i} 、 E_{i} 、 F_{i} (i = 1, 2, 3, 4$ )是由式(2)中相关参数经过等量变换得到的, 其等量关系为:

$\begin{array}{l} A_{1} = a_{0} a_{1, 2} m_{EG} T_{2}, A_{2} = - a_{3, 2} (T_{2}), \\ A_{3} = a_{4, 2} (T_{2}), B_{1} = \frac{a_{3, 2} (T_{2})}{c_{s}}, \\ B_{2} = \frac{a_{4, 2} (T_{2}) + a_{6, 2} (T_{2})}{c_{s}}, B_{3} = \frac{a_{5, 2} (T_{2})}{c_{s}}, \\ C_{1} = a_{0} a_{1, 2} m_{EG} T_{2}, C_{2} = - a_{5, 2} (T_{2}), \\ D_{1} = \frac{a_{3, 1} (T_{1})}{c_{s}}, D_{2} = \frac{a_{6, 1} (T_{1}) + a_{4, 1} (T_{1})}{c_{s}}, \\ D_{3} = \frac{a_{5, 1} (T_{1})}{c_{s}}, E_{1} = a_{0} a_{1, 2} m_{EG} T_{2}, \\ E_{2} = a_{3, 1} (T_{1}), E_{3} = a_{0} a_{1, 1} m_{EG} T_{1}, \\ E_{4} = a_{4, 1} (T_{1}), F_{1} = a_{0} a_{1, 2} m_{EG} T_{2}, \\ F_{2} = a_{0} a_{1, 1} m_{EG} T_{1}, F_{3} = a_{5, 1} (T_{1}) \end{array}$

上述公式中:

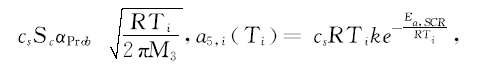
其中, 下标 $i = 2$ 代表Urea-SCR系统上游的参数, 下标 $i = 1$ 代表Urea-SCR系统下游的参数。

针对系统(3)的状态变量估计问题, 由于系统存在可测状态变量, 本文设计非线性降维观测器对主-从微元中不可测的状态变量 $x_{i}$ 进行估计, 可以有效降低观测器系统计算量。

因为上游NH₃的浓度、NH₃的覆盖率及下游NH₃的覆盖率直接影响下游NH₃浓度, 所以本文在估计 $x_{1} 、 x_{2}$ 及 $x_{4}$ 时选择 $y_{1}$ 作为矫正变量; 而上游NO_x的浓度则直接影响下游NO_x的浓度, 所以本文在估计 $x_{3}$ 时, 选择 $y_{2}$ 作为矫正变量, 具体的观测器的形式如下所示:

$\{\begin{array}{l} {\overset{\cdot}{\hat{x}}}_{1} = (- A_{1} + A_{2}) {\hat{x}}_{1} - A_{2} {\hat{x}}_{1} {\hat{x}}_{2} + A_{3} {\hat{x}}_{2} + a_{11} n_{N H_{3, in}} \\ + L_{1} [{\overset{\cdot}{y}}_{1} - (E_{1} {\hat{x}}_{1} - (E_{2} + E_{3}) y_{1} + \\ E_{2} {\hat{x}}_{4} y_{1} + E_{4} {\hat{x}}_{4})] \\ {\overset{\cdot}{\hat{x}}}_{2} = B_{1} {\hat{x}}_{1} - B_{1} {\hat{x}}_{1} {\hat{x}}_{2} - B_{2} {\hat{x}}_{2} - B_{3} {\hat{x}}_{2} {\hat{x}}_{3} + \\ L_{2} [{\overset{\cdot}{y}}_{1} - (E_{1} {\hat{x}}_{1} - (E_{2} + E_{3}) y_{1} + \\ E_{2} {\hat{x}}_{4} y_{1} + E_{4} {\hat{x}}_{4})] \\ {\overset{\cdot}{\hat{x}}}_{3} = - C_{1} {\hat{x}}_{3} - C_{2} {\hat{x}}_{2} {\hat{x}}_{3} + a_{11} n_{N O_{x}, in} + \\ L_{3} [{\overset{\cdot}{y}}_{2} - (F_{1} {\hat{x}}_{3} - F_{2} y_{2} - F_{3} {\hat{x}}_{4} y_{2})] \\ {\overset{\cdot}{\hat{x}}}_{4} = D_{1} y_{1} - D_{1} y_{1} {\hat{x}}_{4} - D_{2} {\hat{x}}_{4} - D_{3} {\hat{x}}_{4} y_{2} + \\ L_{4} [{\overset{\cdot}{y}}_{1} - (E_{1} {\hat{x}}_{1} - (E_{2} + E_{3}) y_{1} + \\ E_{2} {\hat{x}}_{4} y_{1} + E_{4} {\hat{x}}_{4})] \end{array}$ (4)

式中: ${\hat{x}}_{1} 、 {\hat{x}}_{2} 、 {\hat{x}}_{3} 、 {\hat{x}}_{4}$ 分别为状态变量 $x_{1} 、 x_{2} 、 x_{3} 、 x_{4}$ 的估计值; $L_{1} 、 L_{2} 、 L_{3} 、 L_{4}$ 代表观测器的增益。因为状态变量的估计值可能超出物理约束, 式(5)(6)通过定义不连续投影使估计值满足物理约束。

${\hat{x}}_{i} = \{\begin{array}{l} 0, {\hat{x}}_{i} \leq 0 \\ {\hat{x}}_{i}, others \end{array} i = 1, 3$ (5)

${\hat{x}}_{i} = \{\begin{array}{l} 0, {\hat{x}}_{i} \leq 0 \\ 1, {\hat{x}}_{i} \geq 1 \\ {\hat{x}}_{i}, others \end{array} i = 2, 4$ (6)

定义状态变量 $x_{1} 、 x_{2} 、 x_{3} 、 x_{4}$ 的估计误差:

$\{\begin{array}{l} e_{1} = x_{1} - {\hat{x}}_{1} \\ e_{2} = x_{2} - {\hat{x}}_{2} \\ e_{3} = x_{3} - {\hat{x}}_{3} \\ e_{4} = x_{4} - {\hat{x}}_{4} \end{array}$ (7)

将式(3)(4)代入式(7)中可以得到估计误差具体的表达式, 如式(8)所示:

$\{\begin{array}{l} {\overset{\cdot}{e}}_{1} = - (- A_{1} - A_{2} + L_{1} E_{1} + A_{2} {\hat{x}}_{2}) e_{1} + \\ (A_{3} - A_{2} x_{1}) e_{2} - L_{1} (E_{2} y_{1} + E_{4}) e_{4} \\ {\overset{\cdot}{e}}_{2} = (B_{1} - B_{1} {\hat{x}}_{2} - L_{2} E_{1}) e_{1} + (B_{1} x_{1} + B_{2} + \\ B_{3} {\hat{x}}_{3}) e_{2} - B_{3} x_{2} e_{3} - L_{2} (E_{4} + E_{2} y_{1}) e_{4} \\ {\overset{\cdot}{e}}_{3} = - C_{2} {\hat{x}}_{3} e_{2} + (C_{1} + C_{2} x_{2} + L_{3} F_{1}) e_{3} + \\ L_{3} F_{3} y_{2} e_{4} \\ {\overset{\cdot}{e}}_{4} = - L_{4} E_{1} e_{1} + (- D_{1} y_{1} - D_{2} - D_{3} y_{2} - \\ L_{4} (E_{4} y_{1} + E_{4})) e_{4} \end{array}$ (8)

定义误差系统的Lyapunov函数:

$V = \frac{1}{2} e_{1}^{2} + \frac{1}{2} e_{2}^{2} + \frac{1}{2} e_{3}^{2} + \frac{k}{2} e_{4}^{2}$ (9)

式中: $k$ 为一个大于零未知的参数。上式对时间求导, 得到Lyapunov函数对时间的导数:

$\overset{\cdot}{V} = e_{1} {\overset{\cdot}{e}}_{1} + e_{2} {\overset{\cdot}{e}}_{2} + e_{3} {\overset{\cdot}{e}}_{3} + k e_{4} {\overset{\cdot}{e}}_{4}$ (10)

把式(8)代入(10)中有:

$\begin{array}{l} \overset{\cdot}{V} = - (A_{1} - A_{2} + L_{1} E_{1} + A_{2} {\hat{x}}_{2}) e_{1}^{2} + \\ (A_{3} - A_{2} x_{1}) e_{1} e_{2} - \\ (L_{1} E_{4} + L_{1} E_{2} y_{1}) e_{1} e_{4} + \\ (B_{1} - B_{1} {\hat{x}}_{2} - L_{2} E_{1}) e_{1} e_{2} - \\ (B_{1} x_{1} + B_{2} + B_{3} {\hat{x}}_{3}) e_{2}^{2} - B_{3} x_{2} e_{2} e_{3} - \\ L_{2} (E_{2} y_{1} + E_{4}) e_{2} e_{4} - \\ C_{2} {\hat{x}}_{3} e_{2} e_{3} - (C_{1} + C_{2} x_{2} + L_{3} F_{1}) e_{3}^{2} + \\ L_{3} F_{3} y_{2} e_{3} e_{4} - k L_{4} E_{1} e_{1} e_{4} - \\ k (D_{1} y_{1} + D_{2} + D_{3} y_{2} + k L_{4} (E_{2} y_{1} + E_{4})) e_{4}^{2} \end{array}$ (11)

利用三角不等式 $a^{2} + b^{2} \geq 2 ab,$ 对(11)中的交叉相乘项 $k L_{4} E_{1} e_{1} e_{4} 、 (L_{1} E_{4} + L_{1} E_{2} y_{1}) e_{1} e_{4} 、 L_{3} F_{3} y_{2} e_{3} e_{4}$ 进行放大, 即可得到如下的不等式:

$\begin{array}{l} \{\begin{array}{l} E_{1}^{2} e_{1}^{2} + \frac{k^{2}}{4} L_{4}^{2} e_{4}^{2} \geq (k L_{4} E_{1}) e_{1} e_{4} \\ \frac{1}{4} L_{1}^{2} e_{1}^{2} + {(E_{2} y_{1} + E_{4})}^{2} e_{4}^{2} \geq (L_{1} (E_{2} y_{1} + E_{4})) e_{1} e_{4} \\ \frac{1}{4 k_{1}} {(L_{3} F_{3})}^{2} e_{3}^{2} + k_{1} y_{2}^{2} e_{4}^{2} \geq (L_{3} F_{3} y_{2}) e_{3} e_{4} \end{array} \end{array}$ (12)

式中: $k_{1}$ 是一个大于0的可调参数。由式(11)(12)可得:

$\begin{array}{l} \overset{\cdot}{V} \leq A_{2} (1 - {\hat{x}}_{2}) e_{1}^{2} + \\ (A_{3} - A_{2} x_{1} + B_{1} - B_{1} {\hat{x}}_{2} - L_{2} E_{1}) e_{1} e_{2} - \\ B_{1} x_{1} e_{2}^{2} - (k D_{3} y_{2} - \frac{k^{2}}{4} L_{4}^{2} + k L_{4} (E_{2} y_{1} + E_{4}) - \\ {(E_{2} y_{1} + E_{4})}^{2} - k_{1} y_{2}^{2}) e_{4}^{2} - \\ A_{1} e_{1}^{2} - (- E_{1}^{2} + L_{1} E_{1} - \frac{1}{4} L_{1}^{2}) e_{1}^{2} - \\ (C_{1} + C_{2} x_{2} + L_{3} F_{1} - \frac{1}{4 k_{1}} {(L_{3} F_{3})}^{2}) e_{3}^{2} - \\ (k D_{1} y_{1} + k D_{2}) e_{4}^{2} - (L_{2} E_{4} + L_{2} E_{2} y_{1}) e_{2} e_{4} - \\ (B_{2} + B_{3} {\hat{x}}_{3}) e_{2}^{2} - (C_{2} {\hat{x}}_{3} + B_{3} x_{2}) e_{2} e_{3} \end{array}$ (13)

其中令观测增益 $L_{4} 、 L_{1}$ 的值为:

$\{\begin{array}{l} L_{4} = \frac{2 (E_{2} y_{1} + E_{4})}{k} \\ L_{1} = 2 E_{1} \end{array}$ (14)

将式(12)代入式(11)中有:

$\begin{array}{l} \overset{\cdot}{V} \leq A_{2} (1 - {\hat{x}}_{2}) e_{1}^{2} - B_{1} x_{1} e_{2}^{2} + \\ (A_{3} - A_{2} x_{1} + B_{1} - B_{1} {\hat{x}}_{2} - L_{2} E_{1}) e_{1} e_{2} - \\ (k D_{3} y_{2} - k_{1} y_{2}^{2}) e_{4}^{2} - A_{1} e_{1}^{2} - \\ (L_{3} F_{1} - \frac{1}{4 k_{1}} {(L_{3} F_{3})}^{2} + C_{1} + C_{2} x_{2}) e_{3}^{2} - \\ (C_{2} {\hat{x}}_{3} + B_{3} x_{2}) e_{2} e_{3} - B_{2} e_{2}^{2} - \\ (k D_{1} y_{1} + k D_{2}) e_{4}^{2} - (L_{2} E_{4} + L_{2} E_{2} y_{1}) e_{2} e_{4} - \\ (B_{2} + B_{3} {\hat{x}}_{3}) e_{2}^{2} \end{array}$ (15)

为了保证观测器误差系统的Lyapunov函数的导数小于零, 需要满足式(16~19)成立, 即有状态变量的估计值收敛于其真实值。

$- 4 A_{2} (1 - {\hat{x}}_{2}) B_{1} x_{1} \geq (A_{3} - A_{2} x_{1} + B_{1} - B_{1} {\hat{x}}_{2} - {L_{2} E_{1})}^{2}$ (16)

$k D_{3} - k_{1} y_{2} \geq 0$ (17)

$4 (L_{3} F_{1} - \frac{1}{4 k_{1}} {(L_{3} F_{3})}^{2} + C_{1} + C_{2} x_{2}) \geq c_{2} {\hat{x}}_{3} + B_{3} x_{2}$ (18)

$4 (k D_{1} y_{1} + k D_{2}) (B_{3} {\hat{x}}_{3}) \geq {(L_{2} E_{4} + L_{2} E_{2} y_{1})}^{2}$ (19)

解不等式(16)~(19)得如下不等式:

$k \geq \frac{k_{1} y_{2}}{D_{3}}$ (21)

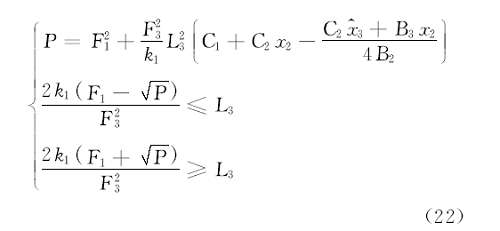
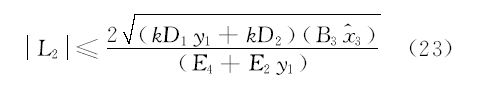式(20)中, $A_{2}$ 小于0, 且 ${\hat{x}}_{2} \in [0, 1],$ 即式(20)肯定成立; 另一方面, 式(23)中 $L_{2}$ 的取值范围与参数 $k$ 有关, 只要参数 $k$ 足够大, 式(20)与式(23)就能够同时成立。对于式(22), 只要 $P \geq 0$ 该式就能成立, 其成立的条件分为两种情况进行讨论:① $C_{1} + C_{2} x_{2} - \frac{C_{2} {\hat{x}}_{3} + B_{3} x_{2}}{4 B_{2}} \geq 0$ 时, 不管 $k_{1}$ 如何取值 $P \geq 0$ 肯定成立; ② $C_{1} + C_{2} x_{2} - \frac{C_{2} {\hat{x}}_{3} + B_{3} x_{2}}{4 B_{2}} < 0$ 时, 只要满足:

$k_{1} > \frac{F_{3}^{2} L_{3}^{2} (C_{1} + C_{2} x_{2} - \frac{C_{2} {\hat{x}}_{3} + B_{3} x_{2}}{- F_{1}^{2}})}{- F_{1}^{2}}$ (24)

$P \geq 0$ 成立, 所以当 $k_{1}$ 满足式(24)时, 式(22)成立。

通过以上分析可知式(20)~(23)同时成立时, 式(15)即Lyapunov函数小于等于零, 从而保证降阶观测器稳定。

通过上面的讨论可以看出为了保证Lyapunov函数的稳定性, 观测器增益需要满足式(20)~(23)与式(14)。在(21)~(23)中, $k_{1} \geq 0$ 和 $k \geq 0$ 是需要选定的参数, 现在给出它们以及观测器增益选择的具体步骤。

步骤1 首先选择 $k_{1},$ 使其同时满足 $k_{1} \geq 0$ 及式(22)。

步骤2 根据式(21)、式(20)及式(23)确定参数 $k 。$

步骤3 根据式(14)确定观察增益 $L_{1} 、 L_{4} 。$

步骤4 根据式(22)确定观测增益 $L_{3} 。$

步骤5 根据式(20)、(23)确定观测增益 $L_{2} 。$

因为在设计降维观测器的过程中使用到了NO_x浓度, NH₃浓度的微分信号, 所以本文使用了如(25)所示的跟踪微分器对下游NO_x浓度及NH₃的浓度的微分信号进行提取:

$\{\begin{array}{l} {\overset{\cdot}{v}}_{1} = v_{2} \\ {\overset{\cdot}{v}}_{2} = - r^{2} (v_{1} - y) - 2 r v_{2} \end{array}$ (25)

式中: $v_{1} 、 v_{2} 分别为测量值 y$ 的重构量及其微分的重构量。

3 仿真分析

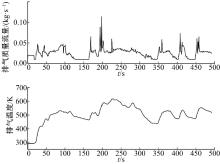
本文使用FTP75瞬态工况通过仿真实验对上述降维观测器的估计性能进行分析, FTP75工况如图3、图4所示。在仿真过程中, 考虑以下两个方面对于观测器估计性能的影响:①在实际过程中, 每个微元中的温度不可能是均匀分布的而且温度对Urea-SCR模型中化学反应速率有着直接的影响, 这将导致Urea-SCR模型中参数的不确定性。本文通过仿真实验, 分析了由于温度变化而导致的参数不确定性对观测器性能的影响; ②考虑到测量噪声对观测效果的影响, 本文在仿真过程中对NO_x的浓度及NH₃的浓度加入了测量噪声。

	Figure Option View Download New Window
	图3 工况(排气温度、排气质量流量)Fig.3 Working condition(exhaust temperature、 exhaust mass flow)

	Figure Option View Download New Window
	图4 工况(进气处NO_x/NH₃的浓度)Fig.4 Working condition(intake NO_x/NH₃ concetration)

在仿真实验过程中, 虽然 $A_{i} 、 B_{i} 、 C_{i} 、 D_{i} 、 E_{i} 、 F_{i}$ 是变化的, 但其变化范围可以通过实验确定。在确定上述参数的变化范围之后, 可以通过式 (20~23)确定一组滤波增益值。本文根据第3节的观测器增益选择步骤选取了一组 $L_{1} 、 L_{2} 、 L_{3} 、 L_{4}$ 具体的数值为:

$L_{3} = 200, L_{1} = 60, L_{2} = 3, L_{4} = 0.1$

本文主要考虑参数不确定性( $c_{s}$ 的变化)及测量噪声对观测器性能的影响。其中图5、图6给出的是实际系统与仿真模型的参数一致时, 上游NH₃浓度、NO_x浓度及上下游NH₃覆盖率估计效果图, 可以看出观测器的估计值能够很好地跟踪上实际值。图7给出了NH₃覆盖率估计值的相对估计误差, 其中上游NH₃覆盖率相对估计误差的最大值为5%左右; 下游NH₃覆盖率的相对估计误差的最大值为10%左右。图8、图9给出了当实际系统参数发生变化时, 上游NH₃浓度、NO_x浓度及上下游NH₃覆盖率估计效果图, 可以看出上游NH₃覆盖率的估计效果变差。由图10可知上游NH₃覆盖率相对估计误差的最大值增加到20%左右, 但其平均相对为误差5%左右; 实际系统参数的变化对下游NH₃覆盖率的估计效果没有太大影响, 其相对估计误差最大值保持在1%左右。

	Figure Option View Download New Window
	图5 c_s=7.3时上游NO_x/NH₃浓度的估计效果Fig.5 The estimation result of upstream NO_x/NH₃ concentration with c_s=7.3

	Figure Option View Download New Window
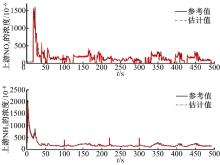
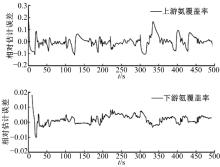
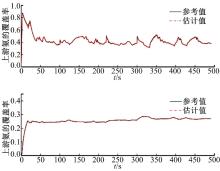	图6 c_s=7.3时上、下游氨覆盖率的估计效果Fig.6 The estimation of upstream and downstream ammonia coverage ratio with c_s=7.3

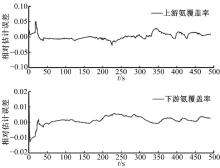	Figure Option View Download New Window
	图7 c_s=7.3时上、下游氨覆盖率的相对估计误差Fig.7 The relative estimation error of upstream and downstream ammonia coverage ratio with c_s=7.3

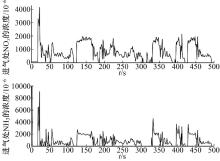
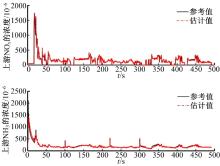	Figure Option View Download New Window
	图8 c_s=5.3时, 上游NO_x/NH₃浓度的估计效果Fig.8 The estimation result of upstream NO_x/NH₃ concentration with c_s=5.3

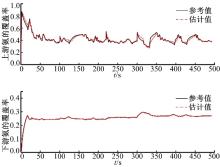	Figure Option View Download New Window
	图9 c_s=5.3时上、下游氨覆盖率的估计效果Fig.9 The estimation of upstream and downstream ammonia coverage ratio with c_s=5.3

	Figure Option View Download New Window
	图10 c_s=5.3时上、下游氨覆盖率的相对估计误差Fig.10 The relative estimation error of upstream and downstream ammonia coverage ratio with c_s=5.3

4 结束语

本文基于双微元的Urea-SCR系统, 利用Urea-SCR系统下游NO_x浓度及NH₃浓度的测量值设计了非线性降维观测器, 并在Lyapunov稳定性框架下证明了观测器误差系统的稳定性, 同时据此给出了观测器增益的取值范围。由仿真仿真实验可知, 该观测器能较好地估计上游NO_x的浓度、上游NH₃的浓度、上游NH₃覆盖率及下游NH₃覆盖率。另一方面, 本文设计的观测器与全维观测器相比, 降低了工程实现工程过程中在线计算的工作量, 有利于进一步的工程化应用。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	周庆辉. 现代汽车排放控制技术[M]. 北京: 北京大学出版社, 2010: 15-16. [本文引用:1]
[2]	杨成宏. 重型柴油机SCR催化器控制模型研究[D]. 长春: 吉林大学汽车工程学院, 2011. Yang cheng-hong. Study on the control model of SCR for heavy-duty diesel engine[D]. Changchun: College of Automotive Engineering, Jilin University, 2011. [本文引用:1]
[3]	汪立志. 柴油机Urea-SCR系统控制模型的设计与仿真研究[D]. 武汉: 武汉理工大学能源与动力工程学院, 2011. Wang Li-zhi. Design and simulation of the control model of urea-scr system in diesel engine[D]. Wuhan: College of Energy and Power Engineering, Wuhan University of Technology, 20011. [本文引用:1]
[4]	Upadhyay D, Van Nieuwstadt M. Model based analysis and control design of a urea-SCR deNO x aftertreatment system[J]. Journal of Dynamic Systems, Measurement, and Control, 2006, 128(3): 737-741. [本文引用:2]
[5]	Herman A, Wu M C, Cabush D, et al. Model based control of SCR dosing and OBD strategies with feedback from NH₃ sensors[J]. SAE International Journal of Fuels and Lubricants, 2009, 2(1): 375-385. [本文引用:2]
[6]	Hsieh M F, Wang J. A two-cell backstepping- based control strategy for diesel engine selective catalytic reduction systems[J]. IEEE Transactions on Control Systems Technology, 2011, 19(6): 1504-1515. [本文引用:1]
[7]	Zhao J, Hu Y, Gong X, et al. Modelling and control of urea-SCR systems through the triple-step non-linear method in consideration of time-varying parameters and reference dynamics[J]. Transactions of the Institute of Measurement and Control, 2018, 40(1): 287-302. [本文引用:2]
[8]	Zhang H, Wang J, Wang Y Y. Robust filtering for ammonia coverage estimation in diesel engine selective catalytic reduction systems[J]. Journal of Dynamic Systems, Measurement, and Control, 2013, 135(6): 064504. [本文引用:1]
[9]	Zhang H, Wang J, Wang Y Y. Nonlinear observer design of diesel engine selective catalytic reduction systems with NO _x sensor measurements[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(4): 1585-1594. [本文引用:1]
[10]	Hsieh M F, Wang J. Design and experimental validation of an extended Kalman filter-based NO _x concentration estimator in selective catalytic reduction system applications[J]. Control Engineering Practice, 2011, 19(4): 346-353. [本文引用:1]
[11]	Hsieh M F, Wang J. Sliding-mode observer for urea-selective catalytic reduction (SCR) mid-catalyst ammonia concentration estimation[J]. International Journal of Automotive Technology, 2011, 12(3): 321-329. [本文引用:1]
[12]	Zhang H, Wang J, Wang Y Y. Sensor reduction in diesel engine two-cell selective catalytic reduction (SCR) systems for automotive applications[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(5): 2222-2233. [本文引用:1]

2010

0.0

... 0 引言由于柴油发动机比汽油发动机具有更好的动力性与燃油经济性,这使得柴油发动机在中/重型车辆中占有统治地位,并在轻型车领域快速扩张^[1] ...

2011

0.0

. 2011, :-

Study on the control model of SCR for heavy-duty diesel engine

重型柴油机SCR催化器控制模型研究

Yang cheng-hong

杨成宏

随着人们对环境问题的关注,排放法规日益严格,对重型柴油机排放控制技术的研究具有重要意义。在欧洲,“优化燃烧+选择性催化还原(Selective Catalytic Reduction,简称SCR)”的排放控制技术以其燃油经济性好、抗硫中毒能力强等优点,已成为重型柴油机满足欧IV欧V排放标准的主流技术路线。在我国,随着国IV国V排放法规的推进,SCR技术也正在成为国内发动机排放技术研究的一大热点。为了提高SCR系统的控制性能,开发满足国V排放法规的SCR系统,本论文针对目前主流的SCR系统,从SCR催化器控制模型建立,参数辨识,实验验证和控制器设计四方面进行了深入的研究。针对SCR催化器三维建模复杂的特点,本文建立了适用于ECU实时计算的SCR催化器的一维分层模型。依据Eley-Rideal机理,结合稀燃柴油机的特点,确定了影响SCR反应动态过程的四个主要的化学反应——NH3的吸附及解吸附、NH3选择性催化还原反应及NH3的氧化反应。通过物质平衡方程,将以上化学反应过程进行了描述。基于能量守恒定律,推导了SCR分层模型中计算温度的方程,结合化学反应过程中的方程建立了SCR催化器的数学模型。针对分层模型微元个数的选取进行了比较分析,推荐了适用于SCR系统控制的微元个数选取原则。针对SCR催化器控制模型参数多,系统非线性强的特点,提出了基于非线性最小二乘法的模型参数辨识方法。为了保证辨识算法的收敛,对SCR模型对各参数的敏感性进行了仿真分析,确定了影响该模型响应特性的主导参数。针对法规要求和对模型动态性能准确性的要求,选取了参数辨识的实验工况,并实现了基于所选取实验工况的SCR催化器控制模型参数辨识。通过某重型柴油机系统台架对SCR催化器控制模型进行了实验验证。实验验证分为稳态实验和瞬态实验,在稳态实验中,针对发动机的主要工况点(包含所有ESC工况),分别进行了不同氨氮比下SCR反应特性的实验验证;在瞬态实验中,对ETC循环下的SCR反应特性进行了对比。实验结果表明,本文建立的SCR催化器控制模型对催化器的温度、化学反应速率、NH3泄漏等重要变量的预测都与实验相符,完全可以满足SCR控制器设计的需求。基于以上提出的SCR催化器控制模型,本文设计了基于模型的SCR系统前馈控制器,并利用SIMULINK仿真软件对其进行了仿真研究。仿真结果表明,因为基于模型的SCR控制策略考虑了SCR催化器内部反应的动态过程,所以相比基于脉谱图的传统SCR控制策略,它可以更好的控制系统的氨泄漏,在一定程度上改善在工况变化剧烈时SCR系统的控制性能。

... 但是由于柴油机采用稀燃的方式导致其尾气中含有大量的氮氧化物(NO_x)^[2,3] ...

2011

0.0

. 2011, :20011- DOI:doi:10.7666/d.y1880637

Design and simulation of the control model of urea-scr system in diesel engine

柴油机Urea-SCR系统控制模型的设计与仿真研究

Wang Li-zhi

汪立志

在机动车持续增长和能源紧缺的形势下,发展和完善发动机NOx控制技术对减少全球NOx排放有十分重要的意义。面对越来越严格的排放法规,在众多的排气后处理措施中Urea-SCR技术被认为是车用柴油机满足当前排放标准的最优选择。针对不同NOx排放水平的柴油机,快速开发出与之匹配的SCR后处理系统,已成为迫在眉睫的任务。 SCR系统的尿素喷射量控制策略确定后,需要经过有效的标定工作得到准确的控制参数,以保证SCR系统正常工作时柴油机排放达到法规标准。本文基于MATLAB/Simulink软件平台,建立柴油机SCR系统仿真模型。依据柴油机ETC循环NOx排放与NH3泄漏的仿真预测结果,实现柴油机SCR控制策略的优化与完善。主要研究内容为： (1)基于AVL BOOST软件平台,建立一维瞬态催化器模型,介绍了模型求解方法和模型参数优化计算方法；并借助AVL Design Explorer平台,选择遗传算法对SCR化学反应动力学参数进行优化,将优化后的计算结果与试验数据对比,表明优化后的参数提高了催化器模型的仿真性能。 (2)基于MATLAB/Simulink软件平台,建立SCR系统尿素喷射量控制模型,实现模型控制参数的在线修改和尿素喷射量的在线调整功能。通过计算排气中NOx对尿素溶液的理论需求量,结合尿素喷射量计算逻辑以及原机NOx排放、排气流量、转化效率等脉谱图,在MATLAB/Simulink软件平台建立SCR系统尿素喷射量控制模型。 (3)以MATLAB/Simulink软件为平台,在SCR系统尿素喷射量控制模型基础上,通过与AVL BOOST软件耦合计算,嵌入实时SCR催化化学反应模型,形成一个集系统输入信号、尿素喷射量控制系统、催化化学反应计算以及输出NOx排放值为一体的柴油机NOx排放预测模型。并提出和实践了一种较为先进的柴油机排放匹配标定方法：基于建立的仿真模型,依据柴油机ETC循环NOx排放与NH3泄漏的仿真预测结果,实现柴油机排放控制策略优化与完善。最后,通过试验验证了仿真模型的有效性。

... 但是由于柴油机采用稀燃的方式导致其尾气中含有大量的氮氧化物(NO_x)^[2,3] ...

2006

0.0

... 柴油发动机Urea-SCR控制系统的目标是使NO_x的排放量满足排放法规要求, 同时尽量避免有异味的NH₃逃逸,目前投入市场的Urea-SCR系统主要以开环控制策略为主,该方法具有逻辑简单,工程实现方便等优点^[4,5],但是无法满足国五排放标准对NO_x排放量的要求,为此研究人员提出了一种基于NH₃覆盖率的Urea-SCR系统的闭环控制方法 ...

... 该方法首先以NO_x的转化率为目标,以NH₃的逃逸率为约束,离线优化出满足性能指标及约束的NH₃覆盖率的期望值,进一步通过NH₃的覆盖率的跟踪控制实现发动机的排放要求^[4,5,6,7] ...

2009

0.0

2011

0.0

2018

0.0

... 目前,针对集中参数NH₃覆盖率跟踪控制系统,文献[7,8,9]设计了非线性观测器对NH₃覆盖率及NH₃浓度进行了估计 ...

2013

0.0

... 目前,针对集中参数NH₃覆盖率跟踪控制系统,文献[7,8,9]设计了非线性观测器对NH₃覆盖率及NH₃浓度进行了估计 ...

2015

0.0

... 目前,针对集中参数NH₃覆盖率跟踪控制系统,文献[7,8,9]设计了非线性观测器对NH₃覆盖率及NH₃浓度进行了估计 ...

2011

0.0

... 文献[10]采用扩展Kalman滤波对NH₃覆盖率和NO_x浓度分别进行了估计 ...

2011

0.0

... 针对包含上游-下游两个微元的Urea-SCR系统,文献[11]中设计全维滑模观测器对上游、下游NH₃的浓度及覆盖率进行了估计,但其在估计过程中忽略了NO_x浓度对上述变量估计效果的影响 ...

2015

0.0

... 文献[12]对Urea-SCR下游NO_x浓度、NH₃的浓度及排气处NO_x的浓度进行测量,对上游、下游NH₃的浓度及覆盖率进行了估计 ...