基于二次规划的分布式电动汽车稳定性控制

引用本文

金立生, 谢宪毅, 高琳琳, 郭柏苍. 基于二次规划的分布式电动汽车稳定性控制[J].吉林大学学报（工学版）, 2018,48(5): 1349-1359
JIN Li-sheng, XIE Xian-yi, GAO Lin-lin, GUO Bai-cang. Distributed electric vehicle stability control based on quadratic programming[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1349-1359 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170705
Permissions

基于二次规划的分布式电动汽车稳定性控制

金立生¹, 谢宪毅¹, 高琳琳², 郭柏苍¹

1.吉林大学交通学院,长春130022

2.常熟理工学院汽车工程学院,江苏常熟215500

作者简介:金立生(1975-),男,教授,博士生导师.研究方向:汽车安全与智能车辆导航技术.E-mail:jinls@jlu.edu.cn

基金:国家自然科学基金项目(51575229);国家重点研发计划项目(2016YFB0100900);中央高校基本科研业务费专项项目;吉林大学国家杰出青年基金后备人选培育计划项目

摘要

为了减少稳定性控制中车速降低程度,降低轮胎纵向力利用率,本文基于分布式电动汽车平台,通过二次规划的方法分配各个车轮所需的纵向力,优先基于轮毂电机输出驱动力/制动力来实现横摆力矩分配。当所需横摆力矩超过轮毂电机的最大转矩时,启动液压制动系统进行补偿。双移线试验仿真结果表明,相比于传统差动制动控制系统,基于二次规划的稳定性控制系统与理想车速之间的误差保持在1 km/h以内,车速降低82.25%,平均每个轮胎力纵向利用率下降9.71%。该稳定性控制系统能够提升车辆操控稳定性和安全性,并且在加速/减速工况下具有较好的鲁棒性。

关键词: 车辆工程; 分布式电动汽车; 二次规划; 横摆力矩分配; 操控稳定性

中图分类号:U461.1 文献标志码:A 文章编号:1671-5497(2018)05-1349-11

Distributed electric vehicle stability control based on quadratic programming

JIN Li-sheng¹, XIE Xian-yi¹, GAO Lin-lin², GUO Bai-cang¹

1.College of Transportation, Jilin University, Changchun 130022, China

2.College of Automobile Engineering, Changshu Institute of Technology, Changshu 215500,China

Abstract

In order to reduce the degree of speed reduction in the stability control and the longitudinal force utilization of the tires, the longitudinal force of each wheel is assigned by the secondary programming method based on the distributed electric vehicle platform. The yaw moment distribution based on the wheel motor output driving/braking force is preferred. When the required yaw moment exceeds the maximum torque of the wheel motors, the hydraulic brake system is activated to compensate. The results of Double Lane Change (DLC) simulation test demonstrate that, compared with the differential braking control system, the error between distributed electric vehicle stability control system and the ideal vehicle speed is kept within 1 km/h, the vehicle speed decreases by 82.25%, and the average tire force utilization rate is reduced by 9.71%. The stability control system can improve the stability and the safety of the driving vehicle. Under the acceleration/deceleration conditions, it provides good robustness.

Keyword: vehicle engineering; distributed electric vehicle; quadratic programming; distribution of yaw moment; handling stability

文章图片

0 引言

汽车稳定性控制系统是当前国际上汽车安全领域的研究热点^[1]。其中, 具有代表性的ESP^{[2, 3, 4]}、4WS^{[3, 4]}、AS^{[2, 4, 5, 6]}技术已经十分成熟。这些主动安全控制技术多用于内燃机汽车, 却也存在着显著的缺点。传统的内燃机汽车的结构决定了仅能依靠差动制动或主动转向的方式来产生维持稳定行驶的横摆力矩^[7], 当需要较大横摆力矩时, 必然消耗更多的轮胎纵向力, 降低了车辆稳定性裕度, 也降低了车速, 对车辆纵向行驶产生影响^[8]。某些工况下稳定性系统的频繁介入降低了车辆的操控性, 更无法兼顾驾驶员的驾驶意图。

目前, 分布式驱动电动汽车的优势已经愈加明显^{[9, 10]}。电机的转矩响应速度快、效率高^{[11, 12]}, 每个车轮的驱动/制动转矩独立可控, 为车辆动力学控制提供了更为多样化的解决方案。其制动力矩既能由轮毂电机来提供, 又可以依靠液压系统来提供^[13]。电机提供的制动力矩响应较快, 但是其峰值较低; 而液压系统提供的制动力矩峰值较大, 但响应具有滞后性。当电机峰值扭矩无法满足横摆力矩需求时, 依靠液压系统补偿^[14]。将轮毂电机与液压制动系统相结合, 充分发挥二者的优势, 互补不足。许多学者也就此展开了研究。文献[15]基于滑膜控制理论设计维持车辆稳定行驶的横摆力矩计算器, 通过单侧车轮驱动结合单侧车轮制动的方式来提高车辆的操纵稳定性。文献[16]以模糊控制理论与PID控制器相结合, 设计了基于轮毂电机的复合制动稳定性控制器, 充分发挥复合制动的优势并用以提升轮毂电机驱动的电动汽车在转弯工况下的稳定性。文献[17]以逻辑门限值控制方法和模糊控制方法对基于轮毂电机驱动的电动汽车驱动防滑控制进行研究, 有效限制了驱动车轮打滑现象。文献[18]设计了分层控制结构的轮毂电机稳定性控制器。上层控制器采用鲁棒控制理论中的 $μ$ 控制算法结合模型匹配方法设计控制系统结构, 决策稳定性控制所需求的横摆力矩; 下层控制器将横摆力矩以差动制动的形式进行分配。

以上研究以轮毂电机驱动的分布式电动汽车为依托, 设计了车辆稳定性控制器, 当车辆处于稳定状态时, 通过调节各个车轮的驱动/制动转矩实现横摆力矩的分配, 能够提升车辆的操控稳定性和动态响应性能。当车辆处于非稳定状态时, 依靠电机制动或液压复合制动也能够保证车辆不发生失稳, 取得了较好的控制效果。

针对车辆发生失稳的情况, 通常是因为某个车轮发生了轮胎力饱和现象^{[19, 20]}, 不能提供足够的侧向力, 进而导致车辆发生侧滑、失稳; 轮胎的纵向力利用率可以表征轮胎的稳定性裕度^{[21, 22]}, 在设计车辆稳定性控制器时, 应考虑这样的问题。控制轮胎力的利用率在合理范围内, 也是实现车辆稳定性控制的基础与根本。本文基于轮胎的利用率之和最小为优化目标, 通过滑膜控制理论设计横摆力矩计算器, 并根据二次规划理论设计横摆力矩分配器, 引入权重系数以优先满足稳定性控制的广义力约束。同时, 考虑电机输出转矩极限和路面附着条件的约束, 并加入一阶惯性环节表征驱动和制动系统的响应延迟现象。该控制策略能够降低汽车稳定性控制时轮胎纵向力利用率, 提升轮胎的稳定裕度, 也能够减少稳定性控制器对行驶车速的影响, 同时可在一定程度上兼顾驾驶员的意图。

1 车辆建模

根据达朗贝尔定理, 建立分布式电动汽车整车8自由度动力学模型^{[23, 24]}, 其中包括车辆纵向、侧向、横摆、侧倾自由度以及4个车轮的旋转自由度。

车辆动力学微分方程如下:

纵向运动:

$m ({\overset{\cdot}{v}}_{x} - w_{r} v_{y}) + m_{s} h_{s} w_{r} \overset{\cdot \cdot}{φ} =$

$F_{x fl} \cos δ - F_{y fl} \sin δ + F_{x fr} \cos δ -$

$F_{y fr} \sin δ + F_{x rl} + F_{x rr} (1)$

侧向运动:

$m ({\overset{\cdot}{v}}_{y} + w_{r} v_{x}) - m_{s} h_{s} \overset{\cdot \cdot}{φ} =$

$F_{x fl} \sin δ + F_{y fl} \cos δ + F_{x fr} \sin δ +$

$F_{y fr} \cos δ + F_{y rl} + F_{y rr} (2)$

横摆运动:

$I_{z} {\overset{\cdot}{w}}_{r} - I_{xz} \overset{\cdot \cdot}{φ} =$

$a (F_{x fl} \sin δ + F_{y fl} \cos δ + F_{x fr} \sin δ +$

$F_{y fr} \cos δ) - b (F_{y rl} + F_{y rr}) + \frac{d}{2} (F_{x fl} \cos δ -$

$F_{y fl} \sin δ + F_{x rl}) - \frac{d}{2} (F_{x fr} \cos δ - F_{y fr} \sin δ + F_{x rr}) (3)$

侧倾运动:

$I_{x} \overset{\cdot \cdot}{φ} - I_{xz} {\overset{\cdot}{w}}_{r} = m_{s} h_{s} ({\overset{\cdot}{v}}_{y} + v_{x} w_{r}) +$

$m_{s} h_{s} gφ - (K_{φ f} + K_{φ r}) φ - (C_{φ f} + C_{φ r}) \overset{\cdot}{φ} (4)$

式中:m为整车质量; m_s为车辆簧载质量; h_s为车辆簧载质量质心到侧倾轴的距离; $φ$ 为车辆侧倾角度; F_xij、F_yij分别为轮胎纵向力和侧向力, ij=fl、rl、fr、rr, 分别表示左前轮、左后轮、右前轮和右后轮; I_z为横摆转动惯量; I_xz为簧载质量转动惯量积; a、b分别为车辆质心到前、后轴的距离; d为车辆宽度; g为重力加速度; $K_{φ f} 、 K_{φ r}$ 分别为前、后轴侧倾刚度; $C_{φ f} 、 C_{φ r}$ 分别为前、后轴侧倾阻尼; v_x、v_y分别为车辆纵向速度和侧向速度; w_r为车辆横摆角速度; δ 为车辆前轮转向角度; I_x为车身的侧偏惯量。

以上公式中涉及的参数取值情况参考文献[23]中所述, 并建立GIM轮胎模型^[23], 综合考虑纵向力和横向力联合作用下模型力特性, 根据轮胎垂直载荷、侧偏角、轮速以及车轮滚动角速度可求得轮胎纵向力和侧向力。

2 车辆稳定性控制策略

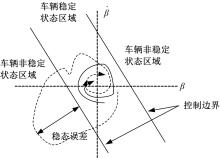
鉴于在失稳状态下, 车辆处于严重的非线性状态, 更适合用非线性理论进行研究, 所以可采用相平面法来研究质心侧偏角 $β$ 与车辆稳定性的联系^[8]。对于利用相平面来判断车辆的稳定状况, 文献[9, 10]做了详细探讨。

图1中所示的两条边界线所围成的区域则为车辆稳定状态区域, 两条边界线以外的区域则表示为车辆非稳定状态区域。

	Figure Option View Download New Window
	图1 β - $\overset{\cdot}{β}$ 相平面示意图Fig.1 β - $\overset{\cdot}{β}$ phase plane diagram

对本文中仿真车辆参数而言, 选取文献[9]中所述的 $β ⁃ \overset{\cdot}{β}$ 相平面稳定性区域系数B₁、B₂, 根据边界直线方程, 可以得出车辆稳定性判定准则:

$X_{region} = |2.41 \overset{\cdot}{β} + 9.615 β| \leq 1 (5)$

若式(5)成立, 表示车辆处于稳定状态; 当式(5)不成立时, 表示车辆已经处于失稳或临界失稳状态。

首先根据 $β ⁃ \overset{\cdot}{β}$ 相平面法则判定车辆的稳定性, 如果车辆处于非稳定状态, 那么启动稳定性控制模块, 直接进行稳定性控制; 倘若车辆处于稳定状态, 则启动操控性控制模块, 根据驾驶员对车辆加速度的要求和车辆横摆力矩的需求, 进行转矩分配, 优先利用电机的驱动/制动来实现横摆力矩分配; 当电机输出最大转矩仍然不能满足横摆力矩需求时, 启动液压制动系统来补偿, 具体过程如图2所示。

	Figure Option View Download New Window
	图2 车辆稳定性控制策略Fig.2 Vehicle stability control strategy

3 上层横摆力矩计算器

构建以横摆角速度和质心侧偏角为控制目标的汽车稳定性控制算法^[25]。根据横摆角速度、质心侧偏角与各自理想值的偏差, 利用滑膜控制设计稳定性控制器, 通过滑膜控制器计算出维持车辆稳定所需的上层横摆力矩。

采用参数容易调节且不需要精确建模的滑膜控制理论来设计稳定性控制器, 定义滑膜面S为^{[17, 18]}:

$\begin{array}{l} S = w_{r} - w_{rd} + fai (β - β_{d}) (6) \\ \overset{\cdot}{S} = {\overset{\cdot}{w}}_{r} - {\overset{\cdot}{w}}_{rd} + fai (\overset{\cdot}{β} - {\overset{\cdot}{β}}_{d}) (7) \end{array}$

式中:fai为系数; w_rd为理想横摆角速度; $β_{d}$ 为理想质的侧偏角。

由车辆横摆动力学模型公式^[6]得到:

$\begin{array}{l} I_{z} {\overset{\cdot}{w}}_{r} - I_{xz} \overset{\cdot \cdot}{φ} = a (F_{y fl} + F_{y fr}) \cos δ + \\ \frac{d}{2} (F_{y fl} - F_{y fr}) \sin δ - b (F_{y rl} + F_{y rr}) + \\ \frac{d}{2} (F_{x fr} - F_{x fl}) \cos δ + a (F_{x fl} + F_{x fl}) \sin δ + \\ \frac{d}{2} (F_{x rr} - F_{x rl}) (8) \end{array}$

由于 $δ$ 角度非常小, 本文中假定sinδ =0; 为了降低控制器的复杂程度, 由于 $\overset{\cdot \cdot}{φ}$ 变化率很小, 所以认为是0。因此, 可以将式(8)简化为如下形式:

$I_{z} {\overset{\cdot}{w}}_{r} = a (F_{y fl} + F_{y fr}) \cos δ - b (F_{y rl} + F_{y rr}) +$

$\frac{d}{2} (F_{x fr} - F_{x fl}) \cos δ + \frac{d}{2} (F_{x rr} - F_{x rl})$

令

$M_{z} = \frac{d}{2} (F_{x fr} - F_{x fl}) \cos δ + \frac{d}{2} (F_{x rr} - F_{x rl}) (9)$

式(9)是维持车辆稳定性需要施加的横摆力矩。由 $\overset{\cdot}{S} = 0,$ 可得:

$\begin{array}{l} \overset{\cdot}{S} = \frac{1}{I_{z}} (M_{z} + F_{y fl} a \cos δ + F_{y fr} a \cos δ - \\ F_{y rl} b - F_{y rr} b + I_{xz} \overset{\cdot \cdot}{φ}) - {\overset{\cdot}{w}}_{rd} + fai (\overset{\cdot}{β} - {\overset{\cdot}{β}}_{d}) = 0 (10) \\ M_{eq} = I_{z} [{\overset{\cdot}{w}}_{rd} - fai (\overset{\cdot}{β} - {\overset{\cdot}{β}}_{d})] - F_{y fl} a \cos δ - \\ F_{y fr} a \cos δ + F_{y rl} b + F_{y rr} b (11) \end{array}$

式中: $M_{eq}$ 为维持车辆稳定行驶所需的附加横摆力矩。

为了消除抖振问题, 用饱和函数代替符号函数, $M_{x}$ 为所需的保持车辆稳定行驶的横摆力矩。

$\{\begin{array}{l} M_{x} = M_{eq} + k sat (s / Δ) \\ sat = \{\begin{array}{l} x, |x| \leq 1 \\ sgn (x), |x| > 1 \end{array} \end{array} (12)$

式中: $Δ$ 为滑膜边界层厚度; k为系数; s为滑膜控制的求解。

如果按照传统的差动制动分配横摆力矩的方式, 会引起车辆速度的下降^[26], 且在有些工况下, 介入频繁, 导致轮胎力饱和, 更容易使车辆发生失稳。若轮胎力发生饱和, 车辆极容易发生侧滑导致失稳。为解决这样的问题, 本文基于各个轮胎利用率的情况, 利用二次规划理论, 设计横摆力矩分配器。

4 下层横摆力矩分配器

4.1 横摆力矩分配控制算法

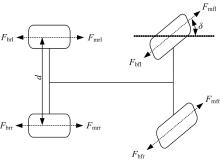
分析车辆受力情况如图3所示, 得到车辆所受的纵向力与总横摆力矩为:

$\{\begin{array}{l} F_{X} = F_{mfl} \cos δ + F_{mfr} \cos δ + F_{mrl} + F_{mrr} - \\ F_{bfl} \cos δ - F_{bfr} \cos δ - F_{brl} - F_{brr} \\ M_{Z} = \frac{d}{2} (- F_{mfl} \cos δ + F_{mfr} \cos δ - F_{mrl} + \\ F_{mrr} + F_{bfl} cosδ - F_{bfr} \cos δ + F_{brl} - F_{brr}) \end{array} (13)$

式中:F_m_i(i=fl, fr, rl, rr)为各个车轮的驱动力, 由各个轮毂电机提供; F_b_i(i=fl, fr, rl, rr)为各个车轮的制动力, 可由轮毂电机和液压制动系统分别或共同提供。

	Figure Option View Download New Window
	图3 车辆受力图示Fig.3 Vehicle force diagram

由于前轮转角较小, 可以认为 $\cos δ = 1,$ 将式(13)简化后, 变化成如下形式:

$\begin{array}{l} x_{c} = D u_{c} (14) \\ x_{c} = [F_{X} M_{Z}]^{T} (15) \\ u_{c} = [F_{mfl} F_{mfr} F_{mrl} F_{mrr} F_{bfl} F_{bfr} F_{brl} F_{brr}]^{T} (16) \\ D = [\begin{array}{l} 1 & 1 & 1 \\ - \frac{d}{2} & \frac{d}{2} & - \frac{d}{2} \end{array} \begin{array}{l} 1 & - 1 & - 1 \\ \frac{d}{2} & \frac{d}{2} & - \frac{d}{2} \end{array} \begin{array}{l} - 1 & - 1 \\ \frac{d}{2} & - \frac{d}{2} \end{array}] (17) \end{array}$

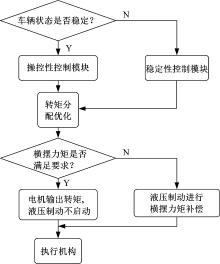
本文设定在电机输出范围内, 优先利用电机提供的制动/驱动力矩。若电机制动力矩不能满足横摆力矩要求, 则启动液压制动系统进行补偿。补偿量用总需求横摆力矩与电机所产生的横摆力矩的差值计算。

$\begin{array}{l} Δ M_{ZH} = Δ M_{Z} - Δ M_{ZM} = \\ (T_{mfr} - T_{mfl} + T_{mrr} - T_{mrl}) \frac{d}{2} (18) \end{array}$

式中: $Δ M_{ZM}$ 为电机力矩能够产生的横摆力矩; $Δ M_{ZH}$ 为液压制动能够产生的横摆力矩; $Δ M_{Z}$ 为总需求横摆力矩。

4.2 优化目标

以各个轮胎利用率之和最小为优化目标:

$\min J = \overset{4}{\sum_{i = 1}} \frac{F_{xi}^{2} + F_{yi}^{2}}{{(μ F_{zi})}^{2}} (19)$

其中: $μ$ 为路面附着系数; F_zi为各个车轮的垂直载荷, i=fl, fr, rl, rr。

由于轮胎附着椭圆表征了轮胎横、纵向力之间的关系, 因此, 可利用曲线拟合方式近似拟合出轮胎的附着椭圆曲线, 见图4。在一定侧偏角范围内, 轮胎横纵向力呈线性关系, 以此将轮胎横纵向力之间的关系线性化。

	Figure Option View Download New Window
	图4 轮胎附着椭圆示意图Fig.4 Tire attached to oval

轮胎附着椭圆曲线方程如下:

$\{\begin{array}{l} \frac{{F_{xi}}^{2}}{{l_{a}}^{2}} + \frac{{F_{yi}}^{2}}{{l_{b}}^{2}} = 1 \\ F_{xi} F_{yi} \geq 0 \end{array} (20)$

式中:l_a、l_b均为通过最小二乘法拟合椭圆曲线得到的数值, l_a> l_b> 0; i=fl, fr, rl, rr。

将优化目标函数改写为:

$\begin{array}{l} \min J = \overset{4}{\sum_{i = 1}} \frac{F_{xi}^{2} + {l_{b}}^{2} (1 - \frac{F_{xi}^{2}}{{l_{a}}^{2}})}{{(μ F_{zi})}^{2}} (21) \\ i = fl, fr, rl, rr \end{array}$

为减少算法复杂程度并方便计算, 忽略式(21)中 ${l_{b}}^{2}$ 这一项, 将其简化为:

$\begin{array}{l} \min J = \overset{4}{\sum_{i = 1}} \frac{(1 - \frac{{l_{b}}^{2}}{{l_{a}}^{2}}) F_{xi}^{2}}{{(μ F_{zi})}^{2}} (22) \\ i = fl, fr, rl, rr \end{array}$

故而将矩阵 $D$ 改写为如下形式:

$\begin{array}{l} D = [A B] (23) \\ A = [\begin{array}{l} 1 - \frac{{l_{b}}^{2}}{{l_{a}}^{2}} & 1 - \frac{{l_{b}}^{2}}{{l_{a}}^{2}} & 1 - \frac{{l_{b}}^{2}}{{l_{a}}^{2}} & 1 - \frac{{l_{b}}^{2}}{{l_{a}}^{2}} \\ - \frac{d}{2} & \frac{d}{2} & - \frac{d}{2} & \frac{d}{2} \end{array}] \\ B = [\begin{array}{l} - (1 - \frac{{l_{b}}^{2}}{{l_{a}}^{2}}) & - (1 - \frac{{l_{b}}^{2}}{{l_{a}}^{2}}) & - (1 - \frac{{l_{b}}^{2}}{{l_{a}}^{2}}) & - (1 - \frac{{l_{b}}^{2}}{{l_{a}}^{2}}) \\ \frac{d}{2} & - \frac{d}{2} & \frac{d}{2} & - \frac{d}{2} \end{array}] \end{array}$

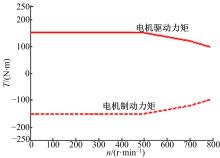
图5为轮毂电机外特性曲线。在考虑驾驶员对车辆纵向加速度需求后, 同时考虑轮胎纵向力不能超过地面附着极限的约束, 也不能超过制动器制动力和电机驱动力的极限。

	Figure Option View Download New Window
	图5 轮毂电机外特性曲线Fig.5 Motor external characteristic curve

4.3 约束条件

$\{\begin{array}{l} \min J = \overset{4}{\sum_{i = 1}} \frac{(1 - \frac{l_{b}^{2}}{l_{a}^{2}}) F_{xi}^{2}}{{(μ F_{zi})}^{2}}, i = fl, fr, rl, rr \\ s.t. \overset{4}{\sum_{i = 1}} F_{xi} = f (\tilde{a}) \\ Δ M_{Z} = [(F_{tfr} - F_{bfr}) - {(F}_{tfl} - F_{bfl})] \frac{d}{2} + \\ [(F_{trr} - F_{brr}) - {(F}_{trl} - F_{brl})] \frac{d}{2} \\ - μ F_{zi} \leq F_{t i} \leq \min (μ F_{zi}, \frac{T_{Mmax}}{r}) \\ - μ F_{zi} \leq F_{b i} \leq \min (μ F_{zi}, \frac{T_{bmax}}{r}) \end{array} (24)$

式中: $f (\tilde{a})$ 为驾驶员对速度控制意图与车轮受到纵向力之间的关系; $T_{Mmax}$ 为驱动电机输出最大转矩; $T_{bmax}$ 为液压制动系统输出的最大转矩。

4.4 二次规划优化分配算法

整理得到二次规划标准型为^[27]:

$\min J = u_{c}^{T} W u_{c} (25)$

将上述约束条件简化为:

$\{\begin{array}{l} D u_{c} = x_{c} \\ u_{cmin} \leq u_{c} \leq u_{cmax} \\ s . t . \overset{4}{\sum_{i = 1}} F_{xi} = f (\tilde{a}) \\ Δ M_{Z} = (F_{x fr} - F_{x fl}) \frac{d}{2} + (F_{x rr} - F_{x rl}) \frac{d}{2} \end{array} (26)$

电机驱动系统转矩响应延迟和液压制动系统的建压响应延迟, 通过引入一阶环节来表征该特性。

$\begin{array}{l} G (s) = \frac{1}{τ_{b} s + 1} (27) \\ G (s) = \frac{1}{τ_{m} s + 1} (28) \end{array}$

式中:τ _b为液压制动系统的增压响应延迟系数; τ _m为电机驱动系统的转矩响应延迟系数。

$\{\begin{array}{l} W = diag (\frac{\pm [1 - \frac{b^{2}}{a^{2}}]}{{(μ F_{zi})}^{2}}) \\ i = fl, fr, rl, rr, fl, fr, rl, rr \\ u_{c} = \arg \min_{u_{c \in Ω}} {(W_{u} u_{c})}_{2} \\ Ω = \arg \min_{u_{c}^{-} \leq u_{c} \leq u_{c}^{+}} {(W_{v} (D u_{c} - x_{c}))}_{2} \end{array} (29)$

式中: $W_{u}$ 为权重系数矩阵, 决定了各个车轮所分配纵向力之间的权重关系; $W_{v}$ 为分配需求权重矩阵, 决定了F_x与M_z之间的权重关系。

引入权重系数z, 当权重系数z足够大时, 以优先满足广义力约束, 在此基础上优化各执行器的控制输入。可将序列最小二乘法规划问题转化为加权最小二乘问题:

$\begin{array}{l} u_{c} = \arg \min_{u_{c}^{-} \leq u_{c} \leq u_{c}^{+}} ({(W_{u} u_{c})}_{_{2}}^{^{2}} + \\ z {(W_{u} (D u_{c} - x_{c}))}_{_{2}}^{^{2}}) (30) \end{array}$

经过二次规划得出的各个车轮驱动/制动力, 通过驱动/制动执行器作动到各个车轮上。

5 仿真验证

5.1 双移线试验

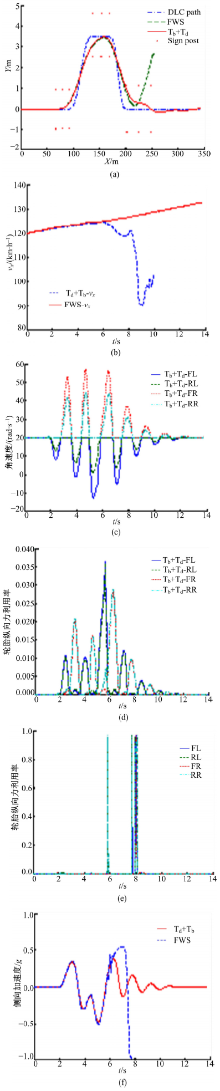
为了验证所提出的稳定性控制系统有效性, 以120 km/h进行闭环双移线试验, 道路附着系数为0.8, 且驾驶员无主动加速或者减速操作。仿真中, 加入基于差动制动的稳定性控制器作为对比^[26], 图6中“ DLC path” 为双移线轨迹, “ Sign post” 为试验标杆, 试验结果如图6(a)~(j)所示。

	Figure Option View Download New Window
	图6 双移线试验仿真结果Fig.6 Double lane change simulation test results

仿真中, 如图6(a)所示, 无控制的车辆(FWS)未能完成双移线试验, 基于差动制动的稳定性控制(T_b)和基于二次规划的稳定性控制(T_b+T_d)均完成双移线试验, 未发生撞杆或失稳。如图6(c)(d)(i)所示, “ T_b” 的横摆角速度响应较为理想, 侧向加速度响应在理想范围内, 质心侧偏角变化趋势也较为合理。但是“ T_b” 的车速下降程度比“ T_b+T_d” 大(见图6(b)), 原因是仅依靠制动力产生横摆力矩, 势必导致车速的下降, 产生同样大小的横摆力矩, 需要更大的制动力。这一点从车轮转矩也可以看出(见图6(g)(h)), “ 基于差动制动的稳定性控制” 消耗更多制动力矩去保持车辆稳定行驶。这也直接导致轮胎纵向力的利用率增加(见图6(e)(f)); 相反, 根据图6(h)所示, “ 基于二次规划的稳定性控制” 则依靠适当的驱动力/制动力产生同样大小的横摆力矩, 车速下降程度不大, 轮胎利用率也有所降低。

根据仿真试验的结果, 可得到如表1所示的3个评价指标结果。

表1 双移线试验评价结果 Table 1 Double-lane-change test evaluation results

需要说明的是, “ 轮胎纵向力利用率均值” 是根据式(21)取平均数计算得到; “ 单位时间各个车轮所受到的力矩均值” 为单位时间内取制动力矩与驱动力矩绝对值之和的平均数。

根据表1中结果可得, 相比于差动制动控制系统, 与理想车速的误差仅为0.96 km/h, 车速降低82.25%, 各个车轮受到平均力矩降低85.39%, 平均每个轮胎纵向力利用率下降 9.71%。

为了更准确评价仿真中两种稳定性控制器的综合性能, 根据文献[23]提出的车辆操控性评价指标(见表2), 结果表明, “ 基于差动制动的稳定性控制” 和“ 基于二次规划的稳定性控制” 的轨迹保持能力差别甚微, 后者略好; 侧向加速度方差表征发生翻车的可能性, 后者抵御翻车的能力更强; 转向时的忙碌程度, 前者更低, 这是因为差动制动降低了车速。侧向力系数总方差的对比, 后者具有一定优势, 表明了具有更高的侧向稳定裕度; 通过总体评价指标结果来看, “ 基于二次规划的稳定性控制器” 优势更明显, 综合性能更好。

表2 车辆操控稳定性评价结果 Table 2 Vehicle control stability evaluation results

5.2 加速试验

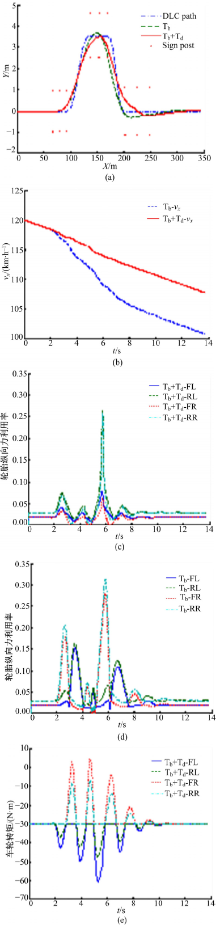
以120 km/h的初速度进行加速双移线试验, 仿真中始终为每个车轮施加20 N· m的驱动转矩, 模拟双移线中的加速超车工况。由于基于差动制动的稳定性控制器无法在车辆加速工况下工作, 因此加入FWS车辆进行对比。仿真结果如图7所示。

	Figure Option View Download New Window
	图7 加速试验仿真结果Fig.7 Simulation results of acceleration test

5.3 减速试验

以120 km/h的初速度进行减速双移线试验, 为各个车轮始终施加30 N· m的制动力矩, 模拟双移线中减速避障的工况。加入基于差动制动的稳定性控制器作为对比, 其结果如图8所示。

	Figure Option View Download New Window
	图8 减速试验仿真结果Fig.8 Simulation results of deceleration test

在加速试验中, FWS车辆直接发生失稳, 轮胎纵向力利用率在6 s和8 s左右达到100%(见图7(e)), 实际行驶路线严重偏离理想轨迹(见图7(a)), 未完成双移线试验; 搭载基于二次规划的稳定性控制的车辆平稳加速(见图7(b)), 通过分配车轮驱动/制动力矩(见图7(c)), 保证了车辆行驶稳定性, 并顺利完成双移线试验, 并且轮胎利用率始终保持在很小的范围内(见图7(d))。

在减速试验中, 搭载基于差动制动的稳定性控制器的车辆发生“ 撞杆” (见图8(a)), 未能完成试验; 而基于二次规划的稳定性控制器使车辆平稳减速(见图8(b)), 通过二次规划调整车轮驱动/制动力矩(见图8(e)), 使车辆顺利完成双移线试验; 相比于差动制动, 轮胎利用率降低很多(见图8(c)(d))。

6 结束语

本文结合滑膜控制理论与二次规划方法, 设计了分布式电动汽车稳定性控制系统。以轮毂电机与液压制动系统相结合的方式实现维持稳定行驶所需横摆力矩的分配。通过Matlab/Simulink进行闭环双移线仿真试验, 验证了二次规划控制策略的有效性。结果表明, 基于二次规划的分布式电动汽车的稳定性器能够保证车辆按照驾驶员意图行驶, 具有较好的鲁棒性。在提升了车辆操控稳定性和安全性的同时, 减小了对纵向车速的影响, 降低了轮胎利用率, 提高了车辆的稳定性裕度。相比于仅以差动制动形式的稳定性控制系统, 与理想车速的误差在1 km/h以内, 车速降低了82%, 各个车轮受到平均力矩降低了85.39%, 各个轮胎纵向力利用率均值下降了9.71%。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Nakazawa M, Isobe O, Takahashi S, et al. Braking force distribution control for improved vehicle dynamics and brake performance[J]. Vehicle System Dynamics, 1995, 24(4/5): 413-426. [本文引用:1]
[2]	He J, Crolla D A, Levesley M C, et al. Coordination of active steering, driveline, and braking for integrated vehicle dynamics control[J]. Journal of Automobile Engineering, 2006, 220(10): 1401-1420. [本文引用:2]
[3]	Li M, Jia Y, Matsuno F. Attenuating diagonal decoupling with robustness for velocity-varying 4WS vehicles[J]. Control Engineering Practice, 2016, 56: 49-59. [本文引用:2]
[4]	Tavasoli A, Naraghi M, Shakeri H. Optimized coordination of brakes and active steering for a 4WS passenger ca[J]. ISA Transactions, 2012, 51(5): 573-583. [本文引用:3]
[5]	Yin G, Wang S, Jin X. Optimal slip ratio based fuzzy control of acceleration slip regulation for four-wheel independent driving electric vehicles[J]. Mathematical Problems in Engineering, 2013(11) : 1-7. [本文引用:1]
[6]	Doumiati M, Sename O, Dugard L, et al. Integrated vehicle dynamics control via coordination of active front steering and rear braking[J]. European Journal of Control, 2013, 19(2): 121-143. [本文引用:2]
[7]	Mousavinejad E, Han Q L, Yang F, et al. Integrated control of ground vehicles dynamics via advanced terminal sliding mode control[J]. Vehicle System Dynamics, 2017, 55(2): 268-294. [本文引用:1]
[8]	Yim S, Kim S, Yun H. Coordinated control with electronic stability control and active front steering using the optimum yaw moment distribution under a lateral force constraint on the active front steering[J]. Journal of Automobile Engineering, 2016, 230(5): 581-592. [本文引用:2]
[9]	Hori Y. Future vehicle driven by electricity and control-research on four-wheel-motored" UOT Electric March II"[J]. IEEE Transactions on Industrial Electronics, 2004, 51(5): 954-962. [本文引用:2]
[10]	Lin C, Cheng X. A traction control strategy with an efficiency model in a distributed driving electric vehicle[J]. The Scientific World Journal, 2014, 2014: 261085. [本文引用:1]
[11]	Sakai S, Sado H, Hori Y. Motion control in an electric vehicle with four independently driven in-wheel motors[J]. IEEE/ASME Transactions on Mechatronics, 1999, 4(1): 9-16. [本文引用:1]
[12]	Geng C, Mostefai L, Denaï M, et al. Direct yaw-moment control of an in-wheel-motored electric vehicle based on body slip angle fuzzy observe[J]. IEEE Transactions on Industrial Electronics, 2009, 56(5): 1411-1419. [本文引用:1]
[13]	Chen Y, Wang J. Design and evaluation on electric differentials for overactuated electric ground vehicles with four independent in-wheel motors[J]. IEEE Transactions on Vehicular Technology, 2012, 61(4): 1534-1542. [本文引用:1]
[14]	Liu H, Chen X, Wang X. Overview and prospects on distributed drive electric vehicles and its energy saving strategy[J]. Prz Elektrotech, 2012, 88: 122-125. [本文引用:1]
[15]	张金柱, 张洪田, 孙远涛. 电动汽车稳定性的横摆力矩控制[J]. 电机与控制学报, 2012, 16(6): 75-80. Zhang Jin-zhu, Zhang Hong-tian, Sun Yuan-tao. The direct yaw control of electric vehicle stability control[J]. Electric Machines and Control, 2012, 16(6): 75-80. [本文引用:1]
[16]	石志潇. 电动汽车电液复合制动系统转弯稳定性控制研究[D]. 南京: 南京航空航天大学能源与动力学院, 2015. Shi Zhi-xiao. Research on cornering stability control of electric vehicle based on electric-hydraulic brake system[D]. Nanjing: College of Energy and Power Engineering, Nanjing University of Aeronautics and Astronautics, 2015. [本文引用:1]
[17]	绳辰. 轮毂电机驱动电动汽车纵向稳定性控制研究[D]. 北京: 北京交通大学机械与电子控制工程学院, 2014. Sheng Chen. Study on longitudinal stability of in-wheel motor vehicle[D]. Beijing: School of Mechanical, Electronic and Control Engineering, Beijing Jiaotong University, 2014. [本文引用:2]
[18]	滕冬冬. 轮毂电机电动汽车再生制动与稳定性控制研究[D]. 合肥: 合肥工业大学汽车与交通工程学院, 2016. Teng Dong-dong. Study on regenerative braking and stability control for in-wheel motor driven electric vehicle [D]. Hefei: School of Machinery and Automobile Engineering, Hefei University of Technology, 2016. [本文引用:2]
[19]	Amodeo M, Ferrara A, Terzaghi R, et al. Wheel slip control via second-order sliding-mode generation[J]. IEEE Transactions on Intelligent Transportation Systems, 2010, 11(1): 122-131. [本文引用:1]
[20]	Cho K, Kim J, Choi S. The integrated vehicle longitudinal control system for ABS and TCS[C]∥Control Applications (CCA), IEEE, 2012: 1322-1327. [本文引用:1]
[21]	Tanelli M, Ferrara A. Wheel slip control of road vehicles via switched second order sliding modes[J]. International Journal of Vehicle Design, 2013, 62(2-4): 231-253. [本文引用:1]
[22]	Drakunov S, Ozguner U, Dix P, et al. ABS control using optimum search via sliding modes[J]. IEEE Transactions on Control Systems Technology, 1995, 3(1): 79-85. [本文引用:1]
[23]	高琳琳, 金立生, 郑义, 等. 四轮转向车辆的径向基函数神经网络复合控制器设计[J]. 吉林大学学报: 工学版, 2016, 46(2): 366-372. Gao Lin-lin, Jin Li-sheng, Zheng Yi, et al. Design of radial basis function neural network compound controller for four wheel steering vehicle[J]. Journal of Jilin University(Engineering and Technology Edition), 2016, 46(2): 366-372. [本文引用:4]
[24]	魏朗. 用于碰撞事故中车辆动力学模拟的轮胎模型分析[J]. 西安公路交通大学学报, 1999(2): 73-76. Wei Lang. An analysis of vehicle dynamic simulating tire model used in collisions accidents[J]. Journal of Xi'an Highway University, 1999(2): 73-76. [本文引用:1]
[25]	杜峰. 基于线控技术的四轮主动转向汽车控制策略仿真研究 [D]. 西安: 长安大学汽车学院, 2009. Du Feng. Simulation research on control strategies for active 4WS vehicle based on the steer-by-wire technology [D]. Xi'an: School of Automobile, Chang'an University, 2009. [本文引用:1]
[26]	Jin L, Xie X, Shen C, et al. Study on electronic stability program control strategy based on the fuzzy logical and genetic optimization method[J]. Advances in Mechanical Engineering, 2017, 9(5): 1687814017699351. [本文引用:2]
[27]	Petersen J A M, Bodson M. Constrained quadratic programming techniques for control allocation[J]. IEEE Transactions on Control Systems Technology, 2006, 14(1): 91-98. [本文引用:1]

1995

0.0

... 0 引言汽车稳定性控制系统是当前国际上汽车安全领域的研究热点^[1] ...

2006

0.0