基于微分器的直驱电液伺服系统离散滑模控制

引用本文

姜继海, 葛泽华, 杨晨, 梁海健. 基于微分器的直驱电液伺服系统离散滑模控制[J].吉林大学学报（工学版）, 2018,48(5): 1492-1499
JIANG Ji-hai, GE Ze-hua, YANG Chen, LIANG Hai-jian. Differentiator-based discrete variable structure controller for direct drive electro-hydraulic servo system[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1492-1499 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170584
Permissions

基于微分器的直驱电液伺服系统离散滑模控制

姜继海¹, 葛泽华¹, 杨晨², 梁海健¹

1.哈尔滨工业大学机电工程学院,哈尔滨 150080

2.中国航发控制系统研究所,江苏无锡 214063

作者简介:姜继海(1957-),男,教授,博士生导师.研究方向:流体传动与控制.E-mail:jjhlxw@hit.edu.cn

基金:国防基础科研基金项目(A2320060114);哈尔滨市科技创新人才研究专项基金项目(2010B090400548)

摘要

直驱式容积控制电液伺服系统具有结构紧凑、效率高等优点,但该系统也存在着死区和非线性特征。为了解决该问题,本文建立了直驱式容积控制电液伺服系统的状态方程并对其进行了离散化。采用三阶积分链式微分器,通过对活塞杆位移的信号进行微分,实时得到活塞杆的速度和加速度信号,构成系统的全状态反馈。采用基于趋近率的离散滑模控制算法设计控制器并进行仿真和实验研究,结果表明,该控制器的位置跟踪特性明显优于PID控制器,能够提高直驱式容积控制电液伺服系统的控制性能。

关键词: 流体传动与控制; 直驱式容积控制; 离散滑模控制; 微分器

中图分类号:TP273.4 文献标志码:A 文章编号:1671-5497(2018)05-1492-08

Differentiator-based discrete variable structure controller for direct drive electro-hydraulic servo system

JIANG Ji-hai¹, GE Ze-hua¹, YANG Chen², LIANG Hai-jian¹

1.School of Mechatronics Engineering, Harbin Institute of Technology, Harbin 150080,China

2.AECC Aero Engine Control System Institute, Wuxi 214063, China

Abstract

Direct Drive Volume Control (DDVC) servo system is a novel hydraulic servo system. With the continuous development of motor servo technology, it has been widely used in industrial and aerospace applications. The system has advantages of compact structure and high efficiency, but also has defects in dead zone and non-linear characteristics. In order to solve these problems, the state equation of the system was established and discretized. By using the third-order integral chain differentiator, the real-time values of the rod velocity and acceleration were obtained from the measurement signal of displacement, which constitute the full state feed-back control system. A nonlinear controller was designed with the Discrete Variable Structure Control (DVSC) algorithm based on the approach law. The simulation and experimental results show that the DVSC controller has better position tracing characteristics than traditional PID controller, which improves the controlling performance of DDVC servo system.

Keyword: hydraulic transmission and control; direct drive volume control; discrete variable structure control; differentiator

文章图片

0 引言

直驱式容积控制电液伺服系统(Direct drive volume control, DDVC)是一种新型液压伺服系统, 随着电机伺服技术不断发展, 它得到了越来越广泛的应用^{[1, 2, 3]}。DDVC系统充分发挥伺服电动机的特性, 采用调节电动机旋转方向和转速的方法来控制压力油的输出方向和流量大小^[4]。由于该系统中没有节流元件, 因此压力损失少、效率高, 节能效果显著。同时由于其可靠性高、结构紧凑等特点, 在注塑机、火箭与舰船舵机、风力发电机、飞机作动器、机器人关节等方面有着广泛的应用^{[5, 6, 7, 8, 9, 10]}。

DDVC系统在执行机构的运动过程中具有液压系统典型的非线性特征; 且系统中部分参数如油液弹性模量等难以求取, 具有参数不确定性, 因此要求控制系统对模型误差不敏感。同时, 由于在电机换向时, 液控单向阀有一定的滞后导致无法及时补油, 且泵在低速旋转时输出流量不足以补偿系统的泄漏, 会有工作死区产生。上述特性会严重影响直驱式电液伺服系统性能, 传统的PID控制不能够补偿系统中存在的死区和非线性, 使得其跟踪精度很难提高, 因此有必要提出一种新的控制策略对其加以改善。滑模变结构控制是一种根据系统当前的状态, 在动态过程中不断改变控制器参数, 使系统按照预定规律运动的控制方法^[11]。相关研究成果表明, 该控制方法能够较好的抑制液压系统的死区和非线性等问题, 且受参数误差的影响较低^{[12, 13, 14]}。针对计算机控制的离散时间系统, 有学者提出离散滑模控制(Discrete variable structure control, DVSC)算法并获得广泛应用^{[15, 16, 17, 18]}。在本研究中, 采用DVSC控制器来降低DDVC系统死区和非线性的影响。

1 DDVC系统的数学模型

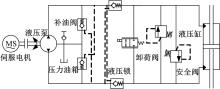
本文用于实现离散滑模控制的DDVC系统如图1所示。

	Figure Option View Download New Window
	图1 DDVC系统原理图Fig.1 Block diagram of DDVC system

该系统采用伺服电机驱动双旋向定量泵为液压缸提供压力油, 通过调节伺服电机的转速来控制活塞杆的运动速度。采用密闭压力油罐通过液控单向阀对系统进行补油。为保证系统安全, 采用液压锁防止液压缸受外负载作用力而动作, 用一组安全阀来限制系统最大压力, 并通过电磁换向阀实现系统卸荷。

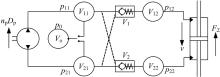
为了建立DDVC液压系统的非线性数学模型, 将系统中各元件间的管道容积分为5个部分, 如图2所示。

	Figure Option View Download New Window
	图2 DDVC系统容腔分布示意图Fig.2 Volume distribution of DDVC system

图2中的V₀为系统增压油箱容积, 压力设为p₀; V₁₁和V₂₁为液控单向阀与液压泵之间的容积, 在系统动作时体积不变, 压力设为p₁₁、p₁₂; V₁₂和V₂₂为液控单向阀与液压缸之间的管路容积, 在活塞杆运动过程中大小不断改变, 压力设为p₂₁、 ${p_{22}}^{[19]}$ 。以向下为活塞杆运动的正方向, 建立液压缸正、反向运动时的DDVC系统泵控液压缸机构的流量连续性方程:

$\begin{array}{l} n_{p} D_{p} = A \overset{\cdot}{x} + \frac{V_{11} + V_{12} + Ax}{β_{e}} {\overset{\cdot}{p}}_{12} + \\ C_{t} Δp, 正向运动 (1) \\ n_{p} D_{p} = A \overset{\cdot}{x} + \frac{V_{21} + V_{22} + A (L - x)}{β_{e}} {\overset{\cdot}{p}}_{22} + \\ \frac{V_{12} + Ax}{β_{e}} {\overset{\cdot}{p}}_{12} + C_{t} Δp, 反向运动 (2) \end{array}$

式中:n_p为液压泵转速, rad/s; D_p为液压泵排量, m³/rad; x为液压缸活塞杆位移, m; A为液压缸活塞有效作用面积, m²; L为液压缸活塞杆运动长度, m; β _e为液压油体积弹性模量, Pa; C_t为液压系统泄漏系数, m³/(Pa· s)。

建立液压缸在外力作用下的力平衡方程:

$A (p_{12} - p_{22}) = F_{Σ} = M \overset{\cdot \cdot}{x} + B_{c} \overset{\cdot}{x} + Kx + F_{L} (3)$

式中:M为液压缸运动部分质量, kg; B_c为黏性阻尼系数, N· s/m; K为负载弹簧刚度, N/m; F_L为液压缸负载力, N。

以活塞杆的位移、速度和加速度作为状态变量, 建立活塞杆运动的状态方程:

$\begin{array}{l} \overset{\cdot}{X} = [\begin{array}{l} {\overset{\cdot}{x}}_{1} \\ {\overset{\cdot}{x}}_{2} \\ {\overset{\cdot}{x}}_{3} \end{array}] = [\begin{array}{l} \overset{\cdot}{x} \\ \overset{\cdot \cdot}{x} \\ \overset{\dots}{x} \end{array}] = \\ [\begin{array}{l} 0 & 1 & 0 \\ 0 & 0 & 1 \\ a_{31} & a_{32} & a_{33} \end{array}] [\begin{array}{l} x_{1} \\ x_{2} \\ x_{3} \end{array}] + [\begin{array}{l} 0 \\ 0 \\ b \end{array}] u + [\begin{array}{l} 0 \\ 0 \\ f_{3} (x, t) \end{array}] (4) \end{array}$

式中:

$\begin{array}{l} a_{31} = - \frac{β_{e} C_{t} K}{MV}; \\ a_{32} = - \frac{β_{e}}{MV} (A^{2} + \frac{VK}{β_{e}} + B_{c} C_{t}); \\ a_{33} = - \frac{B_{c}}{M} - \frac{β_{e} C_{t}}{V}; \\ f_{3} (x, t) = \frac{1}{M} {\overset{\cdot}{F}}_{L} + \frac{β_{e} C_{t}}{MV} F_{L} + g (x, t); \\ b = \frac{β_{e} A D_{p} K_{sp}}{MV}; \\ V = \{\begin{array}{l} V_{1}, 正向 \\ V_{2}, 反向 \end{array} 。 \\ V_{1} = V_{11} + V_{12} + Ax; \\ V_{2} = \frac{1}{λ_{ratio} - 1} [λ_{ratio} V_{12} + V_{21} + V_{22} + (λ_{ratio} - 1) Ax + AL] 。 \end{array}$

$g (x, t)$ 为负载干扰不确定项, $λ_{ratio}$ 为液控单向阀控制比。

由于液压系统中的部分参数如油液的弹性模量、泄漏系数等在实验条件下无法精确测量, 且会随着系统结构状态等不断发生改变。在系统工作过程中, 又不可避免得存在着一定的外部干扰, 因此需要建立包含误差项和外部扰动存在条件下的系统状态方程:

$\overset{\cdot}{X} (t) = (A + Δ A) X (t) + (B + Δ B) u (t) + f (t) (5)$

式中: $A$ 为变换矩阵, A∈ R^{3× 3}; B为初值系数, B∈ R^{3× 3}; Δ A、Δ B为系统误差, Δ A, Δ B∈ R^{3× 3}; u(t)为系统初值, u∈ R; f(t)为系统干扰, f∈ R^{3× 1}。

2 离散滑模控制器设计

2.1 微分器设计

由前述分析知, 需要获取DDVC系统的位置、速度和加速度的反馈信号以实现全闭环反馈。在本研究中, 速度和加速度信号需要通过对位置信号求导来获得。但是由于通过传感器采集到的位置信号存在着一定的噪声和扰动, 用传统差分的方式求取信号导数会导致误差放大, 因此设计能削弱噪声和干扰影响的三阶积分链式微分器, 用来估计活塞杆的速度和加速度^[20]:

$\{\begin{array}{l} {\overset{\cdot}{\hat{x}}}_{1} (t) = {\hat{x}}_{2} (t) \\ {\overset{\cdot}{\hat{x}}}_{2} (t) = {\hat{x}}_{3} (t) \\ {\overset{\cdot}{\hat{x}}}_{3} (t) = - \frac{1}{ε_{d}^{3}} {a_{1} [{\hat{x}}_{1} (t) - y (t)] + \\ a_{2} ε_{d} {\hat{x}}_{2} (t) + a_{2} ε_{d}^{2} {\hat{x}}_{3} (t)} \end{array} (6)$

式中: ${\hat{x}}_{i} (t) 为 x_{i} (t)$ 状态向量的估计值; ε _d为微分器放大系数; a_i为常数, 取a₁= r³、a₂= 3r²、a₃= 3r, 以使系统特征多项式稳定; y(t)为活塞杆位移。

当ε _d取值较小时, 有 $x_{i} (t) \to y^{(i - 1)} (t)$ 成立^[21]。

对微分器参数进行线性化, 得出位置参数的取值 ${\hat{x}}_{1}$ 与采集值y之间的传递函数:

$\begin{array}{l} \frac{{\hat{X}}_{1}}{Y} = \frac{a_{1}}{{ε_{d}}^{3} s^{3} + {ε_{d}}^{2} a_{3} s^{2} + ε_{d} a_{2} s + a_{1}} = \\ \frac{R^{3}}{{(s + R)}^{3}} (7) \end{array}$

式中:R=l/ε _d。取ε _d=0.01, l= 1.5, 则R=150。

为了避免差分法对微分器的计算精度产生影响, 通过四阶Runge-Kutta法将状态方程式(6)离散化, 得到 ${\hat{x}}_{i} (t)$ 的表达式:

$\begin{array}{l} {\hat{x}}_{i} (k) = {\hat{x}}_{1} (k - 1) + \frac{T_{s}}{6} (K_{i 1} + 2 K_{i 2} + 2 K_{i 3} + K_{i 4}) (8) \\ 其中 : \\ \begin{array}{l} K_{i 1} = {\hat{f}}_{1} (\hat{X} (k - 1), {\hat{x}}_{i - 1} (k), \dots, {\hat{x}}_{1} (k), t) \\ K_{i 2} = K_{i 1} + 0.5 T_{s} K_{i 1} \\ K_{i 3} = K_{i 1} + 0.5 T_{s} K_{i 2} \\ K_{i 4} = K_{i 1} + T_{s} K_{i 3} \end{array} \end{array}$

式中: $K_{i 1} = {\hat{f}}_{1} (\hat{X} (k - 1), {\hat{x}}_{i - 1} (k), \dots, {\hat{x}}_{1} (k), t)$

2.2 控制器设计

使用零阶保持法离散化活塞杆的运动方程(5), 以T_s为时间采样周期:

$\begin{array}{l} X (k + 1) = (A_{d} + Δ A_{d}) X (k) + \\ (B_{d} + Δ B_{d}) u (k) + f_{d} (k) (9) \end{array}$

式中: $A_{d} 为状态变换矩阵, A_{d} = {L^{- 1} [{(sI - A)}^{- 1}]|}_{t = T_{s}}; B_{d}$ 为控制输入矩阵, B_d= $\int_{0}^{T_{s}}$ L^-1 $[{(sI - A)}^{- 1}]$ · Bdt; f_d为系统扰动和外负载, f_d(k)=f(kT_s)· $\int_{0}^{T_{s}}$ L^-1 $[{(sI - A)}^{- 1}]$ dt。

设活塞杆的位置指令信号为 $X_{d} (k) \in R^{n},$ n为状态方程阶数, 则系统偏差 $E (k) = X_{d} (k) - X (k) 。$

离散滑模控制为准滑模控制, 在滑模控制器中取切换函数 $s (k) = C \cdot E (k),$ 设计切换带:

$S_{Δ} = \{x \in R^{n} | - Δ < s (k) = C \cdot E (k) < Δ\} (10)$

式中:向量 $C$ 为超平面参数阵, $C = [c_{1}, c_{2}, \dots, c_{n - 1}, 1] 。$

设DDVC系统符合参数变化和外来扰动的不变性条件, 即有 $1 \times n 矩阵 \tilde{A}$ 和系数 $\tilde{B}$ 和 $\tilde{d}$ 使下式成立

$Δ A_{d} = B_{d} {\tilde{A}}_{d}, Δ B_{d} = B_{d} {\tilde{B}}_{d}, f_{d} (k) = B_{d} {\tilde{f}}_{d} (k) (11)$

将式(11)带入式(9)中, 得到:

$\begin{array}{l} X (k + 1) = A_{d} X (k) + B_{d} [(1 + {\tilde{B}}_{d}) u + \\ {\tilde{A}}_{d} X + {\tilde{f}}_{d} (k)] (12) \end{array}$

可以应用在DVSC算法中的趋近律为^[18]:

$\begin{array}{l} s (k + 1) = (1 - q T_{s}) s (k) - ε T_{s} sgn (s (k)) \\ ε > 0, q > 0 (13) \end{array}$

式中:参数q为收敛速度系数, 影响各状态变量从任意初值向滑模面运动的快慢; 参数 $ε$ 为高频切换增益, 影响着滑模面对系统状态变量的束缚强度。二者取值过大会导致运动产生过大的超调或抖振。滑模控制器切换带的宽度为 $2 Δ = \frac{2 ε T_{s}}{1 - q T_{s}} 。$

由于微分器的带宽设计较高, 可以认为 $\hat{s} (k) = C \cdot X_{d} (k) - C \cdot \hat{X} (k) \approx s (k)$ 成立。控制器的等效输入量u_eq(k)满足:

$u_{eq} (k) = (1 + {\tilde{B}}_{d}) u (k) + {\tilde{A}}_{d} \hat{X} (k) + \tilde{f} (k) (14)$

将式(12)代入到式(14)中, 得出DVSC控制率表达式:

$\begin{array}{l} u_{eq} (k) = - (C B_{d})^{- 1} [C A_{d} X_{d} (k + 1) - C A_{d} \hat{X} (k) - \\ (1 - q T_{s}) s (k) - ε T_{s} sgn (s (k))] (15) \end{array}$

3 DVSC控制器的仿真分析

3.1 DVSC控制器参数求取

对于文中系统的DVSC控制器, 收敛速度系数q和高频切换增益ε 可以在实验过程中根据需求直接进行取值。为了设计滑模切换函数, 需要对超平面参数阵 $C$ 进行求取。

将DDVC系统状态方程表达为:

$\{\begin{array}{l} {\overset{\cdot}{X}}_{11} = A_{11} X_{11} + A_{12} X_{12} \\ {\overset{\cdot}{X}}_{12} = A_{21} X_{12} + A_{22} X_{22} + bu \\ s = C_{1} (X_{11 d} - X_{11}) + C_{2} (X_{12 d} - X_{12}) \end{array} (16)$

式中: $[X_{11 d}] = {[x_{1 d}, x_{2 d}]}^{T}; [X_{11 d}] = {[x_{1 d}, x_{2 d}]}^{T}; [X_{12 d}] = [x_{3 d}]; [X_{12 d}] = [x_{3 d}]; C_{1} = {[c_{1}, c_{2}]}^{T};$ 取 $C_{2} = [1] 。$

根据文献[22], 根据现代控制理论状态反馈的原理, 采用基于极点配置概念设计DDVC系统的超平面参数阵 $C 。$

取X_d(t) = 0, 则滑模切换函数为:

$s = - C_{1} X_{11} - C_{2} X_{12} = 0 (17)$

将式(16)做线性变换:

$\{\begin{array}{l} {\overset{\cdot}{X}}_{11} = (A_{11} - A_{12} C_{1}) X_{11} \\ {\overset{\cdot}{X}}_{12} = - C_{1} (A_{11} - A_{12} C_{1}) X_{11} \end{array} (18)$

由于本研究中对象系统是能控的, 所以其子系统(A₁₁, A₁₂)能控。设λ ₁和λ ₂为子系统(A₁₁, A₁₂)的理想极点, 列出以λ ₁和λ ₂为零点的特征多项式:

$σ (z) = \overset{3}{\prod_{i = 1}} (s_{1} - λ_{i}) = |s_{1} I - A_{11} + A_{12} \cdot C_{1}| (19)$

则超平面参数阵 $C$ 的表达形式为:

$C = [λ_{1} λ_{2}, λ_{1} + λ_{2}, 1] (20)$

为了尽量避免超调且方便设计计算, 取λ ₁=λ ₂=1000。

3.2 DDVC系统仿真分析

对采用DVSC控制器的直驱式容积控制系统进行仿真, 使其分别跟踪位置阶跃信号和正弦信号, 检验位置跟踪精度以及系统快速性。通过对多组DVSC控制器参数q和ε 的取值进行仿真和实验, 得q = 100和ε =180为其中控制效果较好的取值。PID控制器的参数较优的取值为k_p=51.188、k_i=17.268、k_d=0.763。对于两种控制器, 取用能够使控制快速性和跟踪精度较优的取值进行仿真与实验对比, 具有一定的代表性。在仿真过程中, 系统参数通过理论计算和实验求取, 取值精度可以满足控制系统的要求, 仿真模型的精确性也通过实验得到了验证。系统参数如表1所示^[19]。

表1 DDVC系统参数表 Table 1 Parameters of DDVC system

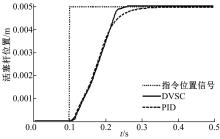
(1)阶跃信号响应

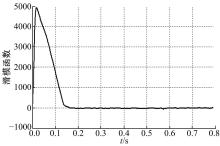
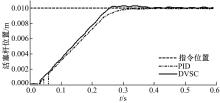
在0.005 m的位置阶跃信号指令下, 得到其响应仿真结果(见图3)。可以看出由于电机最大转速的限制, DVSC和PID控制器下系统的响应基本一致。在接近指令位置时, DVSC控制器下的活塞杆的运动速度仍然较快, 而PID控制器下活塞杆速度则开始降低, 因此DVSC控制器的调节时间略小于PID控制器, 二者均未产生超调。由图4中滑模函数s的变化情况可知, 在活塞杆位置即将达到预定位置时, DVSC控制器能够快速完成由趋近模态向准滑动模态的转换, 系统的抖振也很小。

	Figure Option View Download New Window
	图3 阶跃响应仿真曲线Fig.3 Simulation result of step response

	Figure Option View Download New Window
	图4 滑模函数s值变化曲线Fig.4 Evolution of s in DVSC controller

(2)正弦跟踪响应

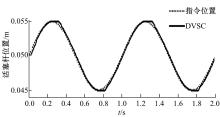
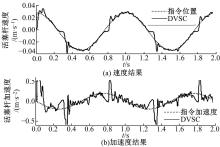
在0.005 m幅值, 1 Hz频率的位置正弦信号输入下, 获得其响应的仿真结果(见图5)。可以看出在DVSC控制器作用下, 活塞杆能够较好得实现对1Hz正弦位置信号的跟踪, 且该仿真能够模拟出电机换向时产生的系统死区。图6为微分器求取的速度和加速度结果, 说明该微分器能够较好得完成速度和加速度监测任务。

	Figure Option View Download New Window
	图5 正弦响应仿真曲线Fig.5 Simulation result of sinusoidal response

	Figure Option View Download New Window
	图6 速度和加速度估计仿真结果Fig.6 Simulation of speed and acceleration estimation

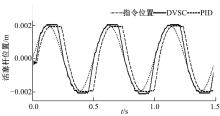
在0.002 m幅值, 2 Hz频率的位置正弦信号输入下, 获得其相应的仿真结果(见图7)。可以看出在2 Hz正弦输入信号的条件下, DVSC控制能够发挥出自己的优势, 跟踪响应曲线的幅值与相位差值都明显小于PID控制, 且能更好地抑制系统死区。

	Figure Option View Download New Window
	图7 2 Hz正弦响应仿真曲线对比Fig.7 Simulation results of 2 Hz sinusoidal response

4 DVSC控制器的实验验证

利用DDVC实验装置对离散滑模控制器进行实验研究, 实验台如图8所示。实验原理与图1基本相同, 采用单出杆双作用对称液压缸代替图中双出杆对称液压缸, 使实验台结构更加紧凑。系统的实验参数与仿真参数相同。实验过程中, 通过计算机控制软件向单片机发送控制指令。单片机同时获取指令信号和检测信号, 经过计算后输出电机伺服驱动器的控制指令, 控制液压系统动作。系统的活塞杆位置信号通过内置于液压缸中的位移传感器进行采集。

	Figure Option View Download New Window
	图8 DDVC系统实验装置Fig.8 DDVC system test rig

在0.005 m位置阶跃信号输入下, 获得其响应实验结果(见图9)。通过比较DVSC控制器与PID控制器下的阶跃响应曲线可以发现, 两者的稳态精度基本相同, 而前者的调节时间则略小于后者, 与仿真结果相符。

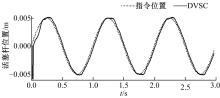
	Figure Option View Download New Window
	图9 阶跃响应实验曲线Fig.9 Experimental results of step response

在0.005 m幅值, 1 Hz频率的位置正弦信号输入下, 获得其响应实验结果(见图10)。该曲线的滞后较小, 在换向时存在着一定的死区, 与仿真结果基本相同。图11为微分器计算的活塞杆速度和加速度结果, 实验结果与仿真结果基本相同, 但由于齿轮泵的流量脉动引起曲线抖动更加剧烈。

	Figure Option View Download New Window
	图10 正弦响应实验曲线Fig.10 Experimental results of sinusoidal response

	Figure Option View Download New Window
	图11 速度和加速度估计实验结果Fig.11 Experiment of speed and acceleration estimation

在0.002 m幅值, 2 Hz频率的位置正弦信号输入下, 获得其响应实验结果(见图12)。可以看出该实验曲线与仿真结果基本一致, PID控制下执行器位置的相位滞后平均为5.4%, 而DVSC控制下执行器位置的相位滞后平均为2.6%, 其相位滞后减小了51.9%; PID控制下执行器位置的跟踪误差平均为0.490 mm, 而DVSC控制下执行器位置的跟踪误差平均为0.307 mm, 其跟踪误差减小了37.3%。可见DVSC控制的跟踪响应速度和跟踪精度明显优于PID控制, 在活塞杆改变运动方向时, DVSC控制器能够使系统迅速脱离死区, 对死区和非线性的抑制作用更强。

	Figure Option View Download New Window
	图12 2 Hz正弦响应实验曲线对比Fig.12 Experimental results of 2 Hz sinusoidal response

5 结束语

本文以DDVC电液伺服系统为研究对象, 考虑系统管道容积变化对参数的影响, 将基于趋近律的DVSC算法应用于DDVC电液伺服系统中, 提高了系统的跟踪性能。为实际控制系统设计三阶积分链式微分器, 获得离散滑模控制算法所需要的全部状态:液压缸位移、速度、加速度。仿真验证表明, 所设计的微分器能够满足要求, 可提供较为精确的状态估计。基于所估计的状态, 采用指数趋近律, 设计了离散滑模控制器。仿真和实验结果都表明, 基于趋近律的离散滑模控制器对DDVC电液伺服系统死区和非线性具有更强的抑制作用, 跟踪滞后和稳态误差较小, 显著优于传统的PID控制策略。该控制方法可以进一步提升DDVC电液伺服系统的工程应用场景。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	刘庆和. 直接驱动容积控制电液传动系统[J]. 机床与液压, 2009(11): 233-238. Liu Qing-he. Direct drive volume control electro-hydraulic system[J]. Machine Tool and Hydraulics, 2009(11): 233-238. [本文引用:1]
[2]	姜继海, 刘乔, 侯珍秀. 直驱式转叶舵机的特点及关键技术[J]. 液压与气动, 2014(9): 1-11. Jiang Ji-hai, Liu Qiao, Hou Zhen-xiu. The advantages and key technologies of direct drive volume rotary vane steering gear[J]. Chinese Hydraulics and Pneumatics, 2014(9): 1-11. [本文引用:1]
[3]	刘军龙, 姜继海, 卢天日, 等. 直驱式电液伺服主动质量驱动系统[J]. 哈尔滨工业大学学报, 2011, 43(9): 51-55. Liu Jun-long, Jiang Ji-hai, Lu Tian-ri, et al. Direct drive volume control electro-hydraulic servo active mass driver system. [J] Journal of Harbin Institute of Technology, 2011, 43(9): 51-55. [本文引用:1]
[4]	姜继海, 涂婉丽, 曹健. 直驱式容积控制电液伺服系统动态性能研究[J]. 液压与气动, 2005 (8): 29-32. Jiang Ji-hai, Tu Wan-li, Cao Jian. Research on dynamic performance of direct volume control electro-hydraulic servo system[J]. Chinese Hydraulics and Pneumatics, 2005(8): 29-32. [本文引用:1]
[5]	许宏光, 曹健, 赵阳. 直驱式电液伺服系统及其在注塑机上的应用[J]. 机床与液压, 2005(3): 119-120, 90. Xu Hong-guang, Cao Jian, Zhao Yang. Direct drive electro-hydraulic servo system and its application in plastic injection machine[J]. Machine Tool and hydraulics, 2005(3): 119-120, 90. [本文引用:1]
[6]	姜继海, 赵进宝, 刘乔, 等. 火箭舵机转速排量复合控制电动静液作动系统设计与仿真[J]. 液压与气动, 2015(1): 11-16. Jiang Ji-hai, Zhao Jin-bao, Liu Qiao, et al. Design and simulation of electro-hydrostatic actuation system controlled by variable pump and variable motor composite for rocket rudde[J]. Chinese Hydraulics and Pneumatics, 2015(1): 11-16. [本文引用:1]
[7]	苏文海, 姜继海, 王晓晶, 等. 直驱式电液伺服转叶舵机定量反馈理论鲁棒控制[J]. 吉林大学学报: 工学版, 2011, 41(3): 670-675. Su Wen-hai, Jiang Ji-hai, Wang Xiao-jing, et al. Quantitative feedback robust control for direct drive electro-hydraulic servo rotary vane steering gea[J]. Journal of Jilin University (Engineering and Technology Edition), 2011, 41(3): 670-675. [本文引用:1]
[8]	刘军龙, 代晶辉, 吕凤池, 等. 兆瓦级风力机节能型电-液复合变桨距系统的设计与仿真研究[J]. 机床与液压, 2013(15): 1-6. Liu Jun-long, Dai Jing-hui, Lv Feng-chi, et al. Design and simulation study of energy-saving electro-hydraulic composite pitch control system for megawatt-class wind turbine[J]. Machine Tool and Hydraulics, 2013(15): 1-6. [本文引用:1]
[9]	Navaroo R. Performance of an electro-hydrostatic actuator on the F-18 Systems research aircraft[R]. NASA/TM-97-206224. [本文引用:1]
[10]	Kaminaga H, Ono J, Shimoyama Y, et al. Anthropomorphic robot hand with hydrostatic cluster actuator and detachable passive wire mechanism[C]∥IEEE-RAS International Conference on Humanoid Robots, Humanoids, 2010: 1-6. [本文引用:1]
[11]	刘金琨, 孙富春. 滑模变结构控制理论及其算法研究与进展[J]. 控制理论与应用, 2007, 24(3): 407-418. Liu Jin-kun, Sun Fu-chun. Research and development on theory and algorithms of sliding mode control[J]. Control Theory and Applications, 2007, 24(3): 407-418. [本文引用:1]
[12]	Bonchis A, Corke P I, Rye D C, et al. Brief variable structure methods in hydraulic servo systems control[J]. Automatica, 2001, 37(4): 589-595. [本文引用:1]
[13]	Alle N, Hiremath S S, Makaram S, et al. Review on electro hydrostatic actuator for flight control[J]. International Journal of Fluid Power, 2016: 1-21. [本文引用:1]
[14]	Zhang H, Liu X, Wang J, et al. Robust H_∞ sliding mode control with pole placement for a fluid power electrohydraulic actuator (EHA) system[J]. The International Journal of Advanced Manufacturing Technology, 2014, 73(5): 1095-1104. [本文引用:1]
[15]	Sarpturk S, Istefanopulos Y, Kaynak O. On the stability of discrete-time sliding mode control systems[J]. IEEE Transactions on Automatic Control, 2003, 32(10): 930-932. [本文引用:1]
[16]	Furuta K. Sliding mode control of a discrete system[J]. Systems & Control Letters, 1990, 14(2): 145-152. [本文引用:1]
[17]	Chan C Y. Servo-systems with discrete-variable structure control[J]. Systems and Control Letters, 1991, 17(4): 321-325. [本文引用:1]
[18]	Gao W, Wang Y, Homaifa A. Discrete-time variable structure control systems[J]. IEEE Transactions on Industrial Electronics, 1995, 42(2): 117-122. [本文引用:2]
[19]	杨晨. 电站调节阀门直驱式电液执行器的仿真和实验研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2016. Yang Chen. Simulation and experiment research of the direct-drive electro-hydraulic actuator of regulating valves[D]. Harbin: School of Mechatoronics Engineering, Harbin Institute of Technology, 2006. [本文引用:1]
[20]	Wang X, Chen Z, Yuan Z. Design and analysis for new discrete tracking-differentiators[J]. Applied Mathematics, 2003, 18(2): 214-222. [本文引用:1]
[21]	Wang X, Chen Z, Yang G. Finite-time-convergent differentiator based on singular perturbation technique[J]. IEEE Transactions on Automatic Control, 2007, 52(9): 1731-1737. [本文引用:1]
[22]	Sivaramakrlshnan A Y. Design of variable-structure load-frequency controller using pole assignment technique[J]. International Journal of Control, 1984, 40(3): 487-498. [本文引用:1]

2009

0.0

... 0 引言直驱式容积控制电液伺服系统(Direct drive volume control, DDVC)是一种新型液压伺服系统,随着电机伺服技术不断发展,它得到了越来越广泛的应用^[1,2,3] ...

2014

0.0

2011

0.0

2005

0.0

... DDVC系统充分发挥伺服电动机的特性,采用调节电动机旋转方向和转速的方法来控制压力油的输出方向和流量大小^[4] ...

2005

0.0