考虑侧风干扰的电子稳定控制系统执行器故障诊断

引用本文

王德军, 魏薇郦, 鲍亚新. 考虑侧风干扰的电子稳定控制系统执行器故障诊断[J].吉林大学学报（工学版）, 2018,48(5): 1548-1555
WANG De-jun, WEI Wei-li, BAO Ya-xin. Actuator fault diagnosis of ESC system considering crosswind interference[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(5): 1548-1555 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170729
Permissions

考虑侧风干扰的电子稳定控制系统执行器故障诊断

王德军^1,², 魏薇郦², 鲍亚新²

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.吉林大学通信工程学院, 长春 130022

作者简介:王德军(1970-),男,副教授,博士.研究方向:复杂系统控制、诊断及容错控制.E-mail:djwang@jlu.edu.cn

基金:国家重点研发计划项目(2016YFB0101102);国家自然科学基金国际(地区)合作与交流重点项目(61520106008)

摘要

考虑侧风干扰研究了车辆稳定控制系统的执行器故障诊断算法。建立了带有侧风干扰和执行器故障的车辆七自由度整车模型。为实现侧风干扰存在时ESC系统执行器故障诊断,利用微分几何方法对系统进行微分同胚变换,使得不可测干扰转为可测输入以便干扰解耦。针对变换后系统设计执行器故障观测器,根据残差将执行器故障定位到某一车轮上,并得到实际执行器故障估计值。最后,通过仿真实验验证了该方法的有效性。

关键词: 自动控制技术; 车辆工程; 故障诊断; 微分几何; 执行器; 干扰; 电子稳定控制系统; 观测器

中图分类号:U461,TP273 文献标志码:A 文章编号:1671-5497(2018)05-1548-08

Actuator fault diagnosis of ESC system considering crosswind interference

WANG De-jun^1,², WEI Wei-li², BAO Ya-xin²

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.College of Communication Engineering, Jilin University, Changchun 130022, China

Abstract

The algorithm of actuator Fault Diagnosis (FD) of the vehicle Electronic Stability Control (ESC) system is studied. A seven-degree-of -freedom model of the vehicle with crosswind and actuator failure is built to obtain the information of the actual actuator failure. In order to realize the actuator FD of the ESC system in the presence of crosswind interference, a differential homeomorphic transformation is executed so that the undetectable interference is transformed into the measurable input of the system. Subsequently, the observer for actuator FD is proposed corresponding to the transformed system. The actuator fault can be positioned on a certain wheel by the residual, and the actual actuator failure estimation is obtained. The effectiveness of the method is verified by simulation.

Keyword: automatic control technology; vehicle engineering; fault diagnosis; differential geometry; actuator; disturbance; electronic stability control system; observer

文章图片

0 引言

电子稳定控制 (Electronic stability control, ESC) 系统是目前汽车上广泛应用的主动安全控制系统, 对车辆行驶的安全性发挥着重要作用。目前ESC系统故障诊断可分为传感器故障诊断和执行器故障诊断两类, 多数针对传感器故障。在ESC系统中, 执行器作用尤为重要。ESC系统的执行器主要是指每个轮附近的制动系统, 决定着电子控制单元ECU发出的命令能否被响应, 如果执行器故障, 整个ESC系统将失效, 不能保证车辆的安全性。目前针对ESC系统执行器故障诊断的成果相对较少。文献[1]对液压控制单元建立等效参数化模型, 利用BP神经网络实现液压单元的故障诊断。文献[2]对液压制动系统的故障模式进行了分析, 利用故障树的方法查找故障的部位, 仅仅定性分析故障。文献[3]通过分析冗余关系, 通过建立针对汽车执行器故障的残差, 实现故障的检测与隔离。现有成果针对液压执行机构的故障诊断在增加系统诊断复杂性的同时只考虑局部的执行器故障诊断。本文提出的基于整车全局模型的ESC系统执行器故障诊断方法能直接得到故障信息, 简化了诊断过程。

目前, 针对ESC系统的故障诊断存在两个难点:一是外部干扰的影响, 如侧风干扰等影响; 二是实际执行器故障信息的获得。文献[1, 2, 3]虽然对ESC系统执行器故障进行了诊断, 但都未考虑干扰的存在, 而行驶中的车辆必然会受到由于周围空气流经车外表面而产生的气动力和力矩的影响, 因此, 考虑侧风干扰的ESC系统执行器故障诊断十分必要。通常, ESC采用分层控制的思想, 即通过设计上层控制器得到满足系统控制要求的虚拟输入(一般为一组力或力矩), 下层控制器负责将虚拟输入分配到实际执行器上, 输出期望的力或力矩^[4]。由于复杂的分层控制算法限制, ESC系统的执行器故障诊断通常在上层控制算法的基础上进行, 得到的故障信息只限于虚拟执行器故障信息^[5], 下一步的容错控制仍要考虑中间层和下层的算法设计, 增加了研究的复杂性, 如果能够得到实际执行器故障信息(受故障影响的轮胎力), 容错控制就变得简单。

针对上述两个问题, 本文在考虑侧风干扰的情况下, 先利用微分几何工具对系统进行微分同胚变换达到抗扰目的, 再通过建立执行器故障增广观测器, 实现执行器故障诊断, 并得到实际执行器故障的估计值。

1 汽车模型及模型分解

1.1 车辆七自由度模型

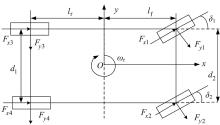
七自由度整车模型是在汽车稳定控制中广泛应用的模型, 如图1所示。在七自由度车辆模型中, 车辆运动状态包括车辆的纵向速度、侧向速度、横摆角速度和4个轮胎的转动。七自由度车辆动力学模型忽略了汽车行驶过程中车身侧倾对和俯仰对其动力学特性的影响, 忽略了空气阻力对车辆运动的影响, 将整车看作一个刚体, 简化描述车辆动力学的方程。由汽车的动力学方程与运动方程可整理成如下状态方程:

$\{\begin{array}{l} {\overset{\cdot}{v}}_{x} = ω_{r} v_{y} + \frac{1}{m} u_{1} \\ {\overset{\cdot}{v}}_{y} = - ω_{r} v_{x} + \frac{1}{m} u_{2} \\ {\overset{\cdot}{ω}}_{r} = \frac{1}{I_{z}} u_{3} \end{array} (1)$

式中: $m$ 为汽车总质量; $v_{x}$ 为纵向车速; $v_{y}$ 为横向车速; $ω_{r}$ 为横摆角速度; $I_{z}$ 为整车绕车辆坐标系z轴的转动惯量; u₁=∑ F_x; u₂=∑ F_y; u₃=∑ M_z看作系统的虚拟输入。

	Figure Option View Download New Window
	图1 七自由度整车模型Fig.1 Seven-degree vehicle model

本文采用前轮转向车辆模型, 前轮为主动转向轮, 转向角相等, δ ₁=δ ₂=δ ; 后轮为从动轮, δ ₃=δ ₄=0。∑ F_x、∑ F_y、∑ M_z的表达式为:

$\{\begin{array}{l} \sum F_{x} = (F_{x 1} + F_{x 2}) \cos δ - (F_{y 1} + F_{y 2}) \sin δ + \\ F_{x 3} + F_{x 4} \\ \sum F_{y} = (F_{x 1} + F_{x 2}) \sin δ + (F_{y 1} + F_{y 2}) \cos δ + \\ F_{y 3} + F_{y 4} \\ \sum M_{z} = l_{f} (F_{x 1} + F_{x 2}) \sin δ + l_{f} (F_{y 1} + F_{y 2}) \cos δ - \\ l_{r} (F_{y 3} + F_{y 4}) - l_{s} (F_{y 1} - F_{y 2}) \sin δ + \\ l_{s} (F_{x 1} - F_{x 2}) \cos δ + l_{s} (F_{x 3} - F_{x 4}) \end{array} (2)$

式中: $l_{s}$ 为汽车轮距的一半; $l_{f}$ 为汽车质心到前轴的距离; $l_{r}$ 为汽车质心到后轴的距离; $F_{xi} 、 F_{yi}$ 分别为某车轮在其轮胎坐标系x(即纵向)、y(即侧向)方向上的力。

1.2 执行器故障及干扰模型建立

本文研究的故障情况主要针对某一车轮执行器故障, 导致制动力突然变化。

车轮动力学方程为:

$F_{xi} \cdot R_{l i} + J_{i} \cdot {\overset{\cdot}{ω}}_{i} - T_{t i} + T_{b i} = 0 (3)$

在第 $i (i = 1, 2, \dots, 4)$ 个车轮上, $J_{i}$ 为转动惯量, $T_{t i}$ 为驱动力矩, $T_{b i}$ 为制动力矩, $R_{l i}$ 为负载半径。由式(3)可以看出, 制动力的变化会对轮胎纵向力产生影响。轮胎是联接车体与路面的唯一部件, 为了获得轮胎力, 本文采用郭孔辉院士提出的统一指数轮胎模型^[6]。

汽车轮胎的侧向力是在汽车行驶过程中由于路面的侧向倾斜、侧向风或者曲线行驶时的离心力等的作用而产生的。轮胎侧偏角较小时, 轮胎的侧向力与轮胎的侧偏力是数值相等的反作用力, 轮胎的侧偏力与侧偏角成正比, 因此轮胎的侧向力与轮胎的侧偏角也成正比, 可表示为^[7]:

$\{\begin{array}{l} F_{y 1} = F_{y 2} = C_{α} α_{f} \\ F_{y 3} = F_{y 4} = C_{α} α_{r} \end{array} (4)$

执行器故障对轮胎侧偏角影响很小, 故此本文忽略故障产生时轮胎侧向力的变化。单一执行器故障是最常见的情况, 本文主要讨论这种情况。出现单一执行器故障时, 该轮纵向力变为:

$F_{xi m} = F_{xi} + q_{i} (5)$

式中: $q_{i}$ 为执行器故障引起的轮胎纵向力变化值, i∈ [1, 4]分别表示车的左前轮、右前轮、左后轮、右后轮。

综合式(2)(5), 得到故障后系统虚拟输入为:

$u_{m} = u + K_{i} q_{i} (6)$

式中: $u_{m} = {[\begin{array}{l} u_{m 1} & u_{m 2} & u_{m 3} \end{array}]}^{T}$ 为引入故障后系统的虚拟输入; $u = {[\begin{array}{l} u_{1} & u_{2} & u_{3} \end{array}]}^{T}$ 为无故障时的虚拟输入; 对应故障分布向量 $K_{i}$ 为:

$\begin{array}{l} K_{1} = {[\begin{array}{l} \cos δ & \sin δ & l_{f} \sin δ + l_{s} \cos δ \end{array}]}^{T} \\ K_{2} = {[\begin{array}{l} \cos δ & \sin δ & l_{f} \sin δ - l_{s} \cos δ \end{array}]}^{T} \\ K_{3} = {[\begin{array}{l} 1 & 0 & l_{s} \end{array}]}^{T} \\ K_{4} = {[\begin{array}{l} 1 & 0 & - l_{s} \end{array}]}^{T} \end{array}$

对于系统(1), 忽略风压中心位置的变化, 并且假设车辆经受稳态侧风, 且假设侧向风方向垂直于车身纵断面, 在汽车横摆角速度较小的情况下, 侧风在车体上产生的干扰侧向力为 $F_{y w} = \frac{1}{2} εS V_{\infty}^{2} 。$ 其中, $ε$ 为空气密度; $S$ 为车辆位于侧风区域的侧向面积; $V_{\infty}$ 为合成气流的相对速度, $V_{\infty}^{2} = V^{2} + V_{w}^{2}, V$ 为车辆行驶速度, $V_{w}$ 为侧风速度。侧风产生的干扰侧向力主要影响整车的侧向合力, 因此侧风干扰通过 $u_{2}$ 作用在车辆系统上^[8]。

综上, 考虑某单一执行器故障和干扰存在时的汽车速度横摆模型为:

$\{\begin{array}{l} {\overset{\cdot}{v}}_{x} = ω_{r} v_{y} + \frac{1}{m} u_{1} + \frac{K_{i 1}}{m} q_{i} \\ {\overset{\cdot}{v}}_{y} = - ω_{r} v_{x} + \frac{1}{m} u_{2} + \frac{K_{i 2}}{m} q_{i} + F_{y w} \\ {\overset{\cdot}{ω}}_{r} = \frac{1}{I_{z}} u_{3} + \frac{K_{i 3}}{I_{z}} q_{i} \\ y_{1} = v_{x} \\ y_{2} = v_{y} \\ y_{3} = ω_{r} \end{array} (7)$

2 系统变换

车辆ESC系统具有复杂的非线性, 对干扰与故障间的解耦十分不利。本文采用微分几何方法进行系统变换, 有以下两个优点:①侧风产生的干扰与车速、风速有关, 该种方法不用考虑干扰的具体形式; ②该方法使得不可测的干扰转变为子系统的可测输入, 为干扰解耦的观测器设计提供了便利。

根据式(7), 考虑执行器故障与干扰的车辆七自由度模型符合如下仿射性非线性系统的形式:

$\{\begin{array}{l} \overset{\cdot}{x} = f (x) + \overset{m}{\sum_{i = 1}} g_{i} (x) u + l (x) q + p (x) w \\ y = x \end{array} (8)$

式中:对应于系统(7)状态变量 $x = {[\begin{array}{l} v_{x} & v_{y} & w_{r} \end{array}]}^{T}; f (x) = {[\begin{array}{l} w_{r} v_{y} & - w_{r} v_{x} & 0 \end{array}]}^{T};$ 控制输入 $u = {[\begin{array}{l} u_{1} & u_{2} & u_{3} \end{array}]}^{T}; g (x) = diag {\frac{1}{m}, \frac{1}{m}, \frac{1}{I_{z}}}; l = {[\begin{array}{l} \frac{1}{m} K_{i 1} & \frac{1}{m} K_{i 2} & \frac{1}{I_{z}} K_{i 3} \end{array}]}^{T};$ 单一故障信号 $q \in R; p = {[\begin{array}{l} 0 & 1 & 0 \end{array}]}^{T};$ 干扰信号 $w = F_{y w} \in R 。$

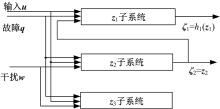
文献[9]提出了能够利用微分几何方法对一类非线性系统进行有干扰存在时故障诊断的必要条件。当该条件存在时, 就能找到包含在 $P^{⊥}$ 中的由精确微分局部张成的最大能观对偶分布 $o . c . a . (({Σ^{P}}_{*})^{⊥}),$ 根据该分布可以得选择变换坐标。在新的坐标系下系统变为式(9)。该式是局部弱能观的。

$\begin{array}{l} {\overset{\cdot}{z}}_{1} = f_{1} (z_{1}, z_{2}) + g_{1} (z_{1}, z_{2}) u + l_{1} (z_{1}, z_{2}) q \\ {\overset{\cdot}{z}}_{2} = f_{2} (z_{1}, z_{2}, z_{3}) + g_{2} (z_{1}, z_{2}, z_{3}) u + \\ l_{2} (z_{1}, z_{2}, z_{3}) q + p_{1} (z_{1}, z_{2}, z_{3}) w \\ {\overset{\cdot}{z}}_{3} = f_{3} (z_{1}, z_{2}, z_{3}) + g_{3} (z_{1}, z_{2}, z_{3}) u + \\ l_{3} (z_{1}, z_{2}, z_{3}) q + p_{2} (z_{1}, z_{2}, z_{3}) w \\ ζ_{1} = h_{1} (z_{1}) \\ ζ_{2} = z_{2} (9) \end{array}$

根据式(9)得到如图2所示的系统框图。

	Figure Option View Download New Window
	图2 变换后系统框图Fig.2 System block diagram after transformation

对系统框图进行分析, $ζ_{2} = z_{2}$ 可以看作 $z_{1}$ 子系统的独立输入, 它包含了不可测干扰对系统的影响, $z_{1}$ 子系统就可以看作只受故障信号 $q 、输入 u$ 和可测输入影响(见图2), 只需对3输入的 $z_{1}$ 子系统进行状态观测器设计, 得到的观测器残差对干扰是解耦的。

针对系统(8), 通过计算可知包含的最小不变分布为:

${Σ^{P}}_{*} = span {{[\begin{array}{l} 0 & 1 & 0 \end{array}]}^{T}}$

由精确微分张成的零化子为:

$({Σ^{P}}_{*})^{⊥} = span {d v_{x}, d ω_{r}}$

同时, 注意到 $span {d h} \supset ({Σ^{P}}_{*})^{⊥},$ 所以有 $o . c . a . (({Σ^{P}}_{*})^{⊥}) = ({Σ^{P}}_{*})^{⊥} 。$ 满足 $span {l} ⊄ [o . c . a . (({Σ^{P}}_{*})^{⊥} {)]}^{⊥} 。$ 由此可以得到微分同胚变换为:

$z_{1} = [\begin{array}{l} v_{x} \\ ω_{r} \end{array}]$

在新的坐标系下系统(8)变为:

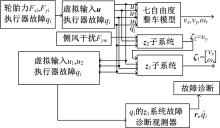
$\begin{array}{l} \begin{array}{l} {\overset{\cdot}{z}}_{1} = [\begin{array}{l} {\overset{\cdot}{z}}_{11} \\ {\overset{\cdot}{z}}_{12} \end{array}] = [\begin{array}{l} z_{12} z_{2} + \frac{1}{m} u_{1} + \frac{K_{i 1}}{m} q_{i} \\ \frac{1}{I_{z}} u_{3} + \frac{K_{i 3}}{I_{z}} q_{i} \end{array}] \\ ζ_{1} = [\begin{array}{l} z_{11} \\ z_{12} \end{array}] (10) \end{array} \\ \{\begin{array}{l} {\overset{\cdot}{z}}_{2} = - z_{12} z_{11} + \frac{1}{m} u_{2} + \frac{K_{i 2}}{m} \cdot q_{1} + F_{y w} \\ ζ_{2} = z_{2} \end{array} \\ (11) \end{array}$

3 基于观测器的故障诊断

4个轮单独发生故障时, 可以得到4个不同的形如式(10)的系统。在观测器设计时, 对4个不同的z₁子系统的执行器故障系统进行观测器的设计(见图3)。通过上述分析观测器的残差对干扰是解耦的, 观察4个残差可以判断故障发生轮的位置。同时, 根据增广系统观测器可以得到实际执行器故障值的估计值。

	Figure Option View Download New Window
	图3 车辆执行器故障诊断流程图Fig.3 Vehicle diagram of actuator fault diagnosis

执行器发生故障时, 本文车辆非线性待观测系统(11)可转换成如下形式:

$\{\begin{array}{l} \overset{\cdot}{x} = φ (x, u) + E_{ai} q_{i} \\ y = x \end{array} (12)$

式中: $E_{ai}$ 为故障分布向量; $q_{i} (i \in [1, 4])$ 为未知的执行器故障。

对应于系统(10), $q_{1} 、 q_{2} 、 q_{3} 、 q_{4}$ 对应的故障分布向量为:

$E_{a 1} = {[\begin{array}{l} \frac{\cos δ}{m} & \frac{l_{f} \sin δ + l_{s} cosδ}{I_{z}} \end{array}]}^{T},$

$E_{a 2} = {[\begin{array}{l} \frac{\cos δ}{m} & \frac{l_{f} \sin δ - l_{s} cosδ}{I_{z}} \end{array}]}^{T},$

$E_{a 3} = {[\begin{array}{l} \frac{1}{m} & \frac{l_{s}}{I_{z}} \end{array}]}^{T}, E_{a 4} = {[\begin{array}{l} \frac{1}{m} & - \frac{l_{s}}{I_{z}} \end{array}]}^{T} 。$

状态变量 $x = [\begin{array}{l} z_{11} \\ z_{12} \end{array}],$ 非线性部分 $φ (x, u) = {[\begin{array}{l} z_{12} z_{2} + \frac{1}{m} u_{1} & \frac{1}{I_{z}} u_{3} \end{array}]}^{T} 。$ 其中前轮转角 $δ$ 看作已知量。

假设发生了突变或缓变故障, 即 ${\overset{\cdot}{q}}_{i} = 0 。$ 有如下主要结果。

定理:针对满足Lipschitz条件 $‖ φ (x_{1}, u) - φ (x_{2}, u) ‖ \leq γ ‖ x_{1} - x_{2} ‖$ 的系统(13), 针对 $q_{i} (i \in [1, 4])$ 建立4个如下形式的状态观测器:

$\{\begin{array}{l} [\begin{array}{l} \overset{\cdot}{\hat{x}} \\ {\overset{\cdot}{\hat{q}}}_{i} \end{array}] = [\begin{array}{l} 0 & E_{ai} \\ 0 & 0 \end{array}] [\begin{array}{l} x \\ q_{i} \end{array}] + [\begin{array}{l} φ (x, u) \\ 0 \end{array}] + \\ L_{i} (y (t) - \hat{y} (t)) \\ \hat{y} (t) = \hat{x} \end{array} (13)$

设残差为 $r_{i} (t) = {[\begin{array}{l} y - \hat{y} & q_{i} - {\hat{q}}_{i} \end{array}]}^{T} (i \in [1, 4]$ ), 在 $r_{1} 、 r_{2} 、 r_{3} 、 r_{4}$ 中, 若 $\lim_{t \to \infty} r_{i} = 0,$ 则故障发生在第i个轮, 故障值为 $q_{i} = \lim_{t \to \infty} {\hat{q}}_{i} 。$

证明:

以故障 $q_{1}$ 为例进行证明。对故障 $q_{1}$ 建立增广系统如下:

$\{\begin{array}{l} [\begin{array}{l} \overset{\cdot}{x} \\ {\overset{\cdot}{q}}_{1} \end{array}] = [\begin{array}{l} 0 & E_{a 1} \\ 0 & 0 \end{array}] [\begin{array}{l} x \\ q_{1} \end{array}] + [\begin{array}{l} φ (x, u) \\ 0 \end{array}] \\ y = [\begin{array}{l} I & 0 \end{array}] [\begin{array}{l} x \\ q_{1} \end{array}] \end{array} (14)$

令 $\bar{x} = {[\begin{array}{l} x & q_{1} \end{array}]}^{T}, \bar{A} = [\begin{array}{l} 0 & E_{a 1} \\ 0 & 0 \end{array}], \bar{φ} (\bar{x}, u) = {[\begin{array}{l} φ (x, u) & 0 \end{array}]}^{T}, \bar{C} = [\begin{array}{l} I & 0 \end{array}],$ 则系统变为:

$\{\begin{array}{l} \overset{\cdot}{\bar{x}} = \bar{A} \bar{x} + \bar{φ} (\bar{x}, u) \\ y = \bar{C} \bar{x} \end{array}$

建立形如式(13)状态观测器如下:

$\{\begin{array}{l} \overset{\cdot}{\hat{\bar{x}}} = \bar{A} \hat{\bar{x}} + \bar{φ} (\hat{\bar{x}}, u) + L_{1} (y (t) - \hat{y} (t)) \\ \hat{y} = \bar{C} \hat{\bar{x}} \end{array} (15)$

估计误差为:

$\begin{array}{l} \overset{\cdot}{e} = \overset{\cdot}{\bar{x}} - \overset{\cdot}{\hat{\bar{x}}} (\bar{A} - L_{i} \bar{C}) e + (\bar{φ} (\bar{x}, u) - \\ \bar{φ} (\hat{\bar{x}}, u)) = (\bar{A} - L_{i} \bar{C}) e + Δ \bar{φ} (16) \end{array}$

取李雅普诺夫备选函数 $V = e^{T} Pe,$ 得:

$\begin{array}{l} \overset{\cdot}{V} = {[(\bar{A} - L_{i} \bar{C}) e + Δ \bar{φ}]}^{Τ} Pe + \\ e^{T} P [(\bar{A} - L_{i} \bar{C}) e + Δ \bar{φ}] (17) \end{array}$

由文献[10]中引理和李普希兹条件 $‖ \bar{φ} (\bar{x}, u) - φ (\hat{\bar{x}}, u) ‖ \leq γ ‖ \bar{x} - \hat{\bar{x}} ‖$ 可得:

$\begin{array}{l} \overset{\cdot}{V} = e^{Τ} {(\bar{A} - L_{i} \bar{C})}^{Τ} Pe + e^{Τ} P (\bar{A} - L_{i} \bar{C}) e + \\ e^{Τ} P Δ \bar{φ} + Δ \bar{φ} Pe \leq e^{Τ} {(\bar{A} - L_{i} \bar{C})}^{Τ} Pe + \\ e^{Τ} P (\bar{A} - L_{i} \bar{C}) e + γ^{2} e^{Τ} e + e^{Τ} PPe \leq \\ e^{Τ} [{(\bar{A} - L_{i} \bar{C})}^{Τ} P + P (\bar{A} - L_{i} \bar{C}) + PP + γ^{2} I] e (18) \end{array}$

如果存在 $P$ 和 $L_{i}$ 满足:

${(\bar{A} - L_{i} \bar{C})}^{Τ} P + P (\bar{A} - L_{i} \bar{C}) + PP + γ^{2} I < - P (19)$

则 $\overset{\cdot}{V} < 0,$ 由李雅普诺法判定定理可知, 对于任意非零向量 $e,$ 都有 $\lim_{t \to \infty} e = 0 。$ 因此当故障 $q_{1}$ 发生时, $\lim_{t \to \infty} r_{1} = \lim_{t \to \infty} e = 0$ 且 $\lim_{t \to \infty} {\hat{q}}_{1} = q_{1} 。$

令增益矩阵 $L_{1} = P^{- 1} X, P 和 X$ 通过解与式(19)等效的如下不等式得到:

$[\begin{array}{l} {\bar{A}}^{Τ} P + P \bar{A} - {\bar{C}}^{Τ} X^{Τ} - X \bar{C} + P + γ^{2} I & P \\ P & - I \end{array}] < 0 (20)$

故障 $q_{2} 、 q_{3} 、 q_{4}$ 的观测器建立与 $q_{1}$ 相似, 得到的增益矩阵 $L_{2} 、 L_{3} 、 L_{4} 。 L_{1} 、 L_{2} 、 L_{3} 、 L_{4}$ 各不相等, 所以当故障 $q_{1}$ 单独发生时, 只有 $\lim_{t \to \infty} r_{1} = 0, \lim_{t \to \infty} r_{2} \neq 0, \lim_{t \to \infty} r_{3} \neq 0, \lim_{t \to \infty} r_{4} \neq 0,$ 证毕。

执行器故障诊断过程如下:

(1)4个观测器残差值均为0, 则无故障发生。

(2)4个观测器残差发生突变, 一段时间后只有一个观测器残差稳定在0值, 则该观测器所对应的轮即为故障发生的轮。

(3)判断故障发生轮的位置后, 根据该轮的观测器可以得到实际执行器故障值得估计值。

4 仿真验证

整车的仿真参数如下:汽车的总质量 $m = 1359.8 kg;$ 整车绕车辆坐标系z轴转动惯量 $I_{z} = 1992.54 kg \cdot m^{2};$ 重力加速度 $g = 9.8 m \cdot s^{2};$ 质心高度 $h = 0.512 m;$ 汽车质心到后轴距离 $l_{r} = 1.4852 m;$ 汽车质心到前轴距离 $l_{f} = 1.0628 m;$ 前轮轮距 $d = 1.414 m;$ 空气密度 $ε = 1.2258 kg / m^{3};$ 车辆位于侧风区域的侧向面积 $S = 5.355 m^{2};$ 侧风速度 $V_{w} = 20 m / s 。$

根据定理得到故障观测器的增益矩阵如下:

$\begin{array}{l} L_{1} = [\begin{array}{l} 21000 & 0 \\ 0 & 21000 \\ 44461000 & 22097000 \end{array}], \\ L_{2} = [\begin{array}{l} 21000 & 2000 \\ 2000 & 18000 \\ 49299000 & 23071000 \end{array}], \\ L_{3} = [\begin{array}{l} 21000 & 0 \\ 0 & 21000 \\ 47756000 & 23042000 \end{array}], \\ L_{4} = [\begin{array}{l} 21000 & 0 \\ 0 & 21000 \\ 47756000 & - 23042000 \end{array}] 。 \end{array}$

仿真分析如下:

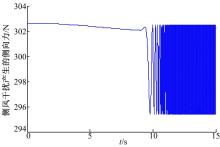
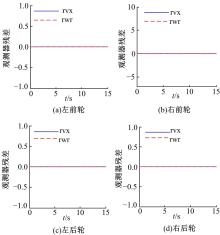
(1)侧风干扰存在, 执行器无故障的情况。根据上述参数的选取, 侧风干扰产生的侧向力如图4所示。图5是4个增广系统观测器的残差, 表示在干扰存在的情况下, 残差始终为0, 可以验证观测器的残差对干扰是解耦的。

	Figure Option View Download New Window
	图4 无故障时侧风干扰产生侧向力Fig.4 Lateral force generated by lateral wind interference without actuator fault

	Figure Option View Download New Window
	图5 有干扰无故障时观测器残差Fig.5 Residual with disturbance and without actuator fault

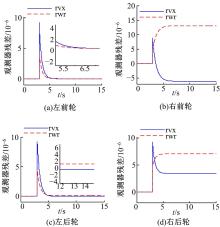
(2)左前轮故障单独发生且侧风干扰存在的情况。图6是该情况下产生的一个与纵向速度相关的侧风干扰侧向力。图7为4个观测器的残差值, 实线为该观测器纵向速度残差值rvx(m/s), 虚线为该观测器横摆角速度残差值rwr(rad/s)。在0~3 s, 无故障产生, 4个观测器的残差均为0; 在3 s时发生缓变故障, 4个观测器残差均发生突变, 而只有左前轮观测器的残差(见图7(a))在7 s左右回到0值, 由此判断出故障轮是左前轮。

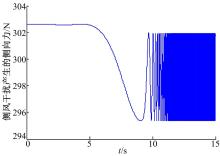	Figure Option View Download New Window
	图6 左前轮故障时侧风干扰产生的侧向力Fig.6 Lateral force generated by lateral wind interference with left front wheel actuator fault

	Figure Option View Download New Window
	图7 左前轮故障时观测器残差Fig.7 Residual with disturbance and left front wheel actuator fault

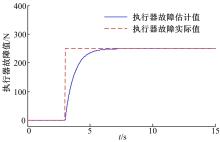
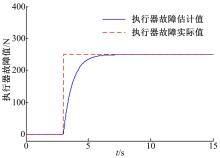
该轮上产生的执行器故障的估计值同时可以由增广系统的观测器得到(见图8)。

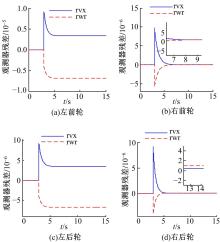
	Figure Option View Download New Window
	图8 左前轮故障时执行器故障估计值Fig.8 Actuator fault estimation with the left front wheel actuator fault

(3)右前轮故障单独发生且侧风干扰存在的情况。图9是该情况下产生的一个与纵向速度相关的侧风干扰侧向力(纵轴数值上与图5不同)。图10为4个观测器的残差值, 实线为该观测器纵向速度残差值rvx(m/s), 虚线为该观测器横摆角速度残差值rwr(rad/s), 在0~3 s, 无故障产生, 4个观测器的残差均为0; 在3 s时发生缓变故障, 4个观测器残差均发生突变, 而只有右前轮观测器的残差(见图10(b))在8 s左右回到0值, 由此判断出故障轮是右前轮。该轮的执行器故障增广系统可以得到故障值的估计值(见图11)。

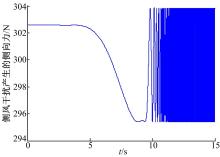	Figure Option View Download New Window
	图9 右前轮故障时侧风干扰产生的侧向力Fig.9 Lateral force generated by lateral wind interference with right front wheel actuator fault

	Figure Option View Download New Window
	图10 右前轮故障时观测器残差Fig.10 Residual with disturbance and right front wheel actuator fault

	Figure Option View Download New Window
	图11 右前轮故障时执行器故障估计值Fig.11 Actuator fault estimation with right front wheel actuator fault

5 结束语

针对汽车的七自由度模型, 本文利用微分几何方法实现了侧风干扰存在时故障诊断, 使不可测干扰变为子系统可测输入, 针对子系统进行非线性观测器设计实现ESC系统执行器故障诊断。由仿真结果可看出, 通过残差能够对汽车执行器故障进行精确的检测与定位, 同时可以直接由观测器得到故障发生轮的执行器故障值的估计值。本文的研究对汽车的容错控制有重要的意义。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	魏峙. BP神经网络在汽车ESP系统故障诊断中的应用[D]. 大连: 大连理工大学控制科学与工程学院, 2015. Wei Zhi. Application of BP neural network in fault diagnosis of automobile ESP system[D]. Dalian: School of Control Science and Engineering, Dalian University of Technology, 2015. [本文引用:2]
[2]	黄伟中, 郭立书, 杨雄. 汽车制动系统故障诊断与性能优化方法[J]. 汽车工程师, 2012(11): 59-61. Huang Wei-zhong, Guo Li-shu, Yang Xiong. Fault diagnosis and performance optimization method of automobile braking system[J]. Automotive Engineers, 2012(11): 59-61. [本文引用:2]
[3]	Dumont P E, Aitouche A, Bayart M. Fault detection of actuator faults for electric vehicle[C]∥2007 IEEE International Conference on Control Applications, Singapore, 2007: 1067-1072. [本文引用:2]
[4]	Johansen T A, Fossen T I. Control allocation—a survey[J]. Automatica, 2013, 49(5): 1087-1103. [本文引用:1]
[5]	王德军, 鲍亚新, 张贤达. 汽车稳定控制系统执行器与传感器故障诊断与估计[J]. 自动化仪表, 2017, 38(4): 41-45. Wang De-jun, Bao Ya-xin, Zhang Xian-da. Fault diagnosis and estimation of actuator and sensor for vehicle stability control system[J]. Process Automation Instrumentation, 2017, 38(4): 41-45. [本文引用:1]
[6]	Guo K, Ren L. A unified semi-empirical tire model with higher accuracy and less parameters[J]. SAE Transactions, 1999, 108: 1513-1520. [本文引用:1]
[7]	Rajamani R. Vehicle Dynamics and Control[M]. Berlin: Springer, 2006. [本文引用:1]
[8]	时晓杰. 侧风影响下车辆侧翻事故的仿真研究与分析[D]. 南京: 东南大学交通学院, 2012. Shi Xiao-Jie. Simulation research and analysis of the vehicle rollover accident under the influence of cross wind[D]. Nanjing: School of Transportation, School of Transportation, 2012. [本文引用:1]
[9]	de Persis C, Isidori A. A geometric approach to nonlinear fault detection and isolation[J]. IEEE Transactions on Automatic Control, 2001, 46(6): 853-865. [本文引用:1]
[10]	Chen M, Zhou D, Shang Y. Integrity control of chaotic systems[J]. Physics Letters A, 2006, 350(3/4): 214-220. [本文引用:1]

2015

0.0

... 文献[1]对液压控制单元建立等效参数化模型,利用BP神经网络实现液压单元的故障诊断 ...

... 文献[1,2,3]虽然对ESC系统执行器故障进行了诊断,但都未考虑干扰的存在,而行驶中的车辆必然会受到由于周围空气流经车外表面而产生的气动力和力矩的影响,因此,考虑侧风干扰的ESC系统执行器故障诊断十分必要 ...

2012

0.0

... 文献[2]对液压制动系统的故障模式进行了分析,利用故障树的方法查找故障的部位,仅仅定性分析故障 ...

2007

0.0

... 文献[3]通过分析冗余关系,通过建立针对汽车执行器故障的残差,实现故障的检测与隔离 ...

2013

0.0

... 通常,ESC采用分层控制的思想,即通过设计上层控制器得到满足系统控制要求的虚拟输入(一般为一组力或力矩),下层控制器负责将虚拟输入分配到实际执行器上,输出期望的力或力矩^[4] ...

2017

0.0

... 由于复杂的分层控制算法限制,ESC系统的执行器故障诊断通常在上层控制算法的基础上进行,得到的故障信息只限于虚拟执行器故障信息^[5],下一步的容错控制仍要考虑中间层和下层的算法设计,增加了研究的复杂性,如果能够得到实际执行器故障信息(受故障影响的轮胎力),容错控制就变得简单 ...

1999

0.0

... 轮胎是联接车体与路面的唯一部件,为了获得轮胎力,本文采用郭孔辉院士提出的统一指数轮胎模型^[6] ...

2006

0.0

... 轮胎侧偏角较小时,轮胎的侧向力与轮胎的侧偏力是数值相等的反作用力,轮胎的侧偏力与侧偏角成正比,因此轮胎的侧向力与轮胎的侧偏角也成正比,可表示为^[7]: ...

2012

0.0

... 侧风产生的干扰侧向力主要影响整车的侧向合力,因此侧风干扰通过 u2作用在车辆系统上^[8] ...

2001

0.0

... 文献[9]提出了能够利用微分几何方法对一类非线性系统进行有干扰存在时故障诊断的必要条件 ...

2006

0.0

... 由文献[10]中引理和李普希兹条件 ‖φ-(x-,u)-φ(x-^,u)‖≤γ‖x--x-^‖可得: ...