吉林大学汽车运输研究所开发研制的转向架参数测试台不仅具有对一系、二系的垂向、纵向、横向静态刚度进行测试的功能,同时由于试验台下部双六自由度运动模拟系统可实现空间六自由度运动模拟,因此该试验台还可实现动刚度、回转力矩等参数的测定^{[ 5]}。

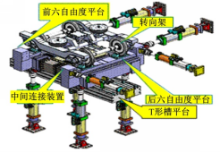
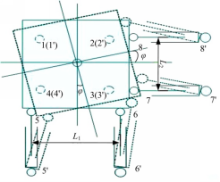
回转阻力矩测试时,只需实现转向架在水平面的旋转运动,不需要下部双六自由度平台其余自由度的运动模拟,故通过中间连接装置将双六自由度平台联接成一体。另外利用安装在下T形槽平台上的横向约束心轴墩,实现对转向架的横向约束,防止转向架横向移动,如图1所示。将转向架固定在六自由度运动平台上,将车体及加载砝码放置在待测转向架上实现空车和重车工况(车体及加载砝码未在图1中标注),通过固定装置限制车体在水平面的旋转运动。各作动器活塞杆在控制系统指令下进行伸缩移动,六自由度运动平台带动转向架作回转运动,回转力矩测试示意图如图2所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 回转力矩测试虚拟样机Fig.1 Virtual prototype for rotary torque test

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 回转力矩测试示意图Fig.2 Schematic diagram of rotary torque test

假设车体与转向架相对角位移为φ时,回转力矩为M,回转力矩可表示为

M=M₁+M₂=F₁L₁+F₂L₂(1)

式中:F₁为纵向作动器的作用力;F₂为横向作动器的作用力。

通过分别读取转台状态下及装载转向架状态下的纵向作动器与横向作动器测力传感器对应的F₁及F₂值,并代入式(1)中求得转动平台及转向架整体的回转力矩,整体回转力矩与转动平台本身回转力矩之差即是转向架回转力矩。利用加载砝码分级改变加载载荷来测定转向架随载荷变化的回转阻力矩特性,可以绘制出转向架回转力矩-角位移关系曲线。

六自由度运动模拟平台的回转运动是实现准确测试转向架回转力矩的关键部分之一,而运动学反解是实现运动模拟平台回转运动的首要任务。本文引入基于欧拉角的齐次变化矩阵及Simulink仿真环境建立了平台位姿反解实时模型,为实现转向架回转力矩测试奠定基础。

2.1 位姿反解模型

本文结合六自由度运动模拟系统结构,选取六自由度平台垂向4个下铰链点所在平面中心为静坐标原点,轮对与夹具两个切点的中点为六自由度平台的体坐标系原点,静坐标系与体坐标系均选取列车的行驶运动方向为X轴,横向运动方向为Y轴,铅直方向为Z轴。本文利用齐次坐标来表示铰链点的空间位置,引入齐次变换矩阵来表示体坐标系原点相对于静坐标系原点在空间的平移和转动,用广义坐标P=(θ,ϕ,φ,x,y,z)来描述体坐标相对于静坐标的位姿,θ、ϕ、φ分别为体坐标系相对于静坐标系的绕x、y、z的姿态角,x、y、z分别为体坐标系相对于静坐标系沿X、Y、Z坐标轴的平移量^{[ 6, 7, 8]}。

结合结构参数,8个作动器上铰链点 A _i( i=1,2,…,8)体坐标用矩阵形式表示为

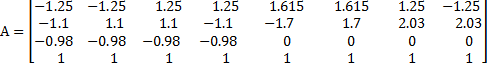(2)

8个作动器下铰链点 B _i( i=1,2,…,8)静坐标用矩阵形式表示为

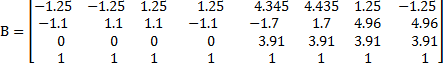(3)

采用 ZYX旋转变换方式时,齐次变换矩阵 T表示为^{[ 9, 10]}

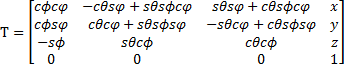
式中:“ c”代表 cos;“ s”代表 sin。

各作动器上、下两铰链点之间位置向量关系为^{[ 11]}

L _i= T· A _i- B _i ( i=1,2,…,8) (4)

进而伸缩量可表示为

Δ L i=‖ T· A i- B i‖-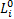

(5)

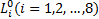
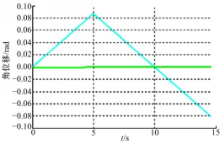
式中: 为作动器初始长度。

2.2 位姿解算

根据转向架回转力矩测试技术要求,六自由度运动模拟平台需绕 Z轴旋转-5 °~5 °,角速度为1 °/s,故 φ取值为[-5 °,5 °]。平台从初始位置以恒定角速度顺时针转动至5 °,再逆时针回转至-5 °,试验中角位移随时间变化趋势见图3。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 角位移随时间变化趋势Fig.3 Changing trend of angle with time

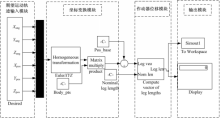
在位姿反解数学模型基础上,本文建立了Simulink位姿反解仿真模型,包括期望运动轨迹输入模块、坐标变换模块、作动器位移模块及数据输出模块^{[ 12, 13]},如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 Simulink位姿反解仿真模型Fig.4 Inverse kinematics Simulink simulation solution model

通过期望运动轨迹输入模块设置P=(0,0,φ,0,0,0),φ借助于三角波发生器模块生成。采用欧拉算法,设置时间步长为0.01 s,运行反解模型,8个作动器位移实时解算结果见表1,由于数据庞大且文章篇幅有限,表1中只显示了每阶段过渡段数据。从表1中可以看出,作动器1~4的伸缩量始终一致,8个作动器的伸缩量成非线性变化。0~5 s过程中,8个作动器伸缩量一直呈上升趋势,5 s时作动器伸缩量达到最大值,此后5~10 s过程中伸缩量一直处于回降趋势,且与0~5 s过程中作动器伸缩量关于 t=5 s对称。10 s时作动器伸缩量为0,即平台回到初始位置。此后5 s内伸缩量绝对值呈上升趋势,且伸缩量与5~10 s过程中的伸缩量关于 t=10 s对称。

表1

Table 1

表1(Table 1)

表1 作动器位移实时解算结果 Table 1 Real-time solution results of actuators displacement 时间/s 参 数 ΔL1 ΔL2 ΔL3 ΔL4 ΔL5 ΔL6 ΔL7 ΔL8 0 1.44E-05 1.44E-05 1.44E-05 1.44E-05 -0.29667 0.296745 -0.21811 0.218218 0.01 5.76E-05 5.76E-05 5.76E-05 5.76E-05 -0.59326 0.593568 -0.43612 0.436542 0.02 0.00013 0.00013 0.00013 0.00013 -0.88977 0.89047 -0.65403 0.654969 ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ 4.99 3.584179 3.584179 3.584179 3.584179 -137.582 157.1031 -95.2292 121.2637 5.0 3.598541 3.598541 3.598541 3.598541 -137.835 157.4347 -95.3915 121.5303 5.01 3.584179 3.584179 3.584179 3.584179 -137.582 157.1031 -95.2292 121.2637 ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ 9.99 1.44E-05 1.44E-05 1.44E-05 1.44E-05 -0.29667 0.296745 -0.21811 0.218218 10 0 0 0 0 0 0 0 0 10.01 1.44E-05 1.44E-05 1.44E-05 1.44E-05 0.296745 -0.29667 0.218218 -0.21811 ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ ︙ 14.98 3.569846 3.569846 3.569846 3.569846 156.7715 -137.328 120.9971 -95.0668 14.99 3.584179 3.584179 3.584179 3.584179 157.1031 -137.582 121.2637 -95.2292 15 3.598541 3.598541 3.598541 3.598541 157.4347 -137.835 121.5303 -95.3915

表1 作动器位移实时解算结果 Table 1 Real-time solution results of actuators displacement

本文将时间作为自变量,对应的各作动器伸缩量作为因变量,利用MATLAB强大的曲线拟合工具箱cftool^{[ 14]},基于最小二乘法对伸缩量转角及时间进行拟合,进而得到各作动器伸缩量与时间之间的函数关系,即确定各作动器期望运动规律曲线。

从作动器伸缩量随时间变化的散点图的走向中可以看出其符合分段多项式函数,分段区间为[0,5]及[5,10]。通过拟合命令按钮对各作动器实时伸缩量散点图进行分段多项式曲线拟合,选取不同函数拟合类型,并通过查看拟合效果分析参数SSE(和方差)、Adjusted R-square(均方差)、R-square(确定系数)及RMSE(均方根)对拟合效果进行评估。SSE及RMSE越接近于0,说明函数方式选择和拟合越好^{[ 15]};Adjusted R-square及R-square越接近于1,表明曲线拟合效果越好。各作动器第一分段区间伸缩量与时间关系拟合情况如表2所示,第二区间拟合评价情况不再赘述。从表2可以看出,由于作动器1~4二次拟合和三次拟合的效果相差很小,且三次拟合项系数过小,进而选取二次拟合即可。其余4个作动器三次拟合的效果明显比二次拟合效果好,因此作动器5~8伸缩量与时间成三次方程形式。各作动器伸缩量对应的分段多项式函数为

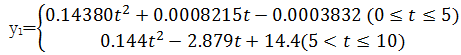(6)

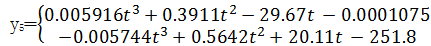(7)

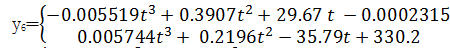(8)

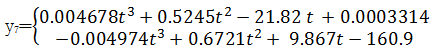(9)

(10)

表2

Table 2

表2(Table 2)

表2 拟合评价指标 Table 2 Fitting evaluation index 参数 作动器1~4 作动器5 作动器6 作动器7 作动器8 2次拟合 3次拟合 2次拟合 3次拟合 2次拟合 3次拟合 2次拟合 3次拟合 2次拟合 3次拟合 和方差 1.484E-005 2.313E-007 0.09903 5.517E-007 11.87 3.247E-006 8.901 0.001458 8.901 0.001458 均方差 1 1 1 1 1 1 1 1 1 1 确定系数 1 1 1 1 1 1 1 1 1 1 均方根 0.0001727 2.157E-005 0.0141 3.332E-005 0.109 8.082E-005 0.09444 0.001209 0.09444 0.001209

表2 拟合评价指标 Table 2 Fitting evaluation index

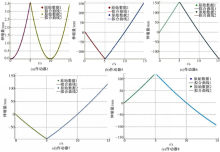
图5为各作动器期望伸缩量及经拟合后得到的期望运动规律曲线。从图5可以看出拟合曲线能准确地逼近离散数据,逼近精度高。目前控制多自由度运动平台的位姿反解实时解算工作主要

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 各作动器伸缩量散点及拟合曲线图Fig.5 Expansion amounts scatter and fitting curve of every actuator

由计算机完成,然后将解算结果(作动器期望伸缩量)送到系统的控制器中,经数/模转换后送给伺服控制系统,各作动器协调工作,平台按预先期望的规律运动。此方法避免了平台运动过程中位姿反解在线计算,节约了计算时间,提高了平台运动精度。同时降低了对计算机性能的要求,减少了成本。对于重复性运动只需保存位姿反解数据,使用时调用数据即可,避免了反复计算,但存在数据容易丢失的问题。本文采用将经曲线拟合后得到的各作动器运动规律曲线作为实际平台的控制输入,通过主控计算机发送指令给伺服作动器,从而使各作动器跟踪所输入的运动曲线,液压缸的实际位移通过位移传感器并经模/数转换后送给计算机,完成闭环伺服控制,最终平台按预先期望的规律运动。

在提出利用转向架综合参数测试台进行转向架回转力矩测试方案的基础上,本文利用齐次矩阵及向量运算建立了转向架回转平台位姿反解数学模型,借助于Simulink模型实现了位姿反解的实时解算,使用MATLAB/cftool曲线拟合工具箱精确地拟合出各作动器伸缩量分段函数曲线,将其做为转向架回转平台的控制输入,为回转力矩测试试验奠定基础。