如何准确获取路面附着系数一直是汽车工业的研究热点^[1]。目前,路面附着系数估计方法有许多种,Yi等^[2]基于电控制动系统实现了对路面附着系数的估计,取得了较好的估计效果。为了进一步提高估计精度,有学者引入了滑模观测器和无偏卡尔曼滤波等研究路面附着系数的估计方法^[3,4,5,6]。但是,如何兼顾估计结果的精度和算法的实时性,仍是研究难点。新型汽车电控系统的出现为路面附着系数的估计提供了更多的思路,如在四轮轮毂电机独立驱动的电动汽车中,可以通过轮毂电机的工作状态获取更多的车辆参数,使得路面附着系数的估计结果更加方便和准确^[7]。

汽车线控转向系统由于取消了方向盘与转向车轮之间的机械连接,其转向角传动比和路感均可以自由设计,极大地提高了汽车转向性能,是未来汽车转向系统的发展趋势和研究热点^[8]。以上文献的研究主要都是在驱动和制动工况下对路面附着系数进行辨识,本文针对线控转向汽车,重点研究转向工况下的路面附着系数估计方法。

首先,建立车辆二自由度动力学模型,具体表示为

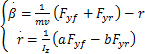(1)

式中:β为质心侧偏角;m为车辆载荷;v为汽车行驶速度;F_{y f}为前轮侧偏力;F_{y r}为后轮侧偏力;r为横摆加速度;I_z为车辆横摆转动惯量;a为车辆质心到前轴距离;b为车辆质心到后轴距离。

利用汽车运动学关系,车轮侧偏角可以描述为

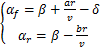(2)

式中:a _f和a _r分别为汽车前、后轮侧偏角;δ为前轮转角。

前、后轮侧偏力采用刷子轮胎模型计算,其公式为F_yi=

(3)式中:F_yi为第i个轮胎的侧向力;μ为路面附着系数;F_zi为第i个轮胎的垂向力;θ_i为拟合系数。

θ_yi=

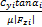(4)

C_yi= 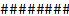(5)式中:C_yi为车轮侧偏刚度;α_i为车轮侧偏角,i= f是前轮侧偏角,i= r为后轮侧偏角。

对式(2)进行求导,可得

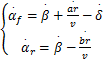(6)

将式(1)~(5)联立可得

(7)

采用扩展卡尔曼滤波实现对路面附着系数的估计,具体分为3步^[4]:首先,建立系统参数和测量方程

(8)式中: x_s( t)为状态变量; x_p( t)为参数变量; u( t)为控制变量; w( t)为过程噪声; y( t)为测量输出; v( t)为测量噪声。

接下来进行参数预测

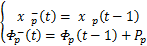(9)

式中: Φ_p( t)和 P_p均为协方差矩阵。

最后是进行参数修正,其方程为

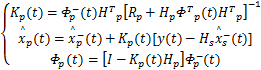(10)

式中: R_p、 H_p和 H_s分别为测量噪声协方差、测量输出对参数变量的偏导数的雅克比矩阵和测量输出对状态变量的偏导数的雅克比矩阵, H_p和 H_s具体表示为 H_p =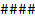

H_s = 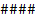结合上面的方程,待估计的状态和参数状态为 x_s( t) =[ α_f, α_r]和 x_p( t) =[ μ_f, μ_r],其中 μ_f为前轮路面附着系数, μ_r为后轮路面附着系数。

考虑到轮胎侧偏角的非线性会对估计精度产生影响,这里引入整车回正力矩信息,从而保证参数和状态的估计精度。

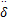
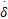
在线控转向系统中,车轮转动由转向电机代替驾驶员完成,即转向电机输出力矩和车轮回正力矩共同作用完成,具体描述为 J_e +B_e =n_g k_i ηi_m +τ(11)式中: J_e为转向系统惯量; B_e为转向系统刚度; n_g为减速机构速比; k_i为电机工作系数; η为电机工作效率; i_m为车辆横摆转动惯量; τ为回正力矩。

由式(11)可知,通过转向过程中的力矩平衡关系可以获取回正力矩信息,同时回正力矩也与前轮转角有密切联系。因此,所估计的状态参数变为 x_s( t) =[ α_f, α_r, τ], x_p( t) =[ μ_f, μ_r]

采用商用软件 CarSim,选取典型试验工况对所提出的路面附着系数估计方法进行验证。

3 .1 中心区试验

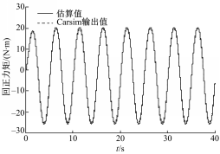
试验车速为100 km/h,转向输入近似于连续正弦,使整车峰值侧向加速度约为0 .2 ×9 .8 m/s²,转向周期为5 s左右,路面附着系数为0 .85。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 中心区试验回正力矩估计结果Fig.1 Estimation result of self-aligning torque on-center test condition

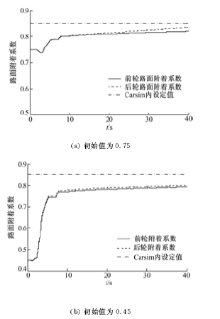
图1是试验过程中的回正力矩估计结果,通过对比可以看出估计值和CarSim输出的实际值基本一致,验证了估计方法的有效性。图2为路面附着系数的初始值为0.75和0.45时前后轮路面附着系数的估计结果。从图2(a)可以看出,提出的估计方法可以很好地估算路面附着系数。在图2(b)中,虽然初始值与实际值相差较大,但是也可以较快地趋近目标值,验证了算法在不同初始值下的鲁棒性。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 中心区试验路面附着系数估计结果Fig.2 Estimation result of road tire friction coefficient on-center test condition

3.2 角阶跃试验

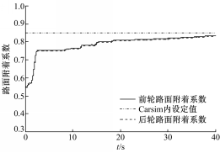
试验车速为80 km/h,方向盘为0.2 s时起跃50°转角,进行角阶跃工况试验,路面附着系数为0.85。图3是转向回正力矩估计结果,实际估计值与Carsim输出值变化趋势和幅值均比较接近,验证了估计方法精度。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 角阶跃试验回正力矩估计结果Fig.3 Estimation result of self-aligning torque on step-angle test condition

图4是路面附着系数估计结果。为了验证不同初始值估计方法的有效性,将初始值设为0.55,从图4曲线可以看出,前后轮路面附着系数估计值趋近Carsim中设置的目标值,说明提出的估计方法具有较高的精度。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 角阶跃试验路面附着系数估计结果Fig.4 Estimation result of road tire friction coefficient on step-angle test condition

研究了整车动力学和基于扩展卡尔曼滤波的路面附着系数估计方法。结合线控转向系统可以较容易地获取转向回正力矩信息的特点,实现对路面附着系数的估计。采用商业软件Carsim对提出的估计方法进行了验证。结果表明,在没有制动工况参与的前提下,提出的方法也可以较好地保证路面附着系数的估算精度。