引用本文
郭洪艳, 陈虹, 高振海, 于海洋, 吉岩. 基于随机算法的级联车速观测器设计. 2014, 44(2): 296-304[GUO Hong-yan, CHEN Hong, GAO Zhen-hai, YU Hai-yang, JI Yan. Design of cascaded vehicle velocity observer based on randomized algorithms. 吉林大学学报(工学版), 2014, 44(2): 296-304]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于随机算法的级联车速观测器设计
郭洪艳1,2, 陈虹1,2, 高振海1, 于海洋2, 吉岩2
1.吉林大学 汽车仿真与控制国家重点实验室,长春 130022
2.吉林大学 通信工程学院,长春 130022
基金:国家自然科学基金重大项目(91220301); 教育部“长江学者和创新团队项目发展计划”创新团队项目(IRT1017); “973”国家重点基础研究发展计划项目(2012CB821202);
摘要

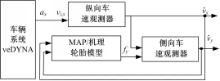
为降低复杂轮胎模型带来的运算负担,首先在数据/机理混合描述的轮胎模型的基础上得到车辆动力学描述并进行了模型验证。然后,采用模块化估计策略,设计非线性级联车速观测器,并利用随机算法对级联车速观测器参数及增益选取进行了讨论。为验证车速观测器的估计效果,在车辆运行的常规和极限工况下进行了仿真研究,并与降阶车速观测器方法及高精度车辆动力学模型进行了对比研究。结果表明,采用随机算法得到的级联车速观测器参数和增益可获得较好的估计效果,同时,采用数据/机理混合建模方法设计观测器可得到较快的计算速度。

关键词: 车辆工程; 级联观测器; 随机算法; 数据/机理建模
中图分类号:TP29 文献标志码:A 文章编号:1671-5497(2014)02-0296-09
Design of cascaded vehicle velocity observer based on randomized algorithms
GUO Hong-yan1,2, CHEN Hong1,2, GAO Zhen-hai1, YU Hai-yang2, JI Yan2
1.State Key Laboratory of Automobile Simulation and Control, Jilin University, Changchun 130022,China
2.College of Communication Engineering, Jilin University, Changchun 130022,China
Fund:
Abstract

In order to reduce the computational cost of complex tyre model, the vehicle dynamics description is obtained based on the mixed data/physics tyre model and the mixed model is validated. Then, the nonlinear cascaded observer is designed using the modular estimation scheme. The selections of parameters and gain of the cascaded observer are discussed using randomized algorithm. For the sake of verifying the estimation results of the vehicle velocities, simulations are carried out under the normal and critical running conditions. The estimation results are compared with the nonlinear reduced-order observer and with the high precision vehicle dynamic model. The simulation results show that the observer parameters and gains obtained from the randomized algorithm are good estimations. Moreover, faster computation speed could be received using data/physics modeling method.

Keyword: vehicle engineering; cascaded observer; randomized algorithm; data/physics modeling
0 引 言

在车辆系统中对于复杂的难以利用机理模型建模的部件或者采用机理模型建模较为复杂的环节,利用数据图表(map)建立输入输出模型是一种简单可行的方法。它是一种朴素的数据存储方法。数据图表是指通过大量稳态实验标定得到的描述某个环节或部件输入输出特性的数据图表。这种方法在车辆控制中已有大量的应用[ 1],如应用在发动机控制系统[ 2]、传动系统[ 3]、车辆稳定性方面[ 4, 5]等。数据图表方法用于车辆系统建模,可有效提高车辆系统主动安全控制算法的在线计算速度。为保证车辆的操纵稳定性及主动安全性,各种车辆主动安全系统相继研制成功,如制动防抱死系统(Anti-lock brake system,ABS)[ 6],电子稳定控制系统(Electronic stability system,ESP)[ 7]和牵引力控制系统(Traction control system,TCS)[ 8]。纵向速度和侧向速度是车辆主动安全系统发挥作用的前提和关键。但纵向车速和侧向车速无法通过传感器测量得到,若简单地采用各车轮纵向速度的加权平均作为纵向车速的估计值,或由侧向加速度的简单积分得到侧向车速,又很难满足车辆主动安全控制对控制精度的要求。因此,近年来车辆速度估计问题日益受到研究人员的重视。在车速估计算法中,轮胎力信息对估计效果有较大影响。目前车速估计中获取轮胎力信息主要通过经验轮胎模型,如Magic Formula模型;半经验轮胎模型,如Uni-Tire模型。经验和半经验轮胎模型可获得较高的模型精度,但二者均存在计算相对复杂的问题。文献[9]在Magic Formula轮胎模型的基础上,采用非线性观测器方法对车辆速度进行估计,并采用输入-状态稳定(Input-to-state stability,ISS)理论对观测器的稳定性进行分析,同时得到观测器增益满足的条件。文献[10]也采用相似的方法对观测器增益选取进行了讨论。由于采用相对复杂的轮胎模型计算轮胎力,使得车速估计的实时性受到影响。同时,这种基于ISS的观测器增益选取方法只是对观测器增益的范围进行界定,并未给出观测器增益的具体取值。随着随机算法[ 11, 12]研究的不断深入,通过蒙特卡罗实验探索车辆车速观测器增益选取将是一条可行之路。

本文为获得与车辆主动安全控制密切相关的车辆速度,进一步提高车辆稳定性控制和车速估计的计算速度,首先建立数据/机理混合描述的轮胎模型,在此基础上得到了车辆动力学描述,并对数据/机理混合描述的车辆模型进行了验证。在此基础上,采用模块化估计策略,设计非线性级联车速观测器,对车辆的纵向速度和侧向速度进行估计。在级联车速观测器ISS的基础上,采用随机算法讨论了车速观测器增益及参数的选取。为验证车速观测器增益的准确性和级联车速观测器的估计效果,在车辆运行的常规和极限工况进行了仿真研究,并与降阶车速观测器方法及车辆动力学软件veDYNA进行了对比。仿真结果表明,在得到较好估计效果的基础上,基于随机算法的级联车速观测器估计效果较好,计算速度较快,具有进一步研究的价值。

1 车辆动力学数据/机理建模

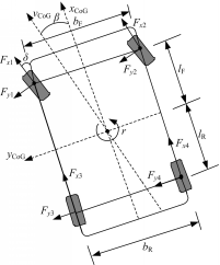
图1为前轮转向的车辆,假设汽车行驶过程中质心位置不发生变化,在车辆质心处建立坐标系,车辆前进的方向为x轴的正方向,水平向左的方向为y轴的正方向,垂直xy轴所在平面竖直向上为z轴的正方向,在定义坐标轴及正方向后,相应的力和力矩方向由右手螺旋定则确定。假设车辆在运行过程中满足以下条件:

(1)汽车在平直的路面上行驶,即忽略路面的坡度和倾斜度。

(2)汽车只受轮胎路面之间的摩擦力作用,即忽略侧向风和空气阻力对汽车的影响。

(3)忽略汽车侧倾运动及悬架动态的影响。

图1 车辆系统示意图Fig.1 Schematic diagram of vehicle system

根据牛顿第二定律和刚体动力学知识[ 13],车辆纵向、侧向运动可描述为

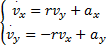(1)

式中:vx、vy为车辆的纵向速度和侧向速度;r为汽车的横摆角速度;ax、ay分别为车辆的纵向加速度和侧向加速度,表示为

ax=(Fx1+Fx2) cosδ-(Fy1+Fy2) sinδ+Fx3+Fx4

ay=(Fx1+Fx2) sinδ+

(Fy1+Fy2) cosδ+Fx3+Fx4

式中:Fxi、Fyi(i=1,2,3,4)分别为各轮胎所受的纵向力和侧向力。

采用数据/机理混合模型进行描述。作用在轮胎上的Fxi、Fyi与轮胎的垂直载荷Fzi以及路面附着系数μHi存在如下关系[ 4]:

Fxi(Fzi,Sxi,αi,μHi)=Fziμx(Sxi,αi,μHi) (2 a)

Fyi(Fzi,Syi,αi,μHi)=Fziμy(Syi,αi,μHi) (2 b)

式中:Sxi为轮胎的纵向滑移率;Syi为轮胎的侧向滑移率;Fzi受纵向加速度、侧向加速度、侧倾以及俯仰等的影响。

轮胎负载的转移包括静态转移、俯仰转移以及侧倾转移三部分,由于侧倾运动对垂直载荷的影响较小,所以将其忽略。因此,每个轮胎的垂直载荷可描述如下:

Fz1= - +

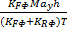
Fz2= - -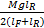

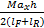
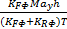
Fz3= + +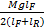

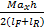
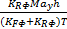
Fz4= + -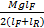

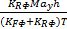
在式(2)中,αi(i=1,2,3,4)为各轮胎的侧偏角。它表示轮胎前进方向与轮胎实际行驶方向的夹角,是描述轮胎侧向动态特性的主要变量。每个轮胎的侧偏角可通过如下公式计算[ 14]:

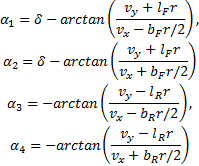
式中:δ为前轮转角。

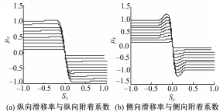
式(2)中,纵向、侧向轮胎/路面附着系数可以表示为轮胎的纵向滑移率、轮胎侧偏角以及最大路面附着系数的函数。由于这四者之间的关系较为复杂,采用数学机理建模较为困难,所以本文采用数据图表进行描述。在轮胎侧偏角αi为零,最大路面附着系数μHi在0.1~1变化时,轮胎纵向滑移率和轮胎/路面附着系数及轮胎侧向滑移率与轮胎路面附着系数之间的关系可由如图2所示的数据图表表示[ 15]。

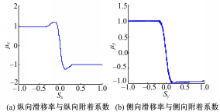
图2 α i=0时滑移率与附着系数的关系Fig.2 Relationship between slip rate and friction coefficient at α i=0

在μHi=1固定不变,轮胎的侧偏角在0°~5°之间每隔0.5°变化时,纵、侧向滑移率和纵、侧向轮胎/路面附着系数之间的关系可由图3所示的数据图表描述。不仅如此,当μH在[0 1]范围内取某一固定值时,相应地也可以得到轮胎侧偏角在0°~5°之间变化时轮胎滑移率与地面附着系数之间的数据描述。

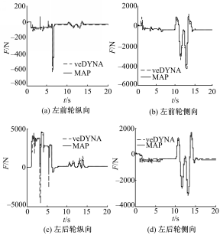
图3 μ Hi=1时滑移率与附着系数的关系Fig.3 Relationship between slip rate and friction coefficient at μ Hi=1

在得到轮胎滑移率与地面附着系数之间的关系后,将其代入式(2)中,结合式(1)描述的各轮胎的垂直载荷,就可以计算轮胎纵向力和侧向力。为验证采用数据/机理混合方法得到的轮胎力的准确性,在车辆运行的双移线工况,对由数据/机理混合描述的轮胎力进行验证,并与veDYNA中的轮胎力进行比较,其结果如图4所示。其中实线表示由式(2)得到的数据/机理混合描述的轮胎力,虚线表示用veDYNA中的轮胎模型得到的轮胎力。由于篇幅有限,这里只给出左前轮和左后轮的纵向、侧向轮胎力的验证结果。从图4中可以看出,由数据/机理混合描述的轮胎力与veDYNA中的轮胎模型得到的轮胎力存在较小的偏差,此偏差由两部分组成,一部分为数据图表描述的路面附着系数与实际附着系数之间的偏差,另一部分为车辆垂直载荷建模时引起的模型偏差。整体来说,采用数据/机理模型描述的轮胎模型其精度可以满足车辆速度估计的精度要求。

图4 数据/机理轮胎模型的轮胎力验证Fig.4 Tyre force verification of data/physics tire model

2 模块化级联车速观测器设计

通过式(1)的动力学描述可知,车辆的纵向、侧向速度通过横摆运动耦合在一起,但是由于车辆行驶时横摆角速度较小,同时侧向加速度也较小,由二者引起的科氏加速度rvy与纵向加速度ay相比对纵向运动影响较小,因此可以忽略科氏加速度对纵向速度的影响,相应的车辆动力学描述变为

(3)

经过以上简化,去除了侧向车速与纵向车速之间的耦合,因此可分别设计纵向车速观测器和侧向车速观测器,即采用模块化估计策略分别估计纵向车速和侧向车速。整个模块化车速观测器结构如图5所示。从图5可以看出,首先设计纵向车速观测器,然后将纵向车速的估计值作为侧向车速观测器的输入,因此纵向车速观测器和侧向车速观测器构成了级联结构。

图5 模块化车速观测器结构Fig.5 Structure of modular vehicle velocity observer

车辆正常行驶时,任意一个轮胎i的轮心运动速度在车辆坐标系x轴方向的分量vi,x可以表示为

vi,x=R dynωi cosδi(4)

式中:δi(i=1,2,3,4)为轮胎转角,R dyn为轮胎的有效半径。

根据vi,x与整车速度之间的关系,可得纵向车速vx粗略的测量值

vx,i:vx,i=R dynωi cosδi±rbi(5)

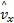
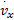
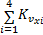
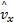
选取vx,i与纵向车速的估计值 的差值作为纵向车速估计的校正项,设计如下的车辆纵向速度观测器:

=ax+ (vx,i- )(6)

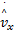
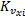
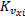
式中:纵向车速观测器的初始估计为 =ax; 为纵向车速观测器增益,设其为分段连续且有界,即 ≥kx>0,它反映了vx,i与 的一致程度。

将纵向车速的估计值作为已知量输入到侧向车速观测器中,同时利用侧向加速度ay与数据/机理混合轮胎模型的计算值之间的偏差作为校正项,构造侧向车速观测器

=- +ay+Ky(ay- )(7)

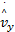
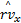
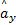
由于利用车身侧向加速度可计算得到车身的侧向受力may=fy(vx,vy,p),p=[ωi,δi]为车辆系统的输入。为分析方便,对侧向车速观测器进行如下变化:

=- +ay+

Ky(fy(vx,vy,p)-fy( , ,p))(8)

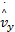
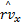
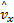
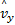
式中:Ky为可调的观测器增益,适当地选择Ky可使侧向速度估计误差减小。

根据ISS理论,在外部输入为零时,系统是渐近稳定的,对于有界的外部输入,系统的状态是稳定的[ 16]。根据文献[17]的分析可知,以幅值有界的科氏加速度rvy和道路坡度作为叠加输入,若纵向车速估计误差系统满足:

≤ + ( )(9)

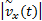
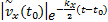
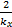
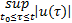
则纵向车速估计误差系统是ISS的。同时可以证明以纵向车速估计误差为输入,在侧向车速观测器增益满足:

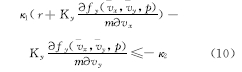
侧向车速估计误差系统是ISS的。在保证纵向车速观测器和侧向车速观测器各自稳定性的同时,以科氏加速度rvy和纵向车速粗略测量值与真实值之间的偏差作为输入的级联车速观测器是输入-状态稳定的。这使得整个级联车速观测器的稳定性得到有效保证。

3 非线性级联车速观测器增益选取
3.1 侧向车速观测器增益计算

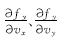
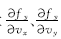
由以上对侧向车速估计偏差系统的分析可知,侧向车速观测器增益需满足式(10)(为书写简便,将 分别记做 由于 是变化的,导致 也是变化的。根据多胞型模型可知,如果 在一个有 个顶点的多面体中,可表示为

式中:m为已知常数,表示多面体的顶点;Co为由顶点组成的多面体的凸壳。

由于 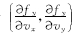在多面体中变化,所以存在常数β1,β2,…,βm使得 式中: βi=1。

由于式(11)中变化的 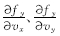采用多胞型模型进行描述,所以有下面的结论成立。

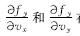
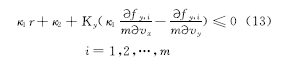
定理1 如果 在由式(11)表示的多面体内变化,并且满足式(12),那么,满足下面LMIs的任何时不变的Ky

均满足式(10)。

证明 由于 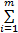βi=1,式(13)可以表示为 由式(12)可知,式(10)成立。至此,定理1证明完毕。

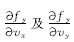
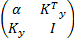
在式(13)中, 的各个分量已知并且是有界的,同时参数κ1和κ2也是有界的,因此,总可以找到侧向车速观测器增益Ky满足式(13)中的LMIs,因此式(13)总是成立的。为了有效抑制外部噪声对观测器造成的干扰,同时为了减小估计静差,可通过求解下面的优化问题来得到尽可能小的观测器增益Ky, α使得式(13)成立,同时满足

≥0(14)

3.2 基于随机算法的观测器参数及增益选取

由式(9)可知,对于幅值有界的叠加干扰,kx>0可保证纵向车速估计误差系统是ISS的,同时,纵向车速估计误差以kx/2的速度衰减,增大kx可加快估计偏差的衰减速度,但是kx过大会引起估计偏差系统振荡,因此需要选取合适的纵向车速观测器增益。另外,式(13)中,κ1>0、κ2>0是待确定的侧向车速观测器参数。在κ1、κ2确定后,可通过式(14)计算得到侧向车速观测器增益。下面采用随机算法理论通过蒙特卡罗实验讨论纵向和侧向车速观测器增益及参数的选取。由于级联观测器设计时,依次设计了纵向车速观测器和侧向车速观测器,因此在讨论观测器增益及参数选取时,也遵循这一原则,先讨论纵向车速观测器增益选取,然后确定侧向车速观测器的参数选取范围。主要步骤如下:

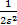
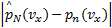
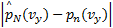
(1)根据单边Chernoff界确定随机采样点的数量。选取常数ε∈(0,1), ∈(0,1),如果N≥ log ,那么,对于概率大于1-δ,有 ≤ε(对于侧向车速观测器为: ≤ε)。因此,选取随机采样点N= log 。

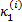
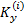
(2)采用线性同余发生器在(a1,b1)内产生均匀分布的纵向车速观测器增益 ,其中,a1、b1为待选择的常数。对于侧向车速观测器,在(a2,b2)及(a3,b3)内产生均匀分布的侧向车速观测器参数( , ),并由式(14)计算得到侧向车速观测器增益 。其中,a2、b2、a3、b3为待选择的常数。

(3)选择纵向车速估计的均值和方差为性能指标,即

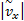
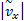
J(E( ))≤γ1,J(D( ))≤γ2(15)

并以此定义车速观测器增益的“好”集与“坏”集: =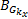

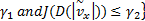
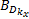
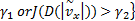
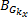
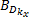
(16 a)

=

(16 b)式中:E(·)表示均值;D(·)表示方差; 为“好”集; 为“坏”集;γ1、γ2为待选常数。

相应地,以侧向车速估计的均值和方差为性能指标,并定义侧向车速观测器参数的“好”集与“坏”集: =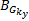

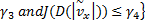
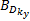
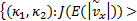
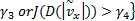
(17 a)

=

(17 b) 根据选定的性能指标及相应的“好”集与“坏”集,通过蒙特卡罗实验,确定纵向(或侧向)车速观测器增益(或参数)的选取范围。

4 仿真结果
4.1 车速观测器增益及参数选取

在车辆运行的常规和极限两种工况下对车速观测器增益及参数进行了仿真研究:①常规工况:车辆运行的目标车速为70 km/h,路面附着系数为0.9,超车并线操作。②极限工况:双移线工况,车辆运行的目标速度为70 km/h,路面附着系数为0.4,超车并线操作。

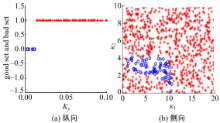
在常规工况的情况下对车速观测器参数及增益进行选取时,首先选取ε=0.05, 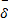=0.001,由单边Chernoff界确定随机采样点的数量为 N=1600,选取性能水平为γ1=0.15,γ2=0.6,通过蒙特卡罗实验确定纵向车速观测器增益选取范围,其中前800个采样点的结果如图6(a)所示。图中“o”代表“好”集中的纵向车速观测器增益的采样点,“*”代表“坏”集中的纵向车速观测器增益的采样点。在纵向车速观测器增益Kx=0.01时,选取性能水平γ3=0.02,γ4=0.1,对于每个随机采样点,通过式(14)计算得到侧向车速观测器增益,利用蒙特卡罗实验确定式(10)中满足性能指标要求的参数κ1、κ2的取值范围,其中前800个采样点的实验结果如图6(b)所示。图中“o”代表“好“集中侧向车速观测器参数的采样点,“*”代表“坏“集中侧向车速观测器参数的采样点。

图6 常规工况下观测器参数及增益选取Fig.6 Observer parameters and gain selection in conventional condition

在极限工况下对非线性级联车速观测器参数及增益进行选取时,选择纵向车速观测器增益的性能水平为γ1=0.35,γ2=0.5,其余参数与常规工况相同,通过实验确定纵向车速观测器的取值范围,其结果如图7(a)所示。在选定纵向车速观测器增益为Kx=0.01时,选取性能水平γ3=0.05,γ4=0.3,在其余参数与常规工况相同的情况下,通过蒙特卡罗实验确定侧向车速观测器的参数选取范围。其结果如图7(b)所示:

图7 极限工况下观测器参数及增益选取Fig.7 Observer parameters and gain selection in critical condition

从图6和图7可以看出,与常规工况相比,极限工况下观测器参数及增益的选取范围有所减小。主要是由于在不同的路面附着系数情况下,车辆的横摆角速度是不同的。极限工况下,在进行双移线操作时,车辆的横摆运动较为激烈,从而使得式(5)和式(13)中r值较大,因而限制了车速观测器增益和参数的选取范围。

4.2 估计结果比较

为了验证通过随机算法选取的级联车速观测器增益及参数对车辆速度估计的效果以及采用模块化级联车辆速度估计算法的准确性,将估计结果与车辆动力学软件veDYNA的运行结果进行了对比研究。由于车辆动力学软件veDYNA在建模时不仅考虑了轮胎和车体的动力学特性,同时还考虑了悬架、发动机、传动系的动力学特性以及路面环境对车辆运行状况的影响,因此,可以较为真实地反映车辆的实际运行情况。基于此,在采用随机算法确定车速观测器增益的基础上,分别在常规工况和极限工况下对级联车速观测器的估计效果进行仿真验证,轿车车辆参数如下:整车质量 m=1296 kg,质心到前轴的距离 lF=1.25 m,质心到后轴的距离 lR=1.32 m,前轮轮距 bF=1.424 m,后轮轮距 bR=1.399 m。为了验证本文所提出的非线性级联车速观测器的效果,将基于数据/机理模型的模块化车速观测器方法与单纯基于机理模型的非线性降阶车速观测器方法[ 18]进行了对比研究。

4.2.1 常规工况仿真结果

根据4.1节的车速观测器增益及参数选取结果,在图6(a)所示的“好”集中选取纵向车速观测器增益为Kx=0.01,同时在图7(b)所示的“好”集中选取参数κ1=5,κ2=3.5,通过求解式(10)确定侧向车速观测器增益Ky=0.017。下面在4.1节的常规工况下对级联车速观测器的估计结果进行仿真验证。其估计结果如图8所示。图中“CO”代表级联观测器估计结果,“ROO”代表降阶观测器估计结果,“veDYNA”代表veDYNA中车辆模型运行结果。从估计结果可以看出,用非线性级联观测器方法得到的车辆速度估计值与“veDYNA”中车辆运行结果相比偏差较小,说明级联车速观测器的校正项对车辆纵向速度和侧向速度的估计起到了调节作用,另外也说明采用随机算法得到的观测器增益是正确的。它使得车辆速度的估计值能够尽快收敛到由“veDYNA”提供的车速真值。与降阶车速观测器方法相比,本文给出的级联车速观测器方法的估计偏差略大于非线性降阶观测器方法,主要是由于轮胎力采用数据实现时存在一定的模型偏差,另外,纵向车速动力学中忽略的科氏加速度也在一定程度上引起了纵向速度估计的偏差,因此使得估计精度略有降低,但总体可满足性能指标的要求。

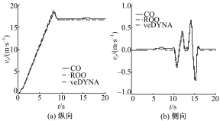图8 μ=0 .9时双移线工况估计结果(常规工况)Fig.8 The estimation results in double line change condition at μ=0.9(conventional condition)

4.2.2 极限工况仿真结果

为更充分说明非线性级联观测器方法的有效性,在4.1节的极限工况下进行了仿真研究。观测器参数及增益选取与常规工况相同。在这种工况下车辆速度的估计结果如图9所示。

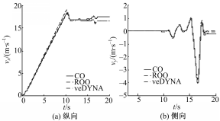图9 μ=0.9时双移线工况估计结果(极限工况)Fig.9 The estimation results in double line change condition at μ=0.4(critical condition)

极限工况下的仿真结果除了可以得到与常规工况相同的结论外,从极限工况仿真图形还可以看出,纵向车速观测器的估计偏差有所增加,主要是由于极限工况下,车辆的横摆运动和侧向速度都有所增加,导致被忽略的科氏加速度对纵向车速估计结果的影响有所增加。另外,由于车辆转向系统、动力传动系统以及液压制动系统均为机械系统,使得车辆在进行转向操作以及加减速时横摆角速度、纵向加速度和侧向加速度存在一定的延时,在极限工况时必然引起估计误差的增加。此外,从纵向车速偏差系统的稳定性分析可以看出,科氏加速度作为纵向车速观测器的叠加输入,在其不为零的情况下必然导致级联车速观测器在稳态时存在一定的偏差。而侧向车速估计误差系统是以纵向车速估计的偏差作为输入的,这就会使得侧向车速估计误差会有所增加,但是由文献[17]的稳定性分析知,侧向车速是ISS的,即在外部有界输入时,估计误差是有界的。图9所示的极限工况的仿真结果也很好地验证了这一点。同时,基于随机算法选取的观测器参数及增益除从理论上给出观测器增益的具体取值以外,还可有效保证得到较小的车速估计误差。

为了对级联车速观测器方法的计算速度进行验证,采用xPC-Target实时仿真环境和dSPACE硬件系统对其实时性进行实验研究,并与非线性降阶车速观测器方法进行了对比。在实验时,车辆动力学软件运行于xPC-Target的目标机中,车辆速度观测器实时运行于dSPACE硬件系统中。经计算可知,非线性级联车速观测器在一个采样周期内的计算时间为0.286 ms,而非线性降阶车速观测器在一个采样周期内的计算时间为0.367 ms。说明级联车速观测器与降阶车速观测器相比,计算时间缩短了约22%。因此,本文采用的数据/机理混合模型设计的车辆速度观测器可有效提高观测器的计算速度,从而可进一步为车辆速度观测器的实车应用奠定基础。

5 结束语

采用数据和机理模型相结合的方式建立了轮胎模型,进一步得到了车辆动力学描述并进行了模型验证。该模型可克服复杂轮胎模型带来的运算负担。在此基础上,采用模块化估计策略,设计了非线性级联车速观测器,在保证级联车速观测器ISS的基础上,应用随机算法讨论了车速观测器参数及增益的选取问题,确定了级联车速观测器增益及参数的选取范围。通过常规和极限工况下的仿真研究表明,基于随机算法通过数据/机理混合模型设计的级联车速观测器,在车辆进入极限工况以后,纵向车速观测器的估计偏差有所增大,但总体可以满足要求。同时,通过实时性研究说明采用数据/机理混合的车辆动力学模型可有效提高观测器的计算速度,进一步为实车应用奠定基础。

The authors have declared that no competing interests exist.

参考文献
[1] Sobhan P V S, Kumar G V N, Priya M R, et al. Look up table based fuzzy logic controller for unmanned autonomous underwater vehicle[C]∥International Conference on Advances in Computing, Control, and Telecommunication Technologies. Trivan-drum, Kerala: IEEE, 2009. [本文引用:1]
[2] 黄海燕. 汽车发动机试验学教程[M]. 北京: 清华大学出版社, 2009. [本文引用:1]
[3] Gao B, Chen H, Zhao H, et al. A reduced-order nonlinear clutch pressure observer for automatic transmission using ISS[C]∥The 47th IEEE Conference on, Shanghai, China, 2008. [本文引用:1]
[4] Tjonnas J, Johansen T A. Stabilization of automotive vehicles using active steering and adaptive brake control allocation[J]. Control Systems Technology, IEEE Transactions on, 2010, 18(3): 545-558. [本文引用:2] [JCR: 2.0]
[5] Tanelli M, Astolfi A, Savaresi S M. Robust nonlinear output feedback control for brake by wire control systems[J]. Automatica, 2008, 44(4): 1078-1087. [本文引用:1] [JCR: 2.919]
[6] Kayacan E, Oniz Y. A grey system modeling approach for sliding-mode control of antilock braking system[J]. Industrial Electronics, IEEE Transactions on, 2009, 56(8): 3244-3252. [本文引用:1] [JCR: 5.165]
[7] Daily R, Bevly D M. The use of GPS for vehicle stability control systems[J]. Industrial Electronics, IEEE Transactions on, 2004, 51(2): 270-277. [本文引用:1] [JCR: 5.165]
[8] Pistoia G. Vehicle applications: traction and control systems[J]. Battery Operated Devices and Systems, 2009: 321-378. [本文引用:1]
[9] Grip H F, Imsland L, Johansen T A, et al. Nonlinear vehicle side-slip estimation with friction adaptation[J]. Automatica, 2008, 44(3): 611-622. [本文引用:1] [JCR: 2.919]
[10] Zhao L H, Liu Z Y, Chen H. Design of a nonlinear observer for vehicle velocity estimation and experiments[J]. Control Systems Technology, IEEE Transactions on, 2011, 19(3): 664-672. [本文引用:1] [JCR: 2.0]
[11] Piccoli B, Zadarnowska K, Gaeta M. Stochastic algorithms for robustness of control performances[J]. Automatica, 2009, 45(6): 1407-1414. [本文引用:1] [JCR: 2.919]
[12] Jelali M. An overview of control performance assessment technology and industrial applications[J]. Control Engineering Practice, 2006, 14(5): 441-466. [本文引用:1] [JCR: 1.669]
[13] Pacejka H. Tyre and Vehicle Dynamics[M]. Burlington: Elsevier, 2005. [本文引用:1]
[14] Kienche U, Nielsen L. Automative Control System[M]. Berlin: Springer, 2000. [本文引用:1]
[15] Kim J. Identification of lateral tyre force dynamics using an extended Kalman filter from experimental road test data[J]. Control Engineering Practice, 2009, 17(3): 357-367. [本文引用:1] [JCR: 1.669]
[16] Sontag E D. Input to State Stability: Basic Concepts and Results. in Lecture Notes in Mathematics[M]. Berlin: Springer-Verlag, 2005. [本文引用:1]
[17] 郭洪艳, 陈虹, 张华玉. 车辆动力学数据/机理建模及车速估计应用[C]∥第30届中国控制会议, 烟台, 2011. [本文引用:1]
[18] 郭洪艳. 车辆速度估计非线性观测器方法研究[D]. 长春: 吉林大学通信工程学院, 2010.
Guo Hong-yan. Study on nonlinear observer method for vehicle velocity estimation[D]. Changchun: College of Communication Engineering, Jilin University, 2010. [本文引用:1]