何忠政(1986),男,博士研究生.研究方向:可信计算,移动计算.E-mail:hezhongzheng@hrbeu.edu.cn
针对实时系统容错模型只能容忍任务执行时一次故障发生的缺陷,基于卷回恢复容错模型,提出了任务局部最优检查点间隔求解算法,使实时系统任务能够容忍任务执行过程中多次故障的发生;进而基于局部最优检查点间隔提出任务集检查点间隔全局优化(CIGO)策略。基于不同的检查点间隔优化机制,结合实时系统任务最坏响应时间的计算公式进行系统可调度性分析。仿真实验表明,与局部最优检查点间隔相比,基于全局优化检查点间隔的实时系统容错能力有显著提升。
To overcome the defect of the real-time system fault-tolerant model that could only tolerate one fault occurred during the task execution process, a task Local Optimum Checkpoint Interval (LOCI) iterative algorithm was proposed. The algorithm is based on the checkpoint and rollback recovery fault tolerant model to make the task of the real-time system could tolerate multiple faults occurred during the task execution process. Then the Checkpoint Interval Global Optimization (CIGO) algorithm of the task set was proposed. The schedulability of the real-time system was analyzed based on the different checkpoint interval optimization mechanisms according to the calculation formula of the task worst case response time. The simulation results show that the strategy based on the GIGI can significantly improve the system fault resilience compared to that based on the LOCI.
实时系统的任务必须按时、可靠地执行完成,否则将导致灾难性后果[ 1]。实时系统中电路晶体管尺寸及工作电压的减小降低了电路噪声容限,而且集成度的提高也使芯片更易受瞬时故障影响。由瞬时故障所导致的计算机可靠性已成为一个严峻的问题[ 2, 3, 4]。外界环境也可能导致晶体管PN结内部逻辑状态发生改变[ 5]。因此瞬时故障容错技术对保证系统的可靠性至关重要。
为了确保系统实时性和可靠性,需对任务进行可调度性分析[ 6]。基于卷回恢复容错模型进行任务调度,能够在瞬时故障多次发生情况下,将任务恢复至过去某一正确状态,避免任务重新执行所带来的时间浪费。局部最优检查点间隔能够在提供容错能力的同时,最小化任务额外执行时间。检查点间隔全局优化能够调整故障恢复开销,以充分利用其他任务的空闲时间。文献[7]中卷回恢复容错模型的检查点间隔是单次故障情况下的最优检查点间隔,该检查点间隔并不是整个任务集的最优检查点间隔。文献[8]中可调度性分析模型的故障发生次数是确定的,而任务故障次数是由任务响应时间和故障发生间隔决定的。基于上述问题本文首先基于文献[8]的卷回恢复容错模型,对文献[7]的任务最坏响应时间计算公式进行改进。然后基于文献[8]的容错模型,提出了多次瞬时故障发生时的局部最优检查点间隔求解算法。接着通过最坏响应时间计算公式的分析,提出了检查点间隔全局优化(CIGO)策略。最后通过仿真实验比较了不同检查点间隔优化机制下系统的容错能力。
实时系统的任务集可表示为 Γ={ τ1, τ2,…, τ n}, τ i表示实时系统执行的周期性任务。在卷回恢复容错模型下,任务 τ i的配置属性可由七元组
在任务 τ i到达后,系统采用固定优先级调度算法(如速率单调算法(Rate-Monotonic,RM)[ 9])为其分配一个固定且唯一的优先级 p i∈{1,2,…, n}。由 p i可确定任务集 Γ的两个子集:优先级高于 p i的任务集合 hp( i)( hp( i) ={ τ j∈ Γ|p j >p i})和优先级不低于 p i的任务集合 hpe( i)( hpe( i) =hp( i)∪{ τ i})。任务集 Γ中任务的优先级 p i数值越大,则其优先级越高。本文的研究基于以下条件:
(1)仅进行单处理器系统中瞬时故障的容错处理,且瞬时故障在故障检测阶段能够被成功检测;
(2)任务之间相互独立,无故障传播,且无资源共享导致的任务阻塞;
(3)检查点间隔是相等的;
(4)两个连续发生的故障之间存在最小时间间隔,记为 TE。若故障发生间隔小于 TE,则系统不可调度;系统能够容忍的 TE越小,则其容错能力越强。
文献[7]推导出了卷回恢复容错模型下实时系统任务 τ i的最坏响应时间 R i的计算公式。任务最坏响应时间为任务自身的最坏执行时间、优先级比该任务高的任务的抢占执行时间和故障后的卷回恢复时间三者之和[ 7]。卷回恢复时间为任务最坏响应时间内可能发生的故障次数和最大故障恢复开销的乘积。该方法将故障检测开销和检查点设置开销合二为一,表示为 O i,且忽略故障恢复开销;而故障的检测、恢复及检查点设置是实现容错必需的过程,且对于不同的任务这三者的开销各不相同,即使相同任务在不同的时间和负载条件下运行时,三者的开销也是不同的。其任务被检查点分成的段数 m i是在任务只发生一次故障的情况下求得的,而在实际情况下任务发生多次故障是极有可能的。文献[7]中 R i( TE)的计算公式为
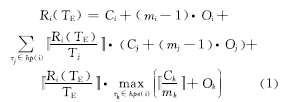
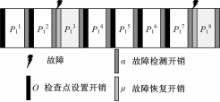
图1为基于卷回恢复技术的容错模型[ 8],该模型为 n i =6且发生故障次数 k=2时的执行情况。故障在任务 P1的第2个和第6个检查点间隔的故障检测阶段被检测出来。基于该模型,对公式(1)进行扩展,在任务可能发生多次故障的情况下,考虑检查点设置开销、故障检测开销、故障恢复开销,得到任务 τ i的最坏响应时间计算公式如式(2)所示:
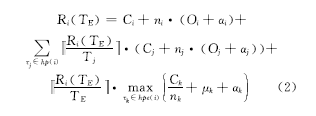
检查点的设置给任务执行带来了一定的额外开销,这主要包括无故障时的检查点设置开销和故障后的卷回恢复开销;故障检测也为正常运行的任务带来了额外开销。检查点卷回恢复的开销由检查点间隔决定,因此检查点间隔对于容错实时系统任务的可调度性有重要影响。不同配置的任务其故障发生次数是不相同的;相同的任务在不同的故障间隔 TE下,故障发生次数也不相同,局部最优检查点数量也不同,因此其最坏响应时间 R i也不同。 R i可表示为局部最优检查点数量 nlocal i和故障发生次数 k的函数。文献[8]提出了任务独自执行情况下发生 k次故障时的响应时间计算公式(式(3)),并求解了该公式下任务局部最优检查点间隔的计算公式(式(4))。
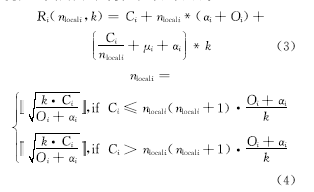
任务执行过程中所发生的故障次数是由任务的最坏响应时间及系统的故障发生间隔 TE决定的。在 TE小于最坏响应时间时,任务可能会发生多次瞬时故障;但只要故障发生间隔 TE满足大于ma 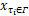
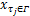

算法从任务的最坏执行时间 C i开始,按照公式(3)(4)迭代求解任务故障发生次数 k和局部最优检查点数量 nlocal i,最后算法收敛于唯一的故障发生次数 k,由 k得局部最优检查点数量 nlocal i。
算法收敛性证明:随着迭代次数的增加,故障发生次数 k增加,检查点数量 nlocal i增加,故障恢复间隔 C i /nlocal i减小。相邻 k值间 R i( nlocal i, k)的增量计算公式为: Δ=R i( nlocal i, k+1, k+1) -R i( nlocal i, k, k)。将 nlocal i, k+1 = 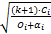
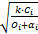
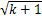
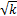
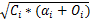
在考虑故障检测、故障恢复和检查点设置开销且任务只发生一次故障的情况下,基于文献[7]方法的任务最优检查点间隔计算公式为
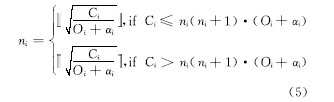
表1为在任务只发生一次故障情况下求得不同 TE下的任务最坏响应时间,其检查点数量根据检查点间隔计算公式(5)求得;表2为在局部最优检查点间隔情况下求得的任务最坏响应时间。比较两表发现,基于一次故障情况下的检查点间隔时,任务在 TE =61时是不可调度的;而在局部最优检查点间隔 <10,14,24 >时,任务在 TE =26时是不可调度的。因此基于局部最优检查点间隔的任务可调度性优于基于一次故障情况下检查点间隔的任务可调度性。
| 表1 基于一次故障情况下检查点间隔的任务最坏响应时间 Table 1 the task worst case response time based on the checkpoint interval under the single fault |
| 表2 基于局部最优检查点间隔的任务最坏响应时间 Table 2 The task worst case response time based on the local optimum checkpoint interval |
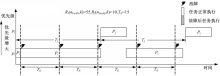
局部最优检查点间隔是仅仅考虑任务独自执行时的最优检查点间隔。当存在优先级关系的多个任务并发执行时,高优先级的任务会周期性抢占低优先级任务的执行,因此每个任务的最坏响应时间较单独执行时的响应时间会有所变化,任务的故障发生次数也会有所变化。如图2所示:
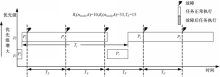
由于任务 P j的周期性抢占,使任务 P i的故障发生次数增加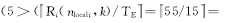 4))。如图3所示:
4))。如图3所示:
由于任务 P j的周期性抢占,使任务 P i的故障发生次数减少 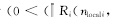
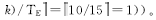
在卷回恢复容错实时调度下,全局优化检查点间隔配置 nglobal =
对于不可调度任务 τ i,定义最大故障恢复开销任务集合max D( i) ={ τ j∈ Γ|τ j∈ hpe( i)∧( C j /nglobal j +μ j +α j) =ma 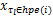
IncChekptSet( nglobal, i) =
{ τ j∈ Γ|τ j∈max D( i)∧
R j( nglobal, T e( nglobal) -1)
对于不可调度任务 τ i,非最大故障恢复开销任务集合 Nmax D( i) ={ τ j∈ Γ|τ j∈ hpe( i)∧( C j /nglobal j +μ j +α j) <ma 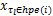
DecChekptSet( nglobal, i) ={ τ j∈ Γ|τ j∈
Nmax D( i)∧ R j( nglobal,T e(nglobal)-1)
( C j /nglobal j+μ j+α j)< 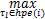
检查点间隔全局优化( CIGO)算法的伪代码如下所示。
(1) 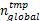
(2) T E← T e( 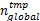
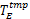
(3) while TRUE
(4) n local← ChekptLN( T E)
(5) n global← n local
(6) if(∀ τ i∈ Γ: R i( n global, T E)
(7) 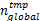
(8) 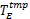
(9) T E← T E←1
(10) if( T E≤ ma 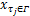
(11) if( T E≤ ma 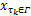
(12) else
(13)∀ τ i∈ D( n global)
(14) if(( IncChekptSet( n global, i) =⌀) &&( DecChekptSet( n global, i) =⌀)) exit while
(15) if( IncChekptSelt( n global, i)≠⌀)
(16) n global← ma 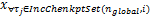
(17) if( |IncChenkptSet( n global, i) |=1) T E← min( T e( n global), T E)
(18) if( DecChekptSet( n global, i)≠⌀)
(19) n global← mi 
(20) if( |DecChekptSet( n global, i) |=1) T e← min( T E( n global), T E)
(21) end if
(22) end while
(23) n global← 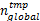
(24) T E← 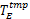
CIGO算法确定系统中不可调度的任务后,根据上述讨论对任务的全局检查点间隔进行配置,得到全局优化检查点间隔 nglobal。对已经采用 FP( Γ)分配优先级的任务集 Γ,CIGO算法从其局部最优检查点间隔 nlocal及初始 TE开始迭代搜索全局优化检查点间隔 nglobal,其搜索过程分为两部分:
(1)验证部分:计算当前 TE下各任务的局部最优检查点间隔 nlocal并作为初始值赋给 nglobal,然后求解各任务在当前 nglobal时的最坏响应时间,并判断是否大于其截止时间来决定任务的可调度性。若系统可调度,则将当前 nglobal与 T E保存到 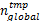
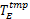
(2)搜索部分:若当前 nglobal与 TE下存在不可调度任务,则搜索新的全局优化检查点间隔。此时 D( nglobal)≠∅,对于 D( nglobal)中任意 τ i,依次增加IncChekptSet( nglobal, i)中各任务的检查点数量,并验证新 nglobal的有效性,将满足条件的最大检查点数量赋给新的全局优化检查点间隔,最后取新 nglobal下的 T e( nglobal)与当前 TE中的较小者作为新的 TE(见第16、17行);然后依次减小DecChekptSet( nglobal, i)中各任务的检查点数量,并验证新 nglobal的有效性,将满足条件的最小检查点数量赋给新的全局优化检查点间隔,最后取新 nglobal下的 T e( nglobal)与当前 TE中的较小者作为新的 TE(见第19-20行)。当条件 TE≤ma 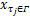
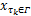
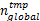
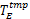
表3给出了实时周期性任务集 Γ={ τ1, τ2, τ3}在全局优化检查点间隔情况下容错调度结果。由表2知,在局部最优检查点间隔 <10,14,23 >下,当 TE =27时,各任务最坏响应时间均小于其截止时间,系统是可调度的。当 TE =26时,此时局部最优检查点间隔为 <10,14,24 >,任务 τ3最坏响应时间 R3(26)超过了其截止时间 D3,导致系统不可调度。由表3知在全局优化检查点间隔 <6,9,31 >下,当 T E =23时,系统是可调度的。当 TE =22时,在全局优化检查点间隔 <6,9,31 >下,任务 τ3最坏响应时间 R3(22)超过了其截止时间 D3,系统是不可调度的。在局部最优检查点间隔下,系统容错能力 T E为27;在全局优化检查点间隔下,系统容错能力 TE为23,容错能力提升(27-23)/27×100%=14.81%。因此在局部最优检查点间隔下并不能获得最优的系统可调度性,检查点间隔全局优化能够进一步提升系统可调度性。
| 表3 基于全局优化检查点间隔的任务最坏响应时间 Table 3 The task’s worst case response time based on the global optimization checkpoint interval |
为验证全局优化检查点间隔的高效性,本文用仿真试验模拟了810个任务集,每个任务集包含4个实时周期性任务(可扩展至包含任意数量任务的任务集)。试验计算机的配置为:Intel(R) E4500 CPU,2G内存,500G硬盘。参照文献[10]中的仿真方法,各任务的相关属性是随机产生的,但任务集 Γ中任务 τ i的配置需满足以下约束条件:
(1)任务 τ i的周期 T i和截止时间 D i服从区间[100,3000]上的均匀分布,且 D i≤ T i。
(2)任务 τ i的处理器利用率 U i =C i /T i服从均值为 U/4的指数分布,其中 U= 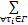
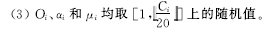
采用固定优先级调度算法RM对实时系统任务集 Γ进行卷回恢复容错实时调度。计算任务集 Γ分别在局部最优检查点间隔和全局优化检查点间隔下所能达到的最小故障发生间隔 LTE和 GTE。通过 ΔGLTE =100% *(( GTE -LTE) /LTE)来衡量检查点间隔全局优化算法相对于局部最优检查点间隔策略,系统容错能力的提升程度。
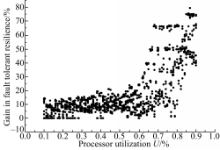
检查点间隔全局优化算法的系统容错能力提升情况如图4所示:
图4中横坐标表示任务集的处理器利用率 U,纵坐标表示系统容错能力的提升幅度 ΔGLTE,图中黑点表示一个任务集的 ΔGLTE值。由黑点的分布可知,当0
由于计算机设备自身及恶劣环境的影响,实时系统面临严峻的瞬时故障影响,导致系统中任务不能按时完成,甚至发生灾难性后果。因此针对实时系统瞬时故障卷回恢复容错模型只能容忍任务执行过程中一次故障发生的情况,本文对实时系统的容错调度进行研究,提出了任务局部最优检查点间隔迭代求解算法,使任务能够容忍执行过程中多次瞬时故障的发生;进而提出了任务集检查点间隔全局优化算法,并通过任务的最坏响应时间来分析系统的可调度性。由仿真实验中 ΔGLTE的变化情况可知,检查点间隔全局优化算法能够在局部最优检查点间隔策略的基础上进一步提升系统的容错能力。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|