刘敬猛(1967),男,副教授.研究方向:电机设计与控制,机器人技术.E-mail:jmliubuaa@126.com
为了提高三自由度永磁球形电机的运动性能、控制效率和减少控制成本,对具有三维位置检测功能的三自由度永磁球形电机的控制方法进行了研究。首先建立了三自由度永磁球形电机的磁场模型、动力学模型、力矩模型和反电动势模型,并分析其运动控制机理。在此基础上求解永磁球形电机的电压平衡方程和动力学方程,得到永磁球形电机的控制模型,并结合PID控制方法,提出了永磁球形电机的基于电压模型的PID闭环控制方法。仿真结果表明,提出的电压控制方法与传统的电流力矩控制法相比可以明显提高球形电机的运动性能。
In order to improve movement performance and control efficiency, and to save the cost of the control system of the three-DOF permanent magnet spherical motor, this paper studies a three-DOF permanent magnet spherical motor with three-dimensional position detection and its control method. The magnetic field model, the dynamic model, the torque model and the back-EMF model of permanent magnet spherical motor were established. The motion control mechanism was analyzed. Based on these models, the voltage balance equation and kinetic equation of the spherical motor were put forward and the control model was established. Applying the PID control method, the closed-loop control method of the spherical motor was obtained. Simulation results show that, compared with the current torque method, the control method proposed in this paper can greatly improve the movement performance.
随着现代科学技术的发展,多自由度运动装置的研究受到越来越多国内外学者的关注。但是,市场上所有的常规电机都只能产生单自由度旋转运动。为了产生多自由度旋转运动,必须将多个单轴电机以串联、并联或者是串并混联等方式实现。这种多电机组合的方式固然能实现多自由度旋转运动,但是它们存在一些难以克服的内在缺陷:传动机构弹性变形和运动死区造成的运动精度低,存在回程误差以及工作空间内存在奇异点等。为了更好地满足多自由度驱动装置的需求,研究者们提出了球形电机的概念,它可以在一个关节实现三自由度旋转运动,具有结构紧凑、工作空间内无奇异点、没有回程误差积累以及高动态响应性能等显著优点。球形电机有多种设计方案,永磁球形电机由于结构紧凑、无需励磁系统等优点在近些年备受关注[
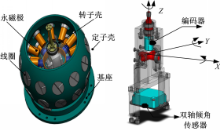
如图1所示:
球形电机由转子和球壳形定子组成。转子通过球关节连接于定子基座,且与定子的球心重合。转子上沿转子赤道面均匀分布有8个圆柱形永磁体,采用交替充磁策略。定子上沿定子赤道面上下对称分布有2层24个线圈,线圈轴线指向球心。线圈骨架采用空气芯结构,这样可以保证球形电机力矩模型的线性特点,大大简化了球形电机控制的复杂度。转子的姿态由固定于球关节的编码器和双轴倾角传感器组合测得(见图2):
其中,编码器测量转子自旋方向的运动,双轴倾角传感器测量转子倾斜方向的运动。球形电机的具体结构参数如下:定子壳内/外半径为100/117 mm;转子半径为56.5 mm;永磁极个数为8;圆柱永磁极参数为 r=10 mm, l=20 mm;线圈个数为24/2层;线圈匝数为1600;最大倾斜角度为±15°。
球形电机机械结构三维图如图3所示:
当给球形电机的定子线圈通电时,定子线圈和转子磁极之间产生力矩作用,推动球形电机的转子产生运动。当给所有的定子线圈通电时,转子可以绕它的转子轴旋转运动(即自旋运动);当给位于不同纵向位置的线圈通电时,转子可以绕不同方向倾斜运动。所以,当给不同的定子线圈通电时,转子可以产生空间三自由度的运动。球形电机工作原理如图4所示:
球形电机磁场研究是其理论研究的基础,本文提出了一种精确又实用的磁场解析分析方法。首先求解单个圆柱磁极产生的磁场,通过麦克斯韦方程组和其他的磁场特性方程,得到球形电机线圈及气隙区域的拉普拉斯方程[
如果 A是磁矢量,通过矢量定律和库伦定律,对于均匀永磁体,可以得到转子气隙区域和永磁体区域的拉普拉斯方程。将磁矢量 A表示在圆柱坐标系下:
A =( A r, A θ, A z),则∇2 A =0(1)
由于转子磁极为圆柱形,所以选择圆柱坐标系求解拉普拉斯方程:
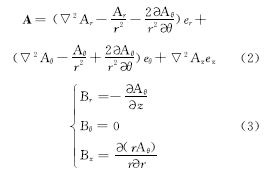
式中: r表示圆柱坐标系下沿 e r方向的坐标值。
根据不同的磁介质,磁场切向和法向边界条件特性如下:
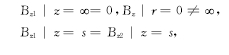

应用分离变量法和贝塞尔方程求解拉普拉斯方程可以得到:
B r =ae -kz J1( kr)(4)
B z =ae -kz J0( kr)(5)
圆柱磁极有 N极和 S极,并且设其磁荷密度分别为 B r和 -B r。按照等效磁荷原理和镜像原理,磁极轴线上 P点的磁场强度为
BP≈ 
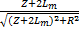

ae -kz J0(0) =
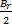

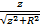
求解方程(7)可以求得参数 a和 k的确切值。
在单个圆柱磁极磁场的基础上,可以得到整个球形电机的磁场。首先,将圆柱坐标系转换为直角坐标系,得到在磁极直角坐标系下的磁场。然后,通过坐标变换求得在转子坐标系下的单个磁极的磁场分布。最后,通过矢量叠加原理,叠加所有磁极产生的磁场,求得整个球形电机的磁场分布。
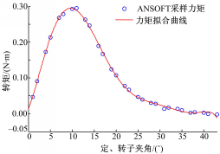
在建立三自由度直流永磁球形电机的控制模型中,力矩建模是重要的分析步骤。根据洛伦兹力可知,每个线圈产生的驱动力矩与线圈电流的大小成正比,将24路线圈的力矩进行叠加,即可得到24路电流值与输出力矩的关系。应用有限元软件 ANSOFT求解球形电机的力矩模型[
T i, j =f( ψ i, j) 
ψ i, j =cos -1
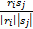 | (9) |
式中: ψ i, j为第 i个转子永磁体和第 j个定子线圈所成的夹角; f( ψ i, j)为力矩函数。
式(9)中 f( ψ i, j)为未知,用 ANSOFT软件对球形电机力矩进行仿真,用 MATLAB的函数逼近模块,可以得到连续的7次函数 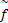
其中, 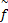

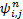
G i: G i =
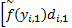 | (10) |
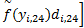
式中: d i, j为第 i个永磁体和第 j个定子线圈所成力矩的方向矢量。
根据叠加原理,将8个转子永磁体的力矩矩阵相加,可以得到全局的力矩矢量
G: G = 
将力矩矩阵右乘24路电流值列矢量 I i,就可以得到球形电机的力矩输出矢量 T: T = 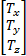
动力学模型描述了驱动力矩与球形电机转子运动状态的关系,其建模有效性直接影响控制系统的性能。为了方便数学建模,忽略摩擦力及外界干扰的影响。通过拉格朗日方程和欧拉角可以得出转子的动力学方程[
M( q) 
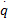
式中:电机的位置矢量为 q =
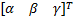 | (14) |
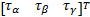
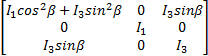
C( q,
 | (15) |
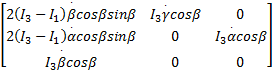
转动惯量通过用 SolidWorks软件求出。其中, I1 =1 .75 ×10 -3, I3 =1 .45 ×10 -3,单位是 kg· m2。
球形电机的反电动势模型是电压控制研究的基础。应用磁场有限元软件的瞬态磁场分析功能,可以分析电机、变压器等的反电动势特性[
e ij =n
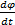 | (16) |
式中: n为线圈的匝数; φ为线圈中的磁通量。
直流电机的反电动势与转子的转速成正比例关系,同样三自由度球形电机的线圈的反电动势也与转子的转速成正比。不难发现,三自由度球形电机的单个磁极和线圈产生的反电动势除了与转子转速成正比外,还与转子和定子的相对位置及转子和定子轴线的夹角有关系:
e ij =Nf( θ ij)(17)
式中: N为转子的转速; f( θ ij)为球形电机反电动势关于转子和定子轴线的夹角的函数。
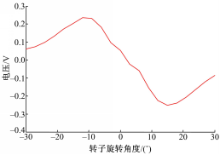
利用 ANSOFT仿真得到的球形电机不同位姿的反电动势数据如图6所示:
用最小二乘法拟合得到f(θij) = 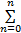

球形电机的电压平衡方程与直流电机的电压平衡方程类似,由于球形电机有多个线圈,所以它的电压平衡方程采用矩阵形式表达:
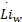
式中: UE = 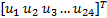
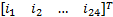
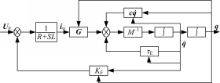
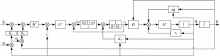
结合球形电机的动力学方程和电压平衡方程可得到球形电机的电压控制模型和控制方框图,如图7所示:
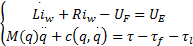 | (19) |
从球形电机电压控制方框图可以得出球形电机的控制模型与机器人操作臂的控制模型相似,所以应用于机器人操作臂的控制算法都可以应用于球形电机的控制。本文将PID控制方法应用于电压控制模型中,PD位置控制外环、PI电流控制内环。电流控制环可以减小线圈反电动势和电流变化对位置环的影响[
电机的位置和速度跟踪误差方程以及控制律如下:
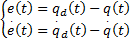 | (20) |
τEM =M
 | (21) |
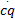
Kp =diag( kp1, kp2, kp3)(22)
Kv =diag( kv1, kv2, kv3)(23)
τEM =G iw(24)
控制算法的稳定性和实时性是电机动态特性良好的保证。在所有的仿真中,转子轨迹特性表示为欧拉角的形式(α,β,γ),并且在开始时间(t=0),期望的速度 
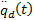
q d(t)=
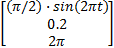 | (25) |
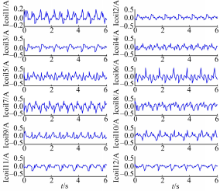
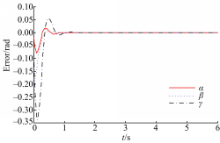
利用MATLAB软件仿真得到的基于电压模型的PID控制方法的响应曲线、线圈电压波形曲线、误差曲线分别如图9、图10、图11所示:
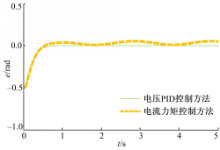
通过对比基于电压模型的PID控制方法和传统的电流力矩控制方法的阶跃信号响应曲线(见图12):
和误差曲线(见图13):
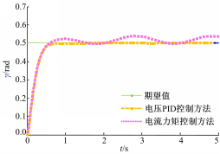
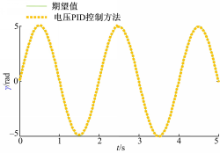
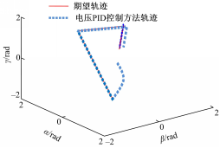
可以验证基于电压模型PID控制算法的优越性。正弦信号响应曲线(见图14):
和三维位置跟踪曲线(见图15),验证了基于电压模型PID控制算法的动态性能。
从仿真结果可以看出,对于电流力矩法,跟踪误差比较大,而基于电压模型的PID控制算法,由于初始位置位于原点,若期望轨迹不是以原点作为起点,则初始时刻需要调整输出值进行轨迹跟踪,达到调整时间后,轨迹的误差就很小了。从而可以得出结论,由于球型电机的建模不确定性,以及摩擦力和外部的干扰存在,使用传统的电流力矩法会产生很大的控制误差。而基于电压模型的PID控制算法,解决了建模不确定及摩擦和外界干扰的影响,降低了系统误差,并且,正弦和线性信号的响应曲线也证明了基于电压模型的PID控制方法的有效性。
对具有8个转子永磁体和24路定子线圈构成的三自由度永磁球形电机进行了基于电压模型的闭环控制研究。结合拉普拉斯方程和等效磁荷原理求解得到球形电机的磁场解析模型,运用ANSOFT及MATLAB软件建立了球形电机力矩模型和反电动势模型,利用XYZ欧拉角对球形电机运动机构进行了运动学分析。最后,结合球形电机的电压平衡方程和动力学方程得到球形电机的控制模型,并将PID控制方法应用于控制模型得到球形电机的基于电压模型的闭环控制方法。仿真结果证明了此种控制方法的有效性,为球形电机实现稳定精确的运动控制提供了理论基础。下一步,将基于本文提出的基于电压模型的控制算法开展实验研究,以求进一步验证理论的正确性和推动球形电机的工程应用研究。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|