胡立坤(1977),男,教授,博士.研究方向:非线性系统动力学及控制,可再生能源变换系统及应用.E-mail:hlk3email@163.com
First, the singularity problem is analyzed in the conventional fast terminal sliding mode controller when applied to six-axe harmonious motion control of the 6-DOF manipulator. Then, a non-singular fast terminal sliding mode controller is proposed, and the stability of the control system is proved using the Lyapunov theory. The non-singular fast terminal sliding mode controller is applied to six-axe harmonious motion control of the 6-DOF manipulator. The results illustrate that the non-singular fast terminal sliding mode method can improve the stability, accuracy, convergence speed and robustness of the position and orientation control of 6-DOF manipulator.
滑模控制之所以被广泛应用于机器人、电机等非线性的复杂系统控制中,是由于该控制方法可使系统进入滑动模态状态,形成模型跟踪控制[ 1]。具有可以消除系统内部的耦合,实现解耦的优点。而且对系统参数变化和干扰不敏感,无需精确的数学模型[ 2]。但当系统到达滑模面时,将在滑模面附近不停切换,这样便会出现较强的抖振现象。为了解决抖振问题,近年来国内外学者提出了很多改进的方法,例如自适应终端滑模变结构控制[ 3]、神经网络滑模变结构控制[ 4]、模糊滑模变结构控制[ 5]、终端滑模变结构控制[ 6]等方法,将滑模控制与其他算法相结合以可有效地减少滑模控制的抖振现象。其中终端滑模变结构控制方法是在滑模控制中引入非线性函数,目的是使得系统到达滑模面后控制误差能快速地收敛到零,从而有效地降低系统的抖振现象。
多自由度机械臂是一种非线性、强耦合的复杂系统,滑模控制又可以很好地解决这类系统具有的控制问题,因此滑模控制一直以来都被广泛用于机器人的控制之中,例如林雷等[ 7]将模糊控制引入到滑模变结构中,有效地降低了控制器的抖振,并实现了机器人快速跟踪控制的仿真。薛力军等[ 8]将自适应终端滑模控制引入到空间机器人控制中。Feng等[ 9]提出非奇异终端滑模控制(NTSM)方法并实现两关节机械臂的控制。
本文在文献[ 9]提出的控制方法的基础上,提出了一种新的非奇异性快速终端滑模控制方法,并应用于六自由度机械臂的位姿控制中,在空载有、无扰动条件和负载无扰动条件下将其控制效果与PID控制效果进行比较。
六自由度机器臂的系统动力学模型如下:
D( θ) 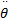
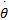
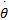
式中: θ, 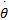
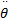
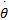
值得指出的是,惯量项和重力项在机械臂的控制中特别重要,它们直接影响机械臂系统的稳定性和定位精度。科里奥利力和向心力项只有在机器臂高速运动情况下才有意义,否则它们对机械臂系统几乎不会产生影响。也就是说,在运动速度不高的情况下,可以忽略系数 C( θ, 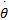
D( θ) 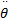
将六自由度机械臂的动态方程转化为各关节子系统的状态方程,由式(2)得:
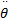
令:
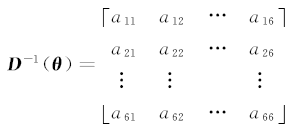 | (4) |
则:
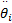
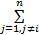
式中: i=1,2,…,6。
将各关节的方程(5)转化为二阶非线性模型:
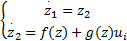 | (6) |
式中:z1=θi;z2= 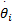
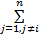
针对式(6)所代表的非线性系统,结合线性滑动模态与快速终端滑动模态的形式,将快速终端滑动模态表示为:
s1=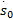 +β +β 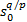 | (7) |
式中: β>0,且 q、 p( p>q)为互质的正奇数,这里选取 p=5, q=3。
设 r i为关节角度转动指令信号,令:

由式(7)可知:
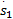 = = 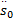  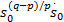 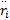  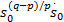 | (8) |
选择的快速终端滑模控制律为:
u i =-g -1( z)[ f( z)- 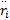

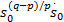
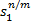
式中: φ、 γ>0,且 m、 n( m>n)为互质的正奇数,这里选取 m=5, n=3。
当 s1=0时,由式(7)得:
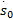
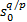
系统在滑模面上从任意 s0(0)≠0状态到达平衡状态 s0=0的滑模运动时间为:
t s=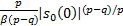 | (11) |
由常规滑动模态(式(7))所得到的位姿控制律(式(9))可知( q-p) /p<0,当系统的状态达到或接近关节角度转动指令信号时, s0≈0。此时,控制器输出趋于无穷,控制律(式(9))存在奇异问题,在实际运行中容易出现失调,所以需要对其做进一步修改。
为了解决传统快速终端滑模控制的奇异问题,在这里,引入非奇异快速终端滑模控制方法[ 8]。选取的非奇异滑模面为:
s1 =s0+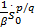 | (12) |
可以看出当 s1=0时,式(12)与式(7)等价,所以此时系统滑模运动时间 t s和式(11)相同。
选择的非奇异快速终端滑模控制律为:
u i =-g -1( z)[ f( z)- 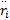


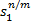
式中: φ、 γ>0,且 m、 n( m>n)为互质的正奇数,这里选取 m=5, n=3。
为了证明选取的控制律可使系统在有限时间内到达滑模面。采用 Lyapunov方法,选取 Lyapunov函数为:
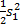 | (14) |
结合式(12)(13)得:
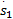
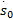
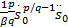
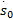
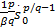
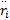
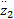
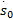
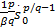
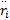
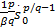
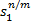
所以:
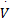
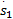
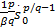
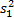
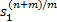
式中: φ, γ>0; q和 p( p>q), m和 n( m>n)均为互质的正奇数。
所以 
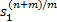
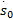
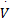
又由:
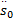
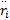
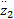
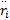

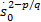
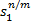
当 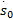
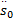
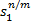
由于 m和 n( m>n)为互质的正奇数,所以当 s1>0时, 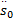
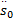
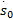
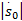
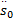
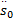
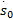
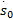
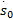
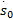
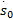
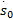
综合以上分析可知,选择的非奇异快速终端滑模控制律(式(13))可使系统在有限时间内到达滑模面,并沿着滑模面运动到达平衡状态。
对上面提出的非奇异快速终端滑模控制器进行不确定系统的稳定性分析。考虑到系统的不确定性,将各关节子系统二阶非线性模型表达为
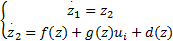 | (16) |
式中: d( z)表示系统的不确定性和外部干扰的总和,设 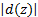
选择快速终端滑模控制律形式同式(13):
u i =-g -1( z)[ f( z)- 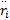

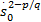
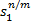
式中: γ'= 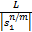
选取 Lyapu nov函数为:
V= 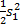
结合式(12)(16)得:
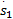
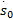
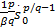
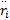
将式(17)代入式(18)得:
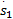
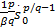
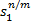
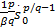
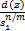
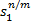
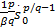
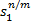
式中: γ″=γ'+ 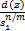
由 γ'> 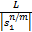
γ″>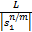 + + 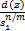 | (20) |
讨论:
①当 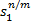
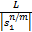
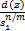
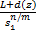
②当 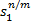
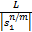
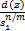
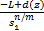
即: γ″> 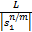
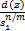
于是:
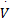
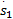
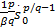
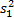
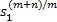
由于 m+n为偶数,且 φ, γ″≥0则 -φ 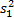
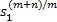
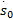
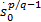

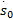
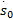
由此,也说明当选取适当的控制律参数 γ时,所设计的非奇异快速终端滑模控制器对有界不确定性或干扰具有鲁棒性。
试验中的控制对象为六自由度机械臂,设置各关节运动速度均小于10 °/s,每种算法下控制器的输出幅值均限制在-10 ~10 N· m之间。设定各关节目标位置为 θ1=20 °, θ2=-10 °, θ3=-15 °, θ4=30 °, θ5=80 °, θ6=-90 °。
分别进行3种情况下的位姿控制试验:空载无扰动试验;空载有扰动试验;负载试验(加载重物为2 .5 kg)。控制器参数如表1所示。
| 表1 非奇异快速终端滑模控制器参数 Table 1 Parameters of NTSM |
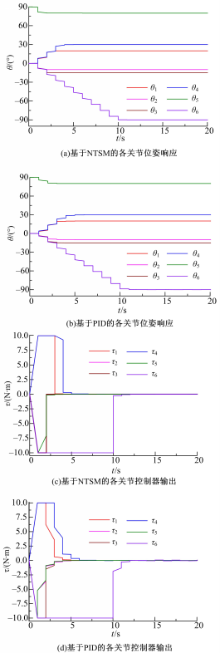
各关节输出响应曲线如图1所示。从图1(a)中可以看出,在速度限定的条件下,前5个关节均在5 s内收敛到目标位置;第6个关节较慢,约为10 s,这是由于其运动范围较大所引起的。但各关节收敛时间均可通过调节控制器的参数来改善,调节时间越短,控制器的输出量越大。对比试验数据发现,系统稳定后,各关节稳态误差均小于0.008°。从图1(c)各关节控制器输出曲线可以看出,控制器输出瞬间达到饱和状态,且饱和状态持续,直至系统收敛到平衡状态。这种控制器的输出形式使得各关节收敛时间大大减少。
进一步采用PID控制策略对六自由度机械臂各关节位置进行控制,目的是为了将非奇异快速终端滑模控制效果与PID控制效果进行比较。
从图1(b)中可以看出:基于PID控制下的各关节位置响应曲线同样在较短的时间内收敛到平衡状态。分析试验数据可以发现,基于PID控制下的各关节响应均有不同程度的超调量;由图1(d)可以看出:控制器的输出在瞬间达到了饱和,对照图1(b)可以看出:当控制器输出达到饱和时,关节角度以最快的速率向平衡状态趋近;当系统处于稳态时,只要偏差存在,控制器就会有输出值,以不断调整各关节位置收敛到平衡状态。
为了定量地总结出两种方法下系统的控制性能指标,对所获得的试验数据进行分析计算,其结果如表2所示。
| 表2 空载无扰动条件下两种方法的各关节控制性能指标 Table 2 No-load control performance index of two algorithm without disturbance |
从表2可以看出,基于非奇异快速终端滑模控制的六自由度机械臂各关节调节时间较PID控制均有不同程度的减少,且实现了各关节的无超调控制,稳态精度数量级均达到了10-3,这表明采用非奇异快速终端滑模控制方法可以实现六自由度机械臂各关节的高精度协调控制。而PID控制在以牺牲系统动态特性的条件下,换来了相对较短的调节时间和相对较高的稳态精度,这在实际的工业场合中是绝对不允许的。
本试验在控制器的输出中加入了扰动量,幅值为5,持续时间为500个程序循环周期。
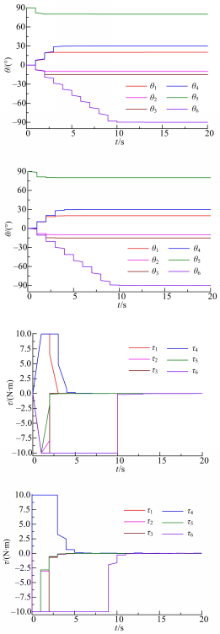
由图2(a)和图2(c)可以看出,在程序运行13 s时,各关节控制器输出中加入了扰动量。但此时各关节位置偏移很小,甚至看不出来,这说明在外界扰动存在的条件下,非奇异快速终端滑模控制具有较强的鲁棒性。由图2(b)和图2(d)可以看出:扰动量的加入时间大约是16 s,当系统存在外界扰动时,控制器的输出达到饱和状态,以确保机械臂各关节在较短的时间内恢复到原平衡状态。但该算法下的整个控制系统对外界扰动较为敏感,各关节位置的变化量较大,虽然具有较快的调节速率,但相对较大的位置偏移量,仍然无法实现整个调节过程的快速性,快速的调节速率是以牺牲较大的能量为代价的。
为了模拟实际工作环境下机械臂搬运重物的动作,在机械臂末端执行器上加载重物后,进行机械臂的位姿控制试验的输出响应曲线如图3所示,对比图1可以看出:在空载和负载两种情况下,NTSM控制策略与PID控制策略的各关节输出变化基本相同。对所获得的试验数据进行分析计算,结果如表3所示。
| 表3 负载条件下两种方法的各关节控制性能指标 Table 3 Control performance index of two algorithm with load |
对比空载和负载两种情况,两种控制策略下的各关节位姿控制的综合调节时间没有发生太大的变化,说明负载对机械臂的控制时间影响不是很大。观察NTSM控制时的关节3、5可以发现:有负载时出现了超调,而PID有负载控制时每个关节还是都出现了超调,说明由于负载的存在,惯性增大后,超调现象是不可避免的,NTSM控制可以减少超调现象,但不能完全避免。
从图3(c)和图3(d)各关节控制器输出曲线可以看出:基于NTSM控制时,控制器输出在无超调的情况下是从一个方向无限接近于零,有超调时控制器输出值符号改变后从另一个方向无限接近于零,而不会再次改变符号,这样控制器输出使得机械臂在达到平衡状态后无振动现象;而基于PID控制时,在机械臂到达平衡状态时控制器输出值在零附近不停地改变符号,使得机械臂在平衡状态附近不停地振动。
通过以上分析可知:NTSM控制可以使机械臂快速、精确、超调量少、无抖震地到达目标位姿,因此适合精度要求高、超调量少的实时作业中,例如焊接、零件装配等高精度作业;而PID控制是以牺牲系统动态特性的条件下,换来了较短的调节时间,因此更适合要求控制时间短但稳定性不高的生产作业中,例如物体的搬运、分类等快速的生产作业中。
针对六自由度机械臂本体研究了各关节协调运动控制技术,考虑到该系统多输入多输出的特性,将整个系统看作是单关节多个状态变量耦合的SISO系统的组合,采用非奇异快速终端滑模控制方法设计了六自由度机械臂各关节子系统控制器,并将其控制效果与PID控制效果做了比较。试验结果表明:非奇异快速终端滑模控制算法可以实现六自由度机械臂各关节在整个运动过程中的快速性与精确性,且对外界干扰具有较强的鲁棒性。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|