引用本文
武冬梅, 丁海涛, 郭孔辉. 基于线性估计模型的电动汽车质心侧偏角估计. 2014, 44(4): 901-906
[WU Dong-mei, DING Hai-tao, GUO Kong-hui. Sideslip angle estimation based on linear estimation model for electric vehicle. Journal of Jilin University Engineering and Technology Edition, 2014, 44(4): 901-906]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
基于线性估计模型的电动汽车质心侧偏角估计
武冬梅, 丁海涛, 郭孔辉
吉林大学 汽车仿真与控制国家重点实验室,长春130022
通信作者：丁海涛（1974-）,男,教授.研究方向:汽车动力学仿真与控制.E-mail:ding_hai_tao@126.com

作者简介：武冬梅（1986-）,女,博士研究生.研究方向:汽车动力学仿真与控制.E-mail:dongmei420504@163.com

基金:&#x 0201c;863”国家高技术研究发展计划项目(2012AA110904,2011AA11A221); “973”国家重点基础研究发展计划项目(2011CB711205);
摘要

质心侧偏角估计是车辆稳定性控制系统中的关键技术和难点,针对电动汽车,本文充分利用车轮上的驱动力矩和制动力矩信息,计算出了轮胎上的纵向力。并将轮胎侧向力用纵向力和侧偏角表示或进行局部线性化。这样可以将二自由度车辆模型简化为以侧向速度为状态的线性估计模型,用于电动汽车质心侧偏角的估计。仿真结果表明:基于线性估计模型的质心侧偏角估计器的估计精度较高,对路面摩擦因数的依赖程度小,并且计算简单,可以应用于车辆的稳定性控制系统中。

关键词: 车辆工程; 质心侧偏角估计; 线性估计模型; 稳定性控制; 卡尔曼滤波
中图分类号:U461.6 文献标志码:A 文章编号:1671-5497(2014)04-0901-06
Sideslip angle estimation based on linear estimation model for electric vehicle
WU Dong-mei, DING Hai-tao, GUO Kong-hui
State Key Laboratory of Automotive Simulation and Control,Jilin University,Changchun 130022, China
Abstract

Sideslip angle estimation is the key technique of vehicle stability control system. For electric vehicle, the information of driving torque and braking torque on wheels can be fully utilized to calculate the longitudinal force on the tire. If the longitudinal slip of the tire is large enough, the lateral force on the tire can be expressed with the longitudinal force on the tire and the tire slip angle. If the longitudinal slip of the tire is small, the nonlinear tire model is locally linearized. In such way, the two degrees of freedom vehicle model can be simplified to a linear model, whose state variable is the vehicle lateral speed and can be used to estimate the sideslip angle of the vehicle. Simulation results show that the estimation accuracy of the sideslip angle with the linear estimation model is high enough, and its dependence on the road surface friction coefficient is small. In addition, the calculation is simple due to the linearity of the model. The estimation method can be applied to the vehicle stability control system.

Keyword: vehicle engineering; sideslip angle estimation; linear estimation model; stability control; Kalman filter

质心侧偏角和横摆角速度是表征车辆稳定性的重要指标,是稳定性控制系统中的主要控制变量[ 1, 2]。实际中车辆的横摆角速度比较容易测量,而质心侧偏角的测量比较困难,所以需要对其进行估计。质心侧偏角估计是车辆稳定性控制系统中的关键技术和难点,国内外开展了大量的研究工作[ 3, 4, 5, 6, 7, 8]。文献[3]基于线性车辆模型,利用卡尔曼滤波方法估计质心侧偏角,但只适用于车辆的线性工作区。文献[4-5]采用了扩展卡尔曼滤波,文献[6]采用了非线性状态观测器,文献[7]采用了滑模观测器,文献[8]采用了神经网络方法,这些方法都是基于非线性估计模型,模型维数多,非线性估计算法复杂,并且对路面摩擦因数的依赖程度大,在实际控制系统应用中受到限制。

在文献[1-2]中,Bosch公司提出了利用线性估计模型进行质心侧偏角估计的方法,在轮胎线性区和非线性区都成立,但只适用于轮胎纵向滑移率较大的工况。在纵向滑移率较小时采用积分法估计质心侧偏角,误差较大。本文借鉴Bosch公司线性估计模型的思想,提出在全工况下都适用的线性估计模型,结合路面摩擦因数估计,对电动汽车的质心侧偏角进行估计。

1 卡尔曼滤波和扩展卡尔曼滤波

本文中的质心侧偏角估计利用线性估计模型,采用卡尔曼滤波方法,其中路面摩擦因数估计采用扩展卡尔曼滤波方法[ 9, 10]。卡尔曼滤波是一种用于线性离散系统的无偏、最小方差估计。

对于线性离散系统,状态方程为:

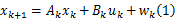
式中: xk+1为 k+1时刻的系统状态; xk为 k时刻的系统状态; Ak为状态矩阵; Bk为输入矩阵; wk为系统噪声。

系统测量方程为:

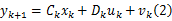
式中: yk+1为 k+1时刻的系统输出; Ck为观测矩阵; Dk为前馈矩阵; vk为测量噪声。

假设系统噪声 wk和测量噪声 vk都是零均值的白噪声,且两者互不相关。

卡尔曼滤波算法可分为两部分:预测过程和校正过程。预测过程根据状态方程通过当前时刻的系统状态预测下一时刻的状态;校正过程用观测结果作反馈,对预测结果进行校正,得到系统的最优估计。

卡尔曼滤波预测过程:

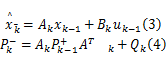
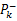
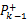
式中: 为 k时刻的状态预测值; 为 k时刻的误差协方差矩阵预测值; 为 k-1时刻的误差协方差矩阵估计值; Qk为系统噪声的相关矩阵。

校正过程:

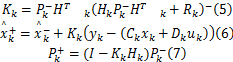
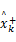
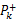
式中: Kk为卡尔曼滤波增益矩阵; 为 k时刻的状态估计值; 为 k时刻误差协方差矩阵的估计值; Rk为测量噪声的相关矩阵。

如果是非线性系统,系统状态方程为:

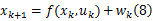
系统测量方程为:

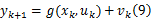
扩展卡尔曼滤波是在卡尔曼滤波基础上,围绕估计值 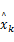将非线性函数 f( xk, uk)和 g( xk, uk)展开成泰勒级数并略去二阶以上的项来进行线性化,就可以采用与线性卡尔曼滤波一样的预测过程和校正过程进行状态估计。

线性化的状态转移矩阵为:

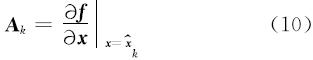
线性化的测量矩阵为:

2 质心侧偏角线性估计模型
2.1 车辆动力学模型

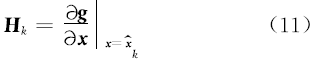
由于车辆的质心侧偏角主要可以从侧向和横摆运动上反映出来,所以选用包含侧向和横摆运动的二自由度车辆模型作为分析模型,如图1所示。为了充分考虑车轮纵向力和侧向力的影响,所以模型中包含了4个车轮的受力,但假设左、右轮的侧偏角相同。

图1 二自由度车辆模型Fig.1 2-DOF vehicle model

车辆侧向和横摆方向的动力学方程为:

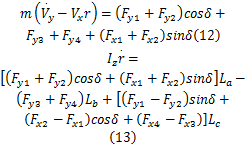
式中: m为整车质量; Iz为车辆绕 z轴的转动惯量; Vy、 Vx为车辆的侧向和纵向速度; r为车辆的横摆角速度; δ为前轮转角; Lc为半轮距; La、 Lb为质心到前轴和后轴的距离; Fx1、 Fx2、 Fx3、 Fx4为4个车轮的纵向力; Fy1、 Fy2、 Fy3、 Fy4为4个车轮的侧向力。

2.2 轮胎模型

在进行车辆质心侧偏角估计时采用第一种形式的HSRI非线性轮胎模型,这种轮胎模型考虑了轮胎的非线性,同时形式简单,纵向力和侧向力的关系比较容易表达 。模型中纵向力和侧向力的表达式为:

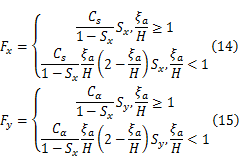
式中: Cs为轮胎的纵滑刚度; Cα为轮胎的侧偏刚度; Sx为轮胎的纵向滑移率; Sy为轮胎的侧向滑移率。

式(14)和式(15)中的 ξa/H表达式如下:

式中: μ为路面摩擦因数; Fz为轮胎的垂直载荷。

在纵向滑移率 Sx较大时,纵向力和侧向力的耦合特性明显。由轮胎模型可以看出二者的耦合关系,并且用轮胎纵向力和侧向滑移率表示侧向力:

在 Sx较小时,纵向力和侧向力的耦合特性不明显,不能再用式(17)计算侧向力,而仍然采用HSRI轮胎模型计算,所以 Fy可以表示成统一形式:

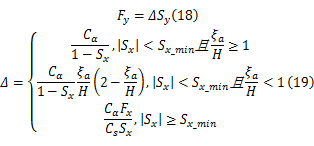
式中: Sx_min是一个较小的纵向滑移率限定值,本文取为0.05。

2.3 线性估计模型

将 Fy1、 Fy2、 Fy3、 Fy4用式(18)表达,代入式(12)(13)得到:

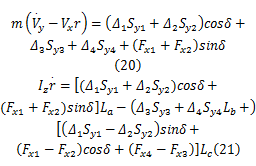
假设两前轮的侧向滑移相同,两后轮的侧向滑移相同,则有:

将 Sy1、 Sy2、 Sy3、 Sy4代入式(20)(21)整理得到:

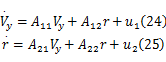
式中:

A11 =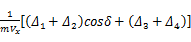

A12 =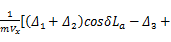

+Vx

u1 =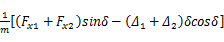

A21 =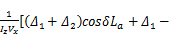

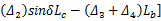
A22 =

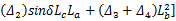
u2 =

δ+ sin δLa

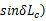
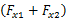
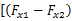
cos δ+ 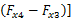Lc

在集中式和分布式驱动电动汽车上,车轮上的驱动力矩都可以通过电机力矩计算出来。而电动汽车上采用电子液压制动系统,内部含有制动轮缸压力传感器,所以制动轮缸压力是可测的。在车轮没有发生抱死和滑转时,可以计算得到轮胎的纵向力:

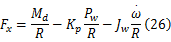
式中: Md为车轮上的驱动力矩; R为轮胎半径; Kp为制动效能因数; Pw为轮缸压力; Jw为车轮转动惯量; 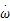为车轮转动角加速度。

当轮胎纵向滑移率很小时, Δ的表达式中含有侧向滑移率 Sy,即含有 Vy。但在此时不将 Vy作为状态量,而是作为一个参数量简化处理,即用前一时刻 Vy的估计值计算。如果给定一个初始侧向速度 Vy0,则可以循环计算得到 Δ。纵向速度 Vx可以通过估计得到,这里假设是已知的。因此 A11、 A12、 u1、 A21、 A22、 u2都可以计算得到,并且简化后与状态 Vy无关,则式(24)(25)是以 Vy为状态的线性状态方程和测量方程,可用作质心侧偏角的线性估计模型。

3 质心侧偏角估计器设计

在计算机程序中,式(24)(25)经过简单的欧拉积分得到差分方程:

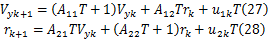
式中: T为仿真步长; k为采样时刻。

横摆角速度 r经过线性插值:

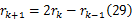
将式(29)代入式(28)得到:

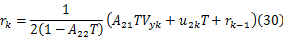
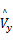
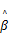
所以式(27)和式(30)可以分别作为 Vy的线性状态方程和线性观测方程,利用线性卡尔曼滤波方法可以估计出状态 ,再计算得到质心侧偏角 :

可以看出,采用的线性估计模型只有一个状态方程和一个观测方程,所以基于线性估计模型的质心侧偏角估计器只有一维的代数运算,计算简单,实时性好。估计器的输入包括:轮胎纵向力 Fx1、 Fx2、 Fx3、 Fx4,轮胎纵向滑移率 Sx1、 Sx2、 Sx3、 Sx4,横摆角速度 r,纵向车速 Vx和方向盘转角 δ。路面摩擦因数 μ作为参数,只在纵向滑移率很小时才需要,在纵向滑移率较大时不需要,所以质心侧偏角的估计精度受路面摩擦因数的影响程度较低。

4 路面摩擦因数估计

在纵向滑移率较小时,基于线性估计模型的质心侧偏角估计器需要用到路面摩擦因数的信息,所以这时必须对路面摩擦因数进行估计,本文采用扩展卡尔曼滤波方法估计路面摩擦因数。

路面摩擦因数可以通过车辆的纵向运动、侧向运动和横摆运动来反映,所以使用包括纵向、侧向和横摆三个自由度的三自由度车辆模型。

三自由度车辆动力学方程:

与质心侧偏角估计一样,路面摩擦因数估计也采用第一种形式的HSRI非线性轮胎模型。经过离散化后,将路面摩擦因数作为系统参数,用侧向加速度 ay、纵向加速度 ax和横摆角加速度 r作为可观测的输出量,得到路面摩擦因数的估计模型。

参数方程:

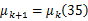
观测方程:

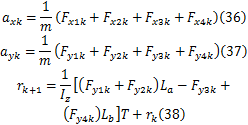
同质心侧偏角估计器一样,横摆角速度 r利用式(29)进行线性插值,则式(38)变为:

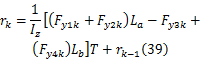
其中侧向力 Fy1、 Fy2、 Fy3、 Fy4和纵向力 Fx1、 Fx2、 Fx3、 Fx4通过HSRI轮胎模型计算,路面摩擦因数 μ作为一个参数。利用式(35)(36)(37)(39)构成估计模型,应用扩展卡尔曼滤波的方法估计路面摩擦因数。

估计路面摩擦因数时要用到质心侧偏角的信息,为了使系统结构简单、稳定,先将质心侧偏角和路面摩擦因数分别估计,再将二者联合循环运算。

5 仿真分析

在汽车动力学仿真软件veDYNA中对设计的质心侧偏角估计器进行仿真验证,veDYNA进行的车辆动力学仿真可以用于高效率的功能开发和控制系统测试。仿真验证所用的车辆模型相关参数如下: La为1.1954 m; Lb为1.2446 m; Iz为2080.724 (kg·m2);轮距2 Lc为1.455 m;前轮纵滑刚度 Csf为46840 N-1;前轮侧偏刚度 Cαf为38942 N-1;后轮纵滑刚度 Csr为46086 N-1;后轮侧偏刚度 Cαr为43810 N-1。

在veDYNA仿真平台中,分别在高附着和低附着路面上进行了闭环双移线试验、单移线制动试验。将基于线性估计模型的质心侧偏角估计算法的估计值与veDYNA中车辆模型的仿真值对比,分析估计器的估计效果。双移线试验时,轮胎纵向滑移率较小,需要估计路面摩擦因数。单移线制动试验时,轮胎纵向滑移率较大,不需要估计路面摩擦因数。

高附着路面闭环双移线试验:路面附着因数为0.8,车速为100 km/h,仿真结果如图2所示。

图2 高附着路面双移线试验的仿真结果Fig.2 Double lane change maneuver on high adhesion road surface

图3 低附着路面双移线试验的仿真结果Fig.3 Double lane change maneuver on low adhesion road surface

低附着路面上闭环双移线试验:路面附着因数为0.2,车速为70 km/h,仿真结果如图3所示。

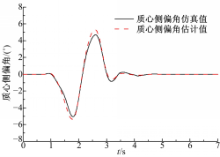
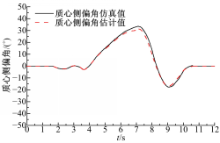
由图2和图3中的结果可以看出,在质心侧偏角小于4°的线性区内,路面摩擦因数和质心侧偏角估计值都能较好地跟随仿真值,有较高的估计精度。

高附着路面上单移线制动试验:路面附着因数为1.0,车速为80 km/h,仿真结果如图4所示。

图4 高附着路面单移线制动试验的仿真结果Fig.4 Single lane change with braking on high adhesion road surface

低附着路面上单移线制动试验:路面附着因数为0.4,车速为100 km/h,仿真结果如图5所示。

图5 低附着路面单移线制动试验的仿真结果Fig.5 Single lane change with braking on low adhesion road surface

由图4和图5中的结果可以看出,在质心侧偏角超过4°的非线性区,以及20°以上的强非线性区内,质心侧偏角估计器得到的估计值依然能较好地跟随仿真值,有较高的估计精度。

综合仿真结果可以看出,基于线性估计模型的汽车质心侧偏角估计器在不同路面上的制动和非制动工况下,在质心侧偏角的线性区和非线性区都有较好的估计效果,算法适应性较强,可以用于车辆稳定性控制系统中。

6 结束语

充分利用电动汽车上的驱动力矩和制动力矩信息计算轮胎纵向力。将轮胎侧向力用纵向力和侧偏角表示或进行局部线性化,可以将二自由度车辆动力学模型简化为以侧向速度为状态的线性估计模型,用于汽车质心侧偏角的估计。理论分析和仿真结果表明:基于线性估计模型的质心侧偏角估计器在车辆运动的线性区和非线性区都有较高的估计精度。同时计算简单,对路面摩擦因数估计精度的依赖程度小,利于在车辆稳定性控制系统中的应用。

The authors have declared that no competing interests exist.

参考文献
[1] van Zanten Anton T. Bosch ESP systems: 5 years of experience[C]∥SAE Paper, 2000-16-33. [本文引用:1]
[2] van Zanten Anton T, Erhardt Rainer, Pfaff Georg, et al. Control aspects of the Bosch-VDC[C]∥International Symposium on Advanced Vehicle Control, Aachen University of Technolgy, 1999: 573-607. [本文引用:1]
[3] Paul J, Venhovens T H, Naab K. Vehicle dynamics estimation using Kalman filters[J]. Vehicle System Dynamics, 1999, 32(2-3): 171-184. [本文引用:1] [JCR: 0.766]
[4] 宗长富, 胡丹, 杨肖, 等. 基于扩展Kalman滤波的汽车行驶状态估计[J]. 吉林大学学报: 工学版, 2009, 39(1): 6-11.
Zong Chang-fu, Hu Dan, Yang Xiao, et al. Vehicle driving state estimation based on extended Kalman filter[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(1): 6-11. [本文引用:1] [CJCR: 0.701]
[5] 宗长富, 郑宏宇, 徐颖, 等. 基于信息融合技术的汽车状态估计算法[J]. 吉林大学学报: 工学版, 2008, 38(2): 1-4.
Zong Chang-fu, Zheng Hong-yu, Xu Ying, et al. Study in vehicle state esitmation based on the information fusion algorithm[J]. Journal of Jilin University (Engineering and Technology Edition), 2008, 38(2): 1-4. [本文引用:1] [CJCR: 0.701]
[6] Kiencke U, Daiss A. Observation of lateral vehicle dynamics[J]. Control Engineering Practice, 1997, 5(8): 1145-1150. [本文引用:1] [JCR: 1.669]
[7] Stephant J, Charara A, Meizel D. Evaluation of a sliding mode observer for vehicle sideslip angle[J]. Control Engineering Practice, 2004, 15(7): 900-910. [本文引用:1] [JCR: 1.669]
[8] Lin Fen, Zhao You-qun. A comparison of two soft-sensing methods for estimating vehicle side slip angle[C]∥SAE Paper, 2007-01-3587. [本文引用:1]
[9] 鲍奇克SM. 数字滤波和卡尔曼滤波[M]. 凌云旦译. 北京: 科学出版社, 1984. [本文引用:1]
[10] Simon Haykin. 自适应滤波器原理[M]. 4版. 郑宝玉译. 北京: 电子工业出版社, 2003. [本文引用:1]
[11] Tielking John T, Mital Naveen K, Pfaff Georg. A comparative evaluation of five traction tire models[R]. Interim Document 6, Michigan: Highway Safety Research Institute, University of Michigan, 1974. [本文引用:1]