基于最优控制理论的智能车辆轨迹生成方法

引用本文

李爱娟, 李舜酩, 赵万忠, 沈峘, 江星星, 邱绪云, 王慧君. 基于最优控制理论的智能车辆轨迹生成方法. 吉林大学学报: 工学版, 2014, 44(5): 1276-1282[LI Ai-juan, LI Shun-ming, ZHAO Wan-zhong, SHEN Huan, JIANG Xing-xing, QIU Xu-yun, WANG Hui-jun. Optimal control theory based trajectory generation method for intelligent vehicle. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1276-1282] 复制到剪切板

Permissions

基于最优控制理论的智能车辆轨迹生成方法

李爱娟^1,², 李舜酩², 赵万忠², 沈峘², 江星星², 邱绪云¹, 王慧君¹

1.山东交通学院汽车工程学院, 济南 250023

2.南京航空航天大学能源与动力学院, 南京 210016

通信作者:李舜酩(1962-),男,教授,博士生导师.研究方向:车辆动力学系统.E-mail:smli@nuaa.edu.cn

李爱娟(1980-),女,讲师,博士.研究方向:汽车动力学系统与控制.E-mail:liaijuan2008@gmail.com

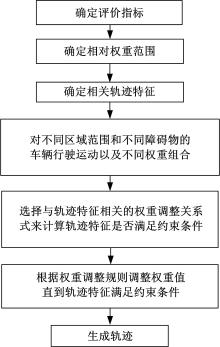
基金:国家自然科学基金项目(51375007); 中国博士后科学基金项目(2011M500917); 江苏省博士后科研计划项目(1101153C)

摘要

为了能够生成适应不同道路环境的动态轨迹,在最优控制理论的基础上进行了改进,在方法中建立了包括3个常用评价指标:时间、消耗能量和距离障碍物最短距离的动态评价函数,研究了不同权重系数对轨迹特征影响的规律,进而得出了启发式权重调整规则和调整流程。仿真结果表明,本文提出的基于最优控制理论的轨迹规划方法是有效可行的,得出的权重调整方法是正确的,使用本文方法可以生成适用于不同道路环境的动态行驶轨迹,且轨迹满足多种约束条件。

关键词: 车辆工程; 智能车; 最优控制; 轨迹生成; 权重调整

中图分类号:U471.15 文献标志码:A 文章编号:1671-5497(2014)05-1276-07

Optimal control theory based trajectory generation method for intelligent vehicle

LI Ai-juan^1,², LI Shun-ming², ZHAO Wan-zhong², SHEN Huan², JIANG Xing-xing², QIU Xu-yun¹, WANG Hui-jun¹

1.School of Automotive Engineering, Shandong Jiaotong University, Ji'nan 250023,China

2.College of Energy and Power Engineering, Nanjing University of Aeronautics & Astronautics, Nanjing 210016, China

Abstract

In order to generate feasible dynamic trajectory adapting to different road environments, the traditional trajectory generation method is improved based on the optimal control theory. The dynamic cost function is created, which includes three cost terms, time, energy, and clearance from obstacles. The influence of different weights to the trajectory features is studied, and the heuristic weight regulation rules and regulation procedure are obtained. The simulation results show that the improved trajectory generation method is feasible. The weight regulation rules and procedure are right; the optimal driving trajectory can be dynamically generated. Several constraints are obtained and the driving trajectory can adapt to different road environments.

Keyword: vehicle engineering; intelligent vehicle; optimal control; trajectory generation; weight regulation

Show Figures

0 引言

智能车辆是智能交通系统的重要组成部分,国际上众多的研究机构及工业设计单位对其研发过程正投入大量的人力、物力,时刻关注着关键技术的研发^{[ 1, 2]}。轨迹规划技术是车辆进行自动行驶的一项关键技术^{[ 3, 4]}。轨迹规划的目的是要在适当的限制条件下,生成车辆运动轨迹的状态表达式,作为跟踪控制系统的控制输入^{[ 5]}。

早期的轨迹规划方法主要是用不同的函数(例如 $\begin{matrix} B \end{matrix}$ 样条函数,多项式函数,正弦函数以及圆弧等)来模拟轨迹,并对车辆这一非线性系统施加多种约束条件,在约束条件范围内求解可行的轨迹^{[ 6, 7]}。早期方法中规划轨迹的参数不能实现在线动态调整的功能,所以生成的轨迹不能动态适应连续变化的道路环境。最优控制方法主要对评价函数施加不同的约束条件从而求出最优轨迹,但是最优控制方法中由于评价函数的权重不能实现在线调整,所以规划的轨迹也不能动态适应变化的道路环境^{[ 8, 9]}。

本文提出一种基于最优控制理论的轨迹生成方法,建立多目标动态评价函数,并通过研究评价函数中不同评价指标的权重对轨迹特征影响的规律,得出权重调整规则和调整流程,使得轨迹能够根据周围的环境进行动态调整优化,以生成最优行驶轨迹。

1 多目标动态评价函数

运用最优控制方法进行轨迹规划,其目的是求出可用的控制输入变量 $\begin{matrix} u {(t)}^{*}, 使得以微分方程描述的系统式 (1) 能够沿着可行的最小化评价函数 (2) 的轨迹 x {(t)}^{*} \end{matrix}$ 进行循迹行驶^{[ 10]}。

$\begin{matrix} \begin{matrix} \overset{\cdot}{x} (t) = f (x (t), u (t), t) (1) \\ J (u) = \int_{t_{0}}^{t_{f}} g (x (t), u (t), t) dt (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} t 为时间; t_{0} 和 t_{f} \end{matrix}$ 分别为车辆的起始和终止时间。

对所有的 $\begin{matrix} t \in [t_{0}, t_{f}] \end{matrix}$ 及固定的初始时刻与初始状态、终止时刻和终止状态,有边界条件:

$\begin{matrix} x (t_{0}) = x_{0}; x (t_{f}) = t_{f} (3) \end{matrix}$

改进的最优控制方法中对消耗能量、完成时间和距离障碍物的最短距离3个评价指标函数进行优化,评价函数如式(4)所示,权重向量为 $\begin{matrix} [W_{1}, W_{2}, W_{3}, L_{IM}] 。 \end{matrix}$

$\begin{matrix} J = \int_{t_{0}}^{t_{f}} (W_{1} + W_{2} \sum_{i \in \{O\}} (b_{i} (g_{i})) + W_{3} U^{2} (t)) dt (4) \end{matrix}$

完成时间: $\begin{matrix} W_{1} 是完成时间的权重, 因为评价函数 J 是时间段 [t_{0}, t_{f}] 上的积分形式, 所以需要一个常系数 W_{1} \end{matrix}$ 对时间进行优化。

消耗能量:对消耗能量的表达方式进行简化, $\begin{matrix} U^{2} (t) 表示消耗能量, U (t) 为控制量, W_{2} \end{matrix}$ 为消耗能量的权重。

距离障碍物的最短距离:为了使得车辆在行驶过程中不与障碍物相撞,在评价函数中设定一项评价指标 W₃ $\begin{matrix} \sum_{i \in \{b\}} \end{matrix} \begin{matrix} (b_{i} (g_{i})) \end{matrix}$ ,其中W₃为距离障碍物最短距离的权重, $\begin{matrix} b_{i} (g_{i}) 为补偿函数, 当车辆靠近障碍物 i 时, 补偿函数值增加; 反之, 当车辆远离障碍物时, 补偿函数值减小。 g_{i} 为智能车距离障碍物中心 i 的距离, g_{i} \end{matrix}$ 的表达式为:

$\begin{matrix} g_{i} = \sqrt[]{(x - x_{0})^{2} + (y - y_{0})^{2} + (z - z_{0})^{2}} (5) \end{matrix}$

式中:(x₀,y₀,z₀)为车辆质心处的坐标。

当智能车在障碍物中心,即距离障碍物的中心为0时,补偿函数 $\begin{matrix} b_{i} (g_{i}) \end{matrix}$ 取最大值M _AX;当智能车在障碍物边缘,即距离障碍物中心的距离为 $\begin{matrix} h_{i} 时, 补偿函数为固定值 K; \end{matrix}$ 在距离障碍物边缘为限值L _IM时补偿函数的值减小为零。L _IM的值就是补偿函数为零时,车辆距离障碍物边缘的距离值。补偿函数在障碍物中心、障碍物边缘和距离障碍物边缘固定的距离处都有固定的值,补偿函数的系数根据障碍物的尺寸进行确定。关于补偿函数的取值和函数平滑的约束条件如下:

$\begin{matrix} \{\begin{matrix} b_{i} (0) = M_{AX}, b_{i} (R_{i}) = K \\ b'_{ileft} (h_{i}) = b'_{irig h t} (h_{i}); b ″_{ileft} (h_{i}) = b ″_{irig h t} (h_{i}) \\ b_{i} (h_{i} + L_{IM}) = 0 \\ b'_{i} (h_{i} + L_{IM}) = 0 \\ b ″_{i} (h_{i} + L_{IM}) = 0 \end{matrix} (6) \end{matrix}$

$\begin{matrix} b_{i} (g_{i}) 的取值只有在智能车距离障碍物中心 i 的距离 g_{i} 小于 R_{i} + L_{IM} \end{matrix}$ 时才有意义,即:

$\begin{matrix} b_{i} (g_{i}) = \{\begin{matrix} K (c_{1} g_{i}^{3} + c_{2} g_{i}^{2} + c_{3} g_{i} + c_{4}), g_{i} \leq h_{i} \\ K (c_{5} g_{i}^{3} + c_{6} g_{i}^{2} + c_{7} g_{i} + c_{8}), \\ h_{i} < g_{i} \leq h_{i} + L_{IM} \\ 0, g_{i} > h_{i} + L_{IM} \end{matrix} (7) \end{matrix}$

式中: $\begin{matrix} M_{AX} 和 K 通过试验进行选择, 式 (6) 中, 当车辆接触到障碍物时补偿函数的值等于 K; 系数 c_{i} (i = 1, \dots, 8) \end{matrix}$ 可以通过两个三次多项式及其一阶、二阶微分方程进行求解。

在分析改变距离障碍物最短距离的权重对轨迹生成的影响时,不仅改变 $\begin{matrix} W_{3}, 而且包括改变 L_{IM} \end{matrix}$ 的值。

2 权重对轨迹特征的影响

为了对轨迹进行调整需要有不同权重对轨迹特征影响的规律做基础,为此本文采用仿真分析的方法研究权重值对不同轨迹特征的影响规律。轨迹的特征主要是连续轨迹的数字属性,在某种程度上量化所有的轨迹特征,一般是轨迹特征约束条件的最大最小值和解释整条轨迹的平均值。轨迹的特征包括与时间相关的特征(消耗能量、运行时间、最大速度和最大加速度);与距离相关的特征(距离障碍物的最短距离)等。

2.1 权重比值对与时间相关轨迹特征的影响

不同行驶区域范围和不同障碍物环境中,权重比值对与时间相关轨迹特征的影响曲线如图1 ~图3所示。其中不同权重比时,由仿真计算得出的轨迹特征值在图中用不同的点表示。

	Figure Option View Download New Window
	图1 不同区域范围内无障碍物环境中权重比 W₃ /W₁对时间相关轨迹特征的影响Fig.1 Influence of weight ratio W₃/W₁ on trajectories’ features in different region environments without obstacles

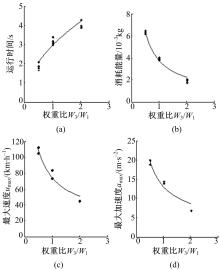	Figure Option View Download New Window
	图2 单障碍物环境中权重比 W₃/ W₁对时间相关轨迹特征的影响Fig.2 Influence of weight ratio W₃/ W₁ on trajectories’ features of time in an obstacle enviroment

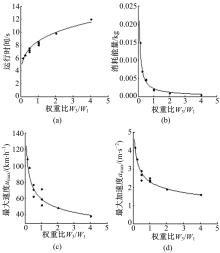	Figure Option View Download New Window
	图3 多障碍物环境中权重比 W₃/ W₁对时间相关轨迹特征的影响Fig.3 Influence of weight ratio W₃/ W₁ on trajectories’ features of time in the multi-obstacle enviroment

图1为不同区域范围无障碍物环境中权重比值对轨迹特征影响的曲线图,从图1( a)可以看出,当W₃ /W₁的值较小时,也就是消耗能量权重W₃比时间权重W₁小很多时,运行时间最短,也就是说,当把时间看作是比消耗能量重要的权重时,应该用较短的时间来完成轨迹的行驶。随着W₃ /W₁比值的增长,即W₃和W₁的值相等,然后W₃的值超过W₁的值,这样消耗能量的权重比时间的权重更重要,由图1( a)可以看出,轨迹运行的时间是相应增长的。图1( b)是权重比值W₃ /W₁对消耗能量影响的曲线图,同样当W₃ /W₁的值较小时,时间比消耗能量重要,所以轨迹的耗油量比较大,随着W₃ /W₁比值的增长,消耗能量逐渐比时间重要,轨迹消耗能量相应地减小。由图1( c)( d)可知,当W₃ /W₁的值较小时,时间权重比消耗能量权重更重要,所以轨迹的最大速度和最大加速度比较大,随着W₃ /W₁比值的增长,消耗能量权重逐渐比时间权重更重要,最大速度和最大加速度相应地降低。这与车辆如果想获得较短运行时间,需要车速和加速度高一些,而高的加速度需要消耗能量大一些的情况相对应。

图2、图3分别为单障碍物和多障碍物环境中权重比值对轨迹特征影响的曲线图。有障碍物环境和没有障碍物环境中权重比对轨迹特征的影响规律也有相似之处,当W₃ /W₁的值较小时,时间权重比消耗能量权重重要,运行轨迹需要的消耗能量比较大,最大速度和最大加速度比较高;随着W₃ /W₁比值的增长,消耗能量逐渐比时间重要,运行轨迹需要的消耗能量相应减小,最大速度和加速度相应降低,所以该影响规律可以作为对权重进行调整的有用规律。

2.2 权重比值对与距离相关轨迹特征的影响

	Figure Option View Download New Window
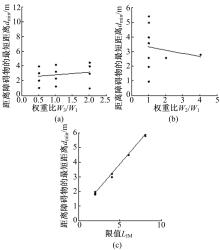	图4 多障碍物行驶环境中权重对距离障碍物最短距离的影响Fig.4 Influence of weight on minimum distance in the multi-obstacle enviroment

图4为多障碍物环境中权重对距离障碍物最短距离影响的曲线图。图4( a)为L _IM=3,W₂ /W₁ =1,W₃ /W₁的值在0 ~2 .5之间变化时,最短距离d _min的变化曲线图;图4( b)为L _IM=3,W₃ /W₁ =1,W₂ /W₁的值在1 ~5之间变化时,最短距离d _min的变化曲线图;图4( c)为W₁ =W₂ =W₃,L _IM的值在1 ~7之间变化时,最短距离d _min的变化曲线图。由图4可以看出,权重比W₃ /W₁和W₂ /W₁对最短距离d _min的影响不大,但是限值L _IM对最短距离影响较大,如果距离障碍物的最短距离约束条件不满足时,可以通过调整L _IM的值来调整距离障碍物的最短距离。

3 权重调整方法

通过第2节权重对轨迹特征影响规律的研究,可以得出权重调整规则的函数关系式,即通过调整权重值可以获得需要的轨迹特征值。从图1不同区域范围内无障碍物环境中权重比值对轨迹特征影响的曲线图中,可以得到不同区域范围内无障碍物环境中时间相关轨迹特征与权重比值W₃ /W₁的函数关系式如式(8) ~(11)所示:

$\begin{matrix} \begin{matrix} t_{f} = \{\begin{matrix} 6.732 (W_{3} / W_{1})^{0.2029}, R^{2} = 0.9967 \\ 4.53 (W_{3} / W_{1})^{0.2947}, R^{2} = 0.9893 \\ 3.417 (W_{3} / W_{1})^{0.4293}, R^{2} = 0.9958 \end{matrix} \\ (8) \\ U = \{\begin{matrix} 0.00388 (W_{3} / W_{1})^{- 0.5072}, R^{2} = 0.9993 \\ 0.002019 (W_{3} / W_{1})^{- 0.482}, R^{2} = 0.9999 \\ 0.000757 (W_{3} / W_{1})^{- 0.4163}, R^{2} = 0.9999 \end{matrix} (9) \\ v_{\max} = \{\begin{matrix} 41.31 (W_{3} / W_{1})^{- 0.5082}, R^{2} = 0.9983 \\ 3 6.13 (W_{3} / W_{1})^{- 0.4232}, R^{2} = 0.9864 \\ 30.08 (W_{3} / W_{1})^{- 0.3223}, R^{2} = 0.9789 \end{matrix} (10) \\ a_{\max} = \{\begin{matrix} 41.31 (W_{3} / W_{1})^{- 0.4586}, R^{2} = 0.9974 \\ 36.13 (W_{3} / W_{1})^{- 0.3597}, R^{2} = 0.9842 \\ 30.08 (W_{3} / W_{1})^{- 0.284}, R^{2} = 0.9866 \end{matrix} (11) \end{matrix} \end{matrix}$

式中:t _f为运行时间; $\begin{matrix} U \end{matrix}$ 为消耗能量;v _max为最大速度;a _max为最大加速度。

从图2单障碍物环境中权重比值对与时间相关轨迹特征影响的曲线图中,可以得出时间相关轨迹特征与权重比值W₃ /W₁的函数关系式为:

$\begin{matrix} \{\begin{matrix} t_{f} = 2.929 (W_{3} / W_{1})^{0.5139}, R^{2} = 0.9243 \\ U = 0.00378 (W_{3} / W_{1})^{- 0.7547}, R^{2} = 0.9855 \\ v_{\max} = 74.69 (W_{3} / W_{1})^{- 0.5569}, R^{2} = 0.9471 \\ a_{\max} = 13.14 (W_{3} / W_{1})^{- 0.597}, R^{2} = 0.9219 \end{matrix} (12) \end{matrix}$

从图3多障碍物环境中权重比值对时间相关轨迹特征影响的曲线图中,可以得出时间相关轨迹特征与权重比值W₃ /W₁的函数关系式为:

$\begin{matrix} \{\begin{matrix} t_{f} = 8.524 (W_{3} / W_{1})^{0.2177}, R^{2} = 0.9606 \\ U = 0.002229 (W_{3} / W_{1})^{- 0.9116}, R^{2} = 0.9888 \\ v_{\max} = 59.83 (W_{3} / W_{1})^{- 0.2968}, R^{2} = 0.906 \\ a_{\max} = 2.317 (W_{3} / W_{1})^{- 0.282}, R^{2} = 0.951 \end{matrix} (13) \end{matrix}$

以运行时间这一轨迹特征为例来说明启发式权重调整规则的推导过程。从式(8) ~(13)运行时间和权重比值的函数关系式可以得出,运行时间和权重比值之间的函数关系式是幂指数形式的函数关系。式(8) ~(11)中三个区域范围幂指数的平均值是0 .31,而式(8) ~(13)中运行时间和权重比的关系式中所有幂指数的平均值是0 .33,这两种情况都可以将幂指数精确到一位小数0 .3。由此可以得出运行时间和权重比W₃ /W₁之间的权重调整关系式为:

$\begin{matrix} t_{f} = q_{1} (W_{3} / W_{1})^{0.3} (14) \end{matrix}$

式中:常系数q₁可以由车辆实际行驶过程中的运行时间和W₃ /W₁的实际值计算出来。

用同样的方法可以得到与时间相关的轨迹特征消耗能量U、最大速度v _max和最大加速度a _max以及权重比W₃ /W₁的权重调整关系式:

$\begin{matrix} F_{time} = q_{1} (W_{3} / W_{1})^{- α} (15) \end{matrix}$

其中指数 $\begin{matrix} - α 在一定的区域范围内是固定的, 常系数 q_{1} \end{matrix}$ 则是不断变化的。

距离障碍物最短距离与限值L _IM呈线性关系:

$\begin{matrix} d_{\min} = q_{2} L_{IM} (16) \end{matrix}$

q₂为常系数。式(15)(16)中的常系数q₁和q₂是用权重和特征值进行在线计算,系数和理想特征值被用来计算新的权重值。

三个权重W₃ /W₁,W₂ /W₁和L _IM的取值并不是完全独立的,应该考虑各个权重之间的相对关系,以生成综合考虑各项评价指标的最优行驶轨迹。例如,当L _IM的值降低时,轨迹可以同时获得较小的消耗能量和较短的运行时间,效果可能不明显,但是如果权重调整不能找到时间和消耗能量的最优值,则可采用改变L _IM的值来获得时间和消耗能量的最优值。通过综合考虑各个评价指标可以得出如表1所示的几个主要轨迹特征运行时间、距离障碍物最短距离和消耗能量的权重进行在线调整的规则。其他与时间以及距离相关的轨迹特征,如平均速度、平均加速度等约束条件不满足时,也按照同样的权重调整进行调整。权重调整的流程图如图5所示。根据权重调整规则和流程进行权重调整可以保证各项评价指标能够综合平衡,不出现矛盾和振荡现象。

表1 权重调整规则 Table 1 The regulation rules of weight

	Figure Option View Download New Window
	图5 权重调整的流程图Fig.5 Flow chart of weight regulation

4 仿真结果与分析

针对车辆在障碍物环境中进行避障行驶的工况,用本文提出的基于最优控制理论的方法进行轨迹生成的仿真实验,以验证本文方法的有效性和可行性。本文对某型汽车进行仿真分析,该型汽车的相关配置参数如下:轴距为2.578 m,车身总长度为4.199 m,车身总宽度为1.786 m。障碍物集合 $\begin{matrix} {O} 定义为包括障碍物中心 (x, y) 和半径 r \end{matrix}$ 的集合。

$\begin{matrix} {O} = {{(16,4), 1}, {(5,8), 0.5}} \end{matrix}$

约束集合 L₀为:

$\begin{matrix} \begin{matrix} L_{0} = \\ {a_{\max} < 6.5, v_{\max} < 7.0, d_{\min} > 2.5, U \leq 60} \end{matrix} \end{matrix}$

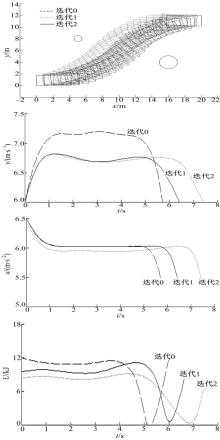
用本文方法进行轨迹参数优化的计算结果如表2所示。 D₀为初始估计权重以及对应的轨迹特征值, D₁和 D₂分别表示权重调整过程中每一步迭代计算的结果, $\begin{matrix} W_{i} (i = 0,1, 2) \end{matrix}$ 为三次权重调整的权重值。由表中计算结果可以看出,用本文权重调整方法得到的轨迹参数优化结果满足约束条件。

表2 用权重调整规则进行调整的迭代计算结果 Table 2 The iteration computed results using the weight regulation rules

通过不同迭代生成的权重对行驶轨迹、车速、加速度和消耗能量影响的仿真结果如图6所示,由图6(a)可以看出,通过迭代计算后的权重即迭代2生成的轨迹满足 d_min>2.5 m的约束条件,而用迭代0和迭代1的权重系数生成的轨迹不满足该约束条件,所以经过迭代计算后的权重系数可以生成满足约束条件的最优轨迹。由图6(b)可以看出,用迭代0生成的权重进行规划的最高车速没有满足 u_max<7.0 m/s的约束条件,迭代1和2都满足该约束条件。由图6(c)可以看出,用迭代0和1生成的权重进行规划的最大加速度没有满足 a_max<6.5 m/s²的约束条件,而用迭代2生成的权重进行规划的最高加速度满足该约束条件。由图6(d)可以看出,用迭代2生成的权重进行规划的消耗能量最低,满足 U≤60 kJ的约束条件。所以,使用本文提出的基于最优控制理论的方法生成的轨迹能够满足所有的约束条件,可以生成可行的最优轨迹。

	Figure Option View Download New Window
	图6 不同迭代生成的权重对行驶轨迹、车速、加速度和消耗能量影响的仿真结果Fig.6 Simulation results of different weights on driving trajectory,velocity,acceleration and energy

5 结论

(1)应用本文方法规划的行驶轨迹具有动态适用于不同道路环境的优点,能够保证车辆在不同的障碍物环境中顺畅地沿着规划轨迹行驶。

(2)本文方法考虑车辆消耗能量约束、最大加速度约束、最大速度约束和距离障碍物的最短距离约束对轨迹规划的影响,生成可行的行驶轨迹,使得车辆能够满足具体的行驶要求。

(3)仿真结果表明:本文提出的方法有效可行,可以迭代生成满足多个非完整约束条件的最优行驶轨迹。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Gharavi H, Prasad K V, Ioannou P. Scanning advanced automobile technology[J]. Proceedings of the IEEE, 2007, 95(2): 328-333. [本文引用:1] [JCR: 6.911]
[2]	Ren D B, Zhang J Y, Zhang J M, et al. Trajectory planning and yaw rate tracking control for lane changing of intelligent vehicle on curved road[J]. Science China (Technological Sciences), 2011, 54(3): 630-642. [本文引用:1]
[3]	宋金泽, 戴斌, 单恩忠, 等. 融合动力学约束的自主平行泊车轨迹生成方法[J]. 中南大学学报: 自然科学版, 2009, 40(增刊1): 135-141. Song Jin-ze, Dai Bin, Shan En-zhong, et al. Trajectory planning approach of autonomous parallel parking with kinodynamic constraints[J]. Journal of Central South University (Science and Technology), 2009, 40(Sup. 1): 135-141. [本文引用:1] [CJCR: 0.789]
[4]	Cheng P, Frazzoli E, LaValle S. Improving the performance of sampling-based motion planning with symmetry-based gap reduction[J]. IEEE Transactions on Robotics, 2008, 24(2): 488-494. [本文引用:1] [JCR: 2.571]
[5]	沈峘, 凌锐, 李舜酩. 考虑轮胎无滑移的智能车辆连续曲率轨迹规划方法[J]. 中国机械工程, 2012, 23(18): 2263-2267. Shen Huan, Ling Rui, Li Shen-ming. Continuous curvature trajectory planning method for intelligent vehicle considering no slip constraints[J]. China Mechanical Engineering, 2012, 23(18): 2263-2267. [本文引用:1] [CJCR: 0.751]
[6]	Muller B, Deutscher J, Grodde S. Continuous curvature trajectory design and feedforward control for parking a car[J]. IEEE Transactions on Control Systems Technology, 2007, 15(3): 541-553. [本文引用:1] [JCR: 2.0]
[7]	毛征宇, 刘中坚. 一种三次均匀B样条曲线的轨迹规划方法[J]. 中国机械工程, 2010, 21(21): 2569-2572, 2577. Mao Zheng-yu, Liu Zhong-jian. A trajectory planning method for cubic uniform B-spline curve[J]. China Mechanical Engineering, 2010, 21(21): 2569-2572, 2577. [本文引用:1] [CJCR: 0.751]
[8]	魏庆来. 基于近似动态规划的非线性系统最优控制研究[D]. 沈阳: 东北大学, 2009. Wei Qing-lai. Researches on optimal control of nonlinear systems based on approximate dynamic programming[D]. Shenyang: Northeastern University, 2009. [本文引用:1]
[9]	高兴泉, 马苗苗, 陈虹. 考虑时域硬约束的T-S模糊系统最优控制[J]. 吉林大学学报: 工学版, 2007, 37(3): 640-645. Gao Xing-quan, Ma Miao-miao, Chen Hong. Optimal control for T-S fuzzy systems with time domain hard constraints[J]. Journal of Jilin University(Engineering and Technology Edition), 2007, 37(3): 640-645. [本文引用:1] [CJCR: 0.701]
[10]	Dib W, Serrao L, Sciarretta A. Optimal control to minimize trip time and energy consumption in electric vehicles[C]∥IEEE Vehicle Power and Propulsion Conference, Chicago, IL, USA, 2011: 1-8. [本文引用:1]

2007

6.911

0.0

... 0 引言智能车辆是智能交通系统的重要组成部分,国际上众多的研究机构及工业设计单位对其研发过程正投入大量的人力、物力,时刻关注着关键技术的研发^[1,2] ...

2011

0.0

. 2011, 54(3):630-642 DOI:10.1007/s11431-010-4227-6

Trajectory planning and yaw rate tracking control for lane changing of intelligent vehicle on curved road

1. School of Automotive Engineering, Harbin Institute of Technology at Weihai, Weihai 264209, China; 2. State Key Laboratory of Traction Power, Southwest Jiaotong University, Chengdu 610031, China

The lateral control for lane changing of intelligent vehicle on curved road in automatic highway systems was studied. Based on trapezoidal acceleration profile, considering the curvature difference between starting lane and target lane, a new virtual trajectory planning method for lane changing on curved road was presented, and the calculating formulas for ideal states of vehicle in the inertial coordinate system during a lane changing maneuver were established. Applying the predetermined trajectory, the reference yaw angle and yaw rate for lane changing were generated. On the assumption that the information on yaw rate of vehicle can be measured with on-board sensors and based on the lateral dynamical model of vehicle, the yaw-rate-tracking control law was designed by applying nonsingular terminal sliding mode technology. Based on Lyapunov function method, the finite-time convergence property of the system was obtained from the phase-plane analysis. Simulation results showed that if the curvature difference between starting lane and target lane was not considered, then at the finishing time of lane changing, it was impossible to avoid the deviation of the virtual trajectory panned from the target lane, which increased with the decrease of curvature radius. With the trajectory planning method and yaw rate-tracking control law proposed in this paper and considering the curvature difference between the starting lane and target lane, the desired virtual trajectory for lane changing without deviation was obtained and the expected tracking performance was also verified by the simulation.

2009

0.0

0.789

... 轨迹规划技术是车辆进行自动行驶的一项关键技术^[3,4] ...

2008

2.571

0.0

... 轨迹规划技术是车辆进行自动行驶的一项关键技术^[3,4] ...

2012

0.0

0.751

... 轨迹规划的目的是要在适当的限制条件下,生成车辆运动轨迹的状态表达式,作为跟踪控制系统的控制输入^[5] ...

2007

2.0

0.0

... 早期的轨迹规划方法主要是用不同的函数(例如 B样条函数,多项式函数,正弦函数以及圆弧等)来模拟轨迹,并对车辆这一非线性系统施加多种约束条件,在约束条件范围内求解可行的轨迹^[6,7] ...

2010

0.0

0.751

2009

0.0

... 最优控制方法主要对评价函数施加不同的约束条件从而求出最优轨迹,但是最优控制方法中由于评价函数的权重不能实现在线调整,所以规划的轨迹也不能动态适应变化的道路环境^[8,9] ...

2007

0.0

0.701

. 2007, 37(3):640-645

Optimal control for T-S fuzzy systems with time domain hard constraints

1.College of Communication Engineering, Jilin University,Changchun 130022,China; 2.Jilin Institute of Chemical Technology, Jilin 132022, China

An optimal control algorithm for T-S fuzzy systems with time domain hard constraints including control input constraints and state constraints was proposed, in which the output energy was chosen as performance function with the initial state under a bound. This algorithm was realized by minimizing the invariant ellipsoid of the closed loop system. Some sufficient conditions dependent on the invariant set for the satisfaction of the time domain hard constraints were also derived. The multi-objective design was finally deduced to solve an optimization problem with a set of nonlinear matrix inequalities. The solution for this problem was given, and the feasibility of this scheme was discussed. Simulation results for the application in inverted pendulum validate this control algorithm.

针对带有时域硬约束（控制输入约束和状态约束）的T-S模糊系统，提出了一种基于状态反馈的优化控制算法。在系统初始状态小于某个界的情况下，将性能输出的能量作为优化的性能指标，通过最小化系统的不变椭圆域来实现系统优化控制，同时得到依赖于该不变域的满足时域硬约束的充分条件。该多目标控制问题最后归结为求解在一组非线性不等式约束条件下的优化问题，本文给出了该优化问题的解决方法，并分析了该方法的可行性。在倒立摆系统中应用的仿真结果验证了该方法的有效性。

2011

0.0

... 1 多目标动态评价函数运用最优控制方法进行轨迹规划,其目的是求出可用的控制输入变量 u(t)*,使得以微分方程描述的系统式(1)能够沿着可行的最小化评价函数(2)的轨迹x(t)*进行循迹行驶^[10] ...