欠驱动半挂汽车列车的运动建模与跟踪控制

引用本文

游峰, 张荣辉, 王海玮, 徐建闽, 温惠英. 欠驱动半挂汽车列车的运动建模与跟踪控制. 吉林大学学报:工学版, 2014, 44(5): 1296-1302[YOU Feng, ZHANG Rong-hui, WANG Hai-wei, XU Jian-min, WEN Hui-ying. Dynamic model and tracking control of tractor semi-trailer vehicle with underactuated system. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1296-1302] 复制到剪切板

Permissions

欠驱动半挂汽车列车的运动建模与跟踪控制

游峰¹, 张荣辉², 王海玮¹, 徐建闽¹, 温惠英¹

1.华南理工大学土木与交通学院, 广州 510640

2.中国科学院新疆理化技术研究所, 乌鲁木齐 830011

通信作者:张荣辉(1981-),男,副研究员,博士.研究方向:交通信息与安全,智能车辆.E-mail:zhangrh@ms.xjb.ac.cn

作者简介:游峰(1977-),男,副教授,博士.研究方向:车路协同与安全控制.E-mail:youfeng77@126.com

基金:国家自然科学基金项目(11147128,51108192,51208500); 中国博士后科学基金项目（2012M521824,2013T60904）; 乌鲁木齐市科技攻关计划项目（G121310001）; 中央高校基本科研业务费专项基金项目(x2tjD2115990)

摘要

应用车辆系统动力学理论,建立了以车辆参考坐标系和地面坐标系的欠驱动汽车列车动态模型。为了简化验算和求解过程,采用准确线性化方法对建立的系统模型进行线性化。在此基础上,针对小曲率转弯半径的车辆运行轨迹,建立了极坐标下的汽车挂车系统运动学模型,应用滑模变结构控制理论,给出了车辆系统状态变量向超平面收敛的方法。最后,对平滑运动轨迹和小曲率转弯半径的跟踪控制进行了仿真分析。仿真实验结果表明:所设计的反馈控制器能改善汽车列车对行驶路线的跟踪能力,使偏离的车辆快速返回到期望的稳态轨迹上。

关键词: 交通运输工程; 车辆动力学; 欠驱动系统; 半挂汽车列车; 滑模变结构控制

中图分类号:U461 文献标志码:A 文章编号:1671-5497(2014)05-1296-07

Dynamic model and tracking control of tractor semi-trailer vehicle with underactuated system

YOU Feng¹, ZHANG Rong-hui², WANG Hai-wei¹, XU Jian-min¹, WEN Hui-ying¹

1.School of Civil Engineering and Transportation, South China University of Technology, Guangzhou 510640, China

2.Xinjiang Technical Institute of Physics & Chemistry, Chinese Academy of Sciences, Urumqi 830011, China

Abstract

The dynamic theory of vehicle system is applied to develop the nonlinear dynamic model of underactuated vehicle in the vehicle and ground coordinate system. To simplify the process of checking and solving, the proposed model is linearized using accurate linearization method. On the basis of the linearized model, the dynamic model of tractor trailer system in polar coordinate system is established for vehicle trajectory in small turning curvature. In addition, the algorithm based on variable structure sliding model control is employed to make the state vectors of the vehicle system to converge to the hyperplane. Finally, the tracking simulations for smooth trajectory and smaller turning radius trajectory are analyzed in detail. Experiment results reveal that the designed feedback controller can improve the tracking performance of the tractor semi-trailer vehicle and drive the deviated vehicle back to the desired trajectory.

Keyword: engineering of communications and transportation; vehicle dynamics; underactuated system; semi-trailer vehicle; sliding mode variable structure control

Show Figures

0 引言

半挂汽车列车具有载重量大、纵向尺寸长、整车质心高等特点,与其他公路车辆相比,其侧滑极限较低,易出现偏离行驶车道或期望路径的现象,而驾驶员位于牵引车前方的驾驶室内,很难察觉事故的发生^{[ 1]}。半挂汽车列车是本身存在一定运动约束的一类欠驱动物理系统,即独立控制输入少于自由度的系统^{[ 2]}。加之半挂汽车列车系统具有运输效能高、成本低等优点,因此引起汽车工业界和学术界的广泛关注。刘宏飞^{[ 3]}应用车辆动力学原理建立汽车列车横向稳定性数学模型,研究汽车列车横向摆振产生机理,探索汽车列车使用参数和结构参数对其行驶稳定性的影响。周淑文等^{[ 4]}分析了半挂汽车列车转向特点,建立了半挂汽车列车多体动力学模型,采用虚拟样机技术,对横摆角速度跟踪控制和防倾覆控制进行仿真。常胜等^{[ 5]}建立四轮转向半挂汽车列车简化三自由度单轨动力学模型,在小角度转向和直线行驶两种行驶工况下对操纵稳定性能进行时域仿真研究。王云鹏等^{[ 6]}针对运输液态危险化学品的罐式半挂汽车列车,建立了整车侧倾数学模型,通过对移线和转向典型工况下整车动力学仿真,分析了变装载条件、变车速条件下车辆发生侧翻的规律。在文献[7]中,杨秀建等分析了牵引点和挂车质心位置对半挂汽车列车横向稳定性的影响规律,采用主元特征向量分析方法探讨半挂汽车列车“折叠”和“横向摆振”发生机理。

以上研究大都建立了不同类型的汽车列车的运动学和动力学模型,为汽车列车的深入研究奠定了基础,但如何保证挂车与牵引车沿一定轨迹行驶,尤其在小曲率半径轨迹条件下预定轨迹的跟踪,仍需进一步探讨和分析。为此,本文首先针对一类欠驱动汽车挂车系统的运动展开分析,在车辆运动假设的基础上,建立了车辆的微分动力学模型用以保证车辆直线跟踪性能。为简化验算和求解过程,应用准确线性化方法对建立的系统模型进行线性化。在此基础上,针对在小曲率半径情况下,欠驱动汽车挂车系统的侧滑极限降低^{[ 8]},侧滑概率进一步增加的情况建立极坐标下的系统运动学模型。最后应用基于滑模变结构方法设计了欠驱动汽车挂车系统的跟踪控制算法,通过仿真试验手段分析和验证了控制算法的有效性和实时性。

1 欠驱动汽车挂车的运动建模

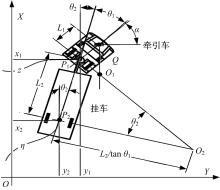建立如图1所示的坐标系统^{[ 3]},其中 $\begin{matrix} (XOY) \end{matrix}$ 为笛卡尔坐标系,用以代表汽车挂车的位置。图中各符号具体含义如表1所示。

	Figure Option View Download New Window
	图1 欠驱动汽车挂车运动模型Fig.1 Dynamics model of tractor semi-trailer vehicle with characteristics of underactuated system

表1 欠驱动汽车挂车建模参数的定义 Table 1 Parameter definition of tractor semi-trailer vehicle

1.1 欠驱动汽车挂车动态特性分析

假定欠驱动汽车的牵引车辆和挂车运行在同一个平面;车辆低速运行,车轮未发生侧滑。为便于研究,牵引车采用简化的三轮车模型,如图1所示。牵引车与挂车的铰接点为 $\begin{matrix} P_{1} \end{matrix}$ 。分析图中几何关系可知,欠驱动汽车挂车动态特性的微分方程如下:

$\begin{matrix} \begin{matrix} \frac{d}{dz} (θ_{1} + θ_{2}) = \frac{1}{L_{1}} tanα (1) \\ d θ_{2} / dη = \tan θ_{1} / L_{2} (2) \\ \frac{d x_{2}}{dη} = \cos θ_{2} (3) \\ \frac{d y_{2}}{dη} = \sin θ_{2} (4) \\ \frac{dη}{dz} = \cos θ_{1} (5) \end{matrix} \end{matrix}$

分析上述各式可知,式(1)描述了牵引车辆的运动特性;式(2)(3)(4)代表挂车的运动特性;式(5)为牵引车和挂车间运行轨迹的关系。

引入新的时间函数 $\begin{matrix} x_{2}, \end{matrix}$ 定义为挂车与期望运行轨迹间的距离。新量标 $\begin{matrix} x_{2} \end{matrix}$ 与时间 $\begin{matrix} t \end{matrix}$ 的关系为:

$\begin{matrix} \frac{d x_{2}}{dt} = \cos θ_{2} \cos θ_{1} \overset{\cdot}{z} (6) \end{matrix}$

式中: $\begin{matrix} \overset{\cdot}{z} \end{matrix}$ 为牵引车的速度。

如果 $\begin{matrix} θ_{1} \in (- \frac{π}{2}, \frac{π}{2}), θ_{2} \in (- \frac{π}{2}, \frac{π}{2}) \end{matrix}$ 且 $\begin{matrix} \overset{\cdot}{z} > 0, 则 x_{2} \end{matrix}$ 是关于时间 $\begin{matrix} t \end{matrix}$ 的严格单调递增函数。

结合式(1)~(5)整理有:

$\begin{matrix} \begin{matrix} \frac{d}{d x_{2}} (\begin{matrix} y_{2} \\ θ_{1} \\ θ_{2} \end{matrix}) = (\begin{matrix} \tan θ_{2} \\ - \frac{\tan θ_{1}}{L_{2} \cos θ_{2}} \\ \frac{\tan θ_{1}}{L_{2} \cos θ_{2}} \end{matrix}) + \\ (\begin{matrix} 0 \\ \frac{1}{L_{1} \cos θ_{1} \cos θ_{2}} \\ 0 \end{matrix}) tanα (7) \end{matrix} \end{matrix}$

1.2 非线性系统准确线性化方法

Su^{[ 9]}和Krener^{[ 10]}提出非线性系统准确线性化的方法,本文借鉴相关方法对欠驱动汽车挂车运动展开研究,并基于此设计相应的轨迹跟踪控制器。对于描述非线性系统的状态方程:

$\begin{matrix} \frac{dx}{dt} = f (x) + g (x) u (8) \end{matrix}$

设法找到一个坐标变换和非线性反馈:

$\begin{matrix} \{\begin{matrix} ξ = T (x) \\ u = α (x) + β (x) v \end{matrix} (9) \end{matrix}$

结合式(8)(9)可得到一个新的状态方程:

$\begin{matrix} \frac{dξ}{dt} = \end{matrix} \frac{\partial ξ}{\partial x} \frac{dx}{dt} (10)$

整理后有：

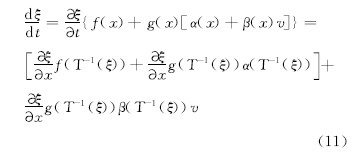
如果这个系统是线性的,即:

$\begin{matrix} \frac{dξ}{dt} = Aξ + Bv (12) \end{matrix}$

则式(7)描述的系统被转化成线性系统。而跟踪控制器可应用传统的线性控制理论来进行设计。由此可知,只要坐标变换式(8)和非线性反馈式(9)存在,就可以寻找到一个控制器,使得系统在初始状态的小范围内和大范围内都能保证系统的闭环稳定性。

1.3 欠驱动汽车挂车系统的准确线性化

为建立状态方程分析汽车挂车系统,本文引入新的状态变量和状态反馈:

$\begin{matrix} \begin{matrix} ξ = [\begin{matrix} ξ_{1} \\ ξ_{2} \\ ξ_{3} \end{matrix}] = [\begin{matrix} y_{2} \\ \tan θ_{2} \\ \tan θ_{1} / (L_{2} co s^{3} θ_{2}) \end{matrix}] (13) \\ tanα = \\ ta n^{- 1} \{- L_{1} \cos θ_{1} [3 si n^{3} θ_{1} \tan θ_{2} - \tan θ_{1}] / L_{2} + \\ L_{1} L_{2} co s^{3} θ_{1} co s^{4} θ_{2} v} (14) \end{matrix} \end{matrix}$

式中: $\begin{matrix} v \end{matrix}$ 为系统的新输入。

将 $\begin{matrix} ξ_{1} 、 ξ_{2} 、 ξ_{3} \end{matrix}$ 对 $\begin{matrix} x_{2} \end{matrix}$ 求导可知,通过引入新的状态变量 $\begin{matrix} ξ \end{matrix}$ 和新输入 $\begin{matrix} v, \end{matrix}$ 汽车挂车系统的非线性状态模型可实现准确的线性化:

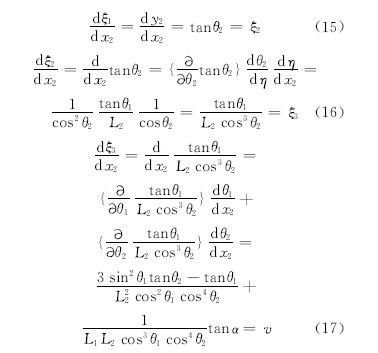
将式(15)(16)(17)重写,用如下状态方程表示为:

$\begin{matrix} \frac{dξ}{d x_{2}} = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{matrix}] ξ + [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}] v (18) \end{matrix}$

应用控制原理^{[ 11]}可以设计如下反馈控制器:

$\begin{matrix} v = [\begin{matrix} f_{1} & f_{2} & f_{3} \end{matrix}] {[\begin{matrix} ξ_{1} & ξ_{2} & ξ_{3} \end{matrix}]}^{T} (19) \end{matrix}$

根据式(13)(14)计算出牵引车前轮转角 $\begin{matrix} α : \end{matrix}$

$\begin{matrix} \begin{matrix} α = ta n^{- 1} [- L_{1} \cos θ_{1} (3 si n^{2} θ_{1} \tan θ_{2} - \\ \tan θ_{1}) / L_{2} + L_{1} L_{2} co s^{3} θ_{1} co s^{4} θ_{2} v] \\ (20) \\ v = f_{1} y_{2} + f_{2} \tan θ_{2} + f_{3} \frac{\tan θ_{1}}{L_{3} co s^{3} θ_{2}} \\ (21) \end{matrix} \end{matrix}$

分析式(21)可以得出以下结论:牵引车前轮转角 $\begin{matrix} α \end{matrix}$ 取决于 $\begin{matrix} y_{2} 、 θ_{1} 、 θ_{2} \end{matrix}$ 的取值,而 $\begin{matrix} v \end{matrix}$ 作为新的系统输入,是关于牵引车前轮转角 $\begin{matrix} α \end{matrix}$ 的函数。具体而言,当 $\begin{matrix} x_{2} \to \infty \end{matrix}$ 时, $\begin{matrix} ξ \to 0 \end{matrix}$ ,新引入的反馈式(19)使欠驱动汽车挂车系统式(18)稳定。随着时间标量 $\begin{matrix} x_{2} \end{matrix}$ 的增加, $\begin{matrix} y_{2} \to 0, θ_{1} \to 0, θ_{2} \to 0 。 \end{matrix}$ 考虑到 $\begin{matrix} x_{2} \end{matrix}$ 单调递增,即 $\begin{matrix} \overset{\cdot}{ξ} > 0 \end{matrix}$ ,当牵引车和挂车正常行驶时, $\begin{matrix} θ_{1} \in (- π / 2, π / 2), θ_{2} \in (- π / 2, π / 2), y \in (- \infty, \infty) \end{matrix}$ 始终限定于这些范围,因此欠驱动汽车挂车系统将跟踪 $\begin{matrix} X \end{matrix}$ 轴。

2 小曲率转弯半径的汽车挂车系统运动分析

在小曲率半径条件下,即 $\begin{matrix} R < 2 (L_{1} + L_{2}), \end{matrix}$ 欠驱动汽车挂车系统的侧滑极限降低^{[ 12]},侧滑概率进一步增加。

如图2所示,将小曲率半径的运行路径用圆形近似代替,文中选用极坐标 $\begin{matrix} (γ, φ) \end{matrix}$ 表示挂车系统,原点是期望运行路径的运动中心。期望圆弧的半径是 $\begin{matrix} R \end{matrix}$ 。选取弧长 $\begin{matrix} l = Rφ \end{matrix}$ 作为新的时间函数,因此可用极坐标形式描述欠驱动汽车挂车系统的动态特性。

	Figure Option View Download New Window
	图2 小曲率转弯半径的欠驱动汽车挂车运动模型Fig.2 Dynamic model of the vehicle in small turning radius of curvature

$\begin{matrix} \begin{matrix} \frac{d}{dt} (\begin{matrix} r - R \\ θ_{1} \\ θ_{2} - φ \end{matrix}) = (\begin{matrix} \frac{rcot (θ_{2} - φ)}{R} \\ - \frac{rtan θ_{1}}{R L_{2} \sin (θ_{2} - φ)} \\ \frac{rtan θ_{1}}{R L_{2} \sin (θ_{2} - φ)} - \frac{1}{R} \end{matrix}) + \\ (\begin{matrix} 0 \\ \frac{r}{R L_{1} \cos θ_{1} \sin (θ_{2} - φ)} \\ 0 \end{matrix}) tanα (22) \end{matrix} \end{matrix}$

新的时间函数 $\begin{matrix} l \end{matrix}$ 对时间的微分状态方程为:

$\begin{matrix} \begin{matrix} \frac{dl}{dt} = \frac{Rsin (θ_{2} - φ)}{r} \cos (θ_{1}) \overset{\cdot}{ξ} (23) \\ ξ = (\begin{matrix} ξ_{1} \\ ξ_{2} \\ ξ_{3} \end{matrix}) = \\ (\begin{matrix} r - R \\ \frac{rcos (θ_{2} - φ)}{R} \\ \frac{L_{2} {co s^{2} (θ_{2} - φ) + 1} rsin (θ_{2} - φ) - r^{2} \tan θ_{1}}{R^{2} L_{2} si n^{3} (θ_{2} - φ)} \end{matrix}) (24) \end{matrix} \end{matrix}$

本文引入新的状态变量和状态反馈:

$\begin{matrix} \begin{matrix} α = ta n^{- 1} {\frac{(co s^{2} δ + 5) L_{1} L_{2} cosδco s^{3} θ_{1} sinδ}{r^{2}} + \\ \frac{L_{1} \sin θ_{1}}{L_{2}} - \frac{9 L_{1} co s^{2} θ_{1} \sin θ_{1}}{r} + \\ \frac{3 L_{1} cosδcos θ_{1} si n^{2} θ_{1}}{L_{2} sinδ} - \\ \frac{R^{3} L_{1} L_{2} co s^{3} θ_{1} si n^{4} δ}{r^{3}} v} (25) \end{matrix} \end{matrix}$

令 $\begin{matrix} δ = θ_{2} - φ; v \end{matrix}$ 为当前情况下引入的新输入,此时系统线性化的状态方程与式(18)类似,但引入的状态变量和状态反馈为:

$\begin{matrix} \frac{dξ}{dt} = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{matrix}] ξ + [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}] v (26) \end{matrix}$

设计一个控制器,当汽车挂车向前行进时,选用的时间函数 $\begin{matrix} l \end{matrix}$ 不断增加,可使 $\begin{matrix} \forall ξ \to 0, 即 r \to R, \end{matrix}$ 可认为汽车挂车实现了对小曲率半径圆弧的跟踪。

3 基于滑模变结构的跟踪控制算法设计

欠驱动汽车挂车系统具有明显的非线性特性,而前述的准确线性化方法为应用反馈线性化控制算法提供了基础。本文采用基于滑模变结构^{[ 13, 14]}的方法设计欠驱动汽车挂车系统的跟踪控制算法。

设有线性时不变系统:

$\begin{matrix} {\overset{\cdot}{x}}_{a} = A x_{a} + Bu (27) \end{matrix}$

式中: $\begin{matrix} x_{a} \in R^{n}; u \in R^{m}; (A, B) \end{matrix}$ 为可控对偶阵。

系统对应的切换超平面为:

$\begin{matrix} S (X) = CX (28) \end{matrix}$

假设输入矩阵可分解为:

$\begin{matrix} B = [\begin{matrix} B_{1} \\ B_{2} \end{matrix}], \det B_{2} \neq 0 (29) \end{matrix}$

式中: $\begin{matrix} B_{1} \in R^{n - m}; B_{2} \in R^{m} 。 \end{matrix}$

选择坐标变换:

$\begin{matrix} \begin{matrix} x_{a} = Tx (30) \\ T = [\begin{matrix} I_{n - m} & - B_{1} B_{2}^{- 1} \\ 0 & I_{m} \end{matrix}], detT \neq 0 (31) \\ 由此可得 : \\ x = T^{- 1} [\begin{matrix} x_{a 1} \\ x_{a 2} \end{matrix}] (32) \\ \{\begin{matrix} \overset{\cdot}{x} = T^{- 1} ATx + T^{- 1} Bu \\ S = C_{a} Tx \end{matrix} (33) \end{matrix} \end{matrix}$

式中: $\begin{matrix} x_{a 1} \in R^{n - m}; x_{a 2} \in R^{m} 。 \end{matrix}$

$\begin{matrix} \begin{matrix} T^{- 1} AT = [\begin{matrix} A_{11} & A_{12} \\ A_{21} & A_{22} \end{matrix}] (34) \\ T^{- 1} B = [\begin{matrix} 0 \\ B_{2} \end{matrix}] (35) \\ C_{a} T = [\begin{matrix} C_{1} & C_{2} \end{matrix}] (36) \end{matrix} \end{matrix}$

由此,可以得到下列规范系统的表达形式:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{1} = A_{11} x_{1} + A_{12} x_{2} \\ {\overset{\cdot}{x}}_{2} = A_{21} x_{1} + A_{22} x_{2} + B_{2} u \\ S = C_{1} x_{1} + C_{2} x_{2} \end{matrix} (37) \end{matrix}$

为求出汽车挂车系统进入滑模状态后变动最小的切换超平面,给出如下的最优评价函数:

$\begin{matrix} J = \int_{t_{s}}^{t} x^{T} Qxdt (38) \end{matrix}$

式中: $\begin{matrix} t_{s} \end{matrix}$ 为状态进入切换超平面的时刻。

$\begin{matrix} \begin{matrix} Q = [\begin{matrix} Q_{11} & Q_{12} \\ Q_{21} & Q_{22} \end{matrix}] (39) \\ {Q^{T}}_{21} = Q_{12}, Q > 0 (40) \end{matrix} \end{matrix}$

此时,式(38)可改写为:

$\begin{matrix} J = \int_{t_{s}}^{t} ({x^{T}}_{1} Q_{11} x_{1} + 2 {x^{T}}_{1} Q_{12} x_{2} + {x^{T}}_{2} Q_{22} x_{2} dt) (41) \end{matrix}$

取 $\begin{matrix} Q_{12} = 0, \end{matrix}$ 有:

$\begin{matrix} P A_{11} + {A^{T}}_{11} P - P A_{12} Q_{22}^{- 1} A_{12} P + Q_{11} = 0 (42) \end{matrix}$

$\begin{matrix} P \end{matrix}$ 是代数黎卡提(Riccati)方程的对称正定常数解,则使性能指标最小的最优控制为:

$\begin{matrix} \begin{matrix} x_{2} = - Q_{22}^{- 1} {A^{T}}_{12} P x_{1} (43) \\ 因此 : S (X) = [C_{a} C_{b}] X (44) \end{matrix} \end{matrix}$

式中: $\begin{matrix} C_{a} = {A^{T}}_{12} P; C_{b} = Q_{22} 。 \end{matrix}$

为使欠驱动汽车挂车系统状态从超平面之外向超平面收敛,并保持在该平面上,文中应用加速度型达到律改善收敛的动态品质,其优良特性表现为当系统状态远离滑模超平面时,状态收敛速度快,从而缩短收敛时间;而当状态靠近滑模超平面时,收敛速度变慢,减少控制系统的振荡。加速度型达到率^{[ 15]}的表达式为:

$\begin{matrix} \overset{\cdot}{S} = - G {|S|}^{α} sgn (S) (45) \end{matrix}$

由于 $\begin{matrix} \overset{\cdot}{S} = C \overset{\cdot}{X} = C (AX + BU) = - G {|S|}^{α} sgn (S), \end{matrix}$ 则可控制器的输出为:

$\begin{matrix} u = r - {(CB)}^{- 1} {CAX + G {|S|}^{α} sgn (S)} (46) \end{matrix}$

4 跟踪控制的仿真实验分析

为验证文中提出的滑模变结构控制算法的有效性,在Matlab\Simulink环境,结合Adams软件,建立如图3所示的仿真场景,对参考轨迹进行了计算机仿真跟踪实验。车辆相关参数选用一汽生产的解放牌CA9400CCY型仓栅式半挂车。

	Figure Option View Download New Window
	图3 基于Matlab/Adams的仿真软件Fig.3 Simulation software based on Matlab/Adams platform

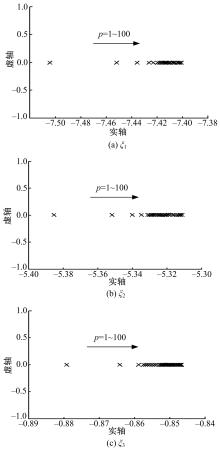
系统响应的速度和平稳性对于欠驱动汽车挂车控制系统而言都是至关重要的,故加权矩阵的选取要在兼顾系统响应速度的同时,还应考虑系统收敛的平稳性,使系统高速收敛、低振荡。结合式(41),选取 $\begin{matrix} Q_{11} \end{matrix}$ 为非负定的二阶常数矩阵, $\begin{matrix} Q_{22} \end{matrix}$ 为正常数。为便于讨论,将矩阵元素均设为1,给整个 $\begin{matrix} Q_{11} \end{matrix}$ 阵乘以权重系数 $\begin{matrix} p \end{matrix}$ ,使得:

$\begin{matrix} Q_{11} = p [\begin{matrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{matrix}]; Q_{22} = 1 (47) \end{matrix}$

图4为系统的状态变量 $\begin{matrix} ξ_{1} 、 ξ_{2} 、 ξ_{3} \end{matrix}$ 闭环极点在 $\begin{matrix} s \end{matrix}$ 平面上随 $\begin{matrix} p \end{matrix}$ 的变化轨迹。从图中可知,随着 $\begin{matrix} p \end{matrix}$ 的增大,系统状态所对应的极点均处于负半平面。

	Figure Option View Download New Window
	图4 ξ₁、 ξ₂、 ξ₃在 s平面上随 p变化的轨迹Fig.4 Trajectory of ξ₁、 ξ₂、 ξ₃ with the changing of p in s plane

4.1 平滑运动轨迹跟踪控制仿真

在平滑运动轨迹情况下,本文针对一类欠驱动汽车挂车系统进行仿真分析,仿真初始参数如下:

$\begin{matrix} ξ_{1} = y_{2}; ξ_{2} = \tan θ_{2} \end{matrix}$ ;

$\begin{matrix} ξ_{3} = \tan θ_{1} / {(L_{2} \cos θ_{2})}^{3} \end{matrix}$ ;

$\begin{matrix} y_{2} = 0.25 m; θ_{1} = θ_{2} = π / 10 \end{matrix}$ ;

$\begin{matrix} L_{1} = 4 m; L_{2} = 13 m 。 \end{matrix}$

从图5的仿真曲线可知,准确线性化系统的状态变量经过较短时间均收敛到0,由此可见设计的控制器可对平滑运动轨迹进行跟踪。

	Figure Option View Download New Window
	图5 平滑运动轨迹的跟踪控制仿真图Fig.5 Simulation figure of tracking control for smooth trajectory

4.2 小曲率转弯半径轨迹跟踪控制仿真

在小曲率半径轨迹条件下进行仿真分析的初始参数如下:

$\begin{matrix} ξ_{1} = r - R \end{matrix}$ ; $\begin{matrix} ξ_{2} = rcos (θ_{2} - φ) / R \end{matrix}$ ;

$\begin{matrix} ξ_{3} = \frac{L_{2} {co s^{2} (θ_{2} - φ) + 1} rsin (θ_{2} - φ) - r^{2} \tan θ_{1}}{R^{2} L_{2} si n^{3} (θ_{2} - φ)} \end{matrix}$ ;

$\begin{matrix} r = 21 m; R = 20 m; θ_{1} = π / 6; θ_{2} = π / 3; \end{matrix}$

$\begin{matrix} φ = π / 7; L_{1} = 4 m; L_{2} = 13 m; \end{matrix}$

$\begin{matrix} X_{0} = [\begin{matrix} ξ_{1} & ξ_{2} & ξ_{3} \end{matrix}] 。 \end{matrix}$

从图6的仿真曲线可知,准确线性化系统的状态变量经过较短时间均收敛到 $\begin{matrix} 0 \end{matrix}$ ,因此设计的控制器可对小曲率转弯半径轨迹进行跟踪。

	Figure Option View Download New Window
	图6 小曲率转弯半径轨迹的跟踪控制仿真图Fig.6 Simulation figure of tracking control for small turning radius

5 结束语

应用非线性动力学相关理论,对欠驱动汽车挂车系统动态机制和规律进行了分析,旨在为系统跟踪预定的路径和稳定性控制提供依据。针对一类欠驱动汽车挂车系统的运动特性展开分析,在车辆运动假设的基础上,建立了车辆的微分动力学模型。为简化验算和求解过程,应用准确线性化方法对建立的系统模型进行线性化。由于在小曲率半径条件下,一类欠驱动汽车挂车系统的侧滑极限降低,侧滑概率进一步增加,针对该种情况本文建立了极坐标下的系统运动学模型。应用基于滑模变结构方法设计一类欠驱动汽车挂车系统的跟踪控制算法,实验仿真分析验证了控制算法的有效性和实时性。本文为便于研究,忽略了轮胎侧滑特性的问题,在后续的研究中将结合轮胎的非线性模型进行半挂汽车列车跟踪控制的研究。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	宗长富, 朱天军, 郑宏宇, 等. 二次型最优控制的半挂汽车列车主动侧倾控制算法研究[J]. 中国机械工程, 2008, 19(7): 872-877. Zong Chang-fu, Zhu Tian-jun, Zheng Hong-yu, et al. Research on active roll control algorithm of heavy tractor semi-trailer based on LQG/LTR[J]. China Mechanical Engineering, 2008, 19(7): 872-877. [本文引用:1] [CJCR: 0.751]
[2]	孙宁, 方勇纯. 一类欠驱动系统的控制方法综述[J]. 智能系统学报, 2011, 6(3): 200-207. Sun Ning, Fang Yong-chun. A review for the control of a class of underactuated systems[J]. Transactions on Intelligent Systems, 2011, 6(3): 200-207. [本文引用:1]
[3]	刘宏飞. 半挂汽车列车横摆动力学仿真及控制策略研究[D]. 长春: 吉林大学汽车工程学院, 2005. Liu Hong-fei. Study on the simulation and control strategy for yaw motion dynamics of tractor-semi trailer[D]. Changchun: College of Automotive Engineering, Jilin University, 2005. [本文引用:2]
[4]	周淑文, 张思奇, 郭立新, 等. 半挂汽车列车高速紧急避障稳定性控制研究[J]. 汽车工程, 2009, 31(2): 161-165. Zhou Shu-wen, Zhang Si-qi, Guo Li-xin, et al. A study on stability control of semi-trailer combination for high speed obstacle avoidance under emergency[J]. Automotive Engineering, 2009, 31(2): 161-165. [本文引用:1] [CJCR: 0.618]
[5]	常胜, 许洪国, 刘宏飞. 四轮转向半挂汽车列车行驶稳定性仿真研究[J]. 计算机仿真, 2009, 26(12): 235-238. Chang Sheng, Xu Hong-guo, Liu Hong-fei. Steering stability simulation of 4WS tractor-semitrailer[J]. Computer Simulation, 2009, 26(12): 235-238. [本文引用:1] [CJCR: 0.5628]
[6]	王云鹏, 孙文财, 隗海林, 等. 基于侧倾的运输液态危险化学品的罐式半挂汽车危险状态辨识[J]. 吉林大学学报: 工学版, 2010, 40(3): 640-644. Wang Yun-peng, Sun Wen-cai, Kui Hai-lin, et al. Rollover risk of tractor semitrailer with liquid hazmat tank[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(3): 640-644. [本文引用:1] [CJCR: 0.701]
[7]	杨秀建, 李耀平, 熊坚. 半挂汽车列车横向稳定性与失稳机理分析[J]. 汽车工程, 2011, 33(6): 486-492. Yang Xiu-jian, Li Yao-ping, Xiong Jian. Analysis on the lateral stability and instability mechanism of tractor-semitrailer combination[J]. Automotive Engineering, 2011, 33(6): 486-492. [本文引用:1] [CJCR: 0.618]
[8]	李显生, 郑雪莲, 刘宏飞. 非满载罐式半挂汽车列车侧倾稳定性评价改进算法[J]. 吉林大学学报: 工学版, 2012, 42(5): 1089-1094. Li Xian-sheng, Zheng Xue-lian, Liu Hong-fei. Improved algorithm on roll stability evaluation of partially filled tractor-tank semitrailer[J]. Journal of Jilin University(Engineering and Technology Edition), 2012, 42(5): 1089-1094. [本文引用:1] [CJCR: 0.701]
[9]	Su R. On the linear equivalents of nonlinear systems[J]. Systems & Control Letters, 1982, 2(1): 48-52. [本文引用:1]
[10]	Krener A J. On the equivalence of control systems and the linearization of nonlinear systems[J]. SIAM Journal on Control, 1973, 11(4): 670-676. [本文引用:1] [JCR: 1.379]
[11]	Ellis G. Control System Design Guide: Using Your Computer to Understand and Diagnose Feedback Controllers[M]. Waltham, USA: Butterworth-Heinemann, 2012. [本文引用:1]
[12]	Deng W, Kang X. Parametric study on vehicle-trailer dynamics for stability control[J]. SAE Transactions, 2003, 112(6): 1411-1419. [本文引用:1]
[13]	Islam S, Liu X P. Robust sliding mode control for robot manipulators[J]. Industrial Electronics, IEEE Transactions on Industrial Electronics, 2011, 58(6): 2444-2453. [本文引用:1] [JCR: 5.165]
[14]	Wu L, Ho D W C, Li C W. Sliding mode control of switched hybrid systems with stochastic perturbation[J]. Systems & Control Letters, 2011, 60(8): 531-539. [本文引用:1]
[15]	Bhavsar P, Kumar V. Trajectory tracking of linear inverted pendulum using integral sliding mode control[J]. International Journal of Intelligent Systems and Applications (IJISA), 2012, 4(6): 31-35. [本文引用:1]

2008

0.0

0.751

. 2008, 19(7):872-877

Research on active roll control algorithm of heavy tractor semi-trailer based on LQG/LTR

针对半挂汽车列车的侧倾稳定性问题,建立了八自由度的半挂汽车列车动力学模型,并以线性二次型调节器(linear quadratic regulator,LQR)为基础,提出了一种基于回路传输恢复技术(loop transfer recovery,LTR)的线性二次型高斯(linear quadratic guass,LQG)最优控制算法.设计了局部状态反馈控制器,实现某车速下的侧倾控制,并进行了该车速下阶跃转向工况的车辆仿真分析.仿真结果表明:LQG/LTR控制器具有良好的抑制干扰噪声的能力和较好的鲁棒性,有效提高了半挂汽车列车的侧倾稳定性.

... 0 引言半挂汽车列车具有载重量大、纵向尺寸长、整车质心高等特点,与其他公路车辆相比,其侧滑极限较低,易出现偏离行驶车道或期望路径的现象,而驾驶员位于牵引车前方的驾驶室内,很难察觉事故的发生^[1] ...

2011

0.0

. 2011, 6(3):200-207

A review for the control of a class of underactuated systems

近年来欠驱动系统已经成为机器人与自动控制领域的研究热点之一,本文对一类欠驱动系统（欠驱动连杆系统）的控制方法的研究状况进行了综述.首先给出了欠驱动系统的动力学模型,并介绍了2种基本控制模式；随后,对其主要的控制方法,包括最优控制方法、运动规划法、部分反馈线性化方法、能量（无源)方法、变量降维法、分级控制设计方法及智能控制方法,展开了分析与讨论；在此基础之上,对欠驱动连杆控制系统设计存在的抗干扰性、实用性及快速性等主要问题进行了简要分析,并就今后的研究方向进行了展望,如鲁棒策略、饱和控制与有限时间控制等.

... 半挂汽车列车是本身存在一定运动约束的一类欠驱动物理系统,即独立控制输入少于自由度的系统^[2] ...

2005

0.0

... 刘宏飞^[3]应用车辆动力学原理建立汽车列车横向稳定性数学模型,研究汽车列车横向摆振产生机理,探索汽车列车使用参数和结构参数对其行驶稳定性的影响 ...

... 1 欠驱动汽车挂车的运动建模建立如图1所示的坐标系统^[3],其中 (XOY)为笛卡尔坐标系,用以代表汽车挂车的位置 ...

2009

0.0

0.618

. 2009, 31(2):161-165

A study on stability control of semi-trailer combination for high speed obstacle avoidance under emergency

分析了半挂汽车列车转向的特点,对其稳定性控制原理进行了研究,包括横摆角速度跟踪控制和防倾覆控制.在此基础上,建立了半挂汽车列车多体动力学模型,采用虚拟样机技术,对横摆角速度跟踪控制和防倾覆控制进行运动学与动力学仿真.结果表明,装用车辆动态控制系统后,提高了半挂汽车列车高速紧急避障时的操纵稳定性,因而,其避障行驶的极限条件大大宽松.

... 周淑文等^[4]分析了半挂汽车列车转向特点,建立了半挂汽车列车多体动力学模型,采用虚拟样机技术,对横摆角速度跟踪控制和防倾覆控制进行仿真 ...

2009

0.0

0.5628

. 2009, 26(12):235-238

Steering stability simulation of 4WS tractor-semitrailer

通过分析四轮转向(4WS)半挂汽车列车行驶性能,为在牵引车上采用4WS技术能提高整个汽车列车行驶稳定性提供依据.建立4WS半挂汽车列车简化三自由度单轨动力学模型,在小角度转向和直线行驶两种行驶工况下对操纵稳定性能进行时域仿真研究.理论分析和基于MATLAB的仿真研究表明,4WS技术能使车辆的横摆角速度等状态量保持较小数值.稳定性好.最后,与只有前轮转向(FWS)牵引车列车的稳定性能作对比分析,验证出4WS对列车的高速稳定性和低速机动性有明显的好处. Abstract： The purpose of this paper is to prove that the tractor adopting the four-wheel steering (4WS) can im-prove the tractor-semitrailer handling and stability through analyzing the performance of steering. A simplified single track model with 3 DOF for 4WS tractor-semitrailer has been constructed for the simulation of time domain under the conditions of small angle steering and longitudinal driving. The analysis and the simulation based on MATLAB show that this technique can keep the vehicle yawing velocity in a little scale. At last, the effect of 4WS is analyzed by comparing with front-wheel steering (FWS), and the study verifies that 4WS is beneficial to both the high-speed stability and low-speed flexibility of tractor-semitrailer.

... 常胜等^[5]建立四轮转向半挂汽车列车简化三自由度单轨动力学模型,在小角度转向和直线行驶两种行驶工况下对操纵稳定性能进行时域仿真研究 ...

2010

0.0

0.701

. 2010, 40(3):640-644

Rollover risk of tractor semitrailer with liquid hazmat tank

College of Transportation, Jilin University, Changchun 130022, China

Aiming at the tractor semitrailer with liquid hazmat tank, a mathematic model of vehicle rollover is built to reflect its movement response characteristics. Based on the real vehicle parameter, a dynamic simulation model of multibody vehicle is built in virtual environment of ADAMS. Through the dynamic simulation under two typical work conditionlanechanging and swerving, the rollover law is analyzed systematically under the condition of different vehicle speed and different load, the threshold values of the rollover of tractor semitrailer are gotten. The research conclusion is meaningful on the theoretical guide for the early warning of the risk during the running of the tractor semitrailer with liquid hazmat tank.

针对运输液态危险化学品的罐式半挂汽车列车，建立了用以反映其运动响应特性的整车侧倾数学模型；基于实车参数在ADAMS虚拟环境下建立了整车多体系统动力学模型；通过对移线和转向两种典型工况下整车动力学仿真，系统地分析了变装载条件、变车速条件下车辆发生侧翻的规律，得到了列车侧翻阈值。

... 王云鹏等^[6]针对运输液态危险化学品的罐式半挂汽车列车,建立了整车侧倾数学模型,通过对移线和转向典型工况下整车动力学仿真,分析了变装载条件、变车速条件下车辆发生侧翻的规律 ...

2011

0.0

0.618

. 2011, 33(6):486-492

Analysis on the lateral stability and instability mechanism of tractor-semitrailer combination

为半挂汽车列车建立了简化的四自由度单轨模型,并在其上分析了两个重要结构参数,即牵引点和挂车质心位置对半挂汽车列车横向稳定性的影响规律.在此基础上,采用主元特征向量分析方法详细探讨了半挂汽车列车"折叠"和"横向摆振"两种常见的横向失稳现象的发生机理,分析和对比了牵引角和牵引角速度输出反馈对半挂汽车列车"折叠"和"横向摆振"失稳的镇定效果.

2012

0.0

0.701

. 2012, 42(5):1089-1094

Improved algorithm on roll stability evaluation of partially filled tractor-tank semitrailer

College of Transportation, Jilin University, Changchun 130022, China

From the fact that the quasi-static method has deficiency in the solution of the transient mass center of sloshing fluid and the corresponding vehicle rollover modelling, the solutions of the transient mass center of sloshing fluid in tanks with modified square and modified oval cross sections were improved, and the exact equations for the mass center in the tank with modified square cross section were derived. A new vehicle rollover model was built without uncommon and hard-to-get parameters, simplifying the solution of vehicle rollover threshold. Using the improved quasi-static method, the change of the vehicle rollover threshold with filling percent under conditions of constant cargo density and constant cargo mass was simulated by Matlab. The results showed that the improved quasi-static method can predict accurately the vehicle rollover threshold.

针对传统准静态(QS)方法在瞬时液体质心的求解和车辆侧倾模型两方面存在的缺陷和不足,改进了改良的方形和椭圆形横截面罐体内瞬时液体质心的求解过程,并推导了改良方形罐体内液体质心的求解公式。重新建立了车辆侧倾模型,避免了不常见和难获得车辆参数的使用,简化了侧倾极限值的求解。利用改进的QS方法通过Matlab对液体密度固定和载质量固定两种情况下的车辆侧倾极限值随充液比的变化进行了仿真。仿真结果表明:改进的QS方法可准确地预测车辆侧倾极限值。

... 在此基础上,针对在小曲率半径情况下,欠驱动汽车挂车系统的侧滑极限降低^[8],侧滑概率进一步增加的情况建立极坐标下的系统运动学模型 ...

1982

0.0

... 2 非线性系统准确线性化方法Su^[9]和Krener^[10]提出非线性系统准确线性化的方法,本文借鉴相关方法对欠驱动汽车挂车运动展开研究,并基于此设计相应的轨迹跟踪控制器 ...

1973

1.379

0.0

2012

0.0

... 应用控制原理^[11]可以设计如下反馈控制器: ...

2003

0.0

... 2 小曲率转弯半径的汽车挂车系统运动分析在小曲率半径条件下,即 R2(L1+L2),欠驱动汽车挂车系统的侧滑极限降低^[12],侧滑概率进一步增加 ...

2011

5.165

0.0

... 本文采用基于滑模变结构^[13,14]的方法设计欠驱动汽车挂车系统的跟踪控制算法 ...

2011

0.0

. 2011, 60(8):531-539 DOI:10.1016/j.sysconle.2011.04.007

Sliding mode control of switched hybrid systems with stochastic perturbation

Abstract This paper is concerned with the sliding mode control (SMC) of a continuous-time switched stochastic system. A sufficient condition for the existence of reduced-order sliding mode dynamics is derived and an explicit parametrization of the desired sliding surface is also given. Then, a sliding mode controller is then synthesized for reaching motion. Moreover, the observer-based SMC problem is also investigated. Some sufficient conditions are established for the existence and the solvability of the desired observer and the observer-based sliding mode controller is synthesized. Finally, numerical examples are provided to illustrate the effectiveness of the proposed theory.

... 本文采用基于滑模变结构^[13,14]的方法设计欠驱动汽车挂车系统的跟踪控制算法 ...

2012

0.0

... 加速度型达到率^[15]的表达式为: ...