基于高斯Sigma点选取的改进UPF算法

引用本文

曹洁, 戴彬, 李晓旭. 基于高斯Sigma点选取的改进UPF算法. 吉林大学学报:工学版, 2014, 44(5): 1435-1440[CAO Jie, DAI Bin, LI Xiao-xu. Improved UPF algorithm based on Gaussian Sigma points selection. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1435-1440] 复制到剪切板

Permissions

基于高斯Sigma点选取的改进UPF算法

曹洁, 戴彬, 李晓旭

兰州理工大学计算机与通信学院, 兰州 730050

作者简介:曹洁（1966-）,女,教授,博士生导师.研究方向:信息融合理论与应用,智能交通,信息检测与估计. E-mail:caoj@lut.cn

基金:国家自然科学基金项目（61263031）

摘要

针对标准粒子滤波存在的粒子退化现象,提出了一种改进的UPF算法。该算法采用基于高斯Sigma点选取的自适应无味卡尔曼滤波产生建议分布函数,然后利用Metropolis-Hastings(MH)方法优化粒子,提高了对系统后验概率密度的逼近程度。仿真结果表明:改进算法降低了粒子滤波算法的粒子退化程度,提高了跟踪精度。

关键词: 计算机应用; 粒子滤波; 高斯Sigma点; 无味卡尔曼滤波; MH方法

中图分类号:TP391 文献标志码:A 文章编号:1671-5497(2014)05-1435-06

Improved UPF algorithm based on Gaussian Sigma points selection

CAO Jie, DAI Bin, LI Xiao-xu

College of Computer and Communication,Lanzhou University of Technology, Lanzhou 730050, China

Abstract

An improved Unscented Particle Filter (UPF) algorithm is proposed to overcome the problem of particles degradation in the standard particle filter. The algorithm uses adaptive unscented Kalman filter based on Gaussian Sigma point selection to generate the proposal distribution function. Then it uses the Metropolis-Hastings (MH) algorithm to optimize particles, so that the approximation of the posterior probability density of the system is improved. Simulation results show that the improved UPF algorithm reduces particle degradation which exists in the particle filter algorithm, and improves tracking accuracy.

Keyword: computer application; particle filter; Gaussian Sigma points; unscented Kalman filter; Metropolis-Hastings

Show Figures

0 引言

非线性、非高斯随机系统的状态估计问题在统计学、语音和图像处理、数字通信、计算机视觉、自适应估计、机器学习及自动控制等领域有着广泛应用^{[ 1]}。解决一般非线性状态估计问题常用Kalman滤波的相关改进算法,包括扩展Kalman滤波(EKF)^{[ 2]}、无味Kalman滤波(UKF)^{[ 3]}等。这些算法基本思想是通过参数化的解析式对系统的非线性进行近似来进行状态估计。但在许多非线性和非高斯条件下,这些滤波算法在估计系统状态时误差较大,可能导致滤波发散。近年来,粒子滤波^{[ 4]}被应用在解决非线性和非高斯系统状态估计问题上,但仍存在粒子退化现象。建议分布函数的选择是影响该问题一个重要因素,研究人员提出了很多基于建议分布函数选择的粒子滤波算法,其中有似然粒子滤波^{[ 5]}、扩展粒子滤波(EPF)^{[ 6]}、无味粒子滤波(UPF)^{[ 7]}和高斯-厄米粒子滤波^{[ 8]}等。其中UPF算法是目前被广泛应用的一种改进粒子滤波算法,但UPF算法的精度很大程度上取决于Sigma点的选取方式,现有的选取方式主要是对称选取,这种选取方式使Sigma点的采样点数过多,影响了算法的效率。

基于此,本文提出了一种改进的UPF算法。该算法采用高斯Sigma点选取的自适应无味卡尔曼滤波产生建议分布函数,然后利用MH方法^{[ 9]}优化粒子,提高了对系统后验概率密度的逼近程度。为了评估本文提出的改进算法的性能,选择两个仿真系统将其与PF、EPF和UPF三种算法进行了比较。

1 无味粒子滤波(UPF)

1.1 标准粒子滤波(PF)

粒子滤波是一种基于蒙特卡罗方法和递推贝叶斯估计的统计滤波方法。该方法核心思想是利用一系列随机样本的加权和来表示系统状态的后验概率密度,以样本均值代替积分计算,从而获得状态的最小方差估计。

假设非线性系统动态模型如下:

$\begin{matrix} \begin{matrix} 状态方程 : x_{k} = f (x_{k - 1}) + v_{k - 1} (1) \\ 量测方程 : z_{k} = h (x_{k}) + u_{k} (2) \end{matrix} \end{matrix}$

式中: $\begin{matrix} x_{k} \end{matrix}$ 为系统状态; $\begin{matrix} z_{k} \end{matrix}$ 为观测状态;映射 $\begin{matrix} f (\cdot) \end{matrix}$ 和 $\begin{matrix} h (\cdot) \end{matrix}$ 分别为系统状态转移模型函数和量测模型函数; $\begin{matrix} v_{k - 1} \end{matrix}$ 和 $\begin{matrix} u_{k} \end{matrix}$ 分别为过程噪声和观测噪声。

令 $\begin{matrix} {x_{k}^{i}, w_{k}^{i}, i = 1, \dots, N} \end{matrix}$ 表示一组加权随机样本(粒子),其中 $\begin{matrix} x_{k}^{i} \end{matrix}$ 为 $\begin{matrix} k \end{matrix}$ 时刻第 $\begin{matrix} i \end{matrix}$ 个粒子的状态, $\begin{matrix} w_{k}^{i} \end{matrix}$ 为 $\begin{matrix} x_{k}^{i} \end{matrix}$ 的权值,则 $\begin{matrix} k \end{matrix}$ 时刻后验概率密度为:

$\begin{matrix} p (x_{k} |z_{k}) = \overset{N}{\sum_{i = 1}} w_{k}^{i} δ (x - x_{k}^{i}) (3) \end{matrix}$

式中:粒子 $\begin{matrix} {x_{k}^{i}, i = 1, \dots, N} \end{matrix}$ 从建议分布函数 $\begin{matrix} q (x_{k}^{(i)} | x_{0 ∶ k - 1}^{(i)}, z_{1 ∶ k}) \end{matrix}$ 抽样,权值 $\begin{matrix} w_{k}^{i} \end{matrix}$ 通过重要采样法选择。

$\begin{matrix} w_{k}^{(i)} \propto w_{k - 1}^{(i)} \frac{p (z_{k} | x_{k}^{(i)}) p (x_{k}^{(i)} | x_{k - 1}^{(i)})}{q (x_{k}^{(i)} | x_{0 ∶ k - 1}^{(i)}, z_{1 ∶ k})} (4) \end{matrix}$

式(3)中: $\begin{matrix} δ (x - x_{k}^{i}) \end{matrix}$ 为单位冲激函数(狄拉克函数),即 $\begin{matrix} δ (x - x_{k}^{i}) = 0, x \neq x_{k}, \end{matrix}$ 且∫ δ( x)d x=1,权值满足归一化条件 $\begin{matrix} \overset{N}{\sum_{i = 1}} \end{matrix} \begin{matrix} w_{k}^{i} \end{matrix}$ =1。

1.2 无味粒子滤波(UPF)

UPF算法是UKF算法和PF算法的结合。在PF算法中,为了求解方便,一般取先验概率密度为建议分布函数。但是,这种选取方法丢失了当前时刻的量测值,使得当前时刻的状态严重依赖于模型。如果模型不准确,或者量测噪声突然增大,这种选取方法将不能有效地表示概率密度函数的真实分布,会产生很大的估计偏差。UPF算法则是在PF的基础上利用UKF产生建议分布函数,每一次采样的粒子集都由UKF算法进行更新,所得的均值和方差用于下一次采样新粒子集。在重要性采样环节引入最新的观测量,可以在一定程度上抑制粒子退化。

2 改进的UPF算法

2.1 基于高斯Sigma点选取的UKF算法

UKF是无味变换和标准Kalman滤波体系的结合。无味变换的基本思想是根据 $\begin{matrix} x \end{matrix}$ 的均值和方差选择 $\begin{matrix} 2 n_{x} + 1 \end{matrix}$ 个加权样点(Sigma点)来近似 $\begin{matrix} x \end{matrix}$ 的分布,将这些加权样点代入非线性函数中,得到相应的非线性函数点集,通过该点集求取变换后的均值和协方差。UKF算法的计算效率很大程度上取决于无味变换中Sigma点的个数、位置以及加权方式。标准的无味变换采用 $\begin{matrix} 2 n_{x} + 1 \end{matrix}$ 个Sigma点对称采样,缺乏一定的灵活性,同时为了减少计算量,本文通过高斯分布选取 $\begin{matrix} n_{x} + 1 \end{matrix}$ 个Sigma点,采用前一时刻状态的均值和方差作为高斯分布的均值和方差,提出了基于高斯Sigma点选取的UKF算法。其步骤如下:

(1)初始化

$\begin{matrix} \begin{matrix} x_{0 |0} = E (x_{0}) (5) \\ P_{0 |0} = E [(x_{0 |0} - E (x_{0})) {(x_{0 |0} - E (x_{0}))}^{Τ}] (6) \end{matrix} \end{matrix}$

计算Sigma点:

$\begin{matrix} \begin{matrix} χ_{0} = x_{k - 1 |k - 1}, χ_{j} ~ N (x_{k - 1 |k - 1}, P_{k - 1 |k - 1}) \\ j = 1, \dots, n_{x} (7) \\ 权值为 : \\ W_{j}^{(m)} = \{\begin{matrix} \frac{λ}{n_{x} + λ}, j = 0 \\ \frac{1}{n_{x} + λ}, j = 1,2, \dots, n_{x} \end{matrix} \\ W_{j}^{(c)} = \{\begin{matrix} \frac{λ}{n_{x} + λ} + (1 - α^{2} + β), j = 0 \\ \frac{1}{n_{x} + λ}, j = 1,2, \dots, n_{x} \end{matrix} \end{matrix} \end{matrix}$

式中: $\begin{matrix} W_{j}^{(m)} \end{matrix}$ 为求一阶统计特性时的权系数; $\begin{matrix} W_{j}^{(c)} \end{matrix}$ 为求二阶统计特性时的权系数。

(2)时间更新

$\begin{matrix} \begin{matrix} x_{j, k |k - 1} = f (χ_{j}) (8) \\ {\bar{x}}_{k |k - 1} = \overset{n_{x}}{\sum_{j = 0}} W_{j}^{(m)} x_{j, k |k - 1} (9) \\ P_{k |k - 1} = \overset{n_{x}}{\sum_{j = 0}} W_{j}^{(c)} [x_{j, k |k - 1} - {\bar{x}}_{k |k - 1}] \cdot \\ {[x_{j, k |k - 1} - {\bar{x}}_{k |k - 1}]}^{Τ} + Q_{k - 1} (10) \end{matrix} \end{matrix}$

(3)观测更新

$\begin{matrix} \begin{matrix} z_{j, k |k - 1} = h (x_{j, k |k - 1}) (11) \\ {\bar{z}}_{k |k - 1} = \overset{n_{x}}{\sum_{j = 0}} W_{j}^{(m)} z_{j, k |k - 1} (12) \\ P_{xz} = \\ \overset{n_{x}}{\sum_{j = 0}} W_{j}^{(c)} [x_{j, k |k - 1} - {\bar{x}}_{k |k - 1}] {[z_{j, k |k - 1} - {\bar{z}}_{k |k - 1}]}^{Τ} (13) \\ P_{zz} = \\ \overset{n_{x}}{\sum_{j = 0}} W_{i}^{(c)} [z_{j, k |k - 1} - {\bar{z}}_{k |k - 1}] {[z_{j, k |k - 1} - {\bar{z}}_{k |k - 1}]}^{Τ} (14) \\ K_{k} = P_{xz} P_{zz}^{- 1} (15) \\ x_{k |k} = {\bar{x}}_{k |k - 1} + K_{k} (z_{k} - {\bar{z}}_{k |k - 1}) (16) \\ P_{k |k} = P_{k |k - 1} + K_{k} P_{zz} K_{k}^{Τ} (17) \end{matrix} \end{matrix}$

2.2 改进的UPF算法

采用2.1节提出的基于高斯Sigma点选取的UKF算法产生建议分布函数,并利用MH方法对建议分布函数抽样产生的粒子进行优化,得出状态的估计值,提出了一种改进的UPF算法,称为UPF-MH算法。其具体实现步骤如下:

(1)初始化

在 $\begin{matrix} k = 0 \end{matrix}$ 时刻,从先验分布中产生样本 $\begin{matrix} {x_{0}^{i}, i = 1,2, \dots, N} \end{matrix}$ 。

$\begin{matrix} \begin{matrix} x_{0 |0}^{i} = E (x_{0}^{i}) (18) \\ P_{0 |0}^{i} = E [(x_{0}^{i} - {\bar{x}}_{0}^{i}) (x_{0}^{i} - {\bar{x}}_{0}^{i})^{Τ}] (19) \end{matrix} \end{matrix}$

(2)预测更新

对于给定的 $\begin{matrix} {\bar{x}}_{k - 1 |k - 1}^{i} \end{matrix}$ 和 $\begin{matrix} P_{k - 1 |k - 1}^{i}, \end{matrix}$ 根据式(8)~(12)求状态预测 $\begin{matrix} {\bar{x}}_{k |k - 1}^{i} \end{matrix}$ 和 $\begin{matrix} {\bar{z}}_{k |k - 1}^{i} \end{matrix}$ 。

预测协方差为:

$\begin{matrix} \begin{matrix} P_{k |k - 1}^{i} = \overset{n_{x}}{\sum_{j = 0}} W_{j}^{(c)} [x_{j, k |k - 1}^{i} - k {|k - 1}^{i}] \cdot \\ {[x_{j, k |k - 1}^{i} - {\bar{x}}_{k |k - 1}^{i}]}^{Τ} + Q_{k - 1} (20) \end{matrix} \end{matrix}$

(3)发散判断

由 $\begin{matrix} {\bar{z}}_{k |k - 1}^{iΤ} {\bar{z}}_{k |k - 1}^{i} \leq S \cdot tr [E ({\bar{z}}_{k | k - 1}^{i} {\bar{z}}_{k | k - 1}^{iΤ})] \end{matrix}$ 判断是否发散,如发散,按照式

$\begin{matrix} \begin{matrix} P_{k |k - 1}^{i} = λ \overset{n_{x}}{\sum_{j = 0}} W_{j}^{(c)} [x_{j, k |k - 1}^{i} - {\bar{x}}_{k |k - 1}^{i}] \cdot \\ {[x_{j, k |k - 1}^{i} - {\bar{x}}_{k |k - 1}^{i}]}^{Τ} + Q_{k - 1} (21) \end{matrix} \end{matrix}$

进行修正 $\begin{matrix} P_{k |k - 1}^{i} \end{matrix}$ ,若不发散则进入下一步。

(4)量测更新

根据式(13)~(17),求得:

$\begin{matrix} \begin{matrix} {\bar{x}}_{k}^{i} = {\bar{x}}_{k |k - 1}^{i} + K_{k} (z_{k} - {\bar{z}}_{k |k - 1}^{i}) (22) \\ P_{k}^{i} = P_{k |k - 1}^{i} + K_{k} P_{zz} K_{k}^{Τ} (23) \end{matrix} \end{matrix}$

(5)采样粒子

$\begin{matrix} {\hat{x}}_{k}^{i} ~ q ({\bar{x}}_{k}^{i} |{\bar{x}}_{0 ∶ k - 1}^{i}, z_{1 ∶ k}) = N ({\bar{x}}_{k}^{i}, P_{k}^{i}) (24) \end{matrix}$

计算权重:

$\begin{matrix} w_{k}^{i} \propto \frac{p (z_{k} |{\hat{x}}_{k}^{i}) \cdot p ({\hat{x}}_{k}^{i} |x_{k - 1}^{i})}{q ({\hat{x}}_{k}^{i} |x_{0 ∶ k - 1}^{i}, z_{1 ∶ k})} (25) \end{matrix}$

归一化权值:

$\begin{matrix} w_{k}^{i} = \frac{w_{k}^{i}}{\overset{N_{s}}{\sum_{i = 1}} w_{k}^{i}} (26) \end{matrix}$

(6)给定一个 $\begin{matrix} u ~ U (0,1) \end{matrix}$ ,若:

$\begin{matrix} \begin{matrix} u \leq \min \{1, \frac{p (z_{k} |{\hat{x}}_{k}^{i}) p ({\hat{x}}_{k}^{i} |{\bar{x}}_{k - 1}^{i}) q ({\hat{x}}_{k}^{i} |{\bar{x}}_{0 ∶ k - 1}^{i}, z_{1 ∶ k})}{p (z_{k} |{\bar{x}}_{k}^{i}) p ({\bar{x}}_{k}^{i} |{\bar{x}}_{k - 1}^{i}) q ({\bar{x}}_{k}^{i} |{\bar{x}}_{0 ∶ k - 1}^{i}, z_{1 ∶ k})}\} (27) \\ 则有 : x_{0 ∶ k}^{i} = ({\bar{x}}_{0 ∶ k - 1}^{i}, {\hat{x}}_{k}^{i}) (28) \\ 否则 : x_{0 ∶ k}^{i} = {\bar{x}}_{0 ∶ k}^{i} (29) \end{matrix} \end{matrix}$

(7)状态更新

$\begin{matrix} x_{k} = \overset{N}{\sum_{i = 1}} x_{k}^{i} w_{k}^{i} (30) \end{matrix}$

3 实验结果与分析

为了验证本文提出的UPF-MH算法,将其与PF、EPF、UPF算法进行比较,并采用以下两个系统进行仿真。

系统1:

$\begin{matrix} \{\begin{matrix} x_{t} = 1 + \sin (0.4 πt) + 0.5 x_{t - 1} + v_{t - 1} \\ z_{t} = \{\begin{matrix} 0.2 x_{t}^{2} + n_{t}, t \leq 30 \\ 0.5 x_{t} - 2 + n_{t}, t > 30 \end{matrix} \end{matrix} (31) \end{matrix}$

其中,过程噪声 $\begin{matrix} v_{t - 1} ~ Γ (3,2), \end{matrix}$ 量测噪声 $\begin{matrix} n_{t} ~ N (0,0.000 01) \end{matrix}$ ,采用2个不同阶次观测模型对系统状态进行观测。

系统2:

$\begin{matrix} \{\begin{matrix} x_{t} = \sin (0.04 πt) + 0.5 x_{t - 1} - 5 + v_{t - 1} \\ z_{t} = 0.2 x_{t}^{2} + n_{t} \end{matrix} (32) \end{matrix}$

其中,过程噪声 $\begin{matrix} v_{t - 1} ~ Γ (3,2) \end{matrix}$ ,量测噪声 $\begin{matrix} n_{t} ~ N (0,0.000 01), \end{matrix}$ 采用1个阶次观测模型对系统状态进行观测。

实验中,粒子数目分别设置为 $\begin{matrix} N = 100 \end{matrix}$ 和 $\begin{matrix} N = 200, \end{matrix}$ 观测时间为 $\begin{matrix} T = 50, \end{matrix}$ UT参数设置为 $\begin{matrix} α = 1, β = 0, γ = 2, \end{matrix}$ 发散判断中的可调系数 $\begin{matrix} S (S \geq 1) \end{matrix}$ 取值为1,衰减系数取值为 $\begin{matrix} λ = 2 。 \end{matrix}$ 评价标准选择均方误差以及均方误差和时间的综合评价指标,其中均方误差定义为:

$\begin{matrix} RMSE = [\frac{1}{T} \overset{T}{\sum_{t = 1}} (x_{k} - x_{k}^{i})^{2}]^{\frac{1}{2}} (33) \end{matrix}$

综合评价指标(Performance evaluation)定义为:

$\begin{matrix} PE = t \times RMSE (34) \end{matrix}$

式中: $\begin{matrix} t \end{matrix}$ 为完成一次仿真的时间。

均方误差越小,仿真时间越短,PE越小,说明算法的跟踪综合性能越高。

3.1 跟踪性能对比

表1和表2分别为系统1和系统2采样粒子数 $\begin{matrix} N = 100 \end{matrix}$ 和 $\begin{matrix} N = 200 \end{matrix}$ 时的RMSE和PE对比结果。图1和图2为PF、EPF、UPF和UPF-MH四种算法的系统1和系统2中采样粒子数 $\begin{matrix} N = 100 \end{matrix}$ 和 $\begin{matrix} N = 200 \end{matrix}$ 时产生的状态估计曲线。

表1 4种算法的RMSE值和PE值对比(系统1) Table 1 Comparison of RMSE and PE of four algorithms(system1)

表2 4种算法的RMSE值和PE值对比(系统2) Table 2 Comparison of RMSE and PE of four algorithms(system2)

	Figure Option View Download New Window
	图1 4种算法的状态估计(系统1)Fig.1 State estimation of four algorithms(system1)

	Figure Option View Download New Window
	图2 4种算法的状态估计(系统2)Fig.2 State estimation of four algorithms(system2)

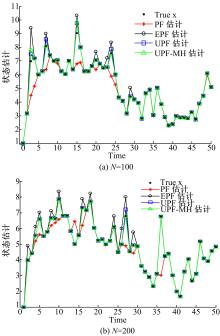
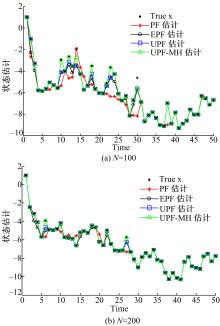
从图1可以看出,在粒子数相同的情况下,4种算法都能在一定程度上对非线性系统状态进行估计,其中UPF和UPF-MH这两种算法的估计效果好于PF和EPF的估计效果,而UPF-MH估计效果比PF、EPF和UPF有明显提高。从表1可以看出,UPF-MH的RMSE和PE值都是最小的,说明UPF-MH有较高的估计精度。从图2以及表2可以看出,在系统2中,UPF-MH的估计精度同样比其他3种算法的估计精度高。

综上,UPF-MH算法比其他3种算法具有较高的估计精度和较好的性能。

3.2 抽样粒子集中程度对比

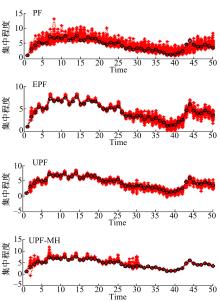
实验中将UPF-MH、PF、EPF和UPF四种算法中建议分布函数抽样产生粒子的状态值和真实状态值表示出来进行粒子集中程度的对比(粒子数设为 $\begin{matrix} N = 100 \end{matrix}$ ),如图3所示。图4是系统2中4种算法的粒子集中程度对比。其中星形符号表示抽取的粒子,圆形符号表示真实状态值。

	Figure Option View Download New Window
	图3 系统1中的粒子集中程度对比Fig.3 Comparison of particle concentration in system1

	Figure Option View Download New Window
	图4 系统2中的粒子集中程度对比Fig.4 Comparison of particle concentration in system2

从图3可以看出,在系统1中,PF算法有较多的粒子处于真实状态较远位置,也就是PF算法抽样粒子处在概率密度值非常小的区间,而EPF算法和UPF算法与PF算法相比,抽样粒子对真实后验概率分布接近程度有所改进。本文提出的UPF-MH算法相比PF、EPF、UPF算法抽样粒子更加集中在真实状态,也就是UPF-MH算法抽样粒子处在概率密度值非常大的区间。从图4可以看出,在系统2中,本文提出的UPF-MH算法相比PF、EPF、UPF算法抽样粒子更加集中在真实状态。可见,相比PF、EPF、UPF三种算法,UPF-MH算法降低了粒子退化现象。

综上,本文提出的UPF-MH算法抽样产生的粒子更能逼近真实状态的后验概率密度,提高了粒子的利用率,从而提高了估计精度。

4 结束语

提出了一种改进的UPF算法——UPF-MH,该算法通过基于高斯Sigma点选取的UKF算法产生建议分布函数,同时利用MH方法优化粒子。实验结果表明:UPF-MH算法比PF、EPF、UPF这三种算法估计精度更高,并有效降低了粒子退化现象。

本文通过构建建议分布函数来降低粒子退化现象。下一步工作将对重采样方法进行研究,通过改进重采样方法降低粒子退化现象,设计出一种有效的解决粒子退化现象的重采样算法,并与本文算法相结合应用到说话人跟踪领域。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	朱志宇. 粒子滤波算法及其应用[M]. 北京: 科学出版社, 2010. [本文引用:1]
[2]	傅惠民, 吴云章, 娄泰山. 自适应扩展增量Kalman滤波方法[J]. 航天动力学报, 2012, 27(8): 1734-1737. Fu Hui-min, Wu Yun-zhang, Lou Tai-shan. Adaptive extended incremental Kalman filter method[J]. Journal of Aerospace Power, 2012, 27(8): 1734-1737. [本文引用:1] [CJCR: 0.4202]
[3]	程水英, 余莉. 迭代无味卡尔曼滤波器的算法实现与应用评价[J]. 系统工程与电子技术, 2011, 33(11): 2546-2553. Cheng Shui-ying, Yu Li. Algorithm realization and its application evaluation of the iterated unscented Kalman filter[J]. Systems Engineering and Electronics, 2011, 33(11): 2546-2553. [本文引用:1] [CJCR: 0.499]
[4]	Gordon N J, Salmond S J, Smith A F M. Novel approach to nonlinear/non-Gaussian Bayesian state estimation[J]. Proceeding of Institute Electric Engineering, 1993, 140(2): 107-113. [本文引用:1]
[5]	Vaswani N. Particle filtering for large dimensional state spaces with multimodal observation likelihoods[J]. IEEE Trans. On Signal Processing, 2008, 56(2): 432-440. [本文引用:1]
[6]	张俊根, 姬红兵. IMM迭代扩展卡尔曼粒子滤波跟踪算法[J]. 电子与信息学报. 2010, 32(5): 1116-1120. Zhang Jun-gen, Ji Hong-bing. IMM iterated extended Kalman particle filter based target tracking[J]. Journal of Electronics & Information Technology, 2010, 32(5): 1116-1120. [本文引用:1] [CJCR: 0.087]
[7]	高社生, 薛丽, 魏文辉. 渐消自适应Unscented粒子滤波及其在组合导航中的应用[J]. 西北工业大学学报, 2012, 30(1): 27-31. Gao She-sheng, Xue Li, Wei Wen-hui. Fading adaptive UPF(unscented particle filtering) algorithm and its application to integrated navigation[J]. Journal of Northwestern Polytechnical University, 2012, 30(1): 27-31. [本文引用:1] [CJCR: 0.3229]
[8]	袁泽剑, 郑南宁, 贾新春. 高斯-厄米特粒子滤波器[J]. 电子学报, 2003, 31(7): 970-973. Yuan Ze-jian, Zheng Nan-ning, Jia Xin-chun. The Gauss-Hermite particle filter[J]. Acta Electronica Sinica, 2003, 31(7): 970-973. [本文引用:1] [CJCR: 0.686]
[9]	李翠芸, 姬红兵. 快速Metropolis- Hastings变异的遗传重采样粒子滤波器[J]. 系统工程与电子技术, 2009, 31(8): 1968-1972. Li Cui-yun, Ji Hong-bing. Genetic resampling particle filter based on fast Metropolis-Hastings mutation[J]. Systems Engineering and Electronics, 2009, 31(8): 1968-1972. [本文引用:1] [CJCR: 0.499]

2010

0.0

... 0 引言非线性、非高斯随机系统的状态估计问题在统计学、语音和图像处理、数字通信、计算机视觉、自适应估计、机器学习及自动控制等领域有着广泛应用^[1] ...

2012

0.0

0.4202

... 解决一般非线性状态估计问题常用Kalman滤波的相关改进算法,包括扩展Kalman滤波(EKF)^[2]、无味Kalman滤波(UKF)^[3]等 ...

2011

0.0

0.499

. 2011, 33(11):2546-2553 DOI:10.3969/j.issn.1001-506X.2011.11.38

Algorithm realization and its application evaluation of the iterated unscented Kalman filter

1. State Key Laboratory of Pulsed Power Laser Technology, Hefei 230037, China;2. Electronic and Engineering Institute, Hefei 230037, China

To achieve a more comprehensive and objective judgment on the application and performance of various iterated unscented Kalman filter (IUKF), three versions of IUKF are derived and the implied internal relations are identified intrinsically too. The simulation results demonstrate that a proper IUKF algorithm may be applied with 2 or 3 iterations to achieve a prominent precision profit enjoying perfect filter consistency as well when the measurement noise is not too serious and the posterior density of the nonlinear system states with unimodal can be approximated perfectly by Gaussian function, in other words, when the state variables contributing to the system nonlinearity are full instantaneous observability; otherwise the iteration profits of the IUKF relative to the UKF are hard to be guaranteed.

为了对各种迭代无味卡尔曼滤波(iterated unscented Kalman filter, IUKF)算法的应用及性能表现给出较为全面、客观的评价，分别导出并探讨了3种IUKF算法之间的内在联系。多种情况下的仿真应用表明,当观测噪声不太大,且该非线性系统状态的后验密度为可用高斯分布很好近似的单峰形式时,或者说是引起系统非线性的状态量是完全瞬时可观测时,选用恰当的IUKF算法,通过2~3次迭代,就可以在保持滤波一致性的条件下,进一步获得显著的精度收益；否则,IUKF相对于无味卡尔曼滤波(unscented Kalman filter, UKF)的迭代收益就难以保证。

... 解决一般非线性状态估计问题常用Kalman滤波的相关改进算法,包括扩展Kalman滤波(EKF)^[2]、无味Kalman滤波(UKF)^[3]等 ...

1993

0.0

... 近年来,粒子滤波^[4]被应用在解决非线性和非高斯系统状态估计问题上,但仍存在粒子退化现象 ...

2008

0.0

... 建议分布函数的选择是影响该问题一个重要因素,研究人员提出了很多基于建议分布函数选择的粒子滤波算法,其中有似然粒子滤波^[5]、扩展粒子滤波(EPF)^[6]、无味粒子滤波(UPF)^[7]和高斯-厄米粒子滤波^[8]等 ...

2010

0.0

0.087

. 2010, 32(5):1116-1120 DOI:10.3724/SP.J.1146.2009.00298

IMM iterated extended Kalman particle filter based target tracking

School of Electronic Engineering, Xidian University, Xi’an 710071, China

A new algorithm based on Interacting Multiple Model (IMM) iterated extended Kalman particle filter is proposed for maneuvering target tracking, which uses an improved Particle Filter (PF) in multiple model. First, the Iterated Extended Kalman Filter (IEKF) is modified by providing a new measurement update based on Gauss-Newton iteration, thus the linearity error is reduced. Then the modified IEKF is used to generate the importance density function of PF, which integrates the latest observation into system state transition density. Finally, simulation results are presented to demonstrate the improved performance of the proposed method over Interacting Multiple Model Particle Filter (IMMPF).

该文提出了一种交互式多模型(IMM)迭代扩展卡尔曼粒子滤波机动目标跟踪算法。该算法在多模型中使用了改进的粒子滤波器，通过对迭代扩展卡尔曼滤波(IEKF)的测量更新按照高斯牛顿方法进行修正，减小了非线性滤波带来的线性化误差，然后利用修正的IEKF来产生粒子滤波的重要性密度函数，使其融入最新观测信息。最后将所提算法与交互式多模型粒子滤波(IMMPF)进行了比较，仿真结果表明该算法具有更好的跟踪性能。

2012

0.0

0.3229

2003

0.0

0.686

. 2003, 31(7):970-973

The Gauss-Hermite particle filter

Institute of Artificial Intelligence & Robotics,Xi'an Jiaotong University,Xi'an,Shaanxi 710049,China

In this paper,a new particle filter based on sequential importance sampling (SIS) is proposed for the on-line estimation problem of non-Gauss nonlinear systems.In the new algorithm,a bank of Gauss-Hermite filter (GHF) is used for generating the importance density function.The density function integrates the new observations into system state transition density,so it can match the statea posteriori density well.As a result,while the likelihood function is situated on the tail of state transition density or observation model has higher precise,the theoretical analysis and experimental results show that the new particle filter outperforms obviously the standard particle filter and the other filters such as the extended Kalman filter (EKF),the GHF.

针对非线性、非高斯系统状态的在线估计问题,本文提出一种新的基于序贯重要性抽样的粒子滤波算法.在滤波算法中,我们用一簇高斯-厄米特滤波器(GHF)来产生重要性概率密度函数.此概率密度在系统状态的转移概率的基础上融入最新的观测数据,因此更接近于系统状态的后验概率.理论分析与实验结果表明:在观测模型具有高精度的场合或似然函数位于系统状态转移概率的尾部时,用GHF产生重要性概率密度函数的粒子滤波即高斯-厄米特粒子滤波(GHPF)的性能要明显地优于标准的粒子滤波、扩展的卡尔曼滤波、GHF.

2009

0.0

0.499

. 2009, 31(8):1968-1972

Genetic resampling particle filter based on fast Metropolis-Hastings mutation

School of Electronics Engineering, Xidian Univ., Xi'an 710071, China

A genetic resampling particle filter based on the fast mutation is proposed for removing the degeneracy phenomenon and alleviating the sample impoverishment problem in the particle filter.The algorithm chooses the fast Metropolis-Hastings(MH) moving as a mutation operator,and the traditional crossover and the traditional selection are combined with it to form a new resampling algorithm.The fast MH mutation moves the particles so that their stationary distribution is a target posterior density.The fast mutation can solve the divergence problem of the traditional mutation and produce the typical particle to reflect the features of a target density more quickly.The simulation results show that the genetic resampling based on the fast MH mutation can improve the variety of particles,remove the degeneracy phenomenon and reduce the tracking error.

为了解决传统粒子滤波器粒子退化与贫乏问题,提出了快速变异的遗传重采样粒子滤波算法.该算法将快速Metropolis-Hastings(MH)移动作为遗传算法的变异算子,使得快速变异算子与传统交叉算子、传统选择算子组合为一种新的粒子重采样算法.快速MH变异能对粒子进行移动,使得粒子的稳定分布为目标的后验概率密度分布.快速变异能有效解决一般变异算法易发散的问题,可以更快地提取到反映目标概率特征的典型粒子.实验证明,基于快速MH变异的遗传重采样方法可以快速提高粒子的多样性,避免粒子退化,减小跟踪误差.

... 该算法采用高斯Sigma点选取的自适应无味卡尔曼滤波产生建议分布函数,然后利用MH方法^[9]优化粒子,提高了对系统后验概率密度的逼近程度 ...