车载毫米波雷达对前方目标的运动状态估计

引用本文

高振海, 王竣, 佟静, 李红建, 郭章勇, 娄方明. 车载毫米波雷达对前方目标的运动状态估计. 44(6): 1537-1544
GAO Zhen-hai, WANG Jun, TONG Jing, LI Hong-jian, GUO Zhang-yong, LOU Fang-ming. Target motion state estimation for vehicle-borne millimeter-wave radar. Journal of Jilin University Engineering and Technology Edition, 44(6): 1537-1544 复制到剪切板

Permissions

车载毫米波雷达对前方目标的运动状态估计

高振海¹, 王竣¹, 佟静¹, 李红建², 郭章勇¹, 娄方明¹

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.中国第一汽车集团公司技术中心,长春 130011

通信作者:佟静(1977-),女,工程师.研究方向:汽车行驶性能测试.E-mail:tongjing@jlu.edu.cn

作者简介:高振海(197-),男,教授,博士生导师.研究方向:智能辅助驾驶.E-mail:gaozh@jlu.edu.cn

基金:“973”国家重点基础研究发展计划项目-前期研究专项(2012CB723802); 长江学者和创新团队发展计划项目(IRT1017);

摘要

基于对汽车前方目标运动特点和车载雷达信息检测机理的分析,在大地坐标系、本车的车辆运动坐标系和车载雷达运动坐标系的相对运动关系基础上,考虑了地面车辆运动以地表平面上二维运动为主、机动性小、跟踪坐标系运动的特点,建立了基于车载雷达运动坐标系的前方目标的运动状态模型。并考虑到系统过程噪声及雷达等车载传感器观测噪声的统计特性难以事先确定的问题,采用自适应卡尔曼滤波算法实现了前方目标的侧纵向速度和侧纵向位置等运动状态的完备准确实时估计。最终通过真实道路交通环境下装备毫米波雷达和高精度汽车状态测试系统的实车对比试验,对算法的可行性和估计精度进行了试验验证,试验结果显示:估计结果具有良好的精度,且长时间跟踪过程中滤波收敛稳定。

关键词: 车辆工程; 车载毫米波雷达; 前方目标运动模型; 状态估计; 自适应卡尔曼滤波

中图分类号:U461.91 文献标志码:A 文章编号:1671-5497(2014)06-1537-08

Target motion state estimation for vehicle-borne millimeter-wave radar

GAO Zhen-hai¹, WANG Jun¹, TONG Jing¹, LI Hong-jian², GUO Zhang-yong¹, LOU Fang-ming¹

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.China FAW Group Corporation R&D Center, Changchun 130011, China

Abstract

With the analysis of preceding object motion feature and vehicle-borne radar measuring principle, a novel target motion model is established in the vehicle-borne radar coordinate system. This target motion model considers the relative motion of the intertial coordinate, the vehicle coordinate and the radar coordinate system. Also other specialness of ground vehicle were taken into account in the model, such as that the motion of ground vehicle is a 2D motion because of the limitation of ground surface, the vehicle mobility is small and the tracking coordinate system is moving. The whole motion states of the preceding target, including the longitudinal and lateral velocities, the longitudinal and lateral positions were estimated by the algorithm of adaptive Kalman filter, because it was difficult to determine the statistics of the system process noise and measure noise. Finally, road experiments, in which the host car was equipped with millimeter-wave radar and the preceding car was equipped with high precision automotive testing equipments, were carried out to verify the feasibility and performance of the estimation method. The results prove that the method can provide fine estimation accuracy, better filter convergence and stability.

Keyword: vehicle engineering; vehicle-borne millimeter-wave radar; target motion model; state estimation; adaptive Kalman filter

Show Figures

0 引言

近年来,以雷达和计算机视觉等先进信息传感技术为基础的车道偏离预警、前方防碰撞预警及自适应巡航控制系统等汽车先进驾驶辅助系统(Advanced driver assistance systems,ADAS)已成为国际汽车安全技术的研究热点^{[ 1, 2, 3, 4]}。

目前戴姆勒、博世、德尔福等国际知名的整车厂家和汽车电控系统供应商多采用具有较强环境适应性的毫米波雷达检测前方中远距离范围的障碍物等目标^{[ 4, 5, 6]}。研究表明,基于车载雷达对本车前方交通环境信息的检测,获取前方障碍物的全面信息(如侧纵向位置、侧纵向速度),乃至通过对前方目标运动状态的跟踪进一步预测其未来走行轨迹和前方道路曲率,可以获得完善的前方道路交通环境信息,大幅提升前方防碰撞预警、自适应巡航控制乃至预测式紧急制动等辅助驾驶系统的控制性能品质和乘员接受性。但受限于车载毫米波雷达的测量原理及技术发展现状,现有的车载毫米波雷达仅可以直接量测前方目标与本车之间的相对距离、方位角、径向速度,进而通过坐标转换得到前方障碍目标的侧纵向位置信息。鉴于以上问题和研发需求,近年来研究人员开展了基于车载雷达的前方物体的状态信息估计研究。

汽车状态参数估计技术研究由来已久。早期研究主要为了满足制动防抱死系统(Anti-lock brake system,ABS)和汽车稳定性控制系统(Electronic stability program,ESP)等电控系统的研究需求^{[ 7, 8]},利用易于低成本测试的轮速、横摆角速度等状态变量,基于卡尔曼滤波算法和汽车动力学模型实现汽车质心侧偏角^{[ 9]}、汽车侧纵向速度^{[ 10, 11]}、路面附着系数^{[ 12, 13]}等难以直接量测或低成本测量信息的估计。研究中针对汽车动力学特性呈强非线性、量测变量噪声统计特性不确定等问题,在经典卡尔曼滤波算法基础上,引入了扩展卡尔曼滤波、粒子滤波、自适应卡尔曼滤波等状态估计算法。

伴随着辅助驾驶系统研究的开展及其对本车周围交通环境信息感知的需求,博世、德尔福等公司研究人员提出了汽车前方障碍物的状态估计算法。以期获得除相对运动状态信息以外更为完善、全面的前车运动状态信息,实现更为准确的有效目标识别,并基于获取的前方障碍物完备信息对前方道路曲率进行估计^{[ 5, 6]}。研究中大多是借鉴面向飞机、导弹等飞行物检测的军用雷达机动目标跟踪方法,利用可直接量测获取的前方物体与本车的相对位置关系及相对速度信息,建立目标机动模型和侧纵向速度状态估计算法,获取前方物体侧纵向速度和加速度信息^{[ 14, 15, 16, 17]}。

汽车运动受道路形状、路面附着及汽车自身驱动、制动及转向能力的限制,相对飞机、导弹等飞行器而言无法实现大加速度机动行驶,且基本处于平面二维运动,但现有研究对车辆行驶与飞行物运动规律之间的差异性考虑不多;同时,军用雷达多为地基雷达,相对大地坐标系处于静止状态,而车载雷达相对大地坐标系始终保持相对运动状态。

针对以上车载毫米波雷达目标跟踪和车辆运动状态具有机动性小、跟踪坐标系运动的特殊性,本文结合对汽车运动规律的分析和车载雷达的信息检测机理,首先介绍了适用于描述小机动性目标的常加速度模型(Constant acceleration,CA)。在此基础上,基于大地坐标系、本车的车辆运动坐标系和车载雷达运动坐标系的相对关系,建立了基于车载雷达运动坐标系的前方目标的运动状态模型和完整运动状态观测模型;最终采用自适应卡尔曼滤波算法,实现了前方目标的侧纵向速度和侧纵向位置等运动状态的完备准确实时估计,并通过真实道路交通环境下装备毫米波雷达和高精度汽车状态测试系统的实车试验,验证了算法的可行性。

1 基于车载雷达运动坐标系的前方目标运动模型

本文研究涉及到的大地坐标系、车辆运动坐标系和车载雷达运动坐标系如图1所示。本车车体运动及实际目标的运动状态描述是基于大地坐标系 x₀ y₀ z₀的。

	Figure Option View Download New Window
	图1 坐标系示意图Fig.1 Coordinate systems

本车的车辆运动坐标系 x_v y_v z_v是与车体固联的坐标系,令其原点在车辆质心COG上; x_v轴与车辆纵轴线平行,方向指向车辆前方; y_v轴与车辆侧向轴线平行,方向指向车辆左侧; z_v轴与车辆铅垂轴线平行,方向指向车辆上方。车身绕 x_v轴的转动称为侧倾运动( φ);绕 y_v轴的转动称为俯仰运动( θ);绕 z_v轴的转动称为横摆运动( ψ)。

车载雷达安装在车辆前部,并与车体固联,且保证雷达波束对准汽车纵轴。为此,车载雷达运动坐标系 x_s y_s与车体坐标系 x_v y_v平行, x_s轴方向与车辆纵轴 x_v方向相同; y_s轴方向与车辆 y_v轴方向相反(即指向车辆右侧)。坐标系原点 O_s在本车的车辆运动坐标系中的坐标为( x_o_s, y_o_s, z_o_s)。

1.1 描述目标运动的常加速度模型

在建立目标运动模型时,一般不考虑目标的形状而将其视为空间中一个点,并基于牛顿运动定律对目标运动规律进行描述^{[ 18]},其模型如下:

$\begin{matrix} \{\begin{matrix} x_{k + 1} = f_{k} (x_{k}, u_{k}, w_{k}) \\ z_{k} = h_{k} (x_{k}) + v_{k} \end{matrix} (1) \end{matrix}$

式中: x_k、 z_k、 u_k分别为 k时刻目标的状态、观测和控制输入向量; w_k、 v_k分别为过程噪声和量测噪声; f_k、 h_k分别为关于目标状态、控制输入的时变函数。其中,目标在空间内的运动状态变化将通过位移 x、速度 $\begin{matrix} \overset{\cdot}{x} \end{matrix}$ 、加速度 $\begin{matrix} \overset{\cdot \cdot}{x} \end{matrix}$ 参数描述。

与飞机等飞行物相比,路面行驶车辆的车速变化较为缓慢,常规行驶时侧纵向加速度变化较小,为此本文采用表征机动性不大的目标运动过程的CA模型来描述前方目标的运动^{[ 18]}。

令状态变量为 x=[ x, $\begin{matrix} \overset{\cdot}{x} \end{matrix}$ , $\begin{matrix} \overset{\cdot \cdot}{x} \end{matrix}$ ]^T,目标状态空间如下式所示:

$\begin{matrix} \overset{\cdot}{x} (t) = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{matrix}] x (t) + [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}] w (t) (2) \end{matrix}$

对式(2)进行离散化,可以得到CA模型的离散模型:

$\begin{matrix} x (k + 1) = Φ (k + 1, k) x (k) + G (k + 1, k) w (t) (3) \end{matrix}$

式中: Φ( k+1, k)为系统状态转移矩阵,其表达式为: Φ( k+1, k) = $\begin{matrix} [\begin{matrix} 1 & T & 0.5 T^{2} \\ 0 & 1 & T \\ 0 & 0 & 1 \end{matrix}] \end{matrix}$ ; G( k+1, k)为系统噪声系数矩阵,其表达式为: G( k+1, k) = $\begin{matrix} {[\begin{matrix} T^{3} / 6 & T^{2} / 2 & T \end{matrix}]}^{T} \end{matrix}$ ; w( t) ~N(0, σ²)是一个随机白噪声过程; T为采样时间间隔。

1.2 前方目标的运动状态模型

如前所述,车载雷达检测的前方目标运动规律与军用雷达检测的飞机、导弹等飞行器运动规律存在一定的差异性:

(1)车载雷达检测的前方目标主要是车辆、行人、路侧隔离带、树木、广告牌等。这些目标一般无垂直方向的运动或垂直方向运动速度极小。因此,本文研究中可忽略目标在垂直方向的运动,只需要关注物体在雷达波束平面内的运动。目标状态估计问题可以简化为在大地坐标系下水平面内物体的运动状态估计。

(2)自适应巡航控制系统等先进辅助驾驶系统一般工作在高速公路上,高速公路大部分路段都是直道,且弯道路段曲率较小,车辆横摆角速度通常非常小。因此,本文研究中可忽略横摆角速度影响。此时车载雷达运动坐标系与车辆运动坐标系平行,且固联在一起,具有相同运动状态(不考虑雷达传感器安装支架自身振动变形)。

(3)车载雷达检测的目标信息都是基于车载雷达运动坐标系,并非基于大地坐标系的位置信息。针对目标相对大地坐标系的状态信息无法直接测量的问题,前期研究中大多是利用车辆运动状态和雷达测量信息实现前方雷达目标相对大地坐标系的状态信息的估计。但由于车辆行驶轨迹及航向角是通过数值积分获得,积分过程中的误差将会随时间累计,而使结果的可信度随着估计时间的增长迅速降低,为此单纯依靠现有低成本车载传感器(轮速传感器、侧向加速度传感器、横摆角速度传感器)无法获得可信的本车车辆运动轨迹信息。

针对以上分析得出的前方目标运动规律和车载雷达检测的特点,本文基于车辆运动坐标系建立前方目标运动模型,并基于车载雷达运动坐标系进行目标运动状态估计。

利用基于大地坐标系的常加速度模型,前方目标在大地坐标系下的运动方程为:

$\begin{matrix} \{\begin{matrix} \overset{\cdot \cdot}{x} (t) = a \\ \overset{\cdot}{x} (t) = \overset{\cdot}{x} (0) + at \\ x (t) = x (0) + \overset{\cdot}{x} (0) t + \frac{1}{2} a t^{2} \end{matrix} (4) \end{matrix}$

式中: $\begin{matrix} \overset{\cdot \cdot}{x} \end{matrix}$ ( t)为目标的加速度; $\begin{matrix} \overset{\cdot}{x} \end{matrix}$ ( t)为目标的速度; x( t)为目标的位置; a为目标的加速度值; $\begin{matrix} \overset{\cdot}{x} \end{matrix}$ (0)为目标的初速度; x(0)为目标的初始位置。

车载雷达运动坐标系相对大地坐标系的运动方程为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot \cdot}{x}}_{R} (t) = a_{v} \\ {\overset{\cdot}{x}}_{R} (t) = {\overset{\cdot}{x}}_{v} (0) + a_{v} t \\ x_{R} (t) = x_{R} (0) + {\overset{\cdot}{x}}_{v} (0) t + \frac{1}{2} a_{v} t^{2} \end{matrix} (5) \end{matrix}$

式中: $\begin{matrix} {\overset{\cdot \cdot}{x}}_{R} \end{matrix}$ ( t)为雷达的加速度; $\begin{matrix} {\overset{\cdot}{x}}_{R} \end{matrix}$ ( t)为雷达的速度; x_R( t)为雷达的位置; a_v为车辆的加速度; $\begin{matrix} {\overset{\cdot}{x}}_{v} \end{matrix}$ (0)为车辆的初速度; x_R(0)为雷达的初始位置。

由式(4)(5)可以推导出目标在车载雷达运动坐标系中的运动方程如下:

$\begin{matrix} \{\begin{matrix} x_{ob j_R} (t) = x (t) - x_{R} (t) = [x (0) - x_{R} (0)] + \\ [\overset{\cdot}{x} (0) - {\overset{\cdot}{x}}_{v} (0)] t + \frac{1}{2} [a - a_{v}] t^{2} \\ {\overset{\cdot}{x}}_{obj_R} (t) = [\overset{\cdot}{x} (0) - {\overset{\cdot}{x}}_{v} (0)] + [a - a_{v}] t \\ {\overset{\cdot \cdot}{x}}_{obj_R} (t) = [a - a_{v}] \end{matrix} (6) \end{matrix}$

式中: x_{obj_R}( t)为目标的位置,即目标相对雷达的距离; $\begin{matrix} {\overset{\cdot}{x}}_{o bj_R} \end{matrix}$ ( t)为目标的速度; $\begin{matrix} {\overset{\cdot \cdot}{x}}_{obj_R} \end{matrix}$ ( t)为目标的加速度。

由式(6)可知,目标在车载雷达运动坐标系中的纵向运动可采用常加速度模型来表示。目标物体侧向运动推导过程与式(4)(5)(6)相似,即目标侧向运动也可采用常加速度模型来描述。当本车横摆角速度较小时,在大地坐标系下可以用常加速度模型表示本车运动过程,在车辆运动坐标系(车载雷达运动坐标系)下目标物体的运动过程也可以用常加速度模型表示,其加速度为目标物体的加速度与本车加速度之差。

1.3 前方目标状态估计的状态模型和量测模型

鉴于车载雷达前方目标运动状态估计主要关注目标的位置及侧纵向速度信息,本文采用向量 x=[ x, $\begin{matrix} \overset{\cdot}{x} \end{matrix}$ , $\begin{matrix} \overset{\cdot \cdot}{x} \end{matrix}$ , y, $\begin{matrix} \overset{\cdot}{y} \end{matrix}$ , $\begin{matrix} \overset{\cdot \cdot}{y} \end{matrix}$ ]^T来描述前方物体的运动状态。其中( x, y)表示物体在 xy平面内的位移;( $\begin{matrix} \overset{\cdot}{x} \end{matrix}$ , $\begin{matrix} \overset{\cdot}{y} \end{matrix}$ )表示物体在 xy平面内的速度;( $\begin{matrix} \overset{\cdot \cdot}{x} \end{matrix}$ , $\begin{matrix} \overset{\cdot \cdot}{y} \end{matrix}$ )表示物体在 xy平面内的加速度。

前方目标的侧纵向运动方程可以表示为:

$\begin{matrix} \begin{matrix} \overset{\cdot}{x} (t) = diag [Λ, Λ] x (t) + diag [B, B] w (t) (7) \\ Λ = [\begin{matrix} 0 & 1 & 0 \\ 0 & 0 & 1 \\ 0 & 0 & 0 \end{matrix}], B = [\begin{matrix} 0 \\ 0 \\ 1 \end{matrix}] \end{matrix} \end{matrix}$

式中:状态向量 x= $\begin{matrix} {[x, \overset{\cdot}{x}, \overset{\cdot \cdot}{x}, y, \overset{\cdot}{y}, \overset{\cdot \cdot}{y}]}^{T} \end{matrix}$ ; Λ为单一坐标轴上的目标运动状态的系统矩阵; B为过程噪声矩阵; w( t) =[ w_x( t), w_y( t)]^T, w_x( t) ~N(0, $\begin{matrix} {σ_{wx}}^{2} \end{matrix}$ )、 w_y( t) ~N(0, $\begin{matrix} {σ_{wy}}^{2} \end{matrix}$ )是相互独立的随机白噪声过程。

与式(7)对应的离散时间模型表示为:

$\begin{matrix} x_{k + 1} = diag [Φ, Φ] x_{k} + diag [G, G] w_{k} (8) \end{matrix}$

前方目标运动状态的观测方程为:

$\begin{matrix} \begin{matrix} z (t) = Cx (t) + v (t) (9) \\ C = [\begin{matrix} 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 & 0 & 0 \end{matrix}] \end{matrix} \end{matrix}$

式中: z( t)为观测向量; C为输出状态矩阵; v( t) =[ v_x( t), $\begin{matrix} v_{\overset{\cdot}{x}} \end{matrix}$ ( t), v_y( t)]^T, v( t) ~N(0, R)是高斯白噪声过程。

观测方程(9)离散后表示为:

$\begin{matrix} z_{k} = C x_{k} + v_{k} (10) \end{matrix}$

式中: z_k为观测向量; v_k为高斯白噪声序列。

2 基于自适应卡尔曼滤波器的前方目标运动状态估计

针对本文建立的前方目标运动模型,并考虑到雷达等各种车载传感器观测噪声的统计特性难以事先确定,本文在文献[8]的基础上,采用Sage自适应Kalman滤波算法,利用估计残差序列估计修正观测噪声和系统噪声协方差阵,进而实现对目标运动状态的实时准确估计。

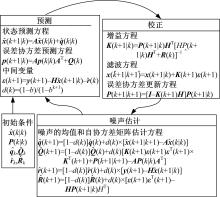
Sage自适应滤波算法分为预测过程、校正过程和噪声估计过程3部分,如图2所示。预测过程根据当前时刻的系统状态获得下一时刻的先验估计;校正过程将观测和先验估计相结合获得改进的系统后验估计;噪声估计过程则利用前 m步残差序列估计和修正观测噪声协方差阵和系统噪声协方差阵。

	Figure Option View Download New Window
	图2 自适应卡尔曼滤波算法及其滤波方程示意图Fig.2 Adaptive Kalman filter algorithm and key equations

图2中, x( k)和 y( k)为 k时刻的状态向量和量测向量; A为系统状态转移矩阵; H为输出状态矩阵; K_k为卡尔曼增益矩阵; P为预测协方差矩阵; q_k、 Q_k分别为系统噪声的均值和自协方差矩阵; r_k、 R_k分别为观测噪声的均值和自协方差矩阵。 b为遗忘因子(0 <b<1)。采用遗忘因子可以限制滤波器的记忆长度,加大信息数据对估计的作用。

本文根据式(7)(8)(9)(10)设计了基于自适应卡尔曼滤波器的目标跟踪滤波算法,其中式(8)为卡尔曼滤波器的状态方程,式(10)为滤波器的量测方程。

滤波器输入为雷达传感器输出的目标信息,包括目标的相对距离、方位角、相对速度:

$\begin{matrix} z_{k} = [x, v_{r} {, y]}^{T} (11) \end{matrix}$

式中:( x, y)为目标在车载雷达运动坐标系中的位置; v_r为目标的径向速度。

本文在应用卡尔曼滤波器实现对目标运动状态估计的过程中,重点关注如下问题:

(1)车载雷达信息输出的前方目标极坐标系与直角坐标系的转换

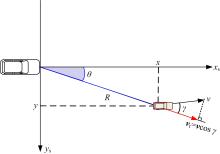
如图3所示,雷达传感器基于雷达传感器坐标输出目标的回波信息,并以极坐标的形式输出目标点的距离 R、方位角 θ、相对速度 v_r信息。其中,距离 R为雷达与目标之间的距离;方位角 θ代表目标回波与雷达主波中心线(瞄准轴) x_s的夹角;相对速度 v_r为目标的径向速度或距离 R随时间的变化率。若目标的速度矢量 v与雷达和目标间的视线夹角为 γ,则 v_r =v·cos γ, v为目标的速度矢量或者速度矢量的幅值^{[ 19]}。

	Figure Option View Download New Window
	图3 雷达传感器坐标及其量测信息Fig.3 Coordinate system and measurement of radar

为此,本文首先将雷达基于极坐标系的目标量测信息转换至直角坐标系(车载雷达运动坐标系)中,转换公式为:

$\begin{matrix} \{\begin{matrix} x = R \cdot cosθ \\ y = R \cdot sinθ \end{matrix} (12) \end{matrix}$

式中:( x, y)为目标位置在直角坐标系中的表示。

目标跟踪滤波器输出 $\begin{matrix} \hat{x} \end{matrix}$ 为目标相对车辆坐标系的侧纵向距离、速度和加速度,即滤波器输出为:

$\begin{matrix} \hat{x} = [\hat{x}, \hat{y}, {\hat{v}}_{x}, {\hat{v}}_{y}, {\hat{a}}_{x}, {\hat{a}}_{y}]^{T} (13) \end{matrix}$

式中: $\begin{matrix} \hat{x} \end{matrix}$ , $\begin{matrix} \hat{y} \end{matrix}$ 为目标相对车辆的纵侧向距离; $\begin{matrix} {\hat{v}}_{x} \end{matrix}$ , $\begin{matrix} {\hat{v}}_{y} \end{matrix}$ 为目标相对车辆坐标系的纵侧向速度; $\begin{matrix} {\hat{a}}_{x} \end{matrix}$ , $\begin{matrix} {\hat{a}}_{y} \end{matrix}$ 为目标相对车辆坐标系的纵侧向加速度。

(2)前方目标的运动学补偿

对于目标物体的位置信息,一方面由于辅助驾驶系统主要关注前方障碍物与本车的相对侧纵向距离信息;另一方面本车在大地坐标系下的准确位置信息需要高精度的GPS才能获取,因此运动补偿主要针对物体的速度和加速度。由式(6)可知,基于车辆运动坐标系的目标状态估计方法输出的目标运动参数为目标在大地坐标系的运动参数与车辆在大地坐标系中的运动参数之差,而实际应用中需要的是目标相对大地坐标系的运动参数,故还需要对估计后的目标运动参数(速度和加速度)进行补偿。

目标在大地坐标系下的速度和加速度用 v_obj和 a_obj表示,则:

$\begin{matrix} \{\begin{matrix} v_{obj} = \hat{v} + v_{v} \\ a_{obj} = \hat{a} + a_{v} \end{matrix} (14) \end{matrix}$

式中: v_obj, a_obj分别为目标实际的速度和加速度; $\begin{matrix} \hat{v} \end{matrix}$ =[ $\begin{matrix} {\hat{v}}_{x} \end{matrix}$ , $\begin{matrix} {\hat{v}}_{y} \end{matrix}$ ]^T为滤波器输出的速度估计值; $\begin{matrix} \hat{a} \end{matrix}$ =[ $\begin{matrix} {\hat{a}}_{x} \end{matrix}$ , $\begin{matrix} {\hat{a}}_{y} \end{matrix}$ ]^T为滤波器输出的加速度估计值; v_v, a_v分别为车辆的侧纵向速度和侧纵向加速度。

3 实车试验验证及结果分析

试验工况为前方车辆以25 km/h速度行驶,在12 s后制动减速。

试验中本车为装备了毫米波雷达的辅助驾驶试验车;前车则装备了高精度的CORRSYS DATRON公司SC-E双轴非接触式光电测速仪和Crossbow公司VG700光纤陀螺仪,分别用于测量实际侧纵向速度信息和侧纵向加速度信息,并与本文算法求解的状态估计信息做精度对比。本文中采用的毫米波雷达及测试仪器的测量范围和精度如表1所示。

表1 仪器测量范围及精度 Table 1 Measure range and accuracy of the sensor and measurement instruments

试验中毫米波雷达安装在试验车前保险杠位置;非接触式光电测速仪安装在前车后部;陀螺仪安装在前车车内质心位置附近,如图4所示。最终,试验数据后处理时,光电测速仪和陀螺仪的输出结果都修正到质心处的侧纵向速度及加速度。

	Figure Option View Download New Window
	图4 仪器安装位置示意图Fig.4 Sensor and instruments mounted on the car

图5中的3个图片为目标跟踪过程中 t=0 s, t=10 s, t=20 s时刻的道路环境场景。图中矩形框中的车辆即为被跟踪的目标物体。

雷达从0~20 s内检测到的目标如图6所示。矩形框表示前方车辆的测量值;实线表示估计结果。起始时刻, 图5(a)框中的车辆在图6中标识为方框;结束时刻, 图5(c)框中的车辆对应图6中圆圈。

	Figure Option View Download New Window
	图5 目标跟踪场景Fig.5 Scenario of a road experiment

	Figure Option View Download New Window
	图6 目标物体运动轨迹及跟踪效果Fig.6 Object trajectory measured by radar and object tracking result

图7为目标物体相对本车的纵向距离及侧向距离随时间的变化过程。试验结果显示,滤波器估计结果能很好地跟踪雷达测量值。

图8为目标物体的纵向、侧向速度的测量值和估计值对比曲线。纵向速度估计值与实际测量值最大偏差为0.433 km/h;侧向速度估计值与实际测量值最大偏差为0.317 km/h,即速度估计值绝对偏差在0.5 km/h以内。

	Figure Option View Download New Window
	图7 目标物体相对本车纵向和侧向距离测量值与估计值对比Fig.7 Measured and estimated value of object longitudinal & lateral position

	Figure Option View Download New Window
	图8 目标物体纵向和侧向速度实际值与估计值对比Fig.8 Measured and estimated value of object longitudinal & lateral velocity

	Figure Option View Download New Window
	图9 目标物体纵向和侧向加速度实际值与估计值对比Fig.9 Measured and estimated value of object longitudinal & lateral acceleration

本文提出的常加速度模型不仅适用于匀加速运动的前方物体,对非匀加速运动也具有一定的跟踪滤波功能。图9为前方目标物体进行非匀加速运动时侧纵向加速度实际测量值和估计值对比曲线。试验中,前车最大纵向加速度为0.26 m/s²,最小纵向加速度为-1.02 m/s²(制动),最大侧向加速度为1.05 m/s²,最小侧向加速度为-1.07 m/s²。由图9可见,目标物体加速度估计值与实际测试值表现出良好的一致性,纵向加速度估计值与实际测量值最大偏差为0.211 m/s²;侧向加速度估计值与实际测量值最大偏差为0.284 m/s²。

表2为估计值相对于实际值的误差分析结果。侧纵向速度、加速度的平均绝对误差、均方根误差以及平均相对误差体现了估计方法具有较好的估计精度,平均相对误差均小于8.5%。

表2 前方目标运动状态估计误差分析 Table 2 Error analysis of the target motion state estimation

4 结束语

探讨了车载毫米波雷达应用过程中面临的目标跟踪问题,根据汽车前方目标运动规律与车载雷达量测均为相对量等特点,在常加速度模型的基础上,基于大地坐标系、本车的车辆运动坐标系和车载雷达运动坐标系的相对关系,推导建立了基于车载雷达运动坐标系的前方目标的运动状态模型和完整运动状态观测模型。在此基础上,建立了基于车载雷达坐标系和自适应卡尔曼滤波器的目标运动状态估计算法,为车载雷达前方目标跟踪及状态估计提供了一种有效的解决方法。实车对比试验结果表明:基于本文提出方法得出的前方目标速度和加速度等实时状态估计信息与车载高精度运动状态测试系统的检测结果具有良好的一致性,估计精度较高,且长时间跟踪过程中滤波收敛稳定,未出现跟踪发散现象。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王建强, 王海鹏, 张磊, 等. 基于电控液压制动装置的车辆主动报警/避撞系统[J]. 吉林大学学报: 工学版, 2012, 42(4): 816-822. Wang Jian-qiang, Wang Hai-peng, Zhang Lei, et al. Vehicle collision warning and avoidance system based on electronic hydraulic brake device[J]. Journal of Jilin University (Engineering and Technology Edition), 2012, 42(4): 816-822. [本文引用:1] [CJCR: 0.701]
[2]	金立生, Van Arem Bart, 杨双宾, 等. 高速公路汽车辅助驾驶安全换道模型[J]. 吉林大学学报: 工学版, 2009, 39(3): 582-586. Jin Li-sheng, Van Arem Bart, Yang Shuang-bin, et al. Safety lane change model of vehicle assistant driving on highway[J]. Journal of Jilin University(Engineering and Technology Edition), 2009, 39(3): 582-586. [本文引用:1] [CJCR: 0.701]
[3]	李向瑜, 高振海, 袁昌碧, 等. 汽车巡航控制系统的环境评估[J]. 吉林大学学报: 工学版, 2008, 38(增刊1): 28-31. Li Xiang-yu, Gao Zhen-hai, Yuan Chang-bi, et al. Environment evaluation of vehicle cruise control[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(Sup. 1): 28-31. [本文引用:1] [CJCR: 0.701]
[4]	Sarholz F, Mehnert J, Klappstein J, et al. Evaluation of different approaches for road course estimation using imaging radar[C]∥International Conference on Intelligent Robots and Systems, San Francisco CA, USA, 2011: 4587-4592. [本文引用:1]
[5]	Uhler W, Scherl M, Lichtenberg B. Driving course prediction using distance sensor data[C]∥SAE Paper, 1999-01-1234. [本文引用:1]
[6]	Schiffmann J K, Widmann G R. Model-based scene tracking using radar sensors for intelligent automotive vehicle systems[C]∥IEEE Conference on Intelligent Transportation Systems, Boston MA, USA, 1997: 421-426. [本文引用:1]
[7]	赵又群. 汽车动力学中若干关键状态和参数估计研究的现状与发展[J]. 中国机械工程, 2010, 21(10): 1250-1253. Zhao You-qun. Present state and perspectives of estimation research for several key states and parameters in vehicle dynamics[J]. China Mechanic Engineering, 2010, 21(10): 1250-1253. [本文引用:1] [CJCR: 0.751]
[8]	高越, 高振海, 李向瑜. 基于自适应Kalman滤波的汽车横摆角速度软测量算法[J]. 江苏大学学报: 自然科学版, 2005, 26(1): 24-27. Gao Yue, Gao Zhen-hai, Li Xiang-yu. Soft measurement method for vehicle yaw rate based on adaptive Kalman filter[J]. Journal of Jiangsu University (National Science Edition), 2005, 26(1): 24-27. [本文引用:1]
[9]	Hac A, Simpson M D. Estimation of vehicle side slip angle and yaw rate[C]∥SAE Paper, 2000-01-0696. [本文引用:1]
[10]	Jiang Fang-jun, Gao Zhi-qiang. An adaptive nonlinear filter approach to the vehicle velocity estimation for ABS[C]∥IEEE Conference on Control Applications, Anchorage, USA, 2000: 490-495. [本文引用:1]
[11]	Farrelly J, Wellstead P. Estimation of vehicle lateral velocity[J]. IEEE Conference on Control Applications, Dearborn MI, USA, 1996: 552-557. [本文引用:1]
[12]	Liu C, Peng H. Road friction coefficient estimation for vehicle path prediction[J]. Vehicle System Dynamics, 1996, 25(Sup. 1): 413-425. [本文引用:1] [JCR: 0.766]
[13]	Ito M, Yoshioka K, Saji T. Estimation of road surface conditions using wheel speed behavior[J]. JSAE Review, 1995, 16(2): 221-222. [本文引用:1] [JCR: 0.145]
[14]	陈利斌, 佟明安. 机动目标跟踪的交互式多模型自适应滤波算法[J]. 火力与指挥控制, 2000, 25(4): 36-38. Chen Li-bin, Tong Ming-an. Interacting multiple model adaptive filtering algorithm for maneuvering tracking[J]. Fire Control & Command Control, 2000, 25(4): 36-38. [本文引用:1]
[15]	左东广, 韩崇昭, 卞树檀, 等. 闪烁噪声机动目标跟踪的模型集交互跟踪算法[J]. 系统仿真学报, 2004, 16(4): 767-771. Zuo Dong-guang, Han Chong-zhao, Bian Shu-tan, et al. Model sets interacting algorithm for maneuvering target tracking in the presence of glint noise[J]. Journal of System Simulation, 2004, 16(4): 767-771. [本文引用:1] [CJCR: 0.914]
[16]	Blackman S S. Multiple hypothesis tracking for multiple target tracking[J]. Aerospace and Electronic Systems Magazine, 2004, 19(1): 5-18. [本文引用:1] [JCR: 0.343]
[17]	Pitre R R, Jilkov V P, Li X R. A comparative study of multiple-model algorithms for maneuvering target tracking[C]∥Proceedings of SPIE-The International Society for Optical Engineering, Orland o FL, USA, 2005: 549-560. [本文引用:1]
[18]	石章松, 刘忠等. 目标跟踪与数据融合理论及方法[M]. 北京: 国防工业出版社, 2010. [本文引用:2]
[19]	张明友, 汪学刚. 雷达系统[M]. 3版. 北京: 电子工业出版社, 2011. [本文引用:1]

2012

0.0

0.701

. 2012, 42(4):816-822

Vehicle collision warning and avoidance system based on electronic hydraulic brake device

1. State Key Laboratory of Automotive Safety and Energy, Tsinghua University, Beijing 100084, China;<br>2. Beijing Institute of Space Launch Technology, Beijing 100076, China

A forward vehicle collision warning and avoidance system was proposed based on the electronic hydraulic brake device to prevent the rear-end collision. The system real-timely judges the dangerous level of rear-end collision with a time-to-collision algorithm based on the running situations of the front vehicle and this vehicle. When the collision possibility is detected, the system warns the driver with vision and hearing warnings and achieves the vehicle active collision avoidance by the electronic hydraulic brake. An experiment platform was established on a real vehicle to verify the brake pressure control effect. Introducing the system in a test vehicle, the test results show that the system provided timely the stepped collision warning and the brake assistance, enhancing the vehicle driving safety.

为预防道路尾随相撞事故,开发了一种基于电控液压制动装置的车辆前向报警/避撞系统。该系统根据前方车辆和自车的运动状态,基于碰撞时间实时判断尾随相撞危险度。在危险情况下,系统通过视听觉报警为驾驶员提供警示,并以电控液压制动的方式实现车辆的主动避撞。利用电控液压制动装置搭建了实验平台,对制动压力控制效果进行了验证。将系统安装于试验样车,实车试验结果表明,该系统能为驾驶员提供分级碰撞报警警示和制动辅助,以提高行车安全性。

2009

0.0

0.701

. 2009, 39(3):582-586

Safety lane change model of vehicle assistant driving on highway

1.College of Transportation, Jilin University, Changchun 130022, China；2.Centre for Transport Studies, Twente University, Enschede, 7522LD,Netherlands

To deal with the problem of traffic accidents such as vehicle collision during the conscious lane change of the vehicle on the highway under dangerous conditions, a now safety lane change model was established on the basis of the previously studied and developed lane departure warning system. The model considered the typical lane change scenario and more actual behavior that most driver often accelerate their vehicles during the lane change process. A simulation program was developed to analyze the model performance based on the software Matlab 7.0. The established model was compared with the developed by California University and the result showed this model is more practical. It can be used to establish the vehicle assistant driving system for lane change.

为解决高速公路行车危险状态下驾驶员有意识换道过程中发生的车辆碰撞等交通事故问题，在前期研究车道偏离预警的基础上.针对确立的典型换道场景，建立了更加符合实际的基于换道过程中车辆加速行为的安全换道模型，并借助Matlab软件开发的仿真程序对建立的模型进行了仿真分析。结果表明，本文建立的模型具有较好的实用性，可为进一步建立车辆安全换道辅助系统奠定基础。

2008

0.0

0.701

2011

0.0

1999-01-1234

0.0

1997

0.0

2010

0.0

0.751

2005

0.0

. 2005, 26(1):24-27

Soft measurement method for vehicle yaw rate based on adaptive Kalman filter

利用参数软测量技术,提出了基于自适应Kalman滤波和汽车两自由度动力学模型的横摆角速度软测量算法.该算法实现了横摆角速度的线性最小均方误差估计,且可对汽车行驶过程中的系统噪声和观测噪声统计特性进行在线估计.仿真与场地试验结果对比验证了该算法的有效性,同时软测量技术的采用也为汽车状态参数测量提供了一条可行的、准确且低成本的研究思路.

2000

0.0

... 早期研究主要为了满足制动防抱死系统(Anti-lock brake system,ABS)和汽车稳定性控制系统(Electronic stability program,ESP)等电控系统的研究需求^[7,8],利用易于低成本测试的轮速、横摆角速度等状态变量,基于卡尔曼滤波算法和汽车动力学模型实现汽车质心侧偏角^[9]、汽车侧纵向速度^[10,11]、路面附着系数^[12,13]等难以直接量测或低成本测量信息的估计 ...

2000

0.0

1996

0.0

1996

0.766

0.0

1995

0.145

0.0

2000

0.0

. 2000, 25(4):36-38

Interacting multiple model adaptive filtering algorithm for maneuvering tracking

采用"当前"统计模型、匀加速模型以及匀速模型,运用交互式多模型算法的思想,提出了一种用于机动目标跟踪的交互式多模型自适应滤波算法.基本思路是上述三种模型并行工作,利用马尔可夫切换系数在它们之间进行切换,目标状态估计是上述三种模型交互作用的结果.蒙特卡罗结果表明该算法不仅克服了上述三种模型各自的缺点,提高了对机动目标的跟踪精度,同时具有全面自适应跟踪能力.

2004

0.0

0.914

. 2004, 16(4):767-771

Model sets interacting algorithm for maneuvering target tracking in the presence of glint noise

给出了一种量测噪声为闪烁噪声情况下的模型集交互机动目标跟踪算法.在雷达目标跟踪系统中由于目标位置的随机摆动,使得对其位置的量测伴随着闪烁噪声的出现,这种闪烁噪声会对目标跟踪的性能产生很大的影响.本文通过对闪烁噪声的分析,利用高斯分布和拉普拉斯分布的合成对其进行建模,在机动目标跟踪中采用两个模型集来处理闪烁噪声的情况,并详细推导了模型集交互时机动目标跟踪算法.最后,通过Monte Carlo的仿真结果表明了该算法的有效性.

2004

0.343

0.0

2005

0.0

2010

0.0

... 1 描述目标运动的常加速度模型在建立目标运动模型时,一般不考虑目标的形状而将其视为空间中一个点,并基于牛顿运动定律对目标运动规律进行描述^[18],其模型如下: ...

... 与飞机等飞行物相比,路面行驶车辆的车速变化较为缓慢,常规行驶时侧纵向加速度变化较小,为此本文采用表征机动性不大的目标运动过程的CA模型来描述前方目标的运动^[18] ...

2011

0.0

... ,v为目标的速度矢量或者速度矢量的幅值^[19] ...