基于故障在线估计的可重构机械臂分散容错控制

引用本文

赵博, 李成浩, 李元春. 基于故障在线估计的可重构机械臂分散容错控制. 44(6): 1729-1735
ZHAO Bo, LI Cheng-hao, LI Yuan-chun. Online fault estimation based on decentralized fault-tolerant control for reconfigurable manipulators. Journal of Jilin University Engineering and Technology Edition, 44(6): 1729-1735 复制到剪切板

Permissions

基于故障在线估计的可重构机械臂分散容错控制

赵博^1,³, 李成浩^2,³, 李元春^1,³

1.长春工业大学电气与电子工程学院, 长春 130012

2. 一汽轿车股份有限公司产品部, 长春 130012

3. 吉林大学通信工程学院, 长春 130022

通信作者:李元春(1962-),男,教授,博士生导师.研究方向:智能机械与机器人控制.E-mail:liyc@mail.ccut.edu.cn

作者简介:赵博(1987-),男,博士研究生.研究方向:智能机械与机器人控制.E-mail:zhaob09@mails.jlu.edu.cn

基金:国家自然科学基金项目(61374051,60974010); 吉林省科技发展计划项目(20110705);

摘要

为了降低可重构机械臂模块关节执行器和传感器故障对其控制性能的影响,提出了一种基于故障在线估计的分散容错控制方法。基于可重构机械臂的模块化属性和Lyapunov稳定性理论,设计了分散自适应滑模观测器以实现执行器和传感器故障的在线自适应估计。同时采用神经网络对子系统非线性项进行逼近和补偿,并结合非奇异快速Terminal滑模思想实现了分散容错控制。最后,采用两种不同构形的三自由度可重构机械臂进行了仿真试验,结果表明,所设计的容错控制方法是有效的。

关键词: 自动控制技术; 可重构机械臂; 故障在线估计; 分散滑模观测器; 容错控制

中图分类号:TP24 文献标志码:A 文章编号:1671-5497(2014)06-1729-07

Online fault estimation based on decentralized fault-tolerant control for reconfigurable manipulators

ZHAO Bo^1,³, LI Cheng-hao^2,³, LI Yuan-chun^1,³

1.College of Electrical and Electronic Engineering, Changchun University of Technology, Changchun 130012, China

2.Product Development Department, FAW Car Co., Ltd, Changchun 130012, China

3.College of Communication Engineering,Jilin University,Changchun 130022, China

Abstract

To reduce the influence of module joint actuator and sensor failure on the controllability of the reconfigurable manipulator, an online fault estimation method based on the decentralized fault-tolerant control scheme was proposed. Based on the modularized property of the manipulator and Lyapunov stability theory, a decentralized adaptive sliding mode observer is constructed to estimate the actuator and sensor faults adaptively. Meanwhile, the nonlinear terms are approximated or compensated by neural networks. Then, the idea of non-singular fast terminal mode control was employed to achieve decentralized fault-tolerant control. Finally, numerical simulation was carried out for two 3-DOF reconfigurable manipulators with different configurations. The results demonstrate the effectiveness of the proposed fault-tolerant control scheme.

Keyword: automatic control technique; reconfigurable manipulators; online fault estimation; decentralized adaptive sliding mode observer; fault tolerant control

Show Figures

0 引言

可重构机械臂^{[ 1]}因其易于对模块进行增减和互换,在航空航天、精密制造、高危作业以及军事战场等复杂环境中有着广泛的应用前景。长时间的工作会导致执行器和传感器不可避免地发生故障,若得不到及时处理,可重构机械臂会以不可预知的方式运行,给生产生活甚至生命安全带来巨大危害,因此亟需针对其进行故障诊断和容错控制的研究。目前,针对此问题,解决方法主要有基于解析模型^{[ 2, 3, 4]}、基于信号处理^{[ 5, 6, 7]}及基于知识挖掘^{[ 8, 9, 10]}等。但是现有针对故障诊断和容错控制的研究一般只针对执行器或传感器单一元件故障进行,对二者同时故障的情况考虑不多。

基于此,本文提出了基于故障在线估计的分散控制方法,考虑了执行器和传感器同时故障的情况,将故障隔离在子系统中,使系统不论发生何种故障,故障关节性能的下降都不影响正常关节的控制性能,且可在不改变控制参数的条件下应用于不同构形的可重构机械臂中。

1 问题描述

可重构机械臂子系统动力学模型可描述为^{[ 11]}:

$\begin{matrix} \begin{matrix} M_{i} (q_{i}) {\overset{\cdot \cdot}{q}}_{i} + C_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) {\overset{\cdot}{q}}_{i} + \\ G_{i} (q_{i}) + Z_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) = u_{i} (1) \\ Z_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) = \\ \{\overset{n}{\sum_{j = 1, j \neq i}} M_{ij} (q) {\overset{\cdot \cdot}{q}}_{j} + [M_{ii} (q) - M_{i} (q_{i})] {\overset{\cdot \cdot}{q}}_{i}\} + \\ \{\overset{n}{\sum_{j = 1, j \neq i}} C_{ij} (q, \overset{\cdot}{q}) {\overset{\cdot}{q}}_{j} + [C_{ii} (q, \overset{\cdot}{q}) - \\ C_{i} (q_{i}, {\overset{\cdot}{q}}_{i})] {\overset{\cdot}{q}}_{i}\} + [{\bar{G}}_{i} (q) - G_{i} (q_{i})] (2) \end{matrix} \end{matrix}$

式中: Z_i( q, $\begin{matrix} \overset{\cdot}{q} \end{matrix}$ , $\begin{matrix} \overset{\cdot \cdot}{q} \end{matrix}$ )∈ R为子系统交联项。

设 x_i=[ x_i₁ x_i₂]^T =[ q_i $\begin{matrix} {\overset{\cdot}{q}}_{i} \end{matrix}$ ]^T( i=1,2,…, n),则当第 i个子系统执行器或传感器发生故障时,结合式(1)与子系统故障函数f_ia及f_is,式(2)可表示为状态空间的形式:

$\begin{matrix} S_{if} : \{\begin{matrix} {\overset{\cdot}{x}}_{i} = A_{i} x_{i} + B_{i} [g_{i} (q_{i}) (u_{i} + f_{ia} (q_{i}, {\overset{\cdot}{q}}_{i}, u_{i})) + \\ f_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) + h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q})] \\ y_{i} = C_{i} (x_{i} + f_{is}) \end{matrix} (3) \end{matrix}$

式中: x_i、 y_i分别为子系统 S_if的状态向量和输出向量,且:

$\begin{matrix} \begin{matrix} A_{i} = [\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix}]; B_{i} = [\begin{matrix} 0 \\ 1 \end{matrix}]; C_{i} = [\begin{matrix} 1 & 0 \end{matrix}] \\ \{\begin{matrix} f_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) = M_{i}^{- 1} (q_{i}) [- C_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) {\overset{\cdot}{q}}_{i} - G_{i} (q_{i})] \\ g_{i} (q_{i}) = M_{i}^{- 1} (q_{i}) \\ h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) = - M_{i}^{- 1} (q_{i}) Z_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) \\ f_{ia} (q_{i}, {\overset{\cdot}{q}}_{i}, u_{i}) = α (t - T_{ia}) ψ_{i} (q_{i}, {\overset{\cdot}{q}}_{i}, u_{i}) \end{matrix} (4) \end{matrix} \end{matrix}$

式中: α( t-T_ia)为单位阶跃函数, T_ia为子系统 i执行器故障发生时间; ψ_i( q_i, $\begin{matrix} {\overset{\cdot}{q}}_{i} \end{matrix}$ , u_i)为执行器故障函数;本文仅考虑模块关节位置传感器故障,则 f_is= $\begin{matrix} {[\begin{matrix} f_{is 1} & 0 \end{matrix}]}^{T} \end{matrix}$ 为子系统传感器故障函数矩阵,且满足‖ f_is( t)‖≤ ρ_i( t),其中 ρ_i( t)为已知连续函数。

本文的控制目标是针对故障子系统模型(3)设计基于故障在线估计的分散容错控制律,使可重构机械臂关节模块无论执行器发生故障,还是传感器发生故障,关节位置均能跟踪期望轨迹。

2 分散容错控制器设计

2.1 分散自适应滑模观测器设计

假设1 期望轨迹 y_ir, $\begin{matrix} {\overset{\cdot}{y}}_{ir} \end{matrix}$ 和 $\begin{matrix} {\overset{\cdot \cdot}{y}}_{ir} \end{matrix}$ 有界。

假设2 子系统的执行器故障 f_ia和传感器故障 f_is₁均有未知上界:‖ f_ia‖≤ $\begin{matrix} f_{ia}^{*} \end{matrix}$ ;‖ f_is₁‖≤ $\begin{matrix} f_{is}^{*} \end{matrix}$ 。

首先利用李代数方法进行线性变换^{[ 4]},将关节传感器故障转化为伪执行器故障,并引入一个一阶滤波器 z_i作为新的状态变量,即:

$\begin{matrix} {\overset{\cdot}{z}}_{i} = - a_{i} z_{i} + b_{i} y_{i 1} (5) \end{matrix}$

式中: y_i₁为关节位置传感器输出信号; a_i, b_i为常数,且 a_i>0, b_i≠0。

将式(3)中的输出方程代入式(5)中,可得:

$\begin{matrix} {\overset{\cdot}{z}}_{i} = - a_{i} z_{i} + b_{i} x_{i 1} + b_{i} f_{is 1} (6) \end{matrix}$

令 $\begin{matrix} {\bar{x}}_{i} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} x_{i 1} & x_{i 2} & x_{i 3} \end{matrix}]}^{T} \end{matrix}$ = $\begin{matrix} {[\begin{matrix} q_{i} & {\overset{\cdot}{q}}_{i} & z_{i} \end{matrix}]}^{T} \end{matrix}$ ,则扩展后的故障子系统模型可描述为:

$\begin{matrix} \begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{i 1} = x_{i 2} \\ {\overset{\cdot}{x}}_{i 2} = f_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) + g_{i} (q_{i}) (u_{i} + \\ f_{ia} (q_{i}, {\overset{\cdot}{q}}_{i}, u_{i})) + h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) \\ {\overset{\cdot}{x}}_{i 3} = b_{i} x_{i 1} - a_{i} x_{i 3} + b_{i} f_{is 1} \\ y_{i} = x_{i 3} \end{matrix} \\ (7) \end{matrix} \end{matrix}$

设计分散自适应滑模观测器如下:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{\hat{x}}}_{i 1} = {\hat{x}}_{i 2} + υ_{i 1} \\ {\overset{\cdot}{\hat{x}}}_{i 2} = {\hat{f}}_{i} ({\hat{q}}_{i}, {\overset{\cdot}{\hat{q}}}_{i}, {\hat{θ}}_{if}) + {\hat{g}}_{i} ({\hat{q}}_{i}, {\hat{θ}}_{ig}) u_{i} + \\ ν_{i} (e_{i 2}, {\hat{θ}}_{ip}) + υ_{i 2} + {\hat{δ}}_{i} \\ {\overset{\cdot}{\hat{x}}}_{i 3} = b_{i} {\hat{x}}_{i 1} - a_{i} {\hat{x}}_{i 3} + b_{i} {\hat{f}}_{is 1} + υ_{i 3} \\ {\hat{y}}_{i} = {\hat{x}}_{i 3} \end{matrix} (8) \end{matrix}$

式中: υ_ij=κ_ij $\begin{matrix} \frac{x_{ij} - {\hat{x}}_{ij}}{‖ x_{ij} - {\hat{x}}_{ij} ‖} \end{matrix}$ , j=1,2,3; $\begin{matrix} {\hat{δ}}_{i} \end{matrix}$ 用于补偿神经网络估计误差对控制精度的影响。

定义观测误差为 e_ij=x_ij- $\begin{matrix} {\hat{x}}_{ij} \end{matrix}$ , j=1,2,3。由式(7)(8)可得相应的误差动力学方程为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{e}}_{i 1} = e_{i 2} - υ_{i 1} \\ {\overset{\cdot}{e}}_{i 2} = (f_{i} - {\hat{f}}_{i}) + (g_{i} - {\hat{g}}_{i}) u_{i} + h_{i} - ν_{i} + \\ g_{i} f_{ia} - υ_{i 2} - {\hat{δ}}_{i} \\ {\overset{\cdot}{e}}_{i 3} = b_{i} e_{i 1} - a_{i} e_{i 3} + b_{i} (f_{is 1} - {\hat{f}}_{is 1}) - υ_{i 3} \end{matrix} (9) \end{matrix}$

采用RBF神经网络 $\begin{matrix} {\hat{f}}_{i} \end{matrix}$ ( $\begin{matrix} {\hat{q}}_{i} \end{matrix}$ , $\begin{matrix} {\overset{\cdot}{\hat{q}}}_{i} \end{matrix}$ )和 $\begin{matrix} {\hat{g}}_{i} \end{matrix}$ ( $\begin{matrix} {\hat{q}}_{i} \end{matrix}$ )对系统的不确定项 f_i( q_i, $\begin{matrix} {\overset{\cdot}{q}}_{i} \end{matrix}$ )和 g_i( q_i)进行估计,理想神经网络逼近如下所示:

$\begin{matrix} \begin{matrix} f_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) = {θ^{T}}_{if} σ_{if} (q_{i}, {\overset{\cdot}{q}}_{i}) + ε_{if} (10) \\ g_{i} (q_{i}) = {θ^{T}}_{ig} σ_{ig} (q_{i}) + ε_{ig} (11) \\ {\hat{f}}_{i} ({\hat{q}}_{i}, {\overset{\cdot}{\hat{q}}}_{i}) = {\hat{θ}}^{T}_{if} {\hat{σ}}_{if} ({\hat{q}}_{i}, {\overset{\cdot}{\hat{q}}}_{i}) (12) \\ {\hat{g}}_{i} ({\hat{q}}_{i}) = {\hat{θ}}^{T}_{ig} {\hat{σ}}_{ig} ({\hat{q}}_{i}) (13) \end{matrix} \end{matrix}$

定义 $\begin{matrix} {\hat{θ}}_{if} \end{matrix}$ 和 $\begin{matrix} {\hat{θ}}_{ig} \end{matrix}$ 分别为理想神经网络权值 θ_if和 θ_ig的估计值; $\begin{matrix} {\tilde{θ}}_{if} \end{matrix}$ = $\begin{matrix} {\hat{θ}}_{if} \end{matrix}$ -θ_if和 $\begin{matrix} {\tilde{θ}}_{ig} \end{matrix}$ = $\begin{matrix} {\hat{θ}}_{ig} \end{matrix}$ -θ_ig为估计误差。

假设3 关联项 h_i( q, $\begin{matrix} \overset{\cdot}{q} \end{matrix}$ , $\begin{matrix} \overset{\cdot \cdot}{q} \end{matrix}$ )有界且满足^{[ 12]}:

$\begin{matrix} |h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q})| \leq \overset{n}{\sum_{j = 1}} d_{ij} E_{j} (14) \end{matrix}$

式中: d_ij≥0为未知常数; E_j=1 + $\begin{matrix} |e_{i 2}| \end{matrix}$ + $\begin{matrix} {|e_{i 2}|}^{2} \end{matrix}$ 。

采用RBF神经网络 ν_i( e_i₂, $\begin{matrix} {\hat{θ}}_{ip} \end{matrix}$ )补偿交联项对系统的影响:

$\begin{matrix} ν_{i} (e_{i 2}, {\hat{θ}}_{ip}) = sgn (e_{i 2}) {\hat{θ}}_{ip} {\hat{σ}}_{ip} (|e_{i 2}|) (15) \end{matrix}$

式中: $\begin{matrix} {\hat{θ}}_{ip} \end{matrix}$ 为权值 θ_ip的估计值, $\begin{matrix} {\hat{σ}}_{ip} \end{matrix}$ 为神经网络基函数 σ_ip的估计值。定义 $\begin{matrix} {\tilde{θ}}_{ip} \end{matrix}$ = $\begin{matrix} {\hat{θ}}_{ip} \end{matrix}$ -θ_ip为权值估计误差; $\begin{matrix} {\tilde{σ}}_{ip} \end{matrix}$ = $\begin{matrix} {\hat{σ}}_{ip} \end{matrix}$ -σ_ip为估计误差。

定义神经网络最小估计误差如下:

$\begin{matrix} \begin{matrix} ω_{i 1} = {θ^{T}}_{if} ({\hat{σ}}_{if} ({\hat{q}}_{i}, {\overset{\cdot}{\hat{q}}}_{i}) - σ_{if} (q_{i}, {\overset{\cdot}{q}}_{i})) + ε_{if} + ε_{ig} u_{i} + \\ {θ^{T}}_{ig} ({\hat{σ}}_{ig} ({\hat{q}}_{i}) - σ_{ig} (q_{i})) u_{i} + (g_{i} - {\hat{g}}_{i}) f_{ia} \\ (16) \\ ω_{i 2} = R_{i} (|e_{i 2}|) - {θ^{T}}_{ip} {\hat{σ}}_{ip} (|e_{i 2}|) (17) \end{matrix} \end{matrix}$

式中: R_i( $\begin{matrix} |e_{i 2}| \end{matrix}$ ) =n $\begin{matrix} \max_{ij} \end{matrix} \begin{matrix} \{d_{ij}\} \end{matrix}$ E_i,逼近误差 ε_if和 ε_ig未知有界,且满足:

$\begin{matrix} ω_{i} = |ω_{i 1}| + |ω_{i 2}| (18) \end{matrix}$

定理1 当可重构机械臂子系统发生执行器或传感器故障时,由分散自适应滑模观测器式(8)与子系统的状态空间方程式(7)得到误差动力学方程式(9),结合假设2和假设3,并且采用式(19)~(23)所示的自适应更新律,能够在线估计出执行器和传感器故障,并且使状态观测误差 e_i在有限时间内按指数规律收敛,即估计状态 $\begin{matrix} {\hat{x}}_{i} \end{matrix}$ 渐近收敛到实际状态 x_i。

神经网络权值 $\begin{matrix} {\hat{θ}}_{if} \end{matrix}$ , $\begin{matrix} {\hat{θ}}_{ig} \end{matrix}$ , $\begin{matrix} {\hat{θ}}_{ip} \end{matrix}$ 和故障估计参数 $\begin{matrix} {\hat{f}}_{is 1} \end{matrix}$ , $\begin{matrix} {\hat{δ}}_{i} \end{matrix}$ 分别按下面的自适应律更新:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{\hat{θ}}}_{if} = - η_{if} e_{i 2} {\hat{σ}}_{if} (19) \\ {\overset{\cdot}{\hat{θ}}}_{ig} = - η_{ig} e_{i 2} {\hat{σ}}_{ig} (q_{i}) u_{i} (20) \\ {\overset{\cdot}{\hat{θ}}}_{ip} = - η_{ip} |e_{i 2}| {\hat{σ}}_{ip} (21) \\ {\overset{\cdot}{\hat{f}}}_{is 1} = η_{is} b e_{i 3} (22) \\ {\overset{\cdot}{\hat{δ}}}_{i} = λ_{i} e_{i 2} (23) \end{matrix} \end{matrix}$

式中: η_if、 η_ig、 η_ip、 η_is、 λ_i均为正的常数,且子系统传感器故障可由式(22)自适应估计得到。

考虑式(8)中 ν_i₂的表达结构,选择合适的正常数 σ_i,使得当 κ_i₂ > $\begin{matrix} f_{ia}^{*} \end{matrix}$ 满足时,输出等效误差可由式(24)任意精度估计^{[ 4]}:

$\begin{matrix} υ_{i 2 σ} = κ_{i 2} \frac{x_{i 2} - {\hat{x}}_{i 2}}{‖ x_{i 2} - {\hat{x}}_{i 2} ‖+ σ_{i}} (24) \end{matrix}$

则子系统执行器故障可由式(25)得到。

$\begin{matrix} {\hat{f}}_{ia} = i^{- 1} υ_{i 2 σ} (25) \end{matrix}$

证明选取Lyapunov函数如下:

$\begin{matrix} V_{i} = V_{i 1} + V_{i 2} + V_{i 3} (26) \end{matrix}$

步骤1 选取Lyapunov函数:

$\begin{matrix} V_{i 1} = \frac{1}{2} e_{i 1}^{2} (27) \end{matrix}$

其对时间的导数为:

$\begin{matrix} {\overset{\cdot}{V}}_{i 1} = e_{i 1} {\overset{\cdot}{e}}_{i 1} \leq |e_{i 1}| (|e_{i 2}| - κ_{i 1}) (28) \end{matrix}$

当 κ_i₁ >μ_i₁ + $\begin{matrix} |e_{i 2}| \end{matrix}$ 时,则 $\begin{matrix} {\overset{\cdot}{V}}_{1} \end{matrix}$ ≤ $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ ( -μ_i₁ $\begin{matrix} |e_{i 1}| \end{matrix}$ ) <0,其中 μ_i₁为小的正常数。

步骤2 令 $\begin{matrix} {\tilde{f}}_{is} \end{matrix}$ =f_is- $\begin{matrix} {\hat{f}}_{is} \end{matrix}$ ,选取Lyapunov函数:

$\begin{matrix} V_{i 3} = \frac{1}{2} e_{i 3}^{2} + \frac{1}{2 η_{is}} {\tilde{f}}_{is 1}^{2} (29) \end{matrix}$

其对时间的导数为:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{V}}_{i 3} = e_{i 3} {\overset{\cdot}{e}}_{i 3} + η_{is}^{- 1} {\tilde{f}}_{is 1} {\overset{\cdot}{\tilde{f}}}_{is 1} = \\ e_{i 3} (- a_{i} e_{i 3} + b_{i} e_{i 1} + b_{i} e_{is} - υ_{i 3}) - η_{is}^{- 1} {\tilde{f}}_{is 1} {\overset{\cdot}{\hat{f}}}_{is 1} = \\ - a_{i} e_{i 3}^{2} + b_{i} e_{i 1} e_{i 3} - κ_{i 3} e_{i 3} sgn (e_{i 3}) + \\ e_{is} (b_{i} e_{i 3} - η_{is}^{- 1} {\tilde{f}}_{is 1} {\overset{\cdot}{\hat{f}}}_{is 1}) \leq \\ - a_{i} e_{i 3}^{2} + |e_{i 3}| (b_{i} |e_{i 1}| - κ_{i 3}) (30) \end{matrix} \end{matrix}$

当 κ_i₃ >b_i $\begin{matrix} |e_{i 1}| \end{matrix}$ +μ_i₃时, $\begin{matrix} {\overset{\cdot}{V}}_{3} \end{matrix}$ ≤ $\begin{matrix} \overset{n}{\sum_{i = 1}} \end{matrix}$ ( -a_i $\begin{matrix} e_{i 3}^{2} \end{matrix}$ -μ_i₃ $\begin{matrix} |e_{i 3}| \end{matrix}$ )≤0,其中 μ_i₃为正小常数。

步骤3 令 $\begin{matrix} {\tilde{f}}_{ia} \end{matrix}$ =f_ia- $\begin{matrix} {\hat{f}}_{ia} \end{matrix}$ ,选取Lyapunov函数:

$\begin{matrix} \begin{matrix} V_{i 2} = \frac{1}{2} e_{i 2}^{2} + \frac{1}{2 η_{if}} {\tilde{θ}}^{T}_{if} {\tilde{θ}}_{if} + \frac{1}{2 η_{ig}} {\tilde{θ}}^{T}_{ig} {\tilde{θ}}_{ig} + \\ \frac{1}{2 η_{ip}} {\tilde{θ}}^{T}_{ip} {\tilde{θ}}_{ip} + \frac{1}{2 λ_{i}} {\tilde{δ}}^{T}_{i} {\tilde{δ}}_{i} (31) \end{matrix} \end{matrix}$

其对时间的导数为:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{V}}_{i 2} = e_{i 2} ((f_{i} - {\hat{f}}_{i}) + (g_{i} - {\hat{g}}_{i}) u_{i} + h_{i} - ν_{i} + \\ g_{i} f_{ia} - υ_{i 2} - {\hat{δ}}_{i}) + \frac{1}{η_{if}} {\tilde{θ}}_{if} {\overset{\cdot}{\hat{θ}}}_{if} + \frac{1}{η_{ig}} {\tilde{θ}}_{ig} {\overset{\cdot}{\hat{θ}}}_{ig} + \\ \frac{1}{η_{ip}} {\tilde{θ}}_{ip} {\overset{\cdot}{\hat{θ}}}_{ip} - \frac{1}{λ_{i}} {\tilde{δ}}^{T}_{i} {\overset{\cdot}{\hat{δ}}}_{i} \leq \\ |e_{i 2}| {\hat{θ}}_{ip} {\hat{σ}}_{ip} + |e_{i 2}| |ω_{1}| - e_{i 2} {\hat{δ}}_{i} + \frac{1}{η_{ip}} {\tilde{θ}}_{ip} {\overset{\cdot}{\hat{θ}}}_{ip} - \\ \frac{1}{λ_{i}} {\tilde{δ}}^{T}_{i} {\overset{\cdot}{\hat{δ}}}_{i} + \max_{ij} \{d_{ij}\} \overset{n}{\sum_{i = 1}} |e_{i 2}| \overset{n}{\sum_{j = 1}} E_{j} (32) \end{matrix} \end{matrix}$

考虑假设3,并注意到 $\begin{matrix} |e_{i 2}| \end{matrix}$ ≤ $\begin{matrix} |e_{j 2}| \end{matrix}$ ⇔ E_i≤ E_j,应用Chebyshev不等式,可得:

$\begin{matrix} \overset{n}{\sum_{i = 1}} |e_{i 2}| \overset{n}{\sum_{j = 1}} E_{j} \leq n \overset{n}{\sum_{i = 1}} |e_{i 2}| E_{i} (33) \end{matrix}$

定义 $\begin{matrix} {\tilde{δ}}_{i} \end{matrix}$ =δ_i- $\begin{matrix} {\hat{δ}}_{i} \end{matrix}$ ,将式(23)(33)代入式(32)可得:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{V}}_{2} \leq \overset{n}{\sum_{i = 1}} (|e_{i 2}| (n \underset{ij}{\max \{d_{ij}\}} E_{i} - {\hat{θ}}_{ip} {\hat{σ}}_{ip}) + \\ |e_{i 2}| |ω_{i 1}| - e_{i 2} {\hat{δ}}_{i} + \frac{1}{η_{ip}} {\tilde{θ}}_{ip} {\overset{\cdot}{\hat{θ}}}_{ip} - \frac{1}{λ_{i}} {\tilde{δ}}^{T}_{i} {\hat{δ}}_{i}) \leq \\ \overset{n}{\sum_{i = 1}} (e_{i 2} (δ_{i} - {\hat{δ}}_{i}) - \frac{1}{λ_{i}} {\tilde{δ}}^{T}_{i} {\hat{δ}}_{i}) = 0 (34) \end{matrix} \end{matrix}$

由上述各步骤结论及式(26)对时间的导数可知:

$\begin{matrix} \overset{\cdot}{V} = \overset{n}{\sum_{i = 1}} ({\overset{\cdot}{V}}_{i 1} + {\overset{\cdot}{V}}_{i 2} + {\overset{\cdot}{V}}_{i 3}) < 0 (35) \end{matrix}$

由Lyapunov稳定性理论和Barbalat引理可知:状态观测误差 e_i将在有限时间内按指数规律收敛到零点,即估计状态 $\begin{matrix} {\hat{x}}_{i} \end{matrix}$ 将渐近收敛到实际状态 x_i。

2.2 基于非奇异快速Terminal滑模的分散容错控制

为了使可重构机械臂系统发生故障时关节轨迹仍能精确地跟踪期望轨迹,本节设计了一种基于非奇异Terminal滑模的分散容错控制器。此方法可在系统发生故障时改善控制性能,并且避免了传统Terminal滑模控制可能导致的奇异现象。

定义位置跟踪误差为:

$\begin{matrix} \begin{matrix} e_{i} = {\hat{x}}_{i 1} - y_{id} (36) \\ 则其导数为 : {\overset{\cdot}{e}}_{i} = {\overset{\cdot}{\hat{x}}}_{i 1} - {\overset{\cdot}{y}}_{id} (37) \end{matrix} \end{matrix}$

定义非奇异快速Terminal滑模面为:

$\begin{matrix} s_{i} = e_{i} + α_{i}^{- 1} e_{i}^{k_{i} / l_{i}} + β_{i}^{- 1} i^{p_{i} / q_{i}} (38) \end{matrix}$

式中: α_i>0, β_i>0; p_i, q_i, k_i, l_i为正奇数,且满足1 <p_i/q_i<2, k_i/l_i>p_i/q_i。

式(38)对时间的导数为:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{s}}_{i} = {\overset{\cdot}{e}}_{i} + \frac{1}{α_{i}} \frac{k_{i}}{l_{i}} e_{i}^{k_{i} / l_{i} - 1} {\overset{\cdot}{e}}_{i} + \frac{1}{β_{i}} \frac{p_{i}}{q_{i}} i^{p_{i} / q_{i} - 1} {\overset{\cdot \cdot}{e}}_{i} = \\ {\overset{\cdot}{e}}_{i} + \frac{1}{α_{i}} \frac{k_{i}}{l_{i}} e_{i}^{k_{i} / l_{i} - 1} {\overset{\cdot}{e}}_{i} + \frac{1}{β_{i}} \frac{p_{i}}{q_{i}} i^{p_{i} / q_{i} - 1} [{\hat{f}}_{i} ({\hat{q}}_{i}, {\overset{\cdot}{\hat{q}}}_{i}) + \\ {\hat{g}}_{i} ({\hat{q}}_{i}) u_{i} + ν_{i} (e_{i 2}, {\hat{θ}}_{ip}) + υ_{i 2} + {\hat{δ}}_{i} - {\overset{\cdot \cdot}{y}}_{id}] \\ (39) \end{matrix} \end{matrix}$

基于非奇异快速Terminal滑模的分散容错控制律设计为:

$\begin{matrix} \begin{matrix} u_{i} = - \frac{1}{{\hat{g}}_{i} ({\hat{q}}_{i})} ({\hat{f}}_{i} ({\hat{q}}_{i}, {\overset{\cdot}{\hat{q}}}_{i}) + υ_{i 2} + ν_{i} (e_{i 2}, {\hat{θ}}_{ip}) + \\ {\hat{δ}}_{i} - {\overset{\cdot \cdot}{y}}_{id} + β_{i} \frac{q_{i}}{p_{i}} {\overset{\cdot}{e}}_{i}^{2 - p_{i} / q_{i}} (1 + \frac{k_{i}}{α_{i} l_{i}} e_{i}^{k_{i} / l_{i} - 1}) + \\ ζ_{i} s_{i} + η_{i} sgn (s_{i})) (40) \end{matrix} \end{matrix}$

定理2 考虑含有故障的子系统动力学模型式(7),设计了如式(8)所示的基于RBF神经网络的分散自适应滑模观测器,应用式(40)所示的基于非奇异Terminal滑模分散容错控制律、式(19)~(23)所示的自适应更新律以及式(25)所示的故障辨识函数,则可重构机械臂的轨迹跟踪误差将在有限时间收敛到零,从而实现故障容错的目的。

证明选取Lyapunov函数如下:

$\begin{matrix} V_{i} = \frac{1}{2} s_{i}^{2} (41) \end{matrix}$

式(41)对时间的导数为:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{V}}_{i} = s_{i} {\overset{\cdot}{s}}_{i} = \\ s_{i} {{\overset{\cdot}{e}}_{i} + \frac{1}{α_{i}} \frac{k_{i}}{l_{i}} e_{i}^{k_{i} / l_{i} - 1} {\overset{\cdot}{e}}_{i} + \frac{1}{β_{i}} \frac{p_{i}}{q_{i}} {\overset{\cdot}{e}}_{i}^{p_{i} / q_{i} - 1} [{\hat{f}}_{i} ({\hat{q}}_{i}, {\overset{\cdot}{\hat{q}}}_{i}) + \\ {\hat{g}}_{i} ({\hat{q}}_{i}) u_{i} + ν_{i} (e_{i 2}, {\hat{θ}}_{ig}) + υ_{i 2} + {\hat{δ}}_{i} - {\overset{\cdot \cdot}{y}}_{id}]} \\ (42) \end{matrix} \end{matrix}$

将式(40)代入式(42),可得:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{V}}_{i} = \frac{1}{β_{i}} \frac{p_{i}}{q_{i}} {\overset{\cdot}{e}}_{i}^{p_{i} / q_{i} - 1} s_{i} (- ζ_{i} s_{i} - η_{i} sgn (s_{i})) = \\ \frac{1}{β_{i}} \frac{p_{i}}{q_{i}} {\overset{\cdot}{e}}_{i}^{p_{i} / q_{i} - 1} (- ζ_{i} s_{i}^{2} - η_{i} |s_{i}|) (43) \end{matrix} \end{matrix}$

可见,当 s_i≠0时,由于1 < $\begin{matrix} \frac{p_{i}}{q_{i}} \end{matrix}$ <2,则0 < $\begin{matrix} \frac{p_{i}}{q_{i}} \end{matrix}$ -1 <1,又由于 β_i>0, p_i和 q_i为正奇数,因此:

(1)当 $\begin{matrix} {\overset{\cdot}{e}}_{i} \end{matrix}$ ≠0时, ξ_i= $\begin{matrix} \frac{1}{β_{i}} \end{matrix} \begin{matrix} \frac{p_{i}}{q_{i}} \end{matrix} \begin{matrix} {\overset{\cdot}{e}}_{i}^{p_{i} / q_{i} - 1} \end{matrix}$ >0, $\begin{matrix} {\overset{\cdot}{V}}_{i} \end{matrix}$ ≤ -ξ_i( ζ_i $\begin{matrix} s_{i}^{2} \end{matrix}$ +η_i $\begin{matrix} |s_{i}| \end{matrix}$ )≤0。

这表明 V_i( t)≤ V_i(0),因此 s_i是有界的。设函数 Φ_i( t) =ξ_i( ζ_i $\begin{matrix} s_{i}^{2} \end{matrix}$ +η_i $\begin{matrix} |s_{i}| \end{matrix}$ )≤ - $\begin{matrix} {\overset{\cdot}{V}}_{i} \end{matrix}$ ,对 Φ_i( t)从0到 t积分得 $\begin{matrix} \int_{0}^{t} \end{matrix}$ Φ_i( τ)d τ≤ $\begin{matrix} \int_{0}^{t} \end{matrix} \begin{matrix} {\overset{\cdot}{V}}_{i} \end{matrix}$ d τ=V_i(0) -V_i( t)。由于 V_i(0)有界, V_i( t)非增,有下界,可得 $\begin{matrix} \lim_{t \to \infty} \end{matrix} \begin{matrix} \int_{0}^{t} \end{matrix}$ Φ_i( τ)d τ<¥,因此可知 Φ_i( t)∈ L₂,由于 Φ_i( t)∈ $\begin{matrix} L_{\infty} \end{matrix}$ ,根据Barbalat引理可得 $\begin{matrix} \lim_{t \to \infty} \end{matrix}$ Φ_i( t) =0,进而得到 $\begin{matrix} \lim_{t \to \infty} \end{matrix}$ s_i=0,即跟踪误差 e_i= $\begin{matrix} {\hat{x}}_{i 1} \end{matrix}$ -y_id也将在有限时间内收敛到零。

(2)当 $\begin{matrix} {\overset{\cdot}{e}}_{i} \end{matrix}$ =0时, $\begin{matrix} {\overset{\cdot}{V}}_{i} \end{matrix}$ =0。但 $\begin{matrix} {\overset{\cdot}{e}}_{i} \end{matrix}$ =0, e_i≠0,易证明其并不是稳定的状态, $\begin{matrix} {\overset{\cdot}{V}}_{i} \end{matrix}$ =0不能一直保持,因此根据Lyapunov稳定性定理,系统将在有限时间到达并保持在非奇异终端滑模面 s_i=0上,跟踪误差 e_i也将在有限时间内收敛到零,因此定理2成立。

3 数值仿真

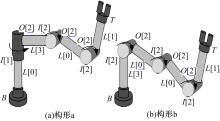
为了验证本文所设计的分散容错控制方法的有效性,采用如图1所示的两种不同构形的三自由度可重构机械臂进行数值仿真。

	Figure Option View Download New Window
	图1 三自由度可重构机械臂构形Fig.1 Configurations of 3-DOF reconfigurable manipulators

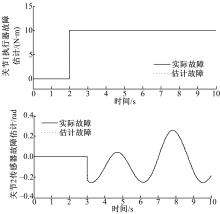
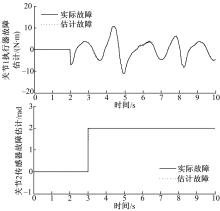
仿真中设初始位置为 $\begin{matrix} {\hat{q}}_{1} \end{matrix} \begin{matrix} (0) \end{matrix}$ = $\begin{matrix} {\hat{q}}_{2} \end{matrix} \begin{matrix} (0) \end{matrix}$ = $\begin{matrix} {\hat{q}}_{3} \end{matrix} \begin{matrix} (0) \end{matrix}$ =1,初始速度为 $\begin{matrix} {\overset{\cdot}{\hat{q}}}_{1} \end{matrix} \begin{matrix} (0) \end{matrix}$ = $\begin{matrix} {\overset{\cdot}{\hat{q}}}_{2} \end{matrix} \begin{matrix} (0) \end{matrix}$ = $\begin{matrix} {\overset{\cdot}{\hat{q}}}_{3} \end{matrix} \begin{matrix} (0) \end{matrix}$ =0,观测器参数为 κ_i₁ =κ_i₂ =κ_i₃ =10, σ_i=0 .02;控制器参数为 p_i=5, q_i=3, k_i=7, l_i=3, α_i=0 .05, β_i=0 .5, ζ_i=10, η_i=0 .001;自适应增益系数为 η_if=0 .02, η_ig=0 .01, η_ip=0 .01, η_is=10⁵, λ_i=1;滤波器参数为 a_i=1, b_i=1。

对于构形a,分别于 t=2 s和 t=3 s对关节1执行器、关节2传感器加入故障,故障函数如下:

f₁ _a= $\begin{matrix} \{\begin{matrix} 0, t < 2 \\ 10, t \geq 2 \end{matrix} \end{matrix}$ , f₂ _s= $\begin{matrix} \{\begin{matrix} 0, t < 3 \\ - 0.5 q_{2}, t \geq 3 \end{matrix} \end{matrix}$

图2为利用所设计分散自适应滑模观测器得到的故障估计曲线,可以看出此方法可精确地在线估计故障。

	Figure Option View Download New Window
	图2 构形a故障在线估计曲线Fig.2 Online fault estimation curves of configuration a

	Figure Option View Download New Window
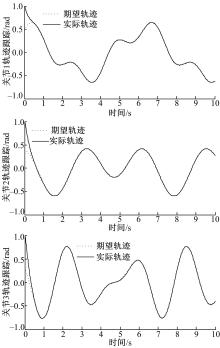	图3 构形a应用所设计容错控制律关节跟踪曲线Fig.3 Joints tracking curves applied the proposed fault tolerant control of configuration a

图3为在发生故障时,采用所设计的非奇异Terminal分散容错控制律得到的轨迹跟踪曲线,从图中可知,各子系统得到了满意的跟踪性能。

	Figure Option View Download New Window
	图4 构形b故障在线估计曲线Fig.4 Online fault estimation curves of configuration b

图4和图5是在不改变控制参数的条件下应用构形b进行相同的数值仿真的结果,其中故障函数如式(44)所示。

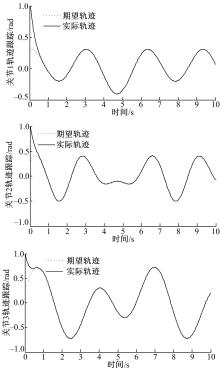$\begin{matrix} \{\begin{matrix} f_{1 a} = \{\begin{matrix} 0, t < 2 \\ 10 \sin (2 q_{1}) {\overset{\cdot}{q}}_{1}, t \geq 2 \end{matrix} \\ f_{2 s} = \{\begin{matrix} 0, t < 3 \\ 2, t \geq 3 \end{matrix} \end{matrix} (44) \end{matrix}$

	Figure Option View Download New Window
	图5 构形b应用所设计容错控制律关节跟踪曲线Fig.5 Joints tracking curves applied the proposed fault tolerant control of configuration b

从图4和图5可以看出:在不改变参数的条件下,所设计的控制方法仍然适用,因此所提方法可应用于具有不同构形、不同自由度的可重构机械臂。

4 结束语

针对由于可重构机械臂模块关节执行器和传感器故障而导致控制系统性能下降的问题,提出了一种基于故障在线隔离的分散容错控制方法。基于可重构机械臂的模块化属性,设计了分散自适应滑模观测器以实现执行器和传感器故障隔离,并结合非奇异Terminal滑模控制方法对子系统故障进行容错处理。此方法将故障隔离在子系统内,且可在不修改控制参数的条件下对不同构形的可重构机械臂实现容错控制。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Paredis C J J, Brown H B, Khosla P K. Rapidly deployable manipulator system[J]. Robotics and Autonomous Systems, 1997, 21(3): 289-304. [本文引用:1] [JCR: 1.156]
[2]	Brambilla D, Capisani L M, Ferrara A, et al. Fault detection for robot manipulators via second-order sliding modes[J]. IEEE Transactions on Industrial Electronics, 2008, 55(11): 3954-3963. [本文引用:1] [JCR: 5.165]
[3]	Yoo S J. Actuator fault detection and adaptive accommodation control of flexible-joint robots[J]. IET Control Theory and Applications, 2012, 6(10): 1497-1507. [本文引用:1] [JCR: 1.717]
[4]	Zhao B, Li Y C. Multisensor fault identification scheme based on decentralized sliding mode observers applied to reconfigurable manipulators[J]. Mathematical Problems in Engineering, 2013. DOI: 10.1155/2013/327916. [本文引用:2] [JCR: 1.383]
[5]	Zhang Y W, Ma C. Decentralized fault diagnosis using multiblock kernel independent component analysis[J]. Chemical Engineering Research and Design, 2012, 90(5): 667-676. [本文引用:1] [JCR: 1.927]
[6]	Yan R Q, Gao R X, Chen X F. Wavelets for fault diagnosis of rotary machines: A review with applications[J]. Signal Processing, 2014, 96(Part A): 1-15. [本文引用:1] [JCR: 1.851]
[7]	Subrahmanya N, Shin Y C. A data-based framework for fault detection and diagnostics of non-linear systems with partial state measurement[J]. Engineering Applications of Artificial Intelligence, 2013, 26(1): 446-455. [本文引用:1] [JCR: 1.625]
[8]	Zhao C L, Sun X B, Sun S L, et al. Fault diagnosis of sensor by chaos particle swarm optimization algorithm and support vector machine[J]. Expert Systems with Applications, 2011, 38(8): 9908-9912. [本文引用:1] [JCR: 1.854]
[9]	Silva J C D, Saxena A, Balaban E, et al. A knowledge-based system approach for sensor fault modeling, detection and mitigation[J]. Expert Systems with Applications, 2013, 39(12): 10977-10989. [本文引用:1] [JCR: 1.854]
[10]	Milena P, Rapaic M R, Jelicic Z D, et al. On-line adaptive clustering for process monitoring and fault detection[J]. Expert System with Applications, 2012, 39(11): 10226-10235. [本文引用:1] [JCR: 1.854]
[11]	李英, 朱明超, 李元春. 可重构机械臂模糊神经补偿控制[J]. 吉林大学学报: 工学版, 2007, 37(1): 206-211. Li Ying, Zhu Ming-chao, Li Yuan-chun. Neurofuzzy compensation control for reconfigurable manipulator[J]. Journal of Jilin University (Engineering and Technology Edition), 2007, 37(1): 206-211. [本文引用:1] [CJCR: 0.701]
[12]	Zhu M, Li Y. Decentralized adaptive fuzzy sliding mode control for reconfigurable modular manipulators[J]. International Journal of Robust and Nonlinear Control, 2010, 20(4): 472-488. [本文引用:1] [JCR: 1.9]

1997

1.156

0.0

. 1997, 21(3):null-null

Rapidly deployable manipulator system

... 0 引言可重构机械臂^[1]因其易于对模块进行增减和互换,在航空航天、精密制造、高危作业以及军事战场等复杂环境中有着广泛的应用前景 ...

2008

5.165

0.0

2012

1.717

0.0

2013

1.383

0.0

... 首先利用李代数方法进行线性变换^[4],将关节传感器故障转化为伪执行器故障,并引入一个一阶滤波器z_i作为新的状态变量,即: ...

... 满足时,输出等效误差可由式(24)任意精度估计^[4]: ...

2012

1.927

0.0

. 2012, 90(5):null-null

Decentralized fault diagnosis using multiblock kernel independent component analysis

2014

1.851

0.0

. 2014, 96(Part A):null-null

Wavelets for fault diagnosis of rotary machines: A review with applications

2013

1.625

0.0

. 2013, 26(1):null-null

A data-based framework for fault detection and diagnostics of non-linear systems with partial state measurement

2011

1.854

0.0

. 2011, 38(8):9908-9912 DOI:10.1016/j.eswa.2011.02.043

Fault diagnosis of sensor by chaos particle swarm optimization algorithm and support vector machine

Abstract

Fault diagnosis of sensor timely and accurately is very important to improve the reliable operation of systems. In the study, fault diagnosis of sensor by chaos particle swarm optimization algorithm and support vector machine is presented in the paper, where chaos particle swarm optimization is chosen to determine the parameters of SVM. Chaos particle swarm optimization is a kind of improved particle swarm optimization, which can not only avoid the search being trapped in local optimum and but also help to search the optimum quickly by using chaos queues. The wireless sensor is employed as research object, and its four fault types including shock, biasing, short circuit and shifting are applied to test the diagnostic ability of CPSO-SVM compared with other diagnostic methods. The diagnostic results show that CPSO-SVM has higher diagnostic accuracy of wireless sensor than PSO-SVM and BP neural network.

Research highlights

? Fault diagnosis model of sensor by chaos particle swarm optimization algorithm and support vector machine is established. ? CPSO-SVM has higher diagnostic accuracy than PSO-SVM and BP neural network in fault diagnosis of wireless sensor. ? Chaos particle swarm optimization algorithm is employed to select the parameters of support vector machine.

2013

1.854

0.0

2012

1.854

0.0

. 2012, 39(11):null-null

On-line adaptive clustering for process monitoring and fault detection

2007

0.0

0.701

. 2007, 37(1):206-211

Neurofuzzy compensation control for reconfigurable manipulator

<FONT face=Verdana>College of Communication Engineering,Jilin University,Changchun 130022,China</FONT>

There are many uncertainties in real dynamic system of reconfigurable manipulator that make PID type or traditional control methods unable to realize accurate position control.Thus a neurofuzzy control scheme based on PD control of accurate model was developed to identify and compensate structured and unstructured uncertainties for reconfigurable manipulator.This neurofuzzy compensator infusing fuzzy and neural networks proved to be an effective compensation control strategy for the manipulator trajectory tracking.The dynamics was derived through geometric form NewtonEuler algorithm,and it is characterized by less computation complexity and universal on nlink dynamics equations than other modeling methods for reconfigurable manipulator system. A controller for a Revolute-Revolute-Prismatic(RRP) reconfigurable manipulator was designed and its effectiveness on tracking performance is validated by simulations.

由于可重构机械臂的动力学系统中存在大量的不确定性，导致PID等传统的控制器无法实现
精确的位置控制。作者在基于精确模型PD控制的基础上，提出了模糊神经控制算法辨识补偿结
构、非结构不确定性。通过模糊神经控制器融合了模糊逻辑和神经网络的各自优势，实现了
可重构机械臂轨迹跟踪的有效的补偿控制。基于牛顿欧拉的几何方法，推导了n连杆
可重构机械臂的动力学方程，该方法相对于其他形式的动力学方程，计算量小、通用性强。
最后以RRP (Revolute-Revolute-Prismatic) 三连杆机械臂为例研究设计了可重构机械臂
的控制器，并且通过仿真验证了算法对轨迹跟踪的有效性。

... 1 问题描述可重构机械臂子系统动力学模型可描述为^[11]: ...

2010

1.9

0.0

... 假设3 关联项h_i(q, q·, q··)有界且满足^[12]: ...