永磁同步电机调速系统的分数阶积分滑模控制

引用本文

黄家才, 施昕昕, 李宏胜, 徐庆宏, 石要武. 永磁同步电机调速系统的分数阶积分滑模控制. 44(6): 1736-1742
HUANG Jia-cai, SHI Xin-xin, LI Hong-sheng, XU Qing-hong, SHI Yao-wu. Speed control of PMSM using fractural order integral sliding mode controller. Journal of Jilin University Engineering and Technology Edition, 44(6): 1736-1742 复制到剪切板

Permissions

永磁同步电机调速系统的分数阶积分滑模控制

黄家才¹, 施昕昕¹, 李宏胜¹, 徐庆宏¹, 石要武²

1.南京工程学院自动化学院,南京 211167

2.吉林大学通信工程学院,长春 130022

作者简介:黄家才(1977-),男,副教授,博士.研究方向:运动控制,分数阶控制.E-mail:huangjiacai@126.com

基金:国家自然科学基金项目(61104085); 江苏省自然科学基金项目(BK20130744); 江苏省教育厅自然科学基金项目(13KJB510011); 江苏政府留学奖学金资助项目(JS-2012-051);

摘要

为了提高永磁同步电机(PMSM)调速系统对负载扰动及参数变化的鲁棒性,采用速度误差的分数阶微积分,设计了非线性积分滑模面,并提出一种基于分数阶积分滑模控制算法(FOISMC)的PMSM速度控制系统。通过Lyapunov定理证明了所设计的控制器的稳定性,并对该控制器进行了性能分析。理论分析和数值仿真结果表明:所提方法比整数阶积分滑模控制以及常规PI控制具有更好的动态性能和抗扰动能力,以及更高的速度跟随精度。

关键词: 自动控制技术; 永磁同步电机; 分数阶微积分; 积分滑模控制; 速度控制

中图分类号:TP271.4 文献标志码:A 文章编号:1671-5497(2014)06-1736-07

Speed control of PMSM using fractural order integral sliding mode controller

HUANG Jia-cai¹, SHI Xin-xin¹, LI Hong-sheng¹, XU Qing-hong¹, SHI Yao-wu²

1.School of Automation, Nanjing Institute of Technology, Nanjing 211167, China

2.College of Communication Engineering, Jilin University, Changchun 130022, China

Abstract

In order to improve the robustness of load disturbance and parameter uncertainties of the Permanent Magnet Synchronous Motor (PMSM) speed control system, first, a nonlinear integral sliding surface was designed based on the fractural order calculus of the speed error. Then, a robust Fractional Order Integral Sliding Mode Control (FOISMC) algorithm was proposed for the PMSM speed control system. The stability of the proposed FOISMC method was proved by the Lyapunov stability theory, and the performance of the proposed controller was analyzed. Analysis and numerical simulation results show that the proposed method has better dynamic performance, robustness and speed tracking accuracy than the conventional integer order Integral Sliding Mode Control (ISMC) method and PI control method.

Keyword: automatic control technology; permanent magnet synchronous motor; fractional calculus; integral sliding mode control; speed control

Show Figures

0 引言

永磁同步电机(Permanent magnet synchron-ous motor,PMSM)是一个典型的非线性、多变量耦合系统,其性能受到外部负载扰动、内部参数变化、对象未建模和非线性动态特性等不确定性的影响^{[ 1]}。为了获得良好的动态响应,一些鲁棒控制策略如非线性控制^{[ 2]}、自适应控制^{[ 3]}、 H_∞控制^{[ 4]}和滑模控制(SMC)^{[ 5]}等被相继引入到交流伺服系统的研究中。其中SMC以其鲁棒性强、响应快速、物理实现简单等优点而得到研究人员的重视,并被应用到交流伺服系统的控制中。为了解决传统滑模控制中存在的稳态误差问题,Chern等^{[ 6]}首先在滑模面的设计中引入积分项,Bailk等^{[ 7]}将这种积分滑模面应用到永磁同步电机控制器的设计中。滑模面中加入积分项,不仅可以减小系统稳态误差,有效削弱抖振,还可以增强控制器的稳定性^{[ 8]}。在上述研究中积分滑模面的设计通常是基于状态变量的整数阶积分,在大的初始误差或执行器饱和时,存在积分饱和效应,导致暂态性能下降甚至系统的不稳定。

分数阶微积分几乎与整数阶微积分有着同样悠久的历史,但长期以来分数阶微积分被认为是一个纯理论研究课题。近几十年来分数阶控制器的应用研究越来越吸引人们的注意,这主要是由于分数阶控制器能提供更多的自由度^{[ 9, 10, 11, 12, 13, 14, 15, 16]}。本文为了进一步提高PMSM调速系统的抗负载扰动能力以及对参数变化的鲁棒性、克服整数阶积分滑模面设计中存在的积分饱和效应等问题,将分数阶微积分理论应用到滑模面的设计中,提出了一种基于分数阶积分滑模面的PMSM速度控制算法,并进行了数值仿真以及对比试验。

1 分数阶微积分定义

分数阶微积分可以看作是整数阶微积分运算向非整数阶微积分运算的推广。用符号 $\begin{matrix} _{t_{0}} \end{matrix} \begin{matrix} D_{t}^{λ} \end{matrix}$ 表示分数阶微积分算子,定义如下^{[ 12]}:

$\begin{matrix} _{t_{0}} D_{t}^{λ} ≜ D^{λ} = \{\begin{matrix} \frac{d^{λ}}{d t^{λ}}, R (λ) > 0 \\ 1, R (λ) = 0 \\ \int_{t_{0}}^{t} {(dτ)}^{- λ}, R (λ) < 0 \end{matrix} (1) \end{matrix}$

式中:下标 t₀和 t分别表示算子定义中的下限和上限; λ为算子的阶次, R( λ)为 λ的实部,一般来说 λ∈ R,实际上 λ可以是任意复数。

分数阶微积分理论的发展过程中,出现很多种分数阶微积分定义,其中最常用的是Grunwald-Letnikov(GL)分数阶微积分定义^{[ 13]}、Riemann-Liouville(RL)分数阶微积分定义以及Caputo分数阶微积分定义^{[ 14]}。

(1)GL分数阶微积分定义如下:

$\begin{matrix} _{t_{0}} D_{t}^{λ} f (t) = \lim_{h \to 0} h^{- λ} \overset{[\frac{t - t_{0}}{h}]}{\sum_{j = 0}} {(- 1)}^{j} (\begin{matrix} λ \\ j \end{matrix}) f (t - jh) (2) \end{matrix}$

式中: λ为任意阶;[·]表示取整运算; h为计算步长; $\begin{matrix} (\begin{matrix} λ \\ j \end{matrix}) \end{matrix}$ = $\begin{matrix} \frac{λ!}{j! (λ - j)!} \end{matrix}$ 为二项式系数。

(2)RL分数阶微积分定义如下:

$\begin{matrix} _{t_{0}} D_{t}^{λ} f (t) = \frac{1}{Γ (n - λ)} \frac{d^{n}}{d t^{n}} \int_{t_{0}}^{t} \frac{f (τ)}{{(t - τ)}^{λ - n + 1}} d τ (3) \end{matrix}$

式中: n为整数,且 n-1 <λ<n; Γ(·)为伽马函数,且有 Γ( x) = $\begin{matrix} \int_{0_{}}^{{+∞}_{}} \end{matrix}$ e^-tt^x-¹d t。

(3)Caputo分数阶微积分定义如下:

$\begin{matrix} _{t_{0}} D_{t}^{λ} f (t) = \frac{1}{Γ (n - λ)} \int_{t_{0}}^{t} \frac{f^{n} (τ)}{{(t - τ)}^{λ - n + 1}} dτ (4) \end{matrix}$

式中: n为整数,且 n-1 <λ<n。

当 f( t)连续可导时,上述定义在工程应用中是等价的。零初始条件下,RL分数阶微积分定义下的拉普拉斯变换为:

$\begin{matrix} L {_{t_{0}} D_{t}^{λ} f (t)} = s^{λ} F (s) (5) \end{matrix}$

式中: F( s)为 f( t)的拉普拉斯变换。

显然,分数阶微积分算子与整数阶微积分算子相比具有更多的自由度。通过选择合适的分数阶次 λ,可以获得更好的控制性能。此外,从上述定义可以看出,连续函数的分数阶微分具有记忆特征。

2 永磁同步电机(PMSM)数学模型

本文所研究的PMSM的转子为表贴式永磁结构,定子绕组为星形接法,三相交流供电。在建模、分析以及设计过程中常做如下假设:

(1)转子永磁磁场在气隙空间的分布以及定子电枢绕组中的感应电动势均为正弦波。

(2)磁路不饱和,磁滞和涡流损耗忽略不计。

基于上述假设,建立在 d-q坐标系下永磁同步电机数学模型,其定子电压方程为^{[ 17]}:

$\begin{matrix} \begin{matrix} u_{d} = R_{s} i_{d} - ω_{e} L_{q} i_{q} + L_{d} \frac{d i_{d}}{dt} (6) \\ u_{q} = R_{s} i_{q} + ω_{e} L_{d} i_{d} + ω_{e} ψ_{f} + L_{q} \frac{d i_{q}}{dt} (7) \end{matrix} \end{matrix}$

式中: u_d、 u_q分别为定子电压在 d、 q轴上的分量; i_d、 i_q分别为定子电流在 d、 q轴上的分量; L_d、 L_q分别为定子电感在 d、 q轴上的分量; R_s为定子电阻; ψ_f为永磁体与定子交链的磁链; ω_e为转子电角速度。

d-q坐标系下的电磁转矩方程为:

$\begin{matrix} T_{e} = \frac{3}{2} P [ψ_{f} i_{q} + (L_{d} - L_{q}) i_{d} i_{q}] (8) \end{matrix}$

式中: T_e为电磁转矩; P为电机的极对数。

对于表贴式PMSM有 L_d=L_q,所以电磁转矩方程(8)可以写为:

$\begin{matrix} T_{e} = \frac{3}{2} P ψ_{f} i_{q} (9) \end{matrix}$

机械运动方程为:

$\begin{matrix} T_{e} - T_{L} = J \frac{d ω_{m}}{dt} + B ω_{m} (10) \end{matrix}$

式中: T_L为负载转矩; J为转动惯量; ω_m为转子机械角速度,且 ω_e =Pω_m; B为阻尼系数。

由式(9)(10)可得永磁同步电机的机械运动方程:

$\begin{matrix} {\overset{\cdot}{ω}}_{m} + a ω_{m} + d = b i_{q} (11) \end{matrix}$

式中: a= $\begin{matrix} \frac{B}{J} \end{matrix}$ , b= $\begin{matrix} \frac{3 P ψ_{f}}{2 J} \end{matrix}$ , d= $\begin{matrix} \frac{T_{L}}{J} \end{matrix}$ 。

考虑到电机运行过程中的参数不确定量,永磁同步电机的机械运动方程可以进一步写为:

$\begin{matrix} {\overset{\cdot}{ω}}_{m} + (a + Δa) ω_{m} + (d + Δd) = (b + Δb) i_{q} (12) \end{matrix}$

式中: Δa、 Δd、 Δb分别为参数 a、 d、 b的变化量。

PMSM速度控制系统中,控制器的设计目标是控制速度输出 ω_m严格跟随其参考输入信号 ω_ref。定义PMSM系统速度跟踪误差为:

$\begin{matrix} e (t) = ω_{ref} - ω_{m} (13) \end{matrix}$

式中: ω_ref为给定速度。

对速度误差 e( t)求导可得:

$\begin{matrix} \begin{matrix} \overset{\cdot}{e} (t) = {\overset{\cdot}{ω}}_{ref} - {\overset{\cdot}{ω}}_{m} = \\ {\overset{\cdot}{ω}}_{ref} + a ω_{m} + d - b i_{q} + Δa ω_{m} + Δd - Δb i_{q} = \\ {\overset{\cdot}{ω}}_{ref} - a (ω_{ref} - ω_{m}) + a ω_{ref} + d - b i_{q} + Δa ω_{m} + \\ Δd - Δb i_{q} = - ae (t) + φ (t) + δ (t) (14) \\ 式中 : φ (t) = {\overset{\cdot}{ω}}_{ref} + a ω_{ref} - b i_{q} (15) \\ δ (t) = Δa ω_{m} + Δd + d - Δb i_{q} (16) \end{matrix} \end{matrix}$

δ( t)为系统总的扰动量和不确定量。因为 Δa、 Δd、 d、 -Δb的变化是有界的,所以 δ( t)也是有界的。

3 分数阶积分滑模控制器设计

文献[7-8,18]中针对PMSM的速度控制,提出了如下积分滑模面:

$\begin{matrix} S = e (t) + c_{1} \int_{0}^{t} e (τ) dτ (17) \end{matrix}$

式中: c₁∈ R⁺。

该积分滑模面中只含有速度误差和速度误差的积分项,省去了加速度项,因此控制器中不含有速度误差的二阶导数项,增强了控制器的稳定性,而且可以减少系统稳态误差。文献[18]把该积分滑模面应用到PMSM的低速控制场合,取得了很好的控制效果。

式(17)所定义的积分滑模面中,速度误差的积分项为一阶整数积分,是一种全局积分,在大的初始误差或执行器饱和时,会产生积分饱和效应,导致暂态性能恶化甚至系统的不稳定^{[ 19]}。为了解决这一问题,下面设计一种基于分数阶积分滑模面的PMSM速度控制算法。

3.1 分数阶积分滑模面设计

定义如下分数阶积分滑模面:

$\begin{matrix} S = e (t) + c_{1} \times_{0} {D_{t}}^{- u} e (t) = e (t) + c_{1} D^{- u} e (t) (18) \end{matrix}$

式中: D^-ue( t)表示对误差 e( t)的分数阶积分,用于消除系统的稳态误差;0 <u<1为分数阶积分滑模面的阶次。

从式(18)可以看出,所提分数阶积分滑模面比传统整数阶积分滑模面多了一个自由度 u,通过选择合适的阶次 u可获得更好的动态性能。

为了进一步提高系统的鲁棒性,在分数阶积分滑模面(式(18))的基础上,设计如下分数阶全程积分滑模面^{[ 20, 21, 22]}:

$\begin{matrix} \begin{matrix} S = e (t) + c_{1} \times_{0} {D_{t}}^{- u} e (t) + ϕ (t) = \\ e (t) + c_{1} D^{- u} e (t) + ϕ (t) (19) \end{matrix} \end{matrix}$

式中: ϕ( t) =ϕ(0) e^-t/M, M为常数,且 M>0, M决定了 ϕ( t)的收敛速度; ϕ(0) =-e(0) -c₁ ×₀ $\begin{matrix} {D_{0}}^{- u} \end{matrix}$ e( t),其中 e(0)和₀ D $\begin{matrix} {_{0}}^{- u} \end{matrix}$ e( t)分别为误差 e( t)在 t=0时的初始值和分数阶积分值。可以看出,对任意的初始状态 e(0),在 t=0时刻有 S=0,即系统的初始状态就处在滑模面上,消除了到达过程。

3.2 分数阶积分滑模控制器(FOISMC)设计

对式(19)中的 S求导数可得:

$\begin{matrix} \overset{\cdot}{S} = \overset{\cdot}{e} (t) + c_{1} D^{1 - u} e (t) + \overset{\cdot}{ϕ} (t) (20) \end{matrix}$

当系统在滑模面上运动时有 $\begin{matrix} \overset{\cdot}{S} \end{matrix}$ =0,根据式(14)有:

$\begin{matrix} \begin{matrix} \overset{\cdot}{S} = - ae (t) + φ (t) + δ (t) + \\ c_{1} D^{1 - u} e (t) + \overset{\cdot}{ϕ} (t) = 0 (21) \\ 可求得 : \\ φ (t) = ae (t) - δ (t) - c_{1} D^{1 - u} e (t) - \overset{\cdot}{ϕ} (t) (22) \end{matrix} \end{matrix}$

采用等速趋近率,设计分数阶积分滑模控制律如下:

$\begin{matrix} φ (t) = ae (t) - c_{1} D^{1 - u} e (t) - \overset{\cdot}{ϕ} (t) - εsgn (S) (23) \end{matrix}$

式中: ε表示系统运动点趋近切换面 S=0的速率,且 ε>0;sgn( S)为符号函数。

根据式(15)(23),可获得 q轴电流控制量输出为:

$\begin{matrix} \begin{matrix} i_{q} = \frac{1}{b} ({\overset{\cdot}{ω}}_{ref} + a ω_{ref} - ae (t) + c_{1} D^{1 - u} e (t) + \\ \overset{\cdot}{ϕ} (t) + εsgn (S)) (24) \end{matrix} \end{matrix}$

3.3 分数阶积分滑模控制器的稳定性分析

为了证明所设计的分数阶积分滑模控制器的稳定性以及确定滑模增益 ε应满足的条件,定义如下Lyapunov函数:

$\begin{matrix} V = \frac{1}{2} S^{2} (25) \end{matrix}$

根据Lyapunov稳定性理论可知,当条件 $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ = $\begin{matrix} \overset{\cdot}{SS} \end{matrix}$ <0成立时,即满足滑模到达条件。对式(25)两边求导数,可得:

$\begin{matrix} \begin{matrix} \overset{\cdot}{V} = S \overset{\cdot}{S} = S [\overset{\cdot}{e} (t) + c_{1} D^{1 - u} e (t) + \overset{\cdot}{ϕ} (t)] = \\ S [- ae (t) + ϕ (t) + δ (t) + c_{1} D^{1 - u} e (t) + \overset{\cdot}{ϕ} (t)] = \\ S [- ae (t) + {\overset{\cdot}{ω}}_{ref} + a ω_{ref} - b i_{q} + \\ δ (t) + c_{1} D^{1 - u} e (t) + \overset{\cdot}{ϕ} (t)] = \\ S [δ (t) - εsgn (S)] = - ε |S| + δ (t) S \leq \\ - ε |S| + |δ (t)| |S| \leq \\ (|δ (t)| - ε) |S| (26) \end{matrix} \end{matrix}$

从式(26)可以看出:如果滑模增益满足 ε> $\begin{matrix} |δ (t)| \end{matrix}$ ,则 $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ <0,所设计的分数阶积分滑模控制器是稳定的,系统能从任意初始状态在有限时间内达到切换面。

当系统进入滑动模态区后,就开始滑模运动,因此必须保证系统在分数阶积分滑模面上的运动是渐进稳定的。当系统进入滑模态时,系统状态满足 S=0,即:

$\begin{matrix} e (t) + c_{1} D^{- u} e (t) + ϕ (t) = 0 (27) \end{matrix}$

由式(27)可得:

$\begin{matrix} D^{u} e (t) = - c_{1} e (t) - D^{u} ϕ (t) (28) \end{matrix}$

根据分数阶系统稳定性理论^{[ 21]},当 c₁ >0时有:

$\begin{matrix} |\arg (- c_{1})| > \frac{uπ}{2}, 0 < u < 1 (29) \end{matrix}$

此时分数阶微分方程(28)是渐进稳定的,即所设计的分数阶积分滑模面是存在的,且分数阶积分滑模控制系统能渐进稳定地收敛到零点。

为了削弱滑模控制存在的高频抖振现象,选择饱和函数sat( S/ξ)取代式(24)中的开关函数sgn( S),如式(30)所示:

$\begin{matrix} sat (S / ξ) = \{\begin{matrix} sgn (\frac{S}{ξ}), & |\frac{S}{ξ}| > 1 \\ \frac{S}{ξ}, & |\frac{S}{ξ}| \leq 1 \end{matrix} (30) \end{matrix}$

式中: ξ为饱和函数的边界层的宽度。

可以证明当采用饱和函数时,同样满足滑模控制器的稳定性条件。

3.4 分数阶积分滑模控制器的鲁棒性分析

参考式(17),采用全程积分滑模面,则可得到传统积分滑模控制器的输出为:

$\begin{matrix} \begin{matrix} i_{q} = \frac{1}{b} ({\overset{\cdot}{ω}}_{ref} + a ω_{ref} - ae (t) + \\ c_{1} e (t) + \overset{\cdot}{ϕ} (t) + εsgn (S)) (31) \end{matrix} \end{matrix}$

将式(31)与所提分数阶积分滑模控制器的输出式(24)做比较,可以得出如下结论:

(1)传统积分滑模面(17)中的积分项是一阶整数积分,也是一种全局积分,在整个时间范围内对误差 e( t)的积分权重是相同的,在大的初始误差条件下,会导致暂态性能恶化,尤其是执行器饱和时,会产生积分饱和效应,甚至导致系统的不稳定^{[ 19]}。而从式(18)可以看出:本文所设计的滑模面,对误差 e( t)的积分是分数阶积分,其积分权重在时间轴上的分布与阶次 u有关,并随时间变化而变化,具有对新的误差累积加以储存,对过去的误差累积则逐渐遗弃的特性。因此通过选择合适的阶次 u,可以有效地抑制积分饱和现象,提高系统的暂态性能。

(2)由于分数阶积分滑模面的阶次取值范围为 u∈(0,1),所以分数阶积分滑模控制器输出(见式(24))中的 D¹ ^-ue( t)项表示对误差 e( t)的分数阶微分,即对 e( t)的变化趋势敏感。因此当出现由于负载扰动导致速度输出偏离给定值时,式(24)因分数阶微分项 D¹ ^-ue( t)的存在能及时输出一个较大的电流控制值 i_q。该电流控制值 i_q可以及时有效地抑制电机速度的陡降,因此具有很好的鲁棒性。而传统积分滑模控制器的输出(见式(31))中,仅含有误差 e( t)的比例项,在负载扰动发生时无法及时抑制电机速度的陡降。

(3)分数阶积分滑模面的阶次 u取值越小,分数阶微分项 D¹ ^-ue( t)的输出越大,即微分作用加剧,会导致系统动态性能下降。特别地,当 u=0时,则分数阶微分项 D¹ ^-ue( t) =d e( t) /d t蜕变为一阶整数微分,此时式(24)含有误差 e( t)的比例微分(PD)项,可能导致系统振荡。所以在设计分数阶积分滑模面时,要结合参数 c₁的值选择合适的阶次 u。

4 仿真

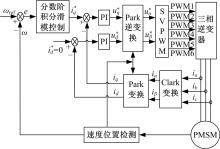
为了验证所设计的PMSM分数阶积分滑模控制算法的有效性,在Matlab环境下进行了仿真研究,并与传统的基于整数阶积分滑模面的积分滑模控制^{[ 7, 8, 18, 20]}、传统PI控制做了性能比较。所采用的电机参数为:额定转速2400 r/min; P=4; R_s =2 .46 Ω; L_d=L_q=4 .233 mH; J=1 .02 ×10 ^-³ kg·m²; B=1 .0 ×10 ^-⁴ N·m·s·rad ^-¹; ψ_f =0 .175 Wb。控制系统的总体框图如图1所示。

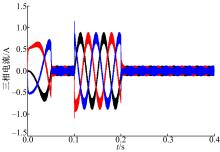
(1)负载扰动情况下,本文方法与传统积分滑模控制方法、PI控制方法的动态性能比较。电机空载起动,给定转子速度为斜坡输入,上升时间为0.05 s,稳态值为300 r/min,负载转矩在0.1 s时加载0.9 N·m,在0.2 s时变为0 N·m,分数阶积分滑模面的阶次为 u=0 .9。图2为3种方法控制下PMSM的速度动态输出比较图。从图中可以看出:当突加负载时,本文所提出的分数阶积分滑模控制方法控制的速度有更小的转速降落,而且能更快地调整到给定速度;当突卸负载时,也有相同的结论( 图2中只给出0.1 s突加负载时的速度输出局部放大图),这与第3.4节的结论(2)相符合。图3和图4分别为分数阶积分滑模控制器的 q轴控制电流输出以及PMSM的三相电流输出。可知, q轴控制电流输出较平滑,有效地抑制了抖动。

(2)负载扰动情况下,验证本文方法对正弦速度给定的跟踪能力,并与传统积分滑模控制方法作比较。

	Figure Option View Download New Window
	图1 永磁同步电机调速系统原理框图Fig.1 Block diagram of the PMSM speed control system

	Figure Option View Download New Window
	图2 本文方法与传统积分滑模控制、PI控制的斜坡响应比较Fig.2 Slope response comparison under the proposed method,conventional ISMC method and PI control method

	Figure Option View Download New Window
	图3 分数阶积分滑模控制的 q轴控制电流输出Fig.3 Current control output of q-axis under FOISMC method

正弦速度给定的峰值为300 r/min,频率为4π rad/s,在0.1 s和0.5 s时突然加载0.9 N·m负载,在0.2 s和0.6 s时突然卸载0.9 N·m负载。分数阶积分滑模面的阶次 u=0 .9。图5给出了本文所提方法和传统积分滑模控制方法控制下的电机速度输出, 图6进一步给出两种控制方法下的速度跟踪误差。从图6可以看出:本文方法能够精确地跟踪速度给定,且具有更小的跟踪误差。

	Figure Option View Download New Window
	图4 分数阶积分滑模控制的PMSM三相电流输出Fig.4 Three-phase current outputs of PMSM under FOISMC method

	Figure Option View Download New Window
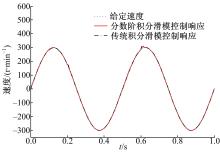	图5 本文方法与传统积分滑模控制的正弦响应比较Fig.5 Sine response comparison under the propose method and conventional ISMC method

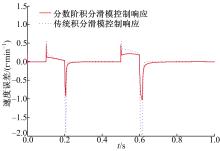	Figure Option View Download New Window
	图6 本文方法与传统积分滑模控制的正弦跟踪误差比较Fig.6 Sine track error comparison under the proposed method and conventional ISMC method

(3)分数阶积分滑模面的阶次 u取不同数值时,本文方法与传统积分滑模控制方法的性能比较。电机空载起动,给定转子速度为斜坡输入,上升时间为0.05 s,稳态值为1000 r/min。负载扰动为瞬时脉冲形式,频率为10 Hz,占空比为10%,幅度为0.9 N·m。电机运行2 s,当分数阶积分滑模面的阶次 u在区间 $\begin{matrix} [0.8,1) \end{matrix}$ 取不同数值时,其速度平方误差如表1所示。表1中平方误差定义如下:

$\begin{matrix} Δe = \int {(ω_{ref} (t) - ω_{m} (t))}^{2} dt (32) \end{matrix}$

表1 不同阶次下本文方法的速度平方误差 Table 1 Speed error square of the proposed method under different μ

从表1可以看出:当分数阶积分滑模面的阶次 u取值过小或过大时,本文方法的速度跟随误差较大;但是当阶次 u取适当数值时,本文方法比传统积分滑模控制方法Δ e=6.268具有更小的速度跟随误差,跟踪精度更高,这与第3.4节的结论(3)相符合。

5 结束语

本文设计的分数阶积分滑模面的阶次 u可调,通过选取适当的阶次 u可以获得最佳的控制性能。传统积分滑模控制算法可以看成本文方法的特例。该方法克服了传统积分滑模控制中由于大的初始误差或执行器饱和所导致的积分饱和效应以及暂态性能下降,具有比传统积分滑模控制以及常规PI控制更精确的速度跟随精度,以及更好的动态性能和抗扰动能力。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Slemon G R. Electrical machines for variable-frequency drives[J]. Proceeding of IEEE, 1994, 82(8): 1123-1139. [本文引用:1] [JCR: 6.911]
[2]	Rachid E, Mohand O. Nonlinear predictive controller for a permanent magnet synchronous motor drive[J]. Mathematics and Computers in Simulation, 2010, 81(2): 394-406. [本文引用:1] [JCR: 0.836]
[3]	Zhou J, Wang Y. Real-time nonlinear adaptive back stepping speed control for a PM synchronous motor[J]. Control Engineering Practice, 2005, 13(10): 1259-1269. [本文引用:1] [JCR: 1.669]
[4]	Hsien T L, Sun Y Y, Tsai M C. H_∞ control for a sensorless permanent magnet synchronous drive[J]. IEE Proceedings Electric Power Applications, 1997, 144(3): 173-181. [本文引用:1]
[5]	Mezouar A, Fellah M K, Hadjeri S. Adaptive sliding mode observer for induction motor using two-time-scale approach[J]. Electric Power Systems Research, 2007, 77(5): 604-618. [本文引用:1] [JCR: 1.694]
[6]	Chern T L, Wu Y C. Design of integral variable structure controller and application to electro hydraulic velocity servo systems[J]. IEE Proceedings D. IET, 1991, 138(5): 439-444. [本文引用:1]
[7]	Bailk I C, Kim K H, Youn M J. Robust nonlinear speed control of PM synchronous motor using boundary layer integral sliding mode control technique[J]. IEEE Transactions on Control System Technology, 2000, 8(1): 47-54. [本文引用:1] [JCR: 2.0]
[8]	童克文, 张兴, 张昱, 等. 基于新型趋近率的永磁同步电机滑模变结构控制[J]. 中国电机工程学报, 2008, 28(21): 102-106. Dong Ke-wen, Zhang Xing, Zhang Yu, et al. Sliding mode variable structure control of a permanent magnet synchronous machine based on a novel reaching law[J]. Proceedings of the CSEE, 2008, 28(21): 102-106. [本文引用:1]
[9]	Podlubny I. Fractional-order systems and PIλDμ-controllers[J]. IEEE Transactions on Automatic Control, 1999, 44(1): 208-214. [本文引用:1] [JCR: 2.718]
[10]	Li H S, Luo Y, Chen Y Q. A Fractional order proportional and derivative (FOPD) motion controller: tuning rule and experiments[J]. IEEE Transactions on Control Systems Technology, 2010, 18(2): 516-520. [本文引用:1] [JCR: 2.0]
[11]	Li Y, Chen Y Q, Podlubny I. Stability of fractional order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability[J]. Computers Mathematics with Applications, 2010, 59(5): 1810-1821. [本文引用:1]
[12]	Chen Y Q, Petras I, Xue D Y. Fractional order control-A tutorial[C]∥American Control Conference, 2009: 1397-1411. [本文引用:1]
[13]	Oldham K B, Spanier J. The Fractional Calculus[M]. New York: Academic Press, 1974. [本文引用:1]
[14]	Podlubny I. Fractional Differential Equations[M]. San Diego: Academic Press, 1999. [本文引用:1]
[15]	张碧陶, 皮佑国. 永磁同步电机伺服系统模糊分数阶滑模控制[J]. 控制与决策, 2012, 27(12): 1776-1780. Zhang Bi-tao, Pi You-guo. Fractional order fuzzy sliding mode control for permanent magnet synchronous motor servo drive[J]. Control and Decision, 2012, 27(12): 1776-1780. [本文引用:1] [CJCR: 0.907]
[16]	Delavari H, Ghaderi R, Ranjbar A, et al. Fuzzy fractional order sliding mode controller for nonlinear systems[J]. Communications in Nonlinear Science and Numerical Simulation, 2010, 15(4): 963-978. [本文引用:1] [JCR: 2.773]
[17]	Lin F J. Real-time IP position controller design with torque feedforward control for PM synchronous motor[J]. IEEE Transactions on Industrial Electronics, 1997, 44(3): 398-407. [本文引用:1] [JCR: 5.165]
[18]	王礼鹏, 张化光, 刘秀翀. 低速PMSM无速度传感器调速系统积分滑模控制[J]. 电机与控制学报, 2012, 16(2): 20-24. Wang Li-peng, Zhang Hua-guang, Liu Xiu-chong. Sensorless of integral sliding mode controlled PMSM at low speeds[J]. Electric Machines and Control, 2012, 16(2): 20-24. [本文引用:1] [CJCR: 1.0607]
[19]	李鹏, 郑志强. 非线性积分滑模控制方法[J]. 控制理论与应用, 2011, 28(3): 421-426. Li Peng, Zheng Zhi-qiang. Sliding mode control approach with nonlinear integrator[J]. Control Theory & Applications, 2011, 28(3): 421-426. [本文引用:2]
[20]	陈振, 耿洁, 刘向东. 基于积分时变滑模控制的永磁同步电机调速系统[J]. 电工技术学报, 2011, 26(6): 56-61. Chen Zhen, Geng Jie, Liu Xiang-dong. An integral and exponential time-varying sliding mode control of permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2011, 26(6): 56-61. [本文引用:1] [CJCR: 1.161]
[21]	Ahmed E, EI-Sayed A M A, EI-Saka H A. Equilibrium points, stability and numerical solutions of fractional order predator-prey and rabies models[J]. Journal of Mathematical Analysis and Applications, 2007, 325(22): 542-553. [本文引用:1] [JCR: 1.05]
[22]	史宏宇, 冯勇, 张袅娜. 感应电动机全局高阶滑模观测器[J]. 吉林大学学报: 工学版, 2013, 43(3): 688-694. Shi Hong-yu, Feng Yong, Zhang Niao-na. Global high-order sliding mode observer for induction motor[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(3): 688-694. [本文引用:1] [CJCR: 0.701]

1994

6.911

0.0

... 0 引言永磁同步电机(Permanent magnet synchron-ous motor,PMSM)是一个典型的非线性、多变量耦合系统,其性能受到外部负载扰动、内部参数变化、对象未建模和非线性动态特性等不确定性的影响^[1] ...

2010

0.836

0.0

. 2010, 81(2):null-null

Nonlinear predictive controller for a permanent magnet synchronous motor drive

... 为了获得良好的动态响应,一些鲁棒控制策略如非线性控制^[2]、自适应控制^[3]、H_{∞ ...}

2005

1.669

0.0

. 2005, 13(10):1259-1269 DOI:10.1016/j.conengprac.2004.11.007

Real-time nonlinear adaptive back stepping speed control for a PM synchronous motor

Abstract

A real-time nonlinear adaptive speed control scheme based on backstepping control technique is proposed for a permanent magnet synchronous motor. In the controller design, the input–output feedback linearization is firstly used to compensate the nonlinearities in the nominal system. Then, adaptive backstepping control approach is adopted to derive the control scheme, which is robust to the parameter uncertainties and load torque disturbance. Simulation and real-time experimental results clearly show that the proposed control scheme can track the speed reference signal generated by a reference model successfully under parameter uncertainties and load torque disturbance without singularity and overparameterization.

... 为了获得良好的动态响应,一些鲁棒控制策略如非线性控制^[2]、自适应控制^[3]、H_{∞ ...}

1997

0.0

... 控制^[4]和滑模控制(SMC)^[5]等被相继引入到交流伺服系统的研究中 ...

2007

1.694

0.0

. 2007, 77(5):null-null

Adaptive sliding mode observer for induction motor using two-time-scale approach

... 控制^[4]和滑模控制(SMC)^[5]等被相继引入到交流伺服系统的研究中 ...

1991

0.0

... 为了解决传统滑模控制中存在的稳态误差问题,Chern等^[6]首先在滑模面的设计中引入积分项,Bailk等^[7]将这种积分滑模面应用到永磁同步电机控制器的设计中 ...

2000

2.0

0.0

2008

0.0

... 滑模面中加入积分项,不仅可以减小系统稳态误差,有效削弱抖振,还可以增强控制器的稳定性^[8] ...

1999

2.718

0.0

2010

2.0

0.0

2010

0.0

. 2010, 59(5):null-null

Stability of fractional order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability

2009

0.0

... 用符号 t0Dtλ表示分数阶微积分算子,定义如下^[12]: ...

1974

0.0

... 分数阶微积分理论的发展过程中,出现很多种分数阶微积分定义,其中最常用的是Grunwald-Letnikov(GL)分数阶微积分定义^[13]、Riemann-Liouville(RL)分数阶微积分定义以及Caputo分数阶微积分定义^[14] ...

1999

0.0

2012

0.0

0.907

. 2012, 27(12):1776-1780

Fractional order fuzzy sliding mode control for permanent magnet synchronous motor servo drive

A scheme of fractional order sliding mode controller based on fuzzy logic algorithm is proposed for dealing
with the chattering phenomenon existing in conventional integral order sliding mode controller. The fractional order sliding
mode surface covers the whole control domain so that the system is robust with disturbances all over the control domain.
In order to deal with the upper bound of uncertainties, fuzzy logic inference algorithm is used to obtain the gain of softswitching.
Simulations and experiments demonstrate that the proposed fractional order sliding mode controller not only
achieves favorable control performances, but also is robust with regard to external disturbances.

针对传统整数阶滑模控制系统中的抖震问题, 结合分数阶理论、模糊逻辑推理和滑模控制技术的优点, 提出
了模糊分数阶滑模控制策略. 将传统滑模控制器中的整数阶切换面推广到分数阶并设计了全控制域滑模面, 保证系
统在整个控制域都具有较强的鲁棒性. 采用模糊逻辑推理算法, 实现了开关切换增益的自整定. 仿真和实验验证了模
糊分数阶滑模控制系统不但能有效地削减抖震, 而且能保持滑模控制器对系统外部扰动的全局鲁棒性.

2010

2.773

0.0

. 2010, 15(4):963-978 DOI:10.1016/j.cnsns.2009.05.025

Fuzzy fractional order sliding mode controller for nonlinear systems

Abstract

In this paper, an intelligent robust fractional surface sliding mode control for a nonlinear system is studied. At first a sliding PD surface is designed and then, a fractional form of these networks PD^α, is proposed. Fast reaching velocity into the switching hyperplane in the hitting phase and little chattering phenomena in the sliding phase is desired. To reduce the chattering phenomenon in sliding mode control (SMC), a fuzzy logic controller is used to replace the discontinuity in the signum function at the reaching phase in the sliding mode control. For the problem of determining and optimizing the parameters of fuzzy sliding mode controller (FSMC), genetic algorithm (GA) is used. Finally, the performance and the significance of the controlled system two case studies (robot manipulator and coupled tanks) are investigated under variation in system parameters and also in presence of an external disturbance. The simulation results signify performance of genetic-based fuzzy fractional sliding mode controller.

1997

5.165

0.0

... 基于上述假设,建立在d-q坐标系下永磁同步电机数学模型,其定子电压方程为^[17]: ...

2012

0.0

1.0607

... 4 仿真为了验证所设计的PMSM分数阶积分滑模控制算法的有效性,在Matlab环境下进行了仿真研究,并与传统的基于整数阶积分滑模面的积分滑模控制^[7,8,18,20]、传统PI控制做了性能比较 ...

2011

0.0

. 2011, 28(3):421-426

Sliding mode control approach with nonlinear integrator

针对一类不确定非线性系统的滑模控制,提出了一类具有"小误差放大,大误差饱和"功能的光滑非线性饱和函数来改进传统的积分滑模控制,以形成非线性积分滑模控制.在保持传统积分滑模控制跟踪精度的同时获得更好的暂态性能.应用Lyapunov稳定性理论和LaSalle不变性原理证明了对最终常值干扰可以完全抑制.考虑控制受限时,所设计的饱和控制器类似于一种PD+非线性I控制器.最后,仿真算例验证了所提的非线性积分滑模控制方法的有效性.

... 式(17)所定义的积分滑模面中,速度误差的积分项为一阶整数积分,是一种全局积分,在大的初始误差或执行器饱和时,会产生积分饱和效应,导致暂态性能恶化甚至系统的不稳定^[19] ...

... (1)传统积分滑模面(17)中的积分项是一阶整数积分,也是一种全局积分,在整个时间范围内对误差e(t)的积分权重是相同的,在大的初始误差条件下,会导致暂态性能恶化,尤其是执行器饱和时,会产生积分饱和效应,甚至导致系统的不稳定^[19] ...

2011

0.0

1.161

. 2011, 26(6):56-61

An integral and exponential time-varying sliding mode control of permanent magnet synchronous motors

Beijing Institute of Technology Beijing 100081 China

In this paper the speed regulator based on sliding mode control strategies is used in the vector control of permanent magnet synchronous motor (PMSM) system. An integral and exponential time-varying sliding mode controller is proposed, which can avoid the problems of weak robustness and poor performance of dynamic response. The integral of speed error is introduced into sliding surface to avoid the requirements of the acceleration signal and enhance the system’s anti-jamming capability. Then the time-varying term is introduced to improve the convergence speed of the sliding surface in the context of ensuring global stability of the system. Experimental results obtained from PMSM control system experimental platform show that the integral time-varying sliding mode control achieves a precise speed control. Compared with PID traditional methods, the proposed sliding mode controller has better and faster tracking performance.

针对永磁同步电机(PMSM)矢量控制系统, 设计了一种积分时变滑模变结构的速度环控制器, 解决了传统PID控制器鲁棒性差、系统抗扰能力弱和动态响应性能不佳的问题。在滑模面的设计中引入误差信号的积分项, 避免控制量中对加速度信号的要求, 增强系统的抗干扰能力;同时引入时变项, 在保证系统全局稳定的前提下提高了滑模面的收敛速度。在基于DSP的PMSM实验平台上进行实验, 结果表明, 所提出的积分时变滑模控制方法能够实现精确的速度控制, 与传统的PID控制方法相比, 能够更好、更快地跟踪给定速度信号。

2007

1.05

0.0

. 2007, 325(22):null-null

Equilibrium points, stability and numerical solutions of fractional order predator-prey and rabies models

... 根据分数阶系统稳定性理论^[21],当c₁> ...

2013

0.0

0.701

. 2013, 43(3):688-694 DOI:10.7964/jdxbgxb201303022

Global high-order sliding mode observer for induction motor

1. College of Electrical Engineering & Automation, Harbin Institute of Technology, Harbin 150001, China;<br />2. Department of Automation, Changchun University of Technology, Changchun 130012, China;<br />3. College of Automotive Engineering, Jilin University, Changchun 130022, China

A global sliding mode observer for induction motor based on high-order sliding mode was proposed. The model is applied for precisely identifying the rotor velocity and the rotor flux of the induction motor. A global sliding mode surface was designed to improve the robustness of the observer and to implement the observer in the sliding motion through the entire response. A high-order sliding mode control law was utilized to obtain the smooth equivalent control signal directly. The control signal of the sliding mode observer can be applied to state observation, so that the better observing precision is realized. Simulation and experiment results show that the proposed sliding mode observer can eliminate the chattering phenomenon effectively, provide high observing precision. Moreover, the proposed observer is robust to load disturbance and internal parameter perturbation.

提出了一种基于高阶滑模的感应电动机全局滑模观测器,用于实现电机转速及转子磁链的高精度辨识.通过设计全局滑模面,实现了观测器在整个控制过程中均处于滑动模态,提高了观测器的鲁棒性.设计的高阶滑模控制律可以得到平滑的等效控制信号,实现了直接将滑模控制信号用于系统状态观测,提高了观测精度.仿真和试验结果表明:所设计的滑模观测器有效地抑制了抖振现象,具有良好的观测精度,并且对外部负载扰动及内部参数摄动具有较强的鲁棒性.