作者简介:李元春(1962-),男,教授,博士生导师.研究方向:智能机械与机器人控制.E-mail:liyc@mail.ccut.edu.cn
利用驱动Jacobian矩阵构建机械臂系统与液压伺服系统的耦合关系,进而建立整个系统的动力学模型。考虑系统未建模动态和外界干扰,通过定义虚拟控制量并选取合适的Lyapunov函数,设计此系统的自适应二阶滑模控制律,使系统在有限时间内精确跟踪期望轨迹且保持强鲁棒性,同时有效削弱了传统滑模控制对系统硬件不利的抖振。仿真结果验证了本文方法的有效性。
The coupling relationship between the manipulator and the hydraulic servo system is constructed by a driven Jacobian matrix. Then, the entire system dynamic model is established. Considering the unmodeled dynamic and external disturbance, the Adaptive Second Order Sliding Mode Control (ASOSMC), which can guarantee the tracking performance in finite time and strong robustness, is obtained by defining virtual control law and selecting suitable Lyapunov function. Simulation results show the effectiveness of the proposed control scheme, which can reduce the chattering phenomenon in traditional sliding mode which is harmful to hardware.
具有高耐用性、高功率/自重比、大作业范围等特点的液压机械臂, 已广泛应用于能源开采、建筑和交通运输等领域。目前, 针对液压机械臂系统的轨迹跟踪问题, 学者们提出了滑模控制、神经网络控制、自适应控制、鲁棒控制、模糊控制等方法。Le等[1]提出一种神经网络模糊控制方法, 实现了迷你液压机械臂的轨迹跟踪。Mohanty等[2]针对存在参数不确定性的液压机械臂系统的轨迹跟踪问题, 提出一种直接鲁棒自适应控制方法。Amer等[3]针对存在不确定性的机械臂系统, 提出一种新的自适应模糊滑模控制方法, 自适应地调整模糊系统的控制参数和滑模面斜率, 获得很好的轨迹跟踪效果, 并且明显抑制了抖振。Neila等[4]通过对机械臂系统不确定性和外界干扰的自适应估计, 提出一种鲁棒自适应终端滑模控制方法。Capisani等[5]在具有未知障碍的工作空间, 设计一种二阶滑模控制器对机械臂进行力/位置控制。Van等[6]提出一种基于二阶滑模观测器的输出反馈控制方法。Capisani等[7]利用一个MIMO辨识程序准确辨识机械臂动力学模型的相关参数, 进而设计基于逆动力学的二阶滑模控制器, 并且在SMART3-S2工业机器人上进行测试, 获得良好的跟踪性能。凌睿等[8]针对悬臂式掘进机器人提出基于有限状态结构的二阶滑模控制, 在无速度观测器的情况下, 实现精确轨迹跟踪, 削弱了传统滑模控制中的抖动问题, 提高了系统控制精度。吴玉香等[9]针对一种移动机械臂提出二阶滑模控制方法, 获得较好的轨迹跟踪效果, 并有效地削弱滑模控制系统的抖振。然而, 在实际工程中会面临各种不确定性因素, 对液压机械臂环境适应性、效率和精度的要求也在不断提高[10], 单纯地依靠某种智能控制方法已很难满足控制需要。
本文基于反演设计方法, 通过选取中间虚拟控制量, 逐步构造合适的Lyapunov函数, 直至完成液压机械臂轨迹跟踪的自适应二阶滑模控制器设计。该方法利用自适应律估计系统未知的总体不确定性[11], 使液压机械臂的关节角精确跟踪期望轨迹的同时保持强鲁棒性, 并且削弱传统滑模控制的“ 抖振” 现象[12]。根据Lyapunov稳定性理论证明了液压机械臂系统的渐近稳定性。
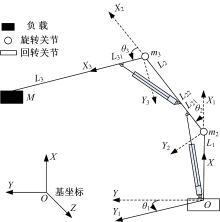
图1为本文所建的液压机械臂系统, 其中机械臂系统由三个刚性连杆、一个回转底座和两个旋转关节组成。 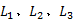
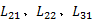
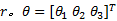
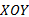
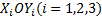
机械臂系统的总动能为:

式中: 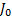
机械臂系统的总势能为:
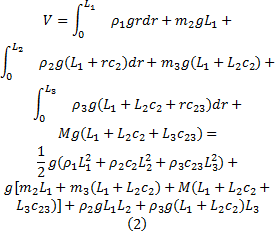
根据Lagrange原理可得机械臂系统动力学模型为:
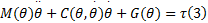
式中: 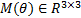
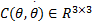


考虑未建模动态和外界干扰, 式(3)可改写为:
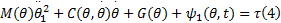
式中: 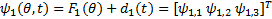
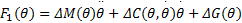
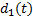
假设1 机械臂系统的总体不确定项是能量有界函数, 满足 
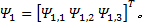
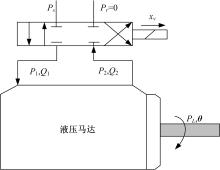
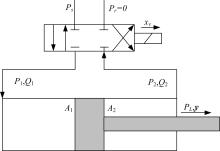
液压机械臂的液压伺服驱动系统由一个阀控液压马达(见图2)和两个阀控液压缸组成(见图3)。
假设相对于机械系统的时间常数, 液压伺服阀的时间常数可以忽略不计, 则伺服阀阀芯位移与控制输入成正比:
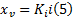
式中: 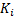
根据图1所示阀控单出杆液压缸的安装位置, 由余弦定理可得关节角与活塞位移的关系如下:
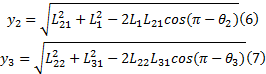
对式(6)和式(7)求导可得:

式中: 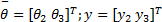

忽略外泄漏量, 根据式(5)、式(8)和液压伺服系统基本原理[13], 可得液压马达和液压缸的动态模型分别为:
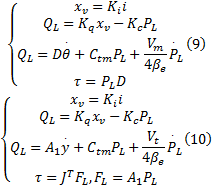
由式(9)和式(10)可求得三自由度液压驱动机械臂控制量与驱动力矩间的关系[14]为:
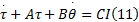
式中: 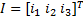
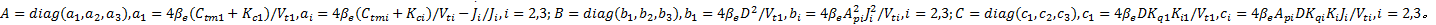
考虑未建模动态和外界干扰, 式(11)可写为:

式中: 
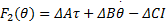
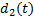
假设2 液压伺服系统的总体不确定项是能量有界信号, 
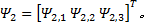
根据式(4)和式(12), 可得三自由度液压机械臂动力学方程为:
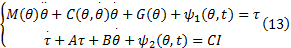
令 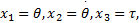
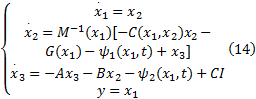
根据反演设计的思想, 自适应二阶滑模控制器的设计分为如下三步。
第一步:设 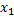
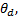
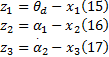
式中: 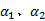
取滑模面:
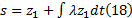
式中: 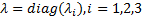
对式(15)求导得:
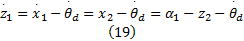
定义第一个虚拟控制量 
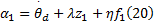
式中: 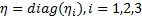
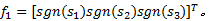
对式(18)求导得:

选取第一个Lyapunov函数为
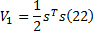
对上式求导得:
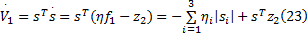
第二步:定义 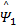
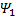

定义第二个虚拟控制量 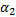
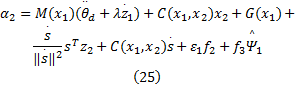
式中: 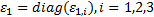
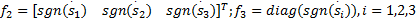
取自适应更新律为:
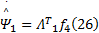
式中: 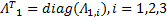
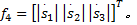
对式(18)求二阶导数得:
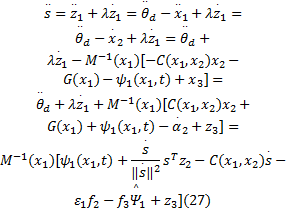
选取第二个Lyapunov函数为:
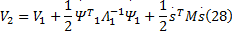
对上式求导可得:
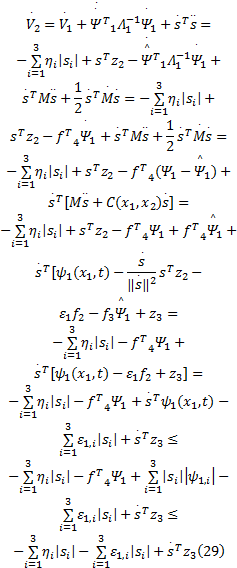
第三步:定义 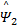
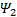
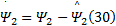
设计液压机械臂系统的实际控制律为:
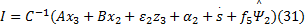
式中: 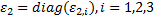

取自适应更新律为:
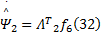
式中: 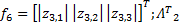
定理 针对液压机械臂系统动力学模型(13)与状态方程(14), 选取式(18)的滑模面, 设计如式(31)的自适应二阶滑模控制律, 则系统闭环一致渐近稳定。
证明 选取第三个Lyapunov函数为:

对上式求导可得:
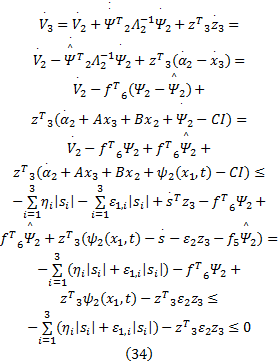
因此, 根据Lyapunov稳定性理论和Barbalat引理[15]可知, 当 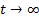
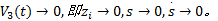
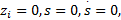
为了验证本文控制算法的有效性, 利用系统参数如表1和表2所示的液压机械臂进行仿真。
| 表1 机械臂系统参数 Table 1 Parameters of manipulator |
| 表2 液压伺服系统参数 Table 2 Parameters of hydraulic servo system |
未建模动态和外界干扰如下:
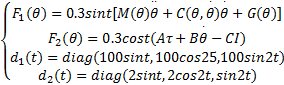
期望轨迹和初始值如下:
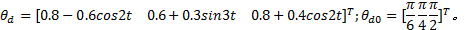
控制器参数如下:
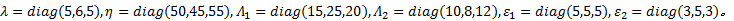
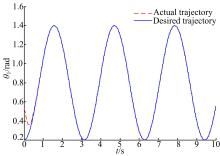
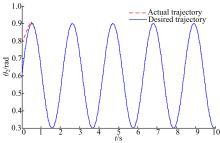
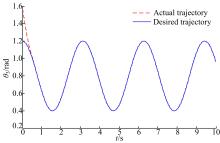
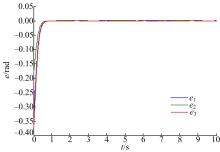
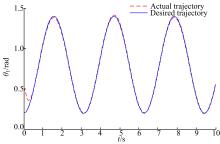
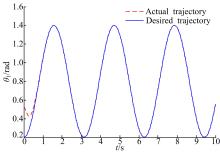
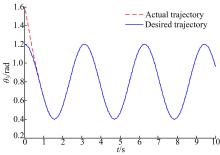
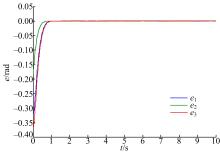
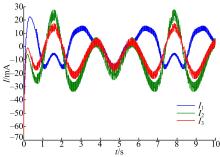
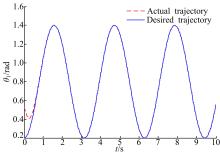
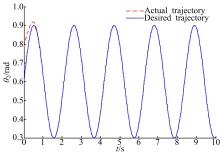
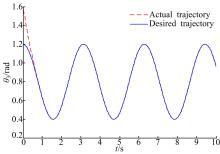
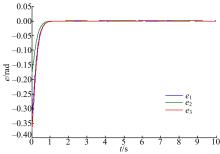
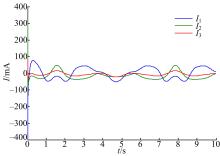
本文针对液压机械臂的轨迹跟踪问题, 分别采用自适应滑模控制(ASMC)、二阶滑模控制(SOSMC)及本文(ASOSMC)方法进行对比仿真, 仿真结果如图4~图13所示。
由图4~图7可以看出, 不考虑系统总体不确定性时二阶滑模控制可以得到比较好的跟踪性能, 而在考虑系统总体不确定时二阶滑模控制的跟踪性能变差, 跟踪误差较大。由图8~图13可以看出, 在考虑系统总体不确定性时, ASMC和ASOSMC都可以使各关节快速、精确地跟踪上期望轨迹, 并且使液压机械臂系统具有较强的鲁棒性, 但ASOSMC具有控制电流连续、抖振抑制效果好的优点。
液压机械臂系统具有多参数时变、含有总体不确定性、强耦合等特点。本文利用反演设计方法构造液压机械臂系统的Lyapunov函数, 进而设计出可保证整个系统渐近稳定的自适应二阶滑模控制律, 通过自适应算法在线补偿系统未建模动态及外部扰动, 使系统在精确轨迹跟踪的同时保持强鲁棒性, 并且有效削弱了传统滑模控制的抖振现象。
The authors have declared that no competing interests exist.
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|