基于无源理论的线控转向汽车稳定性控制

引用本文

何磊, 马伯祥, 郑宏宇, 王祥. 基于无源理论的线控转向汽车稳定性控制. 2015, 45(6): 1737-1742
HE Lei, MA Bo-xiang, ZHENG Hong-yu, WANG Xiang. Stability control of steering-by-wire vehicle based on passive theory. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1737-1742 复制到剪切板

Permissions

基于无源理论的线控转向汽车稳定性控制

何磊¹, 马伯祥², 郑宏宇¹, 王祥³

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.中国第一汽车股份有限公司技术中心,长春 130011

3.广州汽车集团股份有限公司汽车工程研究院,广州 511434

郑宏宇(1980-),男,副教授,博士.研究方向:汽车底盘控制.E-mail:zheng.hongyu@ascl.jlu.edu.cn

作者简介:何磊(1982-),男,讲师,博士.研究方向:汽车底盘控制.E-mail:jlu_helei@126.com

基金:国家自然科学基金项目(51505179,51505178,51575223)

摘要

为了解决线控转向系统受传感器精度及信号噪声等因素影响引起的系统控制失稳问题,利用无源理论,从能量角度分析系统,设计了无源控制器,保证了线控转向系统的控制稳定性。以机械转向系统的无源性分析为基础,对线控转向系统进行无源性分析。确定线控转向系统易呈现有源状态的部分,针对该部分设计无源控制器,保证其无源性,完成系统的稳定性控制,并通过实车试验对方法的有效性进行验证,结果表明:利用无源理论设计的无源控制器能够保证线控转向系统控制的稳定性。

关键词: 车辆工程; 线控转向; 稳定性控制; 无源控制器

中图分类号:U463.4 文献标志码:A 文章编号:1671-5497(2015)06-1737-06

Stability control of steering-by-wire vehicle based on passive theory

HE Lei¹, MA Bo-xiang², ZHENG Hong-yu¹, WANG Xiang³

1.State Key Laboratory of Automobile Simulation and Control, Jilin University, Changchun 130022, China

2.R&D Center, China FAW Co., Ltd, Changchun 130011, China

3.Automobile Engineering Institute, Guangzhou Automobile Group Co., Ltd, Guangzhou 511434, China

Abstract

A passive controller is developed to solve the problem of instability of steering-by-wire system caused by the inaccuracy of sensor and signal noise. The passive controller is designed with the analysis of the steering-by-wire system from the aspect of energy based on passive theory, thus ensuring the control stability of the system. The passivity of the steering-by-wire system is analyzed based on passivity analysis of mechanical steering system. The part of the steering-by-wire system that is easy to show the active state is confirmed, and the passive controller is designed to ensure its passivity, thus achieving the stability control of the system. The method is verified through real vehicle test. The results show that the passive controller designed based on passive theory can guarantee the control stability of the steering-by-wire system.

Keyword: vehicle engineering; steering-by-wire; stability control; passive controller

Show Figures

0 引言

线控转向系统(Steering-by-wire system, SBW)作为一种双向遥操作系统, 稳定性不仅是评价其双向控制结构的重要性能, 更是所有控制系统的共同要求^[1]。SBW双向控制结构中, 转向盘模块的控制输入和状态(或输出)分别是转向执行模块的状态(或输出)和控制输入, 反之亦然。如果分别考虑每个子模块的控制器设计问题, 即使各模块的子控制系统稳定, 也不能保证整合在一起的SBW双向控制系统稳定。对于任意一个模块的控制器设计而言, 它的被控对象除了本模块包含的物理元件, 还包含另一个模块的控制子系统。因此, 要使SBW双向控制结构稳定工作, 还需要应用一定的稳定性控制方法。

Raju^[2]首先提出使用二端口网络理论来分析力反馈遥操作机器人系统, 得出导致系统不稳定的原因是时延造成了通信环节的有源性。Xi等^[3]针对力反馈遥操作机器人的信号传输环节引起的不确定时延问题, 提出了基于事件的控制算法, 以保证随机时延对系统稳定性的影响。Chopra等^[4]通过频域优化技术, 提出了阻抗匹配滤波器设计, 保证遥操作系统的无源性和透明性。Li等^[5]提出了基于操作对象等效阻抗在线估计的自适应无源控制算法, 用于保证较大时延下力觉临场感机器人的稳定性。

本文利用无源理论, 从能量角度分析系统, 设计了无源控制器, 解决受实际系统传感器精度及信号噪声等因素影响引起的线控转向系统双向控制的失稳问题。线控转向系统使用转矩驱动/位置反馈式的双向控制结构, 在此结构的控制方法基础上叠加稳定性的控制方法, 先以机械转向系统的无源性分析为基础, 对线控转向系统进行无源性分析; 再确定线控转向系统易呈现有源状态部分, 针对该部分设计无源控制器, 保证其无源性, 完成系统的稳定性控制; 最后通过实车试验验证了该方法的正确性和有效性。

1 线控转向系统转矩驱动/位置反馈式双向控制结构

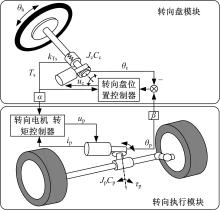
汽车线控转向系统通过控制两个或者更多的电机来控制转向盘和转向车轮, 达到对两个模块转角和转矩的耦合控制的目的^[6]。为了实现模块间转角与转矩的稳定耦合, 本文设计使用转矩驱动/位置反馈式SBW系统的双向控制结构, 如图1所示。

	Figure Option View Download New Window
	图1 线控转向系统双向控制结构示意图Fig.1 Bilateral control structure of SBW system

不同于通常的SBW系统控制结构, 该结构使用转向盘为“ 从” , 转向车轮为“ 主” 的控制思想^{[7, 8]}:转向盘模块采用位置闭环控制, 控制目标为小齿轮转角与SBW轴间角传动比之积, 状态反馈为转向柱的转角, 扰动输入为转向盘力矩; 转向执行模块采用转矩闭环控制, 控制目标为转向盘力矩与SBW力传动比之积, 状态反馈为转向电机的电枢电流。前者构成了转向盘模块与转向执行模块间的位置耦合关系; 后者构成了两模块间的转矩耦合关系。两者共同实现了SBW系统转向盘与转向车轮间位置和转矩的耦合关系。图中, α 为小齿轮轴驱动转矩与转向盘力矩的比值, 即线控转向系统力传动比; β 为转向柱至小齿轮轴转角的角传动比。θ _h、θ _c分别为转向盘和转向管柱总成转角; θ _p为小齿轮轴转角; τ _p为等效到小齿轮轴上的车轮与地面间转向阻力矩; k_Ts为扭矩传感器的刚度; T_s为扭矩传感器测量转矩; J_c为扭杆下部分等效到转向柱上的转动惯量; C_c为扭杆下部分等效到转向柱上的阻尼系数; J_p为转向执行模块等效到小齿轮轴上的转动惯量; C_p为该模块等效到小齿轮轴上的阻尼系数。u_c为力感模拟电机的电枢电压; u_p、i_p分别为转向电机的电枢电压、电枢电流。

驾驶员对于转向系统的输入可以从转角输入和转矩输入两个角度考虑:前者可用于多数开环和闭环行驶工况仿真; 后者可用于车辆转向后的回正行驶工况仿真。考虑到转矩输入模式仅适用于回正行驶工况, 且回正时输入为零, 利用转角输入模式对双向控制结构进行分析, 转角输入模式控制结构如图2所示。

	Figure Option View Download New Window
	图2 转角输入模式控制结构Fig.2 Control structure of angle input mode

图2中, T_c为力感模拟电机作用于转向柱的转矩; T_p为转向电机作用于小齿轮轴的转矩; 为了简化控制结构框图, G_Tp(s)为小齿轮驱动转矩闭环控制传递函数; G_Ts(s)为转向盘力矩对于转向柱转角的前馈控制环节; G_Tc(s)为力感模拟机构转矩闭环控制传递函数。SBW的双向控制的两个控制环节就是对传递函数G_Tp(s)、G_Tc(s)和G_Ts(s)的优化设计过程, 改变车辆转向性能的变传动比就是对力传动比α 及角传动比β 的设计过程。本文对这部分不进行深入的讨论, 重点研究在转矩驱动/位置反馈式SBW系统的双向控制结构下, 利用无源理论, 实现线控转向系统的稳定性控制方法。

2 无源性分析

2.1 机械转向系统的无源性分析

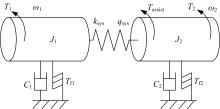
机械式汽车转向系统经简化后可表示为如图3所示的结构。

	Figure Option View Download New Window
	图3 简化的机械式转向系统Fig.3 Simplified mechanical steering system

图3中, J₁, C₁, T_f1分别为等效到转向盘处的转动惯量、阻尼和摩擦力矩; J₂, C₂, T_f2分别为等效到转向车轮处的转动惯量、阻尼和摩擦力矩; u=(T₁, T₂)为驾驶员的输入力矩和路面/车轮间的转向阻力矩组成的输入向量; y=(ω ₁, ω ₂)为J₁的转速和J₂的转速组成的输出向量; k_sys和q_sys分别为转向系统刚度和变形量。那么, 输入转向系统的能量可以表示为:

$\begin{matrix} \begin{matrix} \int_{0}^{t} u (s) y^{T} (s) ds = \\ \int_{0}^{t} T_{1} (s) ω_{1} (s) + T_{2} (s) ω_{2} (s)] ds = \\ \int_{0}^{t} J_{1} {\overset{\cdot}{ω}}_{1} (s) + C_{1} ω_{1} (s) + T_{f 1} sign (ω_{1} (s)) + \\ k_{sys} q_{sys} (s)] ω_{1} (s) + [J_{2} ω_{2} (s) + C_{2} ω_{2} (s) + \\ T_{f 2} sign (ω_{2} (s)) - k_{sys} q_{sys} (s)] ω_{2} (s)} ds = \\ [J_{1} ω_{1}^{2} (s) / 2 + J_{2} ω_{2}^{2} (s) / 2 + k_{sys} q_{sys}^{2} (s) / 2] |_{s = 0}^{s = t} + \\ [C_{1} \int_{0}^{t} ω_{1}^{2} (s) ds + C_{2} \int_{0}^{t} ω_{2}^{2} (s) ds + \\ T_{f 1} \int_{0}^{t} ω_{1} (s) | ds + T_{f 2} \int_{0}^{t} ω_{2} (s) | ds] = \\ E [x (t)] - E [x (0)] + dis (t) \geq 0 (1) \end{matrix} \end{matrix}$

式中: $\begin{matrix} \int_{0}^{^{t}} \end{matrix}$ u(s)y^T(s)ds为输入系统的能量; E[x(0)]为系统在t=0时刻的初始能量; E[x(t)]-E[x(0)]为系统在t时间内存储的能量; dis(t)为系统耗散的能量。

存在一个非负的状态函数E[x(t)]和非负函数dis(t), 使输入系统的能量非负, u→ y的映射是无源的^[9]。因此, 机械转向系统是一种二端口的网络系统^[10], 且对于驾驶员力矩输入和转向阻力矩输入来说, 是无源的。可以看到:由二端口输入到转向系统的能量, 一部分作为转向系统的动能和势能储存了起来, 另一部分则用于克服转动时的阻尼和摩擦以热能的方式耗散掉了。

2.2 动力转向系统的无源性分析

机械转向系统的无源性结论同样适用于其他具有助力的汽车转向系统。不同于机械转向系统的是:动力转向系统的输入向量变为u'=(T₁, T₂, T_assist), 相应的输出向量变为y'=(ω ₁, ω ₂, ω ₂), 图4为简化后的动力转向系统。

	Figure Option View Download New Window
	图4 简化的动力转向系统Fig.4 Simplified power steering system

由式(1)的推导过程可以证明:动力转向系统是一种具有3端口的网络系统, 且对于驾驶员力矩输入、助力矩输入和转向阻力矩输入来说, 是无源的。

2.3 线控转向系统的无源性分析

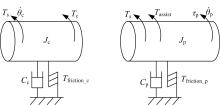
通过对机械和动力转向系统的无源性分析可知:转向系统中存在阻尼和摩擦, 系统的机械部件对于所有外部的功率输入一定是无源的。对采用转矩驱动/位置反馈式双向控制结构的SBW系统而言, 转向执行模块的控制方法与助力转向系统原理基本相同, 助力转矩T_assist可以分为两部分:一部分转矩是对驾驶员输入的放大, 即“ 助力特性” ; 另一部分转矩用于补偿部分转向系统的机械特性, 如转动惯量、阻尼和摩擦, 即补偿控制。结合前面的符号定义, 简化后的SBW系统如图5所示, 可将其看成5端口网络系统。

	Figure Option View Download New Window
	图5 简化的线控转向系统Fig.5 Simplified steering-by-wire system

图5中, T_assist为将SBW系统等效为动力转向系统后, 除去驾驶员输入力矩的助力部分; T_{friction_c}为转向盘模块等效在转向管柱上的摩擦力矩; T_{friction_p}为转向执行模块等效在小齿轮上的摩擦力矩。

根据机械和动力转向系统的无源性证明和分析结果, 当SBW系统在输入向量为u₁=(T_s, T_assist, τ _p)、输出向量为y₁=( $\begin{matrix} {\overset{\cdot}{θ}}_{c} \end{matrix}$ , $\begin{matrix} {\overset{\cdot}{θ}}_{p} \end{matrix}$ , $\begin{matrix} {\overset{\cdot}{θ}}_{p} \end{matrix}$ )时, 系统是无源的。那么对于输入向量u₂=(T_c, T_s)和输出向量y₂=( $\begin{matrix} {\overset{\cdot}{θ}}_{c} \end{matrix}$ , $\begin{matrix} {\overset{\cdot}{θ}}_{p} \end{matrix}$ ), 若能保证这两个端口的子控制系统是无源的, 就能保证整个SBW系统的无源性, 即SBW系统是稳定的。

3 线控转向系统的稳定性控制

当SBW系统作为一个整体工作时, 为了保证双向控制结构的运行稳定性, 只需要保证系统对于上述输入u₂和输出y₂是无源的即可。

由于控制系统的实时计算过程是离散的, 为了考查多端口网络系统的稳定性, 定义无源观测器如下:

式中:Δ t为无源观测器的采样周期。

多端口网络系统的转矩输入u=(T₁, …, T_m); 转速输出y=(ω ₁, …, ω _m), 多端口网络系统定义如图6所示。

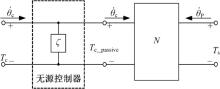
	Figure Option View Download New Window
	图6 多端口网络Fig.6 Multi-port network system

若对于每个采样时刻s, 有E_obs(s)≥ 0, 则表明系统在耗散能量; 若某一时刻出现E_obs(s)< 0, 则表明系统产生了-E_obs(s)能量。随着系统操作条件和端口动力学特性的变化, 无源观测器的值可能时正时负, 如果该值一直为负, 系统则是不稳定的。既然能够观测到系统产生的能量, 便可以设计一种时变的控制环节来耗散多余的能量, 保证系统的无源性, 也就保证了系统的稳定性。这个时变的控制环节就是无源控制器, 它可以设计在控制系统内部来消耗系统的能量, 以达到端口的无源要求。建立SBW系统输入u₂和输出y₂的二端口网络及无源控制器如图7所示。

	Figure Option View Download New Window
	图7 SBW系统的无源稳定性控制Fig.7 Passive stability control method of SBW system

设计无源控制器如下:

$\begin{matrix} \begin{matrix} E_{obs} (s) = E_{obs} (s - 1) + [T_{c} (s) θ_{c} (s) + \\ T_{s} (s) θ_{p} (s) + ξ (s - 1) θ_{c}^{2} (s - 1)] Δt (3) \\ ξ (s) = \{\begin{matrix} - \frac{E_{obs} (s)}{Δt {\overset{\cdot}{θ}}_{c}^{2} (s)}, E_{obs} (s) < 0 \\ 0, E_{obs} (s) \geq 0 \end{matrix} (4) \\ T_{c_passive} (s) = T_{c} (s) + ξ (s) θ_{c} (s) (5) \end{matrix} \end{matrix}$

式中:E_obs(s)为s时刻无源控制器的观测值; ξ (s)为s时刻无源控制器的耗散因子; Δ t为无源观测器的采样周期。

根据式(3), E_obs(s)可以表示为:

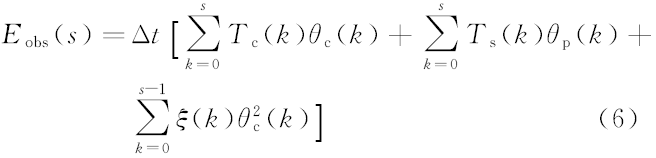
根据式(5)可得到式(7):

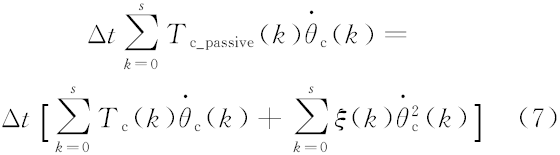
根据式(6)(7)可得:

将式(4)代入式(8)可得式(9):

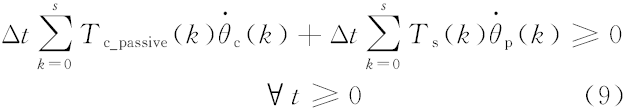
这证明了由式(3)(4)(5)组成的无源控制器可保证系统任一时刻的观测器值非负, 系统是无源的。因此, 当应用SBW系统双向控制结构时, 将力感模拟电机的实际控制转矩T_c经设计的无源控制器变成T_{c_passive}, 可保证系统控制的稳定性。

4 试验验证

SBW系统没有转向盘与转向车轮的机械连接, 目前车辆安全法规是不允许上路的。但对于SBW控制方法研究而言, 模型仿真不易完整体现实际SBW系统参数的非线性和不确定性, 执行元件控制精度、传感器噪声、数据采集精度等也对实车控制系统的设计带来了许多不稳定因素。因此, SBW试验车是验证SBW控制系统的最佳平台。本文使用作者所在研究团队的以国内某品牌的一款紧凑型掀背车为基础改装的线控转向汽车, 如图8所示。

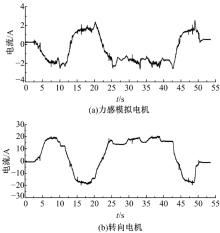
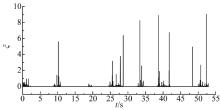
	Figure Option View Download New Window
	图8 线控转向试验车Fig.8 SBW test vehicle

考虑到场地限制和试验安全性, 并能够充分验证上述方法的有效性, 本文进行了驻车转向盘转角随机输入的试验。为了保证转向盘力矩不超过转矩传感器测量范围, 取力传动比α =8, 角传动比β =1, 图9~图11为试验结果曲线。图9为没有稳定性控制时力感模拟电机和转向电机的电流对比曲线。图10为相似转向盘输入下, 具有稳定性控制的电流对比曲线。图11为该工况下, 无源控制器耗散因子ζ 的变化曲线。

	Figure Option View Download New Window
	图9 没有稳定性控制的电机电流对比图Fig.9 Curve of motor current without stability control

	Figure Option View Download New Window
	图10 具有稳定性控制的电机电流对比图Fig.10 Curve of motor current with stability control

	Figure Option View Download New Window
	图11 无源控制器耗散因子的变化曲线Fig.11 Curve of passive controller dissipation factor

从图9和图10可以看出:在没有稳定性控制时, 力感模拟电机和转向电机电流信号噪声较大, 在大扭矩条件下, 驾驶员能够感觉到较为明显的转向盘力矩波动; 采用无源控制器后, 两电机的工作电流噪声明显降低, 转向系统的力矩波动减小。图11表明, SBW系统在大负载情况下容易呈现“ 有源” 状态, 通过无源控制器的调节, 能够保证系统运行的稳定性。

5 结论

(1)线控转向系统本质上是一种具有力觉临场感的双向遥操作控制系统, 针对转向盘模块与转向执行模块间位置与转矩耦合控制时的稳定性问题, 本文提出并使用了转矩驱动/位置反馈式双向控制结构。

(2)通过简化汽车转向系统模型, 证明了机械转向系统是无源的, 借助分析助力转向系统, 分析了线控转向系统的无源、有源状态部分, 确定了可能引起系统控制失稳的输入输出向量。

(3)利用无源观测器考察系统稳定性, 针对线控转向系统易呈现有源状态部分, 设计了无源控制器, 以保证系统的无源性, 完成系统的稳定性控制。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Im J S, Ozaki F, Matsushita T, et al. Experiment study on steer-by-wire system with bilateral control[C]∥Proceedings of International Conference on Mechatronics, Kumamoto, 2007: 1-6. [本文引用:1]
[2]	Raju G. Design issue in 2-port networks models of bilateral remote manipulation[J]. IEEE Transaction on Automatic Control, 1989, 34(3): 1316-1321. [本文引用:1]
[3]	Xi N, Tarn T J. Action synchronization and control of internet based telerobotic systems[C]∥Proceedings of 1999 IEEE International Conference on Robotics and Automation, Detroit MI, 1999: 219-224. [本文引用:1]
[4]	Chopra N, Spong M W, Hirche S, et al. Bilateral teleoperation over the internet: The time varying delay problem[C]∥Proceedings of the 2003 American Control Conference, Denver, CO, 2003: 155-160. [本文引用:1]
[5]	Li H J, Song A G. Virtual-environment modeling and correction for force-reflecting teleoperation with time delay[J]. IEEE Transactions on Industrial Electronics, 2007, 54(2): 1227-1233. [本文引用:1]
[6]	Wang Xiang, Zong Chang-fu, Xing Hai-tao, et al. Bilateral control method of torque drive/angle feedback used for steer-by-wire system[J]. SAE International Journal of Passenger Cars-Electronic and Electrical Systems, 2012, 5(2): 479-485. [本文引用:1]
[7]	邢海涛. 汽车线控转向系统补偿控制方法研究和验证[D]. 长春: 吉林大学汽车工程学院, 2013. Xing Hai-tao. Research on compensation control method for vehicle steer-by-wire system[D]. Changchun: College of Automotive Engineering, Jilin University, 2013. [本文引用:1]
[8]	宗长富, 郑宏宇, 田承伟, 等. 线控转向稳态增益与动态增益反馈校正控制算法[J]. 汽车工程, 2007, 29(8): 686-691. Zong Chang-fu, Zheng Hong-yu, Tian Cheng-wei, et al. Steady-state gain and dynamic feedback correction algorithm for steer-by-wire[J]. Automotive Engineering, 2007, 29(8): 686-691. [本文引用:1]
[9]	Lee D J, Li P Y. Passive bilateral feedforward control of linear dynamically similar teleoperated manipulators[J]. IEEE Transactions on Robotics and Automation, 2003, 19(3): 443-456. [本文引用:1]
[10]	Matsunaga N, Im J, Kawaji S. Control of steering-by-wire system of electric vehicle using bilateral control designed by passivity approach[J]. Journal of System Design and Dynamics, 2010, 4(1): 50-60. [本文引用:1]

2007

0.0

... 0 引言线控转向系统(Steering-by-wire system,SBW)作为一种双向遥操作系统,稳定性不仅是评价其双向控制结构的重要性能,更是所有控制系统的共同要求^[1] ...

1989

0.0

... Raju^[2]首先提出使用二端口网络理论来分析力反馈遥操作机器人系统,得出导致系统不稳定的原因是时延造成了通信环节的有源性 ...

1999

0.0

... Xi等^[3]针对力反馈遥操作机器人的信号传输环节引起的不确定时延问题,提出了基于事件的控制算法,以保证随机时延对系统稳定性的影响 ...

2003

0.0

... Chopra等^[4]通过频域优化技术,提出了阻抗匹配滤波器设计,保证遥操作系统的无源性和透明性 ...

2007

0.0

... Li等^[5]提出了基于操作对象等效阻抗在线估计的自适应无源控制算法,用于保证较大时延下力觉临场感机器人的稳定性 ...

2012

0.0

... 1 线控转向系统转矩驱动/位置反馈式双向控制结构汽车线控转向系统通过控制两个或者更多的电机来控制转向盘和转向车轮,达到对两个模块转角和转矩的耦合控制的目的^[6] ...

2013

0.0

. 2013, :-

Research on compensation control method for vehicle steer-by-wire system[D]. Changchun:College of Automotive Engineering,

汽车线控转向系统补偿控制方法研究和验证[D]

Xing Hai-tao.

邢海涛

传统汽车转向系统一般通过液压助力或者电动助力转向系统帮助驾驶员实现转向，同时需要保证驾驶员对于路面反馈信息的感知。而随着汽车电子电气系统的广泛应用，线控转向系统通过转向电机、传感器和控制单元的集成，可以取代转向系统中的机械部分连接，从而拓展转向系统传动比、刚度和阻尼等方面的设定空间，为获得更好的车辆操纵性和更轻松的驾驶体验提供了条件。本文结合国家自然科学基金项目“线控转向系统操纵杆及其双向控制方法研究”（项目编号：51105165）和“线控汽车底盘控制方法和关键技术研究”（项目编号：50775096），在线控转向整体控制框架、容错控制策略等研究的基础上，结合双向控制结构，针对线控转向系统控制补偿控制方法开展了深入研究。为了使驾驶员获得更清晰的驾驶过程中的路面信息，通过研究转向盘机械结构改变对系统摩擦、阻尼和惯量的影响，制定了适合于线控转向系统的补偿控制方法，可以保证双向控制结构中更好的力觉临场感，并且提高转向轻便性。进行了线控转向汽车的实车改装和电子电气匹配，通过实车实验验证了控制方法的有效性。具体内容如下：（1）通过双向控制方法的理论研究，结合线控转向系统的特点选择力直接反馈-位置型双向控制方法，用来解决力反馈信息的问题。这种方法不需要对于车辆包括车轮状态进行估计，直接通过转向执行电机的转矩/电流和力传动比设置，获得转向盘力反馈电机的目标转矩。双向控制方法在军事和机器人领域的应用证明，线控转向系统这种主从控制结构可以应用在线控转向这种遥操作模式实现转向意图，同时获得更好的力觉临场感，即获得更准确的路面信息。结合双向控制方法，对于转向盘模块进行动力学分析，研究了转向盘模块补偿控制与其动力学特性的联系。（2）在研究力传动比和角传动比设置的双向控制方法基础上，重点研究了线控转向系统的补偿控制方法。借鉴电动助力转向系统转向盘力感的设计方法，设计了本系统关于车速和转向执行电机转矩的力传动比。同时力传动比可以根据驾驶员驾驶习惯进行修正。在角传动比方面，采用可以根据工况和驾驶员习惯设定的定传动比。在补偿控制方法上，对于转向盘部分作为整体进行了摩擦、阻尼和惯量补偿，避免了分块分析带来的参数估计和等价转换的复杂计算。摩擦补偿以转向盘转角和力反馈转矩为输入信号，通过合理配置参数，提高摩擦补偿的响应速度，并解决动静摩擦转换的问题。为获得控制参数中的最大静摩擦值，采用分离转向盘模块的实验方法。阻尼补偿主要针对低速行驶工况，以转向盘转速为输入信号，保证转向盘转速较大时不会产生过大的阻尼转矩。研究时考虑了阻尼补偿抵抗干扰的能力。惯量补偿采用转矩微分前馈的方法，对比采用转向盘角加速度作为信号输入，信号的精度较高。对于线控转向系统的补偿控制可以提高转向系统的轻便性和回正性，在一定程度上会减轻驾驶员的疲劳，并且驾驶员获得清晰的路面信息。（3）结合实验条件和控制方法实现的要求，进行线控转向车辆改装和电子电气设备匹配工作。应用单片机控制力反馈电机和转向执行电机，采用xPC Target快速原型技术实现控制信号的传输和数据采集。（4）对线控转向控制策略和补偿控制方法进行实车实验验证。针对线控转向汽车双向控制方法和补偿控制方法的验证的需要，提出需要进行的实验内容。为验证线控转向双向控制策略的有效性，进行了转向盘正弦输入的原地和低速实验。在确定角传动比条件下，转向执行机构的小齿轮对转向盘转角的跟随性能较好。同时转向盘转矩比较理想，验证了双向控制力反馈设计和力传动比设置的合理性。为了验证补偿控制方法，将转向盘模块与转向执行模块分离考虑，逐步进行摩擦、阻尼和惯量补偿控制方法的设计，减小由于转向盘模块自身摩擦、阻尼和惯量影响的转向盘转动时的转矩。实车实验证明，采用补偿控制方法后，在低速回正工况中，回正较快而且转向盘残留角减小，提高了线控汽车的回正性能；在双纽线工况中转向盘转矩减小，提高了车辆的轻便性。

... 的控制思想^[7,8]:转向盘模块采用位置闭环控制,控制目标为小齿轮转角与SBW轴间角传动比之积,状态反馈为转向柱的转角,扰动输入为转向盘力矩 ...

2007

0.0

. 2007, 29(8):686-691 DOI:doi:10.3321/j.issn:1000-680x.2007.08.012

Steady-state gain and dynamic feedback correction algorithm for steer-by-wire

线控转向稳态增益与动态增益反馈校正控制算法

Zong Chang-fu , Zheng Hong-yu , Tian Cheng-wei

宗长富, 郑宏宇, 田承伟

以29自由度汽车动力学模型为基础,提出了保证线控汽车转向增益不变的稳态控制策略,使线控汽车转向特性不随车速和转向盘转角变化;提出了基于状态反馈的动态校正稳定性控制算法.仿真和驾驶模拟器实验表明,基于转向增益不变的稳态控制策略保证了汽车转向特性不变,减轻了驾驶员的负担,适合于更多的驾驶人群;基于状态反馈的动态校正稳定性控制算法有效提高了汽车的稳定性.

... 的控制思想^[7,8]:转向盘模块采用位置闭环控制,控制目标为小齿轮转角与SBW轴间角传动比之积,状态反馈为转向柱的转角,扰动输入为转向盘力矩 ...

2003

0.0

... y的映射是无源的^[9] ...

2010

0.0

... 因此,机械转向系统是一种二端口的网络系统^[10],且对于驾驶员力矩输入和转向阻力矩输入来说,是无源的 ...