基于<em> H</em><sub>∞</sub>的车辆横向运动鲁棒控制

引用本文

钱立军, 胡伟龙, 辛付龙, 邱利宏. 基于 H_∞的车辆横向运动鲁棒控制 . 2015, 45(6): 1757-1762
QIAN Li-jun, HU Wei-long, XIN Fu-long, QIU Li-hong. Controlling of vehicle lateral movement based on robust H_∞ theory . Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1757-1762 复制到剪切板

Permissions

基于 H_∞的车辆横向运动鲁棒控制

钱立军, 胡伟龙, 辛付龙, 邱利宏

合肥工业大学机械与汽车工程学院 ,合肥 230009

作者简介:钱立军(1962-),男,教授,博士生导师.研究方向:车辆电子,车辆控制.E-mail:hfutqlj@163.com

基金:工信部电子产业发展基金项目(财[2009]453号); 中航工业产学研合作创新工程项目(CXY2010HFGD26)

摘要

为了实现车辆在横向运动过程中的精确控制,提出了一种车辆横向运动鲁棒控制器。通过控制输入转向系统控制器中转角的大小得到理想的车辆质心横向加速度,实现鲁棒稳定和较小的控制误差。首先根据车辆二自由度模型、转向系统摄动、道路摄动建立广义状态方程,再对广义状态方程进行回路变换,求出控制器,最后进行稳定性分析和试验验证。所得的控制器参数随车速变化而变化,且控制器的设计比其他的变参数控制器设计要简单。稳定性分析结果表明,控制器使得系统内部稳定;实车验证结果表明,控制器能够使车辆横向运动的质心加速度误差控制在0.1 m/s²以内。

关键词: 车辆工程; 鲁棒控制; 横向运动; 摄动; 内部稳定

中图分类号:U27 文献标志码:A 文章编号:1671-5497(2015)06-1757-06

Controlling of vehicle lateral movement based on robust H_∞ theory

QIAN Li-jun, HU Wei-long, XIN Fu-long, QIU Li-hong

School of Mechanical and Automotive Engineering, Hefei University of Technology,Hefei 230009,China

Abstract

In order to achieve precise control of the lateral movement of vehicles, a robust controller for vehicle motion is proposed. Ideal lateral acceleration of the vehicle mass center is achieved by changing the input angle of the steering controller, and robust stability and smaller control error are obtained. First, according to 2-degree-freedom vehicle model, the steering system and road perturbations, the generalized state equation is established. Then a loop transformation of the state equation is made to get the controller. Finally stability analysis and experiments are carried out. The controller parameters vary with the vehicle speed, and the design of this controller is much simpler than other variable parameter controller. Stability analysis results show that the whole control system has internal stability. Vehicle experiment results show that the controller can make the acceleration error of the lateral motion of the vehicle mass center within 0.1 m/s².

Keyword: vehicle engineering; robust control; lateral movement; perturbation; internal stability

Show Figures

0 引言

车辆横向运动控制方法分为预瞄式和非预瞄式。预瞄式以期望航向和当前航向之差作为偏差建立控制器, 必须提前知道大量道路信息, 对车辆获取外部环境信息的能力提出了过高的要求^{[1, 2, 3, 4]}; 非预瞄式通过期望路径和车辆运动学模型计算出描述车辆运动的动力学物理量大小, 如车辆横摆角速度, 然后设计反馈控制系统进行控制。由于车辆是一个时变、非线性系统, 文献[5-8]设计了基于模糊逻辑、遗传算法和滑模控制理论的一些控制器来解决参数时变问题。这些控制器设计复杂、计算量大。其实在自主泊车、无人驾驶等工况中, 在很短的时间内车辆的速度变化不大。设计一种控制器, 在不同速度间变化时, 不一定收敛, 在具体的某个速度值时, 一定收敛, 可以减少运算量和减轻控制难度。

本文采用非预瞄式控制方法, 考虑车辆转向系统的结构摄动和路面的外部摄动^[9], 以输入转向系统控制器的转角(即期望转角)为输入量, 以车辆质心横向加速度为输出量建立随车速变化的转向系统模型, 在不同速度区间内设计和当前速度区间有关的鲁棒控制器。使得车辆在横向运动中, 可以通过改变输入转向系统控制器中的转角得到想要的车辆质心横向加速度。这种控制器具有设计简单、运算量小且鲁棒稳定性好和误差较小的优点。

1 车辆横向运动模型的建立

1.1 车辆运动状态方程

建立车辆二自由度运动模型如下:

$\begin{matrix} \{\begin{matrix} mv (\overset{\cdot}{β} + r_{w}) + k_{1} k_{2} β - \\ r_{w} (a k_{1} - b k_{2}) / v = k_{1} δ \\ I_{zw} {\overset{\cdot}{r}}_{w} + (a k_{1} - b k_{2}) β + \\ r_{w} (a^{2} k_{1} + b^{2} k_{2}) / v = a k_{1} δ \end{matrix} (1) \end{matrix}$

式中:I_z_w为绕z轴的转动惯量; m为车辆质量; r_w为横摆角速度; β 为质心横偏角; a、b分别为前后轮轴到车辆重心的距离; k₁、k₂分别为前后轮的横偏刚度; v为汽车行驶速度; δ 为前轮转角。

定义车辆重心处的横向加速度为α _l, 有:

$\begin{matrix} y = a_{l} = v (\overset{\cdot}{β} + r_{w}) (2) \end{matrix}$

定义从前轮转角δ 到加速度y的传递函数为p₁(s), 以[β , r_w]为状态变量, δ 为输入变量, y为输出变量, 有系统p₁(s)的状态方程如下:

$\begin{matrix} [\begin{matrix} \overset{\cdot}{β} \\ {\overset{\cdot}{r}}_{w} \\ y \end{matrix}] = [\begin{matrix} - \frac{k_{1} k_{2}}{mv} & \frac{a k_{1} - b k_{2}}{m v^{2}} \\ - \frac{a k_{1} - b k_{2}}{I_{z}} & - \frac{a^{2} k_{1} + b^{2} k_{2}}{I_{z} v} \\ - \frac{k_{1} k_{2}}{m} & \frac{a k_{1} - b k_{2} + m v^{2}}{mv} \end{matrix} \begin{matrix} \frac{k_{1}}{mv} \\ \frac{a k_{1}}{I_{z}} \\ \frac{k_{1}}{m} \end{matrix}] [\begin{matrix} β \\ r_{w} \\ δ \end{matrix}] (3) \end{matrix}$

1.2 转向系统状态方程

考虑转向系统对前轮转角的影响。一般转向执行器模型包括电子和机械两部分, 分析起来较为困难。采用系统辨识的方法来确认转向系统模型^{[10, 11]}, 通过大量的试验和数据, 用最小二乘辨识算法可以得到期望前轮转角δ _d和前轮转角δ 之间满足:

$\begin{matrix} p_{2} (s) = \frac{δ}{δ_{d}} = \frac{b}{s^{2} + 10 s + a} (4) \end{matrix}$

式中:a∈ [12, 20]; b∈ [1, 5]。

图1为在某一动作序列下的辨识结果, 可见得到的模型是非常切合实际的。

	Figure Option View Download New Window
	图1 系统辨识的结果Fig.1 Result of system identification

令a=16+aΔ ₁; $\begin{matrix} |Δ_{1}| \end{matrix}$ < 1; b=3+2Δ ₂; $\begin{matrix} |Δ_{2}| \end{matrix}$ < 1, 则传递函数p₂可以表示成图2所示模型。由图2可以得到转向系统状态方程(5)(6), 其中期望前轮转角δ _d就是实际输入到转向系统控制器中的前轮转角。

	Figure Option View Download New Window
	图2 传递函数p₂模型Fig.2 Model of transfer function p₂

$\begin{matrix} \begin{matrix} {[\begin{matrix} z_{1} & z_{2} & δ \end{matrix}]}^{T} = \\ [\begin{matrix} \frac{4}{(s + 2) (s + 8)} & \frac{1}{(s + 2) (s + 8)} & \frac{3}{(s + 2) (s + 8)} \\ 0 & 0 & 2 \\ \frac{4}{(s + 2) (s + 8)} & \frac{1}{(s + 2) (s + 8)} & \frac{3}{(s + 2) (s + 8)} \end{matrix}] \times \\ {[\begin{matrix} w_{1} & w_{2} & δ_{d} \end{matrix}]}^{T} (5) \\ [\begin{matrix} z_{1} \\ z_{2} \end{matrix}] = [\begin{matrix} Δ_{1} & 0 \\ 0 & Δ_{2}^{} \end{matrix}] [\begin{matrix} w_{1} \\ w_{2} \end{matrix}] (6) \end{matrix} \end{matrix}$

1.3 路面不平度的影响

考虑路面不平度对z_g车辆重心处横向加速度的影响, 通过大量计算得到经验公式如下:

$\begin{matrix} a_{l 1} = a_{l} (1 + z_{g} \sqrt{\frac{0.2 ζ}{H} + \frac{0.1 {u_{h}}^{2} u_{g}}{2 {k_{α}}^{2} + {u_{h}}^{2} G (q)}}) (7) \end{matrix}$

式中:α _l1为考虑路面不平度后的车辆重心处横向加速度; z_g为路面垂向位移; G(q)为路面系数; u为路面附着系数; u_h、u_g分别为横向、垂向附着系数; H为常数; k_α为轮胎横偏刚度; ζ 为与轮胎有关的系数。

假设路面为一般路面, 路面的垂直位移幅度为1~200 mm, 定义:

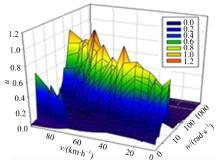
$\begin{matrix} \begin{matrix} z_{g} = 0.2 Δ_{3}, |Δ_{3}| < 1 \\ \sqrt{\frac{0.2 ζ}{H} + \frac{0.1 {u_{H}}^{2} ug}{2 {k_{α}}^{2} + {u_{H}}^{2} G (q)}} = E (8) \end{matrix} \end{matrix}$

则α _l1可以表示成如图3所示。

	Figure Option View Download New Window
	图3 路面不平影响模型Fig.3 Model of the road uneven impact

由图3可得到如式(9)所示的状态方程。

$\begin{matrix} \begin{matrix} [\begin{matrix} z_{3} \\ a_{l 1} \end{matrix}] = [\begin{matrix} 0 & 0.2 E \\ 1 & 1 \end{matrix}] [\begin{matrix} w_{3} \\ a_{l} \end{matrix}] (9) \\ w_{3} = Δ_{3} z_{3} (10) \end{matrix} \end{matrix}$

1.4 前轮转角-质心横向加速度的广义传递函数

令y为车辆重心处实际横向加速度, δ _d为输入变量, 由式(3)(5)(6)(9)(10)可得从输入转向系统控制器的前轮转角到车辆质心处实际横向加速度之间的广义传递函数为:

$\begin{matrix} \begin{matrix} [\begin{matrix} \overset{\cdot}{β} \\ {\overset{\cdot}{r}}_{w} \\ z_{1} \\ z_{2} \\ z_{3} \\ y \end{matrix}] = M [\begin{matrix} β \\ r_{w} \\ w_{1} \\ w_{2} \\ w_{3} \\ δ_{d} \end{matrix}] = [\begin{matrix} A & B_{1} & B_{2} \\ C_{1} & D_{11} & D_{12} \\ C_{2} & D_{21} & D_{22} \end{matrix}] [\begin{matrix} β \\ r_{w} \\ w_{1} \\ w_{2} \\ w_{3} \\ δ_{d} \end{matrix}] (11) \end{matrix} \end{matrix}$

式中：

$[\begin{matrix} w_{1} \\ w_{2} \\ w_{3} \end{matrix}] = [\begin{matrix} Δ_{1} & 0 & 0 \\ 0 & Δ_{2} & 0 \\ 0 & 0 & Δ_{3} \end{matrix}] [\begin{matrix} z_{1} \\ z_{2} \\ z_{3} \end{matrix}] (12)$

$\begin{matrix} M = [\begin{matrix} - \frac{k_{1} k_{2}}{mv} & \frac{a k_{1} - b k_{2}}{m v^{2}} & \frac{4 k_{1}}{mv (s + 2) (s + 8)} & \frac{k_{1}}{mv (s + 2) (s + 8)} & 0 & \frac{3 k_{1}}{mv (s + 2) (s + 8)} \\ - \frac{a k_{1} - b k_{2}}{I_{z}} & \frac{a^{2} k_{1} + b^{2} k_{2}}{I_{z} v} & 0 & 0 & 0 & \frac{2 a k_{1}}{I_{z}} \\ 0 & 0 & \frac{4}{(s + 2) (s + 8)} & \frac{1}{(s + 2) (s + 8)} & 0 & \frac{3}{(s + 2) (s + 8)} \\ 0 & 0 & 0 & 0 & 0 & 2 \\ - \frac{0.2 k_{1} k_{2} E}{m} & \frac{0.2 E (a k_{1} - b k_{2} + m v^{2})}{mv} & \frac{0.8 E k_{1}}{m (s + 2) (s + 8)} & \frac{0.2 E k_{1}}{m (s + 2) (s + 8)} & 0 & \frac{0.6 E k_{1}}{m (s + 2) (s + 8)} \\ - \frac{k_{1} k_{2}}{m} & \frac{a k_{1} - b k_{2} + m v^{2}}{mv} & \frac{4 k_{1}}{m (s + 2) (s + 8)} & \frac{k_{1}}{m (s + 2) (s + 8)} & 1 & \frac{3 k_{1}}{m (s + 2) (s + 8)} \end{matrix}] (13) \end{matrix}$

2 设计H_∞输出反馈控制器

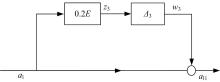
空间状态M是个开环广义控制系统, 需要设计一种控制器K使得系统稳定。分析系统发现, 系统中含有结构确定性摄动Δ ₁、Δ ₂和结构不确定性摄动Δ ₃。采用鲁棒控制器中的空间状态H_∞输出反馈控制来设计控制器K^{[12, 13]}, 结构见图4。

	Figure Option View Download New Window
	图4 H_∞输出反馈控制Fig.4 The H_∞ output feedback control

2.1 判断M是否满足H_∞输出反馈控制设计的条件

对于任意的Re s≥ 0有rank[sI-A B₁]=rank A, 满足(A, B₁)是可稳定的;

对于任意的Re s≥ 0有rank[sI-A C₁]^T=rank A, 满足(C₁, A)是可检测的;

对于任意的Re s≥ 0有rank[sI-A B₂]=rank A, 满足(A, B₂)是可稳定的;

对于任意的Re s≥ 0有rank[sI-A C₂]^T=rank A, 满足(C₂, A)是可检测的^[14];

但是D₁₁≠ 0, D₂₂≠ 0, 不满足D₁₁=0, D₂₂=0的条件。

2.2 对M回路变换以满足H_∞输出反馈控制设计的条件

对于D₁₁≠ 0和D₂₂≠ 0, 不能进行控制器的设计, 需要通过回路变换化为等价标准型D₁₁=0和D₂₂=0。对于D₂₂=0, 只要将D₂₂作为反馈归入控制器K即可, 此时得到新的控制器 $\begin{matrix} \bar{K} \end{matrix}$ 。

$\begin{matrix} \begin{matrix} \bar{M} = [\begin{matrix} A & B_{1} & B_{2} \\ C_{1} & D_{11} & D_{12} \\ C_{2} & D_{21} & 0 \end{matrix}] (14) \\ \bar{K} = K (I - D_{22} {K)}^{- 1} (15) \end{matrix} \end{matrix}$

对于D₁₁≠ 0, 引入新的控制系统如图5所示, 其中:

$\begin{matrix} \begin{matrix} N (D_{11}) = [\begin{matrix} N_{11} & N_{12} \\ N_{21} & N_{22} \end{matrix}] = \\ γ^{- 1} [\begin{matrix} γ^{- 1} {\overset{ˇ}{D}}_{11} & (I - γ^{- 2} {\overset{ˇ}{D}}_{11} {\overset{ˇ}{D}}_{11}^{*})^{\frac{1}{2}} \\ - (I - γ^{- 2} {\overset{ˇ}{D}}_{11} {\overset{ˇ}{D}}_{11}^{*})^{\frac{1}{2}} & γ^{- 1} {\overset{ˇ}{D}}_{11}^{*} \end{matrix}], \end{matrix} \end{matrix}$

且γ > ‖ $\begin{matrix} {\overset{ˇ}{D}}_{11} \end{matrix}$ ‖ ; $\begin{matrix} \tilde{M} \end{matrix}$ =F_l(M, $\begin{matrix} F_{\infty} \end{matrix}$ ); $\begin{matrix} \overset{ˇ}{M} \end{matrix}$ =F_l(N, $\begin{matrix} \tilde{M} \end{matrix}$ ); $\begin{matrix} \overset{ˇ}{M} \end{matrix}$ =F_l( $\begin{matrix} \overset{ˇ}{M} \end{matrix}$ , $\begin{matrix} {\overset{ˇ}{D}}_{22} \end{matrix}$ ); $\begin{matrix} F_{\infty} \end{matrix}$ = $\begin{matrix} U_{\infty} \end{matrix} \begin{matrix} (I + D_{22} U_{\infty})^{- 1} \end{matrix}$ ; $\begin{matrix} U_{\infty} \end{matrix}$ =- $\begin{matrix} D_{12}^{*} \end{matrix}$ D₁₁ $\begin{matrix} [I + \tilde{D_{⊥}^{*}} (γ^{2} I - (D_{⊥}^{*} D_{11} {\tilde{D_{⊥}^{*}})}^{*} \times \end{matrix} \begin{matrix} (D_{⊥}^{*} D_{11} {\tilde{D_{⊥}^{*}}))}^{- 1} (D_{⊥}^{*} D_{11} {\tilde{D_{⊥}^{*}})}^{*} D_{⊥}^{*} D_{11}] \end{matrix} \begin{matrix} D_{21}^{*} \end{matrix}$ 。

	Figure Option View Download New Window
	图5 回路变化后的控制系统Fig.5 Control system after Loop changing

2.3 H_∞输出反馈控制器K_∞

车辆相关参数如下:车辆质量为2200 kg; 前轮横偏刚度为6× 10⁴ N· rad^-1; 绕Z轴转动惯量为3300 kg· m²; 质心到前轴距离为1.34 m; 质心到后轴距离为1.29 m; E为1.67。按照上述方法, 利用Matlab的鲁棒控制工具箱得到H_∞输出反馈控制器K_∞如式(16)所示。可以看出, 控制器随着车速的变化而变化。

$\begin{matrix} K_{\infty} = [\begin{matrix} \frac{1.367}{v} & \frac{5.367 v + 5.667}{v^{2}} & 1.67 & 5.78 & 2.5 v & \frac{3.56}{v (s + 2)} \\ 0 & 2.57 s (v^{2} + 1.34 vs) & 9.67 & 0 & 1.78 & 6 \\ 0.2749 s^{2} v^{2} & 0 & 0 & 0 & 0 & 2.8 \\ 0 & 4.67 & 0 & 0 & 0 & 0 \\ \frac{0.998 (1.89 vs + v^{2})}{v (s + 8)} & 0 & 0 & 0 & 0 & 2.66 vs + v^{2} \\ \frac{2.58}{v} & 1.78 s & 1.8 v & 0.67 & 0 & 2.66 vs \end{matrix}] (16) \end{matrix}$

3 仿真试验

3.1 系统的稳定性

由于摄动‖ Δ ‖ _∞< γ ^-¹, 定义γ =1, 则根据控制系统鲁棒稳定性定理^{[15, 16]}, 可以得到在车辆横向运动系统为内部稳定的充要条件为控制系统的最大奇异值小于1, 即:

$\begin{matrix} \sup_{w \in R, v \in R} u_{Δ} [F_{l} (\hat{M}, \hat{K})] \leq 1 \end{matrix}$

图6为控制系统在不同速度下各个频率的奇异值。由图6可以看出, 奇异值都在1下方, 即整个系统是良定和内部稳定的。

	Figure Option View Download New Window
	图6 控制系统在不同速度下各个频率的奇异值Fig.6 Singular value of control system under different frequency and different speeds

3.2 有无控制器时的系统误差

设定初始横摆角速度r_w为0, 初始质心横偏角β 为0, Δ ₁=sint, Δ ₂=sin2t, Δ ₃=cost, 分别进行仿真和试验。在车速v为30、50、80 km/h时, 得到无控制器仿真的车辆横向加速度y₁和实际车辆横向加速度Y₁之间的误差Δ _y₁随车辆前轮期望转角δ _d的变化关系, 以及有控制器K时车辆的横向加速度y₂和实际测得的车辆横向加速度Y₂之间的误差Δ _y₂随车辆前轮期望转角δ _d的变化关系, 如图7所示。

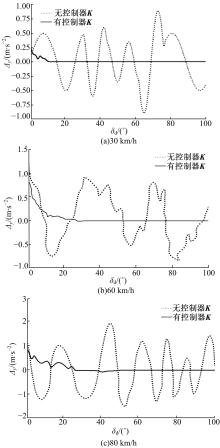	Figure Option View Download New Window
	图7 无控制器的Δ _y₁及有控制器的Δ _y₂随车辆前轮期望转角δ _d的变化关系Fig.7 Relationship of Δ _y₁and δ _d and The relationship of Δ _y₂ and δ _d

从图7可以看出:有控制器时, 被控系统仿真值和试验值的误差在前轮转角变化一段时间后进入0附近的一个很小的范围, 因此为一致最终有界; 无控制器时, 被控系统仿真值和试验值的误差在外部干扰下呈不稳定状态, 误差比较大。随着车速的增大, 误差也在不断增大, 这与实际情况也是相符的。

综上所述, 控制器K_∞使车辆在横向运动中且处于多种外部干扰下, 仍然可以通过改变输入转向系统控制器中的转角得到期望的车辆质心横向加速度, 并且实际质心加速度和期望的质心加速度间的差距很小, 稳定后在0.1 m/s²以内, K_∞控制器使得系统实现鲁棒稳定性和较小的误差。

4 结束语

通过对车辆横向运动模型进行研究, 建立从前轮转角到质心横向加速度的状态方程。通过对状态方程的控制器进行回路变化, 求解出输出反馈控制器。该控制器使得车辆在泊车、低速无人驾驶等工况下的横向运动获得了鲁棒稳定性和较小的误差。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	王家恩, 陈无畏, 王檀彬, 等. 基于期望横摆角速度的视觉导航智能车辆横向控制[J]. 机械工程学报, 2012, 48(4): 108-112. Wang Jia-en, Chen Wu-wei, Wang Tan-bin, et a1. Vision guided intenigent vehicle lateral control based on desired yaw rate[J]. Journal of Mechnical Engineering, 2012, 48(4): 108-112. [本文引用:1]
[2]	丁海涛, 郭孔辉, 李飞, 等. 基于加速度反馈的任意道路和车速跟随控制驾驶员模型[J]. 机械工程学报, 2010, 46(10): 116-120. Ding Hai-tao, Guo Kong-hui, Li Fei, et a1. Arbitrary path and speed following driver model based on vehicle acceleration feedback[J]. Journal of Mechnical Engineering, 20l0, 46(10): 116-120. [本文引用:1]
[3]	赵熙俊, 陈慧岩. 智能车辆路径跟踪横向控制方法的研究[J]. 汽车工程, 2011, 33(5): 384-387. Zhao Xi-jun, Chen Hui-yan. A study on lateral control method for the path tracking of intelligent vehicles[J]. Automotive Engineering 2011, 33(5): 384-387. [本文引用:1]
[4]	Yacine Z, Ichalal D, Ait-Oufroukh N, et a1. Takagi-Sugeno observers: experimental application for vehicle lateral dynamics estimation[J]. Control Systems Technology, 2014, 99(6): 1-8. [本文引用:1]
[5]	王吉华, 魏民祥, 李玉芳, 等. 多轴转向车辆模糊H_∞保性能控制[J]. 南京航空航天大学学报, 2013, 45(10): 677-682. Wang Ji-hua, Wei Min-xiang, Li Yu-fang, et al. T-S fuzzy H_∞ guaranteed cost control of multi-steering vehicle[J]. Journal of Nanjing University of Aeronautics & Astronautics, 2013, 45(10): 677-682. [本文引用:1]
[6]	Zhang Bo-jun, Liu Chun-hui. Modeling and simulating research of integrated fuzzy control for automobile steering stability[C]∥2011 International Conference on Energy and Environmental Scinence, Singapore, 2011: 1299-1304. [本文引用:1]
[7]	Ailon A, Zohar I. Control strategies for driving a group of nonholonomic kinematical mobile robots in formation along a time-parameterized path[J]. IEEE/ASME Transaction on Mechatronics, 2012, 17(2): 326-336. [本文引用:1]
[8]	Li Y H, Zheng Q. Design of robust sliding mode with disturbance observer for multi-axis coordinated traveling system[J]. Computers and Mathematics with Application, 2012, 64(5): 759-765. [本文引用:1]
[9]	贺宜, 褚端峰, 吴超仲, 等. 路面附着条件对车辆横向稳定性影响的量化分析[J]. 武汉理工大学学报: 交通科学与工程版, 2014, 38(4): 784-788. He Yi, Chu Duan-feng, Wu Chao-zhong, et a1. Quantitative analysis of influence on vehicular lateral stability by road surface condition[J]. Journal of Wuhan University of Technology (Transportation Science & Engineering), 2014, 38(4): 784-788. [本文引用:1]
[10]	Le T P, Stiharu I. Preview control and Kalman filter applied to lateral and longitudinal planning for autonomous vehicles[C]∥Proceedings of the 3rd IASTED Asian Conference on Modelling, Identification, and Control, AsiaMIC, 2013: 799-811. [本文引用:1]
[11]	Lin L H, Yen J Y, Wang F C. System identification and robust control of a pneumatic muscle actuator system[C]∥2nd International Conference on Engineering and Technology Innovation, Taiwan, 2013, 284-287: 1936-1940. [本文引用:1]
[12]	He Y, Wu M, She J H. Improved bounded-real-lemma representation and H_∞ control for systems with polytypic uncertainties[J]. IEEE Transactions on Circuits and Systems II: Express Briefs, 2005, 52(7): 380-383. [本文引用:1]
[13]	Xie L, Fridman E, Shaked U. Robust H_∞ control of distributed delay systems with application to combustion control[J]. IEEE Trans Automatic Control, 2001, 46(12): 1930-1935. [本文引用:1]
[14]	刘康志, 姚郁. 线性鲁棒控制[M]. 1版. 北京: 科学出版社, 2013. [本文引用:1]
[15]	吴敏, 桂卫华, 何勇. 现代鲁棒控制[M]. 2版. 长沙: 中南大学出版社, 2008. [本文引用:1]
[16]	玄圣夷, 宋传学, 靳立强, 等. 基于多级鲁棒PID控制的汽车稳定性控制策略[J]. 吉林大学学报: 工学版, 2010, 40(1): 13-18. Xuan Sheng-yi, Song Chuan-xue, Jin Li-qiang, et al. Multilevel robust PID control strategy for vehicle stability control[J]. Journal of Jilin University(Engineering and Technology Edition), ,2010, 40(1): 13-18. [本文引用:1]

2012

0.0

. 2012, 48(4):108-112 DOI:doi:10.3901/JME.2012.04.108

Wang Tan-bin,et a1.Vision guided intenigent vehicle lateral control based on desired yaw rate

基于期望横摆角速度的视觉导航智能车辆横向控制

Wang Jia-en , Chen Wu-wei

王家恩, 陈无畏, 王檀彬

针对采用传统位置偏差控制方法的车道保持系统横向控制精度不高以及鲁棒性差等问题,提出一种跟踪期望横摆角速度的车辆横向控制方法。在车辆当前行驶位置和道路预瞄点之间实时规划逼近目标路径的虚拟路径,同时分析当前时刻车辆以无偏差形式沿此虚拟路径行驶时决定车辆行驶位置的横摆角速度及速度之间的关系。结合车辆道路相对位置及车身状态信息,设计期望横摆角速度生成器。基于7自由度非线性车辆动力学模型,设计滑模控制器跟踪期望横摆角速度,使得车辆稳定地跟踪目标路径。根据车道线宽度和边缘点数量统计进行边缘检测,能有效识别模糊车道边缘和抑制噪声,并通过对消失点的检测来有效去除非车道线的干扰。仿真及试验结果表明,与传统的位置偏差控制方法相比,期望横摆角速度法不仅能提高车辆横向控制的精确性且跟随偏差随车辆速度及道路曲率的变化波动范围小,具有很好的鲁棒性和自适应性。

... 预瞄式以期望航向和当前航向之差作为偏差建立控制器,必须提前知道大量道路信息,对车辆获取外部环境信息的能力提出了过高的要求^[1,2,3,4] ...

2010

0.0

. 2010, 46(10):116-120 DOI:doi:10.3901/JME.2010.10.116

Arbitrary path and speed following driver model based on vehicle acceleration feedback

基于加速度反馈的任意道路和车速跟随控制驾驶员模型

Ding Hai-tao , Guo Kong-hui , Li Fei

丁海涛, 郭孔辉, 李飞

建立一个高效的能够适应复杂汽车行驶工况的驾驶员模型是进行"人-车-路"闭环仿真的关键.利用离散的数表方式对驾驶员跟随的任意道路路径和车速进行描述.以此为基础,提出任意路径下的预瞄点搜索算法,使"预瞄-跟随"驾驶员建模理论可应用于任意道路路径和车速的跟随控制.根据车速变化不断更新侧向加速度增益,实现驾驶员模型方向控制和速度控制的解耦.通过引入加速度反馈,建立一个简单而有效的跟随任意道路路径和车速的方向与速度综合控制驾驶员模型.仿真表明该驾驶员模型具有良好的路径与车速跟随精度.

... 预瞄式以期望航向和当前航向之差作为偏差建立控制器,必须提前知道大量道路信息,对车辆获取外部环境信息的能力提出了过高的要求^[1,2,3,4] ...

2011

0.0

. 2011, 33(5):384-387

A study on lateral control method for the path tracking of intelligent vehicles

智能车辆路径跟踪横向控制方法的研究

Zhao Xi-jun , Chen Hui-yan.

赵熙俊, 陈慧岩

提出了一种智能车辆的路径跟踪横向控制系统.系统由期望航向偏差生成器和反馈控制系统两部分组成.期望航向偏差根据车辆-道路之间运动学关系来确定;而反馈控制系统则采用基于车辆-道路动力学模型的鲁棒PID控制器.在分析系统特性的基础上设计以某一速度为基准的、ITAE性能指标最优的固定增益鲁棒PID控制器和前置滤波器.在分析纵向速度对反馈系统影响的前提下,给出固定增益PID参数所适用的车速范围;分析了PID参数对闭环反馈系统的影响,调整了其他车速区间的PID参数.实车试验验证的结果表明,所提出的路径跟踪横向控制系统具有良好的路径跟踪能力.

... 预瞄式以期望航向和当前航向之差作为偏差建立控制器,必须提前知道大量道路信息,对车辆获取外部环境信息的能力提出了过高的要求^[1,2,3,4] ...

2014

0.0

... 预瞄式以期望航向和当前航向之差作为偏差建立控制器,必须提前知道大量道路信息,对车辆获取外部环境信息的能力提出了过高的要求^[1,2,3,4] ...

2013

0.0

2011

0.0

2012

0.0

2012

0.0

2014

0.0

. 2014, 38(4):784-788 DOI:doi:10.3963/j.issn.2095-3844.2014.04.018

Quantitative analysis of influence on vehicular lateral stability by road surface condition

路面附着条件对车辆横向稳定性影响的量化分析

He Yi , Chu Duan-feng , Wu Chao-zhong

贺宜, 褚端峰, 吴超仲

摘　要：采用侧翻稳定性指标LTR值和侧滑稳定性指标EG值,定量分析路面附着系数对车辆横向稳定性的影响.同时,通过多组不同路面附着条件下的车辆动力学仿真实验,找出车辆发生侧滑、侧翻事故时路面附着系数的取值范围.结果表明：在车辆结构参数、车速和转向输入等条件恒定的情况下,路面附着系数与车辆侧翻稳定性呈负相关,与车辆侧滑稳定性呈正相关.在鱼钩仿真工况下,当路面附着系数增大至0.75时, 车辆发生侧翻的可能性急剧增大;当附着系数在0.7以下时,车辆发生侧翻的可能性急剧降低;在双移线仿真工况下,当路面附着系数小于0.4时,车辆易失控而发生侧滑现象,但基本不会发生侧翻现象.

... 本文采用非预瞄式控制方法,考虑车辆转向系统的结构摄动和路面的外部摄动^[9],以输入转向系统控制器的转角(即期望转角)为输入量,以车辆质心横向加速度为输出量建立随车速变化的转向系统模型,在不同速度区间内设计和当前速度区间有关的鲁棒控制器 ...

2013

0.0

... 采用系统辨识的方法来确认转向系统模型^[10,11],通过大量的试验和数据,用最小二乘辨识算法可以得到期望前轮转角#cod#x003b4 ...

2013

0.0

... 采用系统辨识的方法来确认转向系统模型^[10,11],通过大量的试验和数据,用最小二乘辨识算法可以得到期望前轮转角#cod#x003b4 ...

2005

0.0

... 输出反馈控制来设计控制器K^[12,13],结构见图4 ...

2001

0.0

... 输出反馈控制来设计控制器K^[12,13],结构见图4 ...

2013

0.0

... 0有rank[sI-A C₂]^T=rank A,满足(C₂,A)是可检测的^[14] ...

2008

0.0

. 2008, :-

吴敏, 桂卫华, 何勇

... =1,则根据控制系统鲁棒稳定性定理^[15,16],可以得到在车辆横向运动系统为内部稳定的充要条件为控制系统的最大奇异值小于1,即: ...

2010

0.0

. 2010, 40(1):13-18

Multilevel robust PID control strategy for vehicle stability control

基于多级鲁棒PID控制的汽车稳定性控制策略

Xuan Sheng-yi , Song Chuan-xue , Jin Li-qiang

玄圣夷, 宋传学, 靳立强

A model was built for the vehicle and its hydraulic brake system using the AMESim software. A PID control algorithm based on the H∞ control theory was used in study of the vehicle stability control. The parameters of the robust PID controller were adjusted according to the vehicle driving state, taking the yaw rate and the mass center sideslip angle as the control targets, an algorithm for the vehicle stability control was developed. Using the PID control algorithm, the brake pressure in the wheel cylinder was calculated, and the vehicle stability control was realized. A combined simulation platform was set up using softwares Matlab/Simulink and AMESim which was applied to verify the proposed algorithm. The results show that the algorithm has good real-time ability and control effect, can satisfy the request of vehicle stability control.

利用AMESim软件搭建了整车和液压制动系统模型。将基于H∞控制理论的PID控制算法应用于汽车稳定性控制的研究。根据车辆行驶状态的变化调整鲁棒PID控制器的参数，构建以横摆角速度和质心侧偏角为控制目标的汽车稳定性控制算法。进而利用PID控制算法得出制动轮缸压力，实现了整车的稳定性控制。利用Matlab/Simulink和AMESim建立联合仿真平台，对控制算法进行验证。结果表明，该控制算法具有很好的实时性和控制效果，能够满足车辆稳定性控制的要求。

... =1,则根据控制系统鲁棒稳定性定理^[15,16],可以得到在车辆横向运动系统为内部稳定的充要条件为控制系统的最大奇异值小于1,即: ...