机器人在当前生产生活中的应用越来越广泛, 正在代替人发挥着日益重要的作用。特别是一些人类无法到达的地方和可能危及人类生命的特殊场合, 如星球表面、野外考察、水下勘探、防灾救援和反恐等。与轮式、履带式机器人相比, 在崎岖不平的路面, 步行机器人具有更好的地面适应能力和稳定性^{[1, 2, 3]}。四足步行机器人相比两足、六足、八足机器人, 具有承载能力强、稳定性好, 结构简单, 易于控制等显著特点, 成为仿生机器人领域的研究热点^[4]。然而目前四足步行机器人的腿结构均采用刚性设计与连接, 在动态步行中不可避免地会遭受到地面的冲击作用, 频繁或较大的冲击振动不仅会对机器人系统造成重大损伤, 同时也增加了机器人系统的控制难度, 降低了腿机构的能量利用率^[5]。如何提高步行腿机构的缓冲储能性能已经成为国内外广泛关注的问题^{[5, 6, 7]}。

目前, 研究者主要采取在步行机器人的腿机构中加入弹性阻尼元件或采用弹性材料来获得一定的缓冲效果^{[5, 6, 7, 8, 9]}。而部分研究者将目光投向自然界, 以陆地四足动物-犬为生物原型开展运动力学研究, 以获得新的启示^{[10, 11]}。Chi等^[12]研究了犬足垫组织材料的粘弹特性的影响。田为军等^[13]测试分析了在慢走及小跑运动状态下, 犬下肢关节角的变化范围, 以及足与地的作用力特点。钱志辉等^[14]研究了在常速行走、对角小跑以及跳跃步态下, 犬在落地缓冲阶段其足-地接触变化规律及其对缓冲的影响。这些研究工作为四足机器人腿-足结构的设计提供了生物力学参考。但是, 目前对于多种运动步态下犬下肢各主要关节角在触地缓冲阶段的变化规律的报道较少。

本文以德国牧羊犬为研究对象, 测试分析其在正常行走、对角小跑、跳跃三种步态下各关节角在触地缓冲阶段的调整规律, 并分析其对犬下肢缓冲功能的影响, 为具备较佳缓冲功能的四足机器人腿机构的创新设计提供一定的理论依据。

德国牧羊犬动作敏捷轻快, 运动中表现出较好的缓冲特性, 并且性情温良、听从指挥, 因此选择了3条体型正常、体格健硕的德国牧羊犬(来自长春警犬基地)作为研究对象。受试犬的平均年龄为5岁, 平均体质量为33 kg, 平均身高为65 cm, 平均身长为83 cm。受试犬无任何下肢疾病、外伤或手术史。试验前, 在受试犬的解剖学标记点处分别粘贴自制的直径为8 mm的反光球, 每条腿上各6个, 标记位置分别为肩胛骨、肩关节、肘关节、腕关节、掌-指关节和第三个指骨, 如图1所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 运动捕捉标记系统Fig.1 Marker system for motion capture

试验设备采用光学三维动作捕捉系统VICON MX(英国Vicon motion systems公司)来实时获取德国牧羊犬的运动学数据。本次试验共使用了8个红外摄像头, 分别布置于捕捉空间的周围, 以采集犬体表标记点的三维空间运动轨迹, 采集频率设定为200 Hz, 如图2所示。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 三维运动捕捉系统Fig.2 Three dimensional motion capture system

在进行动态测试之前, 受试犬需静止站立于测试空间内以检测是否有反光球被遮挡, 同时获取静止站立时的各关节角角度。对于同一受试犬, 进行一次标定后可采集其在多种运动模式下的运动学数据, 更换受试对象后, 则需要重复该静态标定过程, 再进行相应受试犬的数据采集。之后, 由驯犬员施令, 受试犬分别做常速行走、对角小跑和跳跃三种运动。其中跳跃运动通过使犬从0.5 m的高台上跳下来实现。测试过程中, 对同一只受试犬在同一种运动模式下的运动学数据进行多次采集, 确保其中至少三次数据质量较好。

研究表明, 德国牧羊犬在运动过程中, 其前肢、后肢受到的最大垂直地反力分别占到了体重的63%和37%左右, 由此犬前肢承受地面冲击作用(垂直地面方向)更显著^[13]。因此, 本文侧重分析受试犬的右前腿各关节角在触地缓冲阶段的变化规律与特征。针对每一种运动模式, 分别选择每只犬的三次试验数据进行分析。

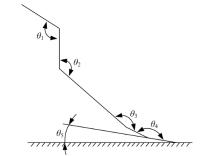
各标记点的空间位移数据利用VICON MX系统处理获得各关节角的角度, 通过Matlab生成角度位移曲线。本文对矢状面内肩关节角(θ ₁)、肘关节角(θ ₂)、腕关节角(θ ₃)、掌-指关节角(θ ₄)、指骨与地面的夹角(θ ₅)的定义如图3所示。本文选择的分析周期为从犬的右前足触地开始到同一足离地为止(触地阶段)。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 关节角度定义示意图Fig.3 Joint angle definitions of GSD fore-lower limb

前期研究表明^[14], 在常速行走、对角小跑、跳跃三种运动步态下, 犬右前足触地时的垂直地反力分别约为其体重的0.72、1.02和1.43倍, 因此地面对下肢的冲击作用持续增强。为分析方便, 本文将犬前足触地阶段视为一个触地周期, 并分为初始触地缓冲和完全触地调整两个阶段。

2.1 肩关节角(θ ₁)

如图4所示, 在三种运动状态下, 犬右前足刚触地时, 犬的肩关节角均达到最大值, 而后关节迅速做屈曲运动进行缓冲适应, 关节角度减小, 此过程约占触地周期的20%~25%, 之后进入触地调整阶段。由表1可知, 肩关节在常速行走、对角小跑和跳跃三种运动状态下的屈曲角位移分别约为22.46° 、33.35° 、17.99° 。相比常速行走, 对角小跑的肩关节屈曲角位移显著增长, 而跳跃状态的角位移偏小, 结合后续分析, 这可能是由于在此次试验中犬的跳跃运动是从高处跳下, 在此过程中犬身体前倾使得肩关节的伸展受到限制, 进而导致其关节角初始值和屈曲幅值较小。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 典型个体肩关节的角位移特征Fig.4 Angular displacement of humeral joint

表1

Table 1

表1(Table 1)

表1 三种运动状态下触地缓冲阶段肩关节角(θ 1)的变化 Table 1 Variations of humeral joint angle (θ 1) in three gait patterns in stance phase 测试 对象 常速行走/(° ) 对角小跑/(° ) 跳跃/(° ) 最大值 最小值 幅值 最大值 最小值 幅值 最大值 最小值 幅值 Sub_1 146.72± 1.09 128.55± 1.61 18.16± 1.38 144.99± 1.91 118.53± 1.04 26.51± 2.26 133.26± 0.91 122.96± 3.2 13.03± 2.3 Sub_2 155.33± 0.82 130.57± 0.69 24.77± 0.13 155.41± 2.5 121.37± 1.48 34.04± 3.99 145.96± 0.49 125.04± 0.59 20.92± 1.08 Sub_3 154.7± 2.06 130.26± 0.16 24.44± 1.91 153.66± 2.4 114.17± 2.34 39.51± 4.25 142.15± 1.81 122.11± 1.98 20.03± 3.78 Mean± Std 152.25± 4.8 129.79± 1.09 22.46± 3.72 151.35± 0.91 118.02± 3.63 33.35± 2.74 143.79± 1.96 123.37± 1.51 17.99± 4.32

表1 三种运动状态下触地缓冲阶段肩关节角(θ 1)的变化 Table 1 Variations of humeral joint angle (θ 1) in three gait patterns in stance phase

2.2 肘关节角(θ ₂)

与肩关节角不同的是, 在常速行走、对角小跑和跳跃三种运动状态下, 犬的右前足指骨接触地面后, 其肘关节角度继续增长,

即并未立即开始屈曲运动进行缓冲, 而是在掌垫接触地面时, 该关节角达到最大值(见图5)。之后, 开始屈曲缓冲, 此阶段分别约占触地周期的12%(常速)、27%(对角小跑、跳跃)。结合表2可知, 在三种运动状态下, 随着垂直地反力的增大, 肘关节的屈曲角位移呈随之增长的变化趋势。触地调整阶段, 由于犬身体重心的前移, 此阶段的肘关节开始做伸张运动, 直到触地周期结束。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 典型个体肘关节的角位移特征Fig.5 Angular displacement of cubital joint

表2

Table 2

表2(Table 2)

表2 三种运动状态下触地缓冲阶段肘关节角(θ 2)的变化 Table 2 Variations of cubital joint angle (θ 2) in three gait patterns in stance phase 测试 对象 常速行走/(° ) 对角小跑/(° ) 跳跃/(° ) 最大值 最小值 幅值 最大值 最小值 幅值 最大值 最小值 幅值 Sub_1 147.79± 0.97 129.81± 3.16 17.98± 3.51 149.65± 3.13 124.67± 1.86 24.98± 1.42 151.15± 0.01 114.33± 2.07 36.82± 2.08 Sub_2 148.98± 0.91 122.26± 0.97 26.72± 0.56 154.06± 0.71 122.97± 0.45 31.09± 1.16 140.45± 0.36 108.01± 0.59 32.45± 0.77 Sub_3 149.3± 1.16 126.54± 3.51 13.76± 2.35 154.94± 4.37 129.73± 0.39 25.2± 4.76 166.68± 2.02 112.81± 3.17 33.87± 5.36 Mean± Std 148.69± 0.8 126.2± 3.79 19.49± 6.61 152.88± 2.83 125.79± 3.52 27.09± 3.47 152.76± 13.19 111.72± 3.3 34.38± 2.23

表2 三种运动状态下触地缓冲阶段肘关节角(θ 2)的变化 Table 2 Variations of cubital joint angle (θ 2) in three gait patterns in stance phase

2.3 腕关节角(θ ₃)

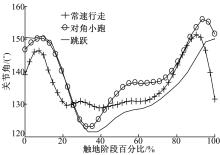
如图6所示, 犬的腕关节在其右前足刚触地时, 关节角度达到触地阶段的最大值, 触地后开始缓慢(相比肩关节和肘关节)做屈伸运动, 此阶段约占触地周期的60%。与肘关节相类似, 在常速行走、对角小跑和跳跃三种运动状态下, 腕关节屈伸角位移也呈现逐渐增大趋势(见表3)。触地调整阶段, 腕关节开始有所伸张, 为前足蹬地进入空中滑翔阶段(swing phase)做准备。

表3

Table 3

表3(Table 3)

表3 三种运动状态下触地缓冲阶段腕关节角(θ 3)的变化 Table 3 Variations of carpal joint angle (θ 3) in three gait patterns in stance phase 测试 对象 常速行走/(° ) 对角小跑/(° ) 跳跃/(° ) 最大值 最小值 幅值 最大值 最小值 幅值 最大值 最小值 幅值 Sub_1 169.23± 2.55 144.81± 1.88 24.42± 1.7 169.77± 0.75 135.24± 2.48 34.99± 2.92 168.58± 0.86 128.91± 2.43 39.67± 3.15 Sub_2 165.17± 0.70 143.46± 0.12 21.71± 0.58 168.75± 0.52 140.48± 0.55 28.27± 1.07 178.01± 0.06 134.01± 0.61 44.04± 0.54 Sub_3 177.4± 1.20 155.48± 0.43 21.92± 1.62 173.87± 0.19 148.42± 0.14 25.49± 0.12 169.18± 0.50 130.65± 0.66 38.53± 1.15 Mean± Std 170.6± 6.23 147.92± 6.58 22.68± 1.51 170.8± 2.71 141.38± 6.64 29.58± 4.88 171.92± 5.28 131.19± 2.59 40.75± 2.91

表3 三种运动状态下触地缓冲阶段腕关节角(θ 3)的变化 Table 3 Variations of carpal joint angle (θ 3) in three gait patterns in stance phase

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 典型个体腕关节的角位移特征Fig.6 Angular displacement of carpal joint

2.4 掌-指关节角(θ ₄)

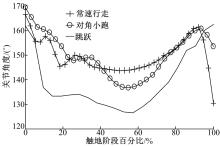
在常速行走、对角小跑、跳跃三种运动状态下, 犬右前足刚触地时, 其掌-指关节角在触地前期均存在一定波动(见图7), 这应该是由于掌垫此时尚未完全触地, 其柔性变形导致的接触状态的变化。由图7及表4可知, 三种运动状态下, 犬的掌指关节屈曲运动持续时间均较长, 约占触地周期的80%, 但三种运动状态下的关节屈曲角位移差别不大。

表4

Table 4

表4(Table 4)

表4 三种运动状态下触地缓冲阶段掌指关节角(θ 4)的变化 Table 4 Variations of metacarpal-phalangeal joint angle (θ 4) in three gait patterns in stance phase 测试 对象 常速行走/(° ) 对角小跑/(° ) 跳跃/(° ) 最大值 最小值 幅值 最大值 最小值 幅值 最大值 最小值 幅值 Sub_1 145.14± 1.34 103.57± 2.93 41.57± 4.23 143.27± 1.33 105.56± 1.31 37.72± 2.35 143.64± 2.79 105.54± 2.34 38.09± 2.25 Sub_2 144.97± 0.04 112.82± 1.26 32.15± 1.3 153.2± 0.61 114.57± 1.35 38.65± 1.95 146.55± 0.56 103.94± 1.09 42.92± 1.65 Sub_3 151.09± 3.03 108.57± 3.85 42.52± 6.88 153.31± 3.18 108.85± 1.37 44.46± 4.55 150.53± 1.25 111.34± 1.9 39.17± 0.64 Mean± Std 147.07± 3.49 108.32± 4.63 38.75± 5.73 149.93± 5.77 109.66± 4.56 40.28± 3.65 146.91± 3.46 106.94± 3.89 40.06± 2.54

表4 三种运动状态下触地缓冲阶段掌指关节角(θ 4)的变化 Table 4 Variations of metacarpal-phalangeal joint angle (θ 4) in three gait patterns in stance phase

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 典型个体掌指关节的角位移特征Fig.7 Angular displacement of metacarpal- phalangeal joint

2.5 指骨与地面夹角(θ ₅)

指骨为犬足部的末端被动环节, 为指行动物的初始触地部位。结合表5的数据统计, 研究发现, 三种运动状态下, 随着地面冲击作用力的增强, 犬指骨触地的初始夹角也逐渐增大, 由常速行走运动的15.79° 增大到跳跃运动时的34.86° 。

表5

Table 5

表5(Table 5)

表5 三种运动状态下的θ 5统计表 Table 5 Variations of initial contact angle of θ 5 between ground and GSD finger 运动状态 常速行走/(° ) 对角小跑/(° ) 跳跃/(° ) Sub_1 17.85± 3.82 26.14± 1.87 31.78± 2.10 Sub_2 13.72± 2.81 20.65± 3.07 37.07± 2.22 Sub_3 15.81± 3.09 21.15± 0.64 35.73± 3.89 Mean± Std 15.79± 2.07 22.65± 3.04 34.86± 2.75

表5 三种运动状态下的θ 5统计表 Table 5 Variations of initial contact angle of θ 5 between ground and GSD finger

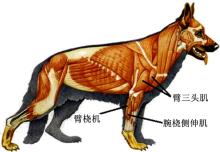
由此, 本文作如下分析:常速行走、对角小跑和跳跃三种运动状态下的犬前肢受到的垂直地反力逐渐显著增大, 为了保护其腿-足系统组织结构不受损伤或将损伤降到最低, 犬前肢各关节在初始触地阶段通过进行屈曲运动来缓解地面的冲击作用。而犬下肢分布着多条强壮的肌肉组, 如臂三头肌、腕桡侧伸肌等(见图8), 关节的屈曲直接导致绕过关节的肌肉组/群做离心运动(肌肉作退让性运动), 因此吸收了部分冲击能量, 降低了冲击作用强度。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 犬下肢肌肉分布示意图Fig.8 Distribution diagram of canine limbs muscle

同时, 综合前肢各个关节屈曲角位移变化可以得出, 随着地反力的增大, 德国牧羊犬右前肢肩关节、肘关节、腕关节的屈曲角位移均随之增长, 但掌-指关节变化不明显, 考虑到跨越关节分布的肌肉的退让性运动, 这表明犬右前肢肩关节、肘关节、腕关节相比掌-指关节在犬前足触地阶段对冲击能量的吸收起着更为重要的作用。

另外, 在三种运动状态下, 从肩关节到掌-指关节, 犬下肢各关节屈曲缓冲阶段占触地周期的比例呈递增趋势; 并且腕关节的实际最大关节角出现在触地阶段前, 肩关节的实际最大关节角恰好出现在刚触地时刻, 而肘关节角的实际最大关节角出现在触地之后(触地周期10%处, 见图5), 说明三个关节发挥屈曲缓冲作用的时刻不同, 腕关节要早于肩关节, 肩关节早于肘关节, 这体现了犬下肢的缓冲是一种多关节的时空协调运动。

在犬足触地缓冲过程中, 相比其他关节, 作为末端关节的掌-指关节屈曲角度(θ ₄)变化较小, 但其指骨与地面的夹角(或触地夹角θ ₅)随着地面冲击力的增加呈现出增大趋势, 由于犬的指骨是犬下肢的末端完全被动环节, 这种适应性调整可能有利于延长足-地作用时间, 进而减小地反力作用强度。

(1)在多种步态下, 犬前肢各关节在初始触地阶段通过进行屈曲运动来缓解地面的冲击作用, 并且其前肢肩关节、肘关节、腕关节相比掌-指关节在犬前足触地阶段对冲击能量的吸收起着更为重要的作用。

(2)犬下肢的缓冲是一种多关节的时空协调运动, 肩关节、肘关节、腕关节发挥屈曲缓冲作用的时刻不同, 腕关节要早于肩关节, 肩关节早于肘关节, 并且从肩关节到掌-指关节, 犬下肢各关节屈曲缓冲阶段占触地周期的比例呈递增趋势。

(3)指骨与地面的夹角随着地面冲击力的增加呈现出增大趋势。