基于多步时延的可重构机械臂并发故障分散容错控制

引用本文

李元春, 周帆, 马天豪, 赵博. 基于多步时延的可重构机械臂并发故障分散容错控制. 2015, 45(6): 1874-1880
LI Yuan-chun, ZHOU Fan, MA Tian-hao, ZHAO Bo. Decentralized fault-tolerant control based on multi-step time delay for reconfigurable manipulator with concurrent failures. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1874-1880 复制到剪切板

Permissions

基于多步时延的可重构机械臂并发故障分散容错控制

李元春¹, 周帆¹, 马天豪¹, 赵博^1,²

1.长春工业大学电气与电子工程学院,长春 130012

2.中国科学院自动化研究所复杂系统管理与控制国家重点实验室,北京 100190

赵博(1987-),男,在站博士后.研究方向:可重构机器人故障诊断与容错控制.E-mail:zhaob09@mails.jlu.edu.cn

作者简介:李元春(1962-),男,教授,博士生导师.研究方向:智能机械与机器人控制.E-mail:liyc@mail.ccut.edu.cn

基金:国家自然科学基金项目(61374051,60974010); 吉林省科技发展计划项目(20150520112JH)

摘要

基于Lyapunov稳定性理论和可重构机械臂的模块化属性,针对非故障系统设计了分散反演神经网络控制器,并采用自适应神经网络系统补偿子系统关联项对系统控制精度的影响。通过引入一阶滤波器将传感器故障转化成伪执行器故障,从而得到增广故障子系统模型,进而采用多步时延技术补偿并发故障,实现容错。两种不同构形的2-DOF可重构机械臂系统的仿真结果表明了所设计分散容错控制方法的有效性。

关键词: 自动控制技术; 可重构机械臂; 分散容错控制; 多步时延; 并发故障

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2015)06-1874-07

Decentralized fault-tolerant control based on multi-step time delay for reconfigurable manipulator with concurrent failures

LI Yuan-chun¹, ZHOU Fan¹, MA Tian-hao¹, ZHAO Bo^1,²

1.College of Electrical and Electronic Engineering, Changchun University of Technology, Changchun, 130012, China

2.State Key Laboratory of Management and Control for Complex Systems, Institute of Automation, Chinese Academy of Sciences, Beijing 100190, China

Abstract

According to Lyapunov stable theory and the modularity of reconfigurable manipulator, a decentralized backstepping neural network controller is designed for the fault free system, and the adaptive neural network system is employed to compensate the reduced control accuracy from the interconnection term. An augmented subsystem is obtained by introducing a filter, which maps the sensor fault into pseudo actuator fault, and then the multi-step time-delay technique is adopted to compensate the concurrent failures and realize the fault-tolerant. Simulations illustrated by two 2-DOF reconfigurable manipulators with different configurations demonstrate the effectiveness of the proposed scheme.

Keyword: automatic control technique; reconfigurable manipulator; decentralized fault-tolerant control; multi-step time-delay; concurrent failure

Show Figures

0 引言

可重构机械臂因其具有高度柔性结构在诸如航空航天、精密装配、核工业等人类无法直接参与的工作任务中有着广泛的应用前景。然而, 长期工作在这些人类无法直接干预的环境中, 其执行器和传感器等部件不可避免地发生故障, 若不能得到及时的处理, 将会造成不可估量的损失, 因此针对其故障诊断和容错问题的研究极为重要。

一些学者针对各类故障问题已经提出了相应的解决方法^{[1, 2, 3, 4]}。肖冰等^[5]通过滑模变结构控制器实现了故障容错和干扰抑制。Brambilla等^[6]设计了次最优二阶滑模控制器并设计了观测器控制律。Henrik等^[7]提出一种包含故障检测、隔离和重构的主动容错控制结构。上述方法只是针对单一故障进行容错, 而在实际复杂的控制系统中, 执行器和传感器故障完全可能同时存在。Jiang等^[8]针对线性系统可能存在的执行器、传感器及元部件故障, 根据不同故障情况选择不同的控制器并修正系统控制命令。Sami等^[9]结合T-S模糊模型, 利用动态输出反馈控制实现对非线性系统执行器故障和传感器故障的容错。陶洪峰等^[10]利用鲁棒容错控制, 保证了整个闭环系统在执行器和传感器多故障并发时的稳定性。这种方法不需要检测和诊断环节, 可以直接对故障进行容错, 但不适用于需要实时控制的机器人系统。

本文考虑了可重构机械臂系统执行器和传感器故障并发的情形, 提出了基于多步时延技术的分散容错控制方法。利用可重构机械臂模块化特点, 在系统正常运行时, 采用分散反演神经网络控制方法对系统进行控制; 当系统发生并发故障时, 将故障作为未知动力学的一部分处理, 利用多步时延技术补偿故障对系统控制性能的影响。该方法不需要对故障进行任何估计。

1 问题描述

存在并发故障子系统i的动力学模型为^[11]:

$\begin{matrix} S_{if} : \{\begin{matrix} \begin{matrix} {\overset{\cdot}{x}}_{i} = A_{i} x_{i} + B_{i} \{f_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) + h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) \\ g_{i} (q_{i}) [u_{i} + f_{ia} (q_{i}, {\overset{\cdot}{q}}_{i}, {\overset{\cdot}{u}}_{i})]\} \end{matrix} \\ y_{i} = C_{i} (x_{i} + f_{is}) \end{matrix} (1) \end{matrix}$

式中:x_i= $\begin{matrix} [x_{i 1}, x_{i 2}]^{T} \end{matrix}$ = $\begin{matrix} [q_{i}, {\overset{\cdot}{q}}_{i}]^{T} \end{matrix}$ , (i=1, 2, …, n)为子系统S_i的状态变量; y_i为子系统S_if的输出; f_ia $\begin{matrix} (q_{i}, {\overset{\cdot}{q}}_{i}, {\overset{\cdot}{u}}_{i}) \end{matrix}$ 为执行器故障函数; f_is= $\begin{matrix} {[\begin{matrix} f_{is 1} & f_{is 2} \end{matrix}]}^{T} \end{matrix}$ 为子系统传感器故障函数矩阵, 且满足‖ f_is‖ ≤ ρ _it, 其中ρ _it是已知连续函数。h_i(q, $\begin{matrix} \overset{\cdot}{q} \end{matrix}$ , $\begin{matrix} \overset{\cdot \cdot}{q} \end{matrix}$ )=- $\begin{matrix} M_{i}^{- 1} \end{matrix}$ (q_i)Z_i(q, $\begin{matrix} \overset{\cdot}{q} \end{matrix}$ , $\begin{matrix} \overset{\cdot \cdot}{q} \end{matrix}$ );

A_i= $\begin{matrix} [\begin{matrix} 0 & 1 \\ 0 & 0 \end{matrix}] \end{matrix}$ ; B_i= $\begin{matrix} [\begin{matrix} 0 \\ 1 \end{matrix}] \end{matrix}$ ; C_i= $\begin{matrix} [\begin{matrix} 1 & 0 \\ 0 & 1 \end{matrix}] \end{matrix}$ ;

f_i(q_i, $\begin{matrix} {\overset{\cdot}{q}}_{i} \end{matrix}$ )= $\begin{matrix} M_{i}^{- 1} \end{matrix}$ (q_i)[-C_i(q_i, $\begin{matrix} {\overset{\cdot}{q}}_{i} \end{matrix}$ ) $\begin{matrix} {\overset{\cdot}{q}}_{i} \end{matrix}$ -G_i(q_i)];

g_i(q_i)= $\begin{matrix} M_{i}^{- 1} \end{matrix}$ (q_i);

引入一阶滤波器z_i将传感器故障转化为伪执行器故障^[12]:

$\begin{matrix} {\overset{\cdot}{z}}_{i} = - A_{ia} z_{i} + B_{ia} y_{i} (2) \end{matrix}$

式中:z_i=[z_i₁z_i₂]^T; y_i为子系统i的输出信号。

令A_ia=B_ia=diag(1, 1), 则将式(1)中输出方程代入式(2)中得:

$\begin{matrix} {\overset{\cdot}{z}}_{i} = - z_{i} + x_{i} + f_{is} (3) \end{matrix}$

令 $\begin{matrix} {\bar{x}}_{i} \end{matrix}$ = $\begin{matrix} {[x_{i 1}, x_{i 2}, x_{i 3}, x_{i 4}]}^{T} \end{matrix}$ = $\begin{matrix} {[q_{i}, {\overset{\cdot}{q}}_{i}, z_{i 1}, z_{i 2}]}^{T} \end{matrix}$ , 将式(1)和式(3)整合为增广子系统, 则故障系统可描述为:

$\begin{matrix} {\bar{S}}_{i} : \{\begin{matrix} {\overset{\cdot \cdot}{q}}_{i} = f_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) + h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) + \\ g_{i} (q_{i}) [u_{i} + f_{ia} (q_{i}, {\overset{\cdot}{q}}_{i}, {\overset{\cdot}{u}}_{i})] \\ {\overset{\cdot}{Z}}_{i 1} = q_{i} - Z_{i 1} + f_{is 1} \\ {\overset{\cdot}{Z}}_{i 2} = {\overset{\cdot}{q}}_{i} - Z_{i 2} + f_{is 2} \end{matrix} (4) \end{matrix}$

本文的控制目标是:针对并发故障子系统模型(式(4))设计基于多步时延技术的分散容错控制律, 使可重构机械臂系统发生故障时, 关节位置仍可跟踪期望轨迹。

2 分散控制器设计

假设1 期望轨迹 $\begin{matrix} q_{i}^{d} \end{matrix}$ , $\begin{matrix} {\overset{\cdot}{q}}_{i}^{d} \end{matrix}$ , $\begin{matrix} {\overset{\cdot \cdot}{q}}_{i}^{d} \end{matrix}$ 有界。

定义子系统i的位置跟踪误差为:

$\begin{matrix} \begin{matrix} e_{i 1} = x_{i 1} - x_{i 1}^{d} (5) \\ 则 : {\overset{\cdot}{e}}_{i 1}^{d} = {\overset{\cdot}{x}}_{i 1} - {\overset{\cdot}{x}}_{i 1}^{d} = x_{i 2} - {\overset{\cdot}{x}}_{i 1}^{d} (6) \end{matrix} \end{matrix}$

定义速度跟踪误差为:

$\begin{matrix} e_{i 2} = x_{i 2} - x_{i 2}^{d} (7) \end{matrix}$

则其导数为:

$\begin{matrix} {\overset{\cdot}{e}}_{i 2} = f_{i} (q_{i}, {\overset{\cdot}{q}}_{i}) + g_{i} (q_{i}) u_{i} + h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) - {\overset{\cdot}{x}}_{i 2}^{d} (8) \end{matrix}$

定义虚拟控制律为:

$\begin{matrix} x_{i 2}^{d} = {\overset{\cdot}{x}}_{i 1}^{d} - k_{i 1} e_{i 1} (9) \end{matrix}$

式中:k_i₁> 0。

引入Lyapunov函数:

$\begin{matrix} V_{i 1} = e_{i 1}^{2} / 2 (10) \end{matrix}$

则其导数为:

$\begin{matrix} {\overset{\cdot}{V}}_{i 1} = e_{i 1} e_{i 2} - k_{i 1} e_{i 1} (11) \end{matrix}$

下面采用RBF神经网络 $\begin{matrix} {\hat{f}}_{i} \end{matrix} \begin{matrix} (q_{i}, {\overset{\cdot}{q}}_{i}) \end{matrix}$ 和 $\begin{matrix} {\hat{g}}_{i} \end{matrix} \begin{matrix} (q_{i}) \end{matrix}$ 分别对系统的非线性项f_i $\begin{matrix} (q_{i}, {\overset{\cdot}{q}}_{i}) \end{matrix}$ 和g_i $\begin{matrix} (q_{i}) \end{matrix}$ 进行估计, 理想神经网络逼近如下:

$\begin{matrix} \begin{matrix} f_{i} (q_{i}, {\overset{\cdot}{q}}_{i}, W_{if}) = {W^{T}}_{if} Φ_{if} (q_{i}, {\overset{\cdot}{q}}_{i}) + ε_{if} (12) \\ g_{i} (q_{i}, W_{ig}) = {W^{T}}_{ig} Φ_{ig} (q_{i}) + ε_{ig} (13) \end{matrix} \end{matrix}$

式中:W_if、W_ig为理想神经网络权值; Φ (· )为神经网络基函数; ε _if、ε _ig为神经网络估计误差。

定义 $\begin{matrix} {\hat{W}}_{if} \end{matrix}$ 和 $\begin{matrix} {\hat{W}}_{ig} \end{matrix}$ 分别为W_if和W_ig的估计值; $\begin{matrix} {\hat{f}}_{i} \end{matrix}$ (q_i, $\begin{matrix} {\overset{\cdot}{q}}_{i} \end{matrix}$ , $\begin{matrix} {\hat{W}}_{if} \end{matrix}$ )和 $\begin{matrix} {\hat{g}}_{i} \end{matrix}$ (q_i, $\begin{matrix} {\hat{W}}_{ig} \end{matrix}$ )分别为f_i(q_i, $\begin{matrix} {\overset{\cdot}{q}}_{i} \end{matrix}$ , W_if)和g_i(q_i, W_ig)的估计值, 则:

$\begin{matrix} \begin{matrix} {\hat{f}}_{i} (q_{i}, {\overset{\cdot}{q}}_{i}, {\hat{W}}_{if}^{T}) = {\hat{W}}^{T}_{if} {\hat{Φ}}_{if} (q_{i}, {\overset{\cdot}{q}}_{i}) (14) \\ {\hat{g}}_{i} (q_{i}, {\hat{W}}^{T}_{ig}) = {\hat{W}}^{T}_{ig} {\hat{Φ}}_{ig} (q_{i}) (15) \end{matrix} \end{matrix}$

定义 $\begin{matrix} {\tilde{W}}_{if} \end{matrix}$ =W_if- $\begin{matrix} {\hat{W}}_{if} \end{matrix}$ 和 $\begin{matrix} {\tilde{W}}_{ig} \end{matrix}$ =W_ig- $\begin{matrix} {\hat{W}}_{ig} \end{matrix}$ 为权值估计误差, 则:

$\begin{matrix} \begin{matrix} f_{i} (q_{i}, {\overset{\cdot}{q}}_{i}, W_{if}) - {\hat{f}}_{i} (q_{i}, {\overset{\cdot}{q}}_{i}, {\hat{W}}_{if}) = \\ {\tilde{W}}^{T}_{if} {\hat{Φ}}_{if} (q_{i}, {\overset{\cdot}{q}}_{i}) + {W^{T}}_{if} {\dot{Φ}}_{if} (q_{i}, {\overset{\cdot}{q}}_{i}) + ε_{if} (16) \\ g_{i} (q_{i}, W_{ig}) - {\hat{g}}_{i} (q_{i}, {\hat{W}}_{ig}) = \\ {\tilde{W}}^{T}_{ig} {\hat{Φ}}_{ig} (q_{i}) + {W^{T}}_{ig} {\dot{Φ}}_{ig} (q_{i}) + ε_{ig} (17) \end{matrix} \end{matrix}$

式中:RBF神经网络基函数输出误差 $\begin{matrix} \dot{Φ} \end{matrix}$ (· )为:

$\begin{matrix} \begin{matrix} {\dot{Φ}}_{if} (q_{i}, {\overset{\cdot}{q}}_{i}) = Φ_{if} (q_{i}, {\overset{\cdot}{q}}_{i}) - {\hat{Φ}}_{if} (q_{i}, {\overset{\cdot}{q}}_{i}) (18) \\ {\dot{Φ}}_{ig} (q_{i}) = Φ_{ig} (q_{i}) - {\hat{Φ}}_{ig} (q_{i}) (19) \end{matrix} \end{matrix}$

假设2 交联项h_i $\begin{matrix} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q}) \end{matrix}$ 有界且满足^[13]:

$\begin{matrix} |h_{i} (q, \overset{\cdot}{q}, \overset{\cdot \cdot}{q})| \leq \overset{n}{\sum_{j = 1}} d_{ij} E_{j} (20) \end{matrix}$

式中:d_ij≥ 0; E_j=1+ $\begin{matrix} |e_{j}| \end{matrix}$ + $\begin{matrix} {|e_{j}|}^{2} \end{matrix}$ 。

并定义p_i $\begin{matrix} (|e_{i 2}|) \end{matrix}$ =n $\begin{matrix} \max_{ij} \end{matrix} \begin{matrix} \{d_{ij}\} \end{matrix}$ E_i。

同理, 采用神经网络系统 $\begin{matrix} {\hat{p}}_{i} \end{matrix}$ ( $\begin{matrix} |e_{i 2}| \end{matrix}$ , $\begin{matrix} {\hat{W}}_{ip} \end{matrix}$ )补偿关联项的影响, $\begin{matrix} {\hat{p}}_{i} \end{matrix}$ ( $\begin{matrix} |e_{i 2}| \end{matrix}$ , $\begin{matrix} {\hat{W}}_{ip} \end{matrix}$ )可表示为:

$\begin{matrix} {\hat{p}}_{i} (|e_{i 2}|, {\hat{W}}_{ip}) = {\hat{W}}^{T}_{ip} {\hat{Φ}}^{T}_{ip} (|e_{i 2}|) (21) \end{matrix}$

式中: $\begin{matrix} {\hat{W}}_{ip} \end{matrix}$ 为W_ip的估计值。

权值估计误差为 $\begin{matrix} {\tilde{W}}_{ip} \end{matrix}$ =W_ip- $\begin{matrix} {\hat{W}}_{ip} \end{matrix}$ 。

定义最小估计误差为:

$\begin{matrix} \begin{matrix} ω_{i 1} = {W^{T}}_{if} {\dot{Φ}}_{if} (q_{i}, {\overset{\cdot}{q}}_{i}) + {W^{T}}_{ig} {\dot{Φ}}_{ig} (q_{i}) u_{i} + ε_{if} + ε_{ig} u_{i} (22) \\ ω_{i 2} = p_{i} |e_{i 2}| - {\hat{W}}^{T}_{ip} {\hat{Φ}}_{ip} (|e_{i 2}|) (23) \\ ω_{i} = |ω_{i 1}| + |ω_{i 2}| (24) \end{matrix} \end{matrix}$

设计分散反演神经网络控制律为:

$\begin{matrix} \begin{matrix} u_{id} = - \frac{1}{{\hat{g}}_{i} (q_{i}, {\hat{W}}_{ig})} [\hat{f} (q_{i}, {\overset{\cdot}{q}}_{i}, {\hat{W}}_{if}) + {\overset{\cdot}{x}}_{i 2}^{d} + e_{i 1} + \\ k_{i 2} e_{i 2} + sgn (e_{i 2}) \hat{p} (|e_{i 2}, {\hat{W}}_{ip}|)] (25) \end{matrix} \end{matrix}$

其中自适应更新律为:

$\begin{matrix} \begin{matrix} {\overset{\cdot}{\hat{W}}}_{if} = η_{if} |e_{i 2}| {\hat{Φ}}_{if} (q_{i}, {\overset{\cdot}{q}}_{i}) (26) \\ {\overset{\cdot}{\hat{W}}}_{ig} = η_{ig} |e_{i 2}| {\hat{Φ}}_{ig} (q_{i}) u_{i} (27) \\ {\overset{\cdot}{\hat{W}}}_{ip} = η_{ip} |e_{i 2}| {\hat{Φ}}_{ip} (|e_{i 2}|) (28) \end{matrix} \end{matrix}$

式中:η _if、η _ig、η _ip均为正常数。

定理1 考虑系统正常运行时的可重构机械臂子系统动力学模型(式(2))、假设1和假设2, 设计分散反演神经网络控制律(式(25)), 自适应更新律(式(26)~(28)), 则可保证闭环系统稳定, 且轨迹跟踪误差最终一致有界。

证明选择Lyapunov函数:

$\begin{matrix} \begin{matrix} V = \overset{n}{\sum_{i = 1}} V_{i} = \\ \overset{n}{\sum_{i = 1}} (\frac{e_{i 1}^{2}}{2} + \frac{e_{i 2}^{2}}{2} + \frac{1}{2 η_{ip}} {\tilde{W}}^{T}_{ip} {\tilde{W}}_{ip} + \\ \frac{1}{2 η_{if}} {\tilde{W}}^{T}_{if} {\tilde{W}}_{if} + \frac{1}{2 η_{ig}} {\tilde{W}}^{T}_{ig} {\tilde{W}}_{ig}) (29) \end{matrix} \end{matrix}$

对式(29)求导得:

$\begin{matrix} \begin{matrix} \overset{n}{\sum_{i = 1}} {\overset{\cdot}{V}}_{i} = \overset{n}{\sum_{i = 1}} (e_{i 1} {\overset{\cdot}{e}}_{i 1} + e_{i 2} {\overset{\cdot}{e}}_{12} + \frac{1}{η_{ip}} {\tilde{W}}^{T}_{ip} {\overset{\cdot}{\hat{W}}}_{ip} + \\ \frac{1}{η_{if}} {\tilde{W}}^{T}_{if} {\overset{\cdot}{\hat{W}}}_{if} + \frac{1}{η_{ig}} {\tilde{W}}^{T}_{ig} {\overset{\cdot}{\hat{W}}}_{ig}) (30) \end{matrix} \end{matrix}$

将式(25)代入式(30), 并考虑式(22)(27)(28), 根据假设2可知:

$\begin{matrix} \begin{matrix} \overset{n}{\sum_{i = 1}} {\overset{\cdot}{V}}_{i} \leq \overset{n}{\sum_{i = 1}} (- k_{i 1} e_{i 1}^{2} - k_{i 2} e_{12}^{2} + e_{i 2} ω_{i 1} - \\ |e_{i 2}| {\hat{W}}^{T}_{ip} {\hat{Φ}}_{ip} (|e_{i 2}|) - \frac{1}{η_{ip}} {\tilde{W}}^{T}_{ip} {\overset{\cdot}{\hat{W}}}_{ip}) + \\ \max_{i, j} \{d_{ij}\} \overset{n}{\sum_{i = 1}} |e_{i 2}| \overset{n}{\sum_{i = 1}} E_{j} (31) \end{matrix} \end{matrix}$

注意到 $\begin{matrix} |e_{i 2}| \end{matrix}$ ≤ $\begin{matrix} |e_{j 2}| \end{matrix}$ ⇔ E_i≤ E_j, 应用Chebyshev不等式可得:

$\begin{matrix} \overset{n}{\sum_{i = 1}} |e_{i 2}| \overset{n}{\sum_{i = 1}} E_{j} \leq n \overset{n}{\sum_{i = 1}} ‖ e_{i 2} ‖ E_{i} (32) \end{matrix}$

联立式(21)(32), 则式(31)可化为:

$\begin{matrix} \begin{matrix} \overset{n}{\sum_{i = 1}} {\overset{\cdot}{V}}_{i} \leq \overset{n}{\sum_{i = 1}} (- k_{i 1} e_{i 1}^{2} - k_{i 2} e_{12}^{2} + e_{i 2} ω_{i 1} + |e_{i 2}| ω_{i 2} + \\ {\tilde{W}}^{T}_{ip} [|e_{i 2}| {\hat{Φ}}_{ip} (|e_{i 2}|)] - \frac{1}{η_{ip}} {\hat{W}}_{ip}) (33) \end{matrix} \end{matrix}$

将式(24)(28)代入式(33)中, 则有:

$\begin{matrix} \begin{matrix} \overset{n}{\sum_{i = 1}} {\overset{\cdot}{V}}_{i} \leq \overset{n}{\sum_{i = 1}} (- k_{i 1} e_{i 1}^{2} - k_{i 2} e_{i 2}^{2} + |e_{2}| ω_{i}) = \\ \overset{n}{\sum_{i = 1}} (- k_{i 1} e_{i 1}^{2} - |e_{i 2}| (k_{i 2} |e_{i 2}| + ω_{i})) (34) \end{matrix} \end{matrix}$

因此, 在紧集(见式(35))之外, $\begin{matrix} \overset{\cdot}{V} \end{matrix}$ 是负定的。根据Lyapunov稳定性理论, 闭环系统是渐近稳定的。

$\begin{matrix} Ω_{e} = \{e_{i 2} : 0 \leq |e_{i 2}| \leq ω_{i} / k_{i 2}\} (35) \end{matrix}$

3 多步时延容错控制器设计

(1)考虑系统只有执行器发生故障时, 由式(4)可得其故障模型为:

$\begin{matrix} \begin{matrix} M_{i} {\overset{\cdot \cdot}{q}}_{i} + C_{i} {\overset{\cdot}{q}}_{i} + G_{i} + H_{i} = u_{i 1} + f_{ia} (36) \end{matrix} \end{matrix}$

取：

$v_{i 1} (t) = - f_{ia} - H_{i} (37)$

则有：

$M_{i} {\overset{\cdot \cdot}{q}}_{i} = - C_{i} {\overset{\cdot}{q}}_{i} - G_{i} + v_{i 1} (t) + u_{i 1} (38)$

选取控制率：

$u_{i 1} = u_{id} - v_{i 1} (t) (39)$

利用时延技术, 采用v_i₁ $\begin{matrix} (t) \end{matrix}$ 的估计值:

$\begin{matrix} \begin{matrix} {\hat{v}}_{i 1} (t) = v_{i 1} (t - T) = \\ M_{i} {\overset{\cdot \cdot}{q}}_{i} (t - T) + C_{i} {\overset{\cdot}{q}}_{i} (t - T) + \\ G_{i} - u_{i 1} (t - T) (40) \end{matrix} \end{matrix}$

替代式(39)中的v_i₁ $\begin{matrix} (t) \end{matrix}$ , 则得到第一步时延控制律为:

$\begin{matrix} \begin{matrix} u_{i 1} (t) = u_{i 1} (t - T) - M_{i} {\overset{\cdot \cdot}{q}}_{i} (t - T) - \\ C_{i} {\overset{\cdot}{q}}_{i} (t - T) - G_{i} + u_{id} (41) \end{matrix} \end{matrix}$

定理2 当系统发生执行器故障时, 对于可重构机械臂子系统动力学模型(式(1))和式(36), 若选取T足够小, 使得:

$\begin{matrix} ‖ {\overset{\cdot}{q}}_{i} (t) - {\overset{\cdot}{q}}_{i} (t - T) ‖ ≪ 1 (42) \end{matrix}$

则由式(1)(36)(42)构成的闭环系统的稳定条件需满足 $\begin{matrix} M_{i}^{- 1} \end{matrix}$ β _i₁M_i非奇异, 且有如下不等式成立:

$\begin{matrix} ‖ I - M_{i}^{- 1} β_{i 1} M_{i} ‖ < 1 (43) \end{matrix}$

式中:β _i₁=(u_i₁-f_ia)/u_i₁, 证明过程见文献[14]。

(2)考虑系统发生执行器和位置传感器故障时, 由式(4)可得其故障模型为:

$\begin{matrix} \begin{matrix} M_{i} {\overset{\dots}{Z}}_{i 1} + (M_{i} + C_{i}) {\overset{\cdot \cdot}{Z}}_{i 1} + C_{i} {\overset{\cdot}{Z}}_{i 1} + G_{i} + H_{i} = \\ u_{i 2} + M_{i} {\overset{\cdot}{f}}_{is 1} + C_{i} {\overset{\cdot \cdot}{f}}_{is 1} (44) \end{matrix} \end{matrix}$

取：

$v_{i 2} (t) = M_{i} {\overset{\cdot}{f}}_{is 1} + C_{i} {\overset{\cdot \cdot}{f}}_{is 1} - H_{i} (45)$

则有：

$M_{i} {\overset{\dots}{Z}}_{i 1} = - (M_{i} + C_{i}) {\overset{\cdot \cdot}{Z}}_{i 1} - C_{i} {\overset{\cdot}{Z}}_{i 1} - G_{i} + v_{i} (t) + u_{i 2} (46)$

选取控制率：

$u_{i 2} = u_{i 1} - v_{i 2} (t) (47)$

利用时延技术, 采用v_i₂ $\begin{matrix} (t) \end{matrix}$ 的估计值

$\begin{matrix} \begin{matrix} {\hat{v}}_{i 2} (t) = v_{i 2} (t - T) = \\ M_{i} {\overset{\dots}{Z}}_{i 1} (t - T) + (M_{i} + C_{i}) {\overset{\cdot \cdot}{Z}}_{i 1} (t - T) + \\ C_{i} {\overset{\cdot}{Z}}_{i 1} (t - T) + G_{i} - u_{i 2} (t - T) (48) \end{matrix} \end{matrix}$

替代式(47)中的v_i₂ $\begin{matrix} (t) \end{matrix}$ , 则得到控制律为:

$\begin{matrix} \begin{matrix} u_{i 2} (t) = u_{i 2} (t - T) - M_{i} {\overset{\dots}{Z}}_{i 1} (t - T) - G_{i} + u_{i 1} - \\ (M_{i} + C_{i}) {\overset{\cdot \cdot}{Z}}_{i 1} (t - T) - C_{i} {\overset{\cdot}{Z}}_{i 1} (t - T) (49) \end{matrix} \end{matrix}$

定理3 当系统发生执行器与位置传感器故障时, 对于可重构机械臂子系统动力学模型(式(1))和式(44), 若选取T足够小, 使得:

$\begin{matrix} \{\begin{matrix} ‖ {\overset{\cdot}{Z}}_{i 1} (t) - {\overset{\cdot}{Z}}_{i 1} (t - T) ‖ ≪ 1 \\ ‖ {\overset{\cdot \cdot}{Z}}_{i 1} (t) - {\overset{\cdot \cdot}{Z}}_{i 1} (t - T) ‖ ≪ 1 \end{matrix} (50) \end{matrix}$

则由式(1)(44)(50)构成的闭环系统的稳定条件需满足 $\begin{matrix} M_{i}^{- 1} \end{matrix}$ β _i₂M_i非奇异, 且有如下不等式成立:

$\begin{matrix} ‖ I - M_{i}^{- 1} β_{i 2} M_{i} ‖ < 1 (51) \end{matrix}$

式中:β _i₂=(u_i₂-f_is₁)/u_i₂。

证明考虑子系统模型

${\overset{\dots}{Z}}_{i 1} (t) = M_{i}^{- 1} [- (M_{i} + C_{i}) {\overset{\cdot \cdot}{Z}}_{i 1} - C_{i} {\overset{\cdot}{Z}}_{i 1} - G_{i}] + M_{i}^{- 1} β_{i 2} u_{i 2} (52)$

相应地有：

$\begin{matrix} \begin{matrix} M_{i}^{- 1} β_{i 2} u_{i 2} (t - T) = \\ {\overset{\dots}{Z}}_{i 1} (t - T) + M_{i}^{- 1} C_{i} {\overset{\cdot}{Z}}_{i 1} (t - T) - \\ (I + M_{i}^{- 1} C_{i}) {\overset{\cdot \cdot}{Z}}_{i 1} (t - T) - M_{i}^{- 1} G_{i} (53) \end{matrix} \end{matrix}$

将式(49)(53)代入式(52), 并结合式(50)得:

$\begin{matrix} \begin{matrix} {\overset{\dots}{Z}}_{i 1} - {\overset{\dots}{Z}}_{i 1} (t - T) = - M_{i}^{- 1} β_{i 2} M_{i} {\overset{\dots}{Z}}_{i 1} (t - T) - \\ M_{i}^{- 1} β_{i 2} (M_{i} + C_{i}) β_{i 2} {\overset{\cdot \cdot}{Z}}_{i 1} (t - T) - \\ M_{i}^{- 1} β_{i 2} C_{i} {\overset{\cdot}{Z}}_{i 1} (t - T) - M_{i}^{- 1} β_{i 2} G_{i} + M_{i}^{- 1} β_{i 2} u_{i 1} (54) \end{matrix} \end{matrix}$

根据定理2, 若满足条件(式(51)), 则有 $\begin{matrix} {\overset{\dots}{Z}}_{i 1} \end{matrix} \begin{matrix} (t - T) \end{matrix}$ → $\begin{matrix} {\overset{\dots}{Z}}_{i 1} \end{matrix} \begin{matrix} (t) \end{matrix}$ , 因此能够得到:

$\begin{matrix} \begin{matrix} 0 \approx {\overset{\dots}{Z}}_{i 1} (t) - {\overset{\dots}{Z}}_{i 1} (t - T) = \\ - {M_{i}}^{- 1} β'_{i} [- u_{i 1} + G_{i} + M_{i} {\overset{\dots}{Z}}_{i 1} (t - T) + \\ (M_{i} + C_{i}) {\overset{\cdot \cdot}{Z}}_{i 1} (t - T) + C_{i} {\overset{\cdot}{Z}}_{i 1} (t - T)] (55) \end{matrix} \end{matrix}$

式中: $\begin{matrix} {\overset{\dots}{Z}}_{i 1} \end{matrix} \begin{matrix} (t - T) \end{matrix}$ → $\begin{matrix} {\overset{\dots}{Z}}_{i 1} \end{matrix} \begin{matrix} (t) \end{matrix}$ ; $\begin{matrix} {\overset{\cdot \cdot}{Z}}_{i 1} \end{matrix} \begin{matrix} (t - T) \end{matrix}$ → $\begin{matrix} {\overset{\cdot \cdot}{Z}}_{i 1} \end{matrix} \begin{matrix} (t) \end{matrix}$ ; $\begin{matrix} {\overset{\cdot}{Z}}_{i 1} \end{matrix} \begin{matrix} (t - T) \end{matrix}$ → $\begin{matrix} {\overset{\cdot}{Z}}_{i 1} \end{matrix} \begin{matrix} (t) \end{matrix}$ 。

则式(55)可写成:

$\begin{matrix} G_{i} + M_{i} {\overset{\dots}{Z}}_{i 1} (t) + (M_{i} + C_{i}) {\overset{\cdot \cdot}{Z}}_{i 1} (t) + C_{i} {\overset{\cdot}{Z}}_{i 1} (t) = u_{i 1} (56) \end{matrix}$

由此, 定理2证毕。

(3)当系统发生执行器、位置传感器和速度传感器故障时, 由式(4)可得其故障模型为:

$\begin{matrix} \begin{matrix} M_{i} {\overset{\cdot \cdot}{Z}}_{i 2} + (M_{i} + C_{i}) {\overset{\cdot}{Z}}_{i 2} + C_{i} Z_{i 2} + G_{i} + H_{i} = \\ u_{i 3} + M_{i} {\overset{\cdot}{f}}_{is 2} + C_{i} f_{is 2} (57) \end{matrix} \end{matrix}$

取：

$v_{i 3} (t) = M_{i} {\overset{\cdot}{f}}_{is 2} + C_{i} f_{is 2} - H_{i} (58)$

则有：

$M_{i} {\overset{\cdot \cdot}{Z}}_{i 2} = - (M_{i} + C_{i}) {\overset{\cdot}{Z}}_{i 2} - C_{i} Z_{i 2} - G_{i} + v_{i} (t) + u_{i 2} (59)$

选取控制率：

$u_{i 3} = u_{i 2} - v_{i 3} (t) (60)$

利用时延技术, 采用v_i₃ $\begin{matrix} (t) \end{matrix}$ 的估计值:

$\begin{matrix} \begin{matrix} {\hat{v}}_{i 3} (t) = v_{i} (t - T) = \\ M_{i} {\overset{\cdot \cdot}{Z}}_{i 2} (t - T) + (M_{i} + C_{i}) {\overset{\cdot}{Z}}_{i 2} (t - T) + \\ C_{i} {\overset{\cdot}{Z}}_{i 2} (t - T) + G_{i} - u_{i 2} (t - T) (61) \end{matrix} \end{matrix}$

用式(61)替代式(60)中的v_i₃ $\begin{matrix} (t) \end{matrix}$ , 则得到控制律:

$\begin{matrix} \begin{matrix} u_{i 3} (t) = u_{i 3} (t - T) - M_{i} {\overset{\cdot \cdot}{Z}}_{i 2} (t - T) - G_{i} + u_{i 2} - \\ (M_{i} + C_{i}) {\overset{\cdot}{Z}}_{i 2} (t - T) - C_{i} Z_{i 2} (t - T) (62) \end{matrix} \end{matrix}$

定理4 当系统发生执行器、位置传感器和速度传感器故障时, 对于可重构机械臂子系统动力学模型(式(1))和式(58), 如果选取T足够小, 使得:

$\begin{matrix} ‖ {\overset{\cdot}{Z}}_{i 2} (t) - {\overset{\cdot}{Z}}_{i 2} (t - T) ‖ ≪ 1 (63) \end{matrix}$

则由式(1)(58)(64)构成的闭环系统的稳定条件需满足 $\begin{matrix} M_{i}^{- 1} \end{matrix}$ β _i₃M_i非奇异, 且如下不等式成立:

$\begin{matrix} ‖ I - M_{i}^{- 1} β_{i 3} M_{i} ‖ < 1 (64) \end{matrix}$

式中:β _i₃=(u_i₃-f_is₂)/u_i₃。

通过类似步骤(2)的证明, 可证明定理4成立。

由于式(62)所示的容错控制律既考虑了执行器故障, 又考虑了两种传感器故障, 因此其可应用于这3种故障同时发生的情形, 也可应用于其中几种故障并发的情形, 只需定理2~4中所给各不等式成立, 则可保证故障并发时闭环系统渐近稳定。

4 数值仿真

采用文献[14]中图1所示两种构形及相同的模型进行仿真。仿真中初始位置设置为q_i $\begin{matrix} (0) \end{matrix}$ =q₂ $\begin{matrix} (0) \end{matrix}$ =1, 初始速度设置为 $\begin{matrix} {\overset{\cdot}{q}}_{i} \end{matrix} \begin{matrix} (0) \end{matrix}$ = $\begin{matrix} {\overset{\cdot}{q}}_{2} \end{matrix} \begin{matrix} (0) \end{matrix}$ =0。控制器参数和自适应增益参数分别为k_i₁=10; k_i₂=30; η _if=η _ig=0.002; η _ip=500; f=0.01。

	Figure Option View Download New Window
	图1 构形a轨迹跟踪曲线Fig.1 Trajectories tracking curves of configuration a

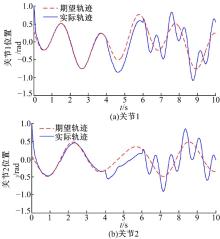
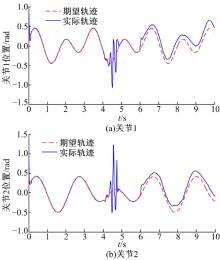
图1为构形a无故障时采用式(25)的分散控制律得到的关节跟踪轨迹曲线, 从图中可看出此控制律有效。图2为针对构形a的关节1在t=4 s时加入位置传感器故障; 关节2在t=6 s时加入执行器故障, 仍采用理想控制律(式(25))的仿真结果。从结果中可以看到, 当故障发生时, 关节轨迹已明显偏离期望轨迹。

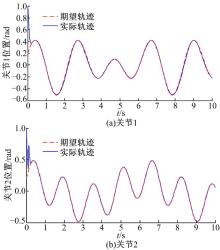
	Figure Option View Download New Window
	图2 构形a故障时轨迹跟踪曲线Fig.2 Trajectories tracking curves of configuration a with concurrent failures

采用分散容错控制律(式(62)), 并修改控制器参数为k_i₁=25, k_i₂=40。图3为系统在故障后的容错控制轨迹跟踪曲线, 表明所设计的分散容错控制方法有效。

	Figure Option View Download New Window
	图3 构形a故障时容错控制轨迹跟踪曲线Fig.3 Fault-tolerant control trajectories tracking curves of configuration a with concurrent failures

针对构形b进行类似的仿真, 结果如图4~图6所示。

	Figure Option View Download New Window
	图4 构形b轨迹跟踪曲线Fig.4 Trajectories tracking curves of configuration b

	Figure Option View Download New Window
	图5 构形b故障时轨迹跟踪曲线Fig.5 Trajectories tracking curves of configuration b with concurrent failures

	Figure Option View Download New Window
	图6 构形b故障时容错控制轨迹跟踪曲线Fig.6 Fault-tolerant control trajectories tracking curves of configuration b with concurrent failures

关节1在t=4 s加入速度传感器故障; 关节2在t=6 s时加入执行器故障。从图4~图6的仿真中可以得到与构形a仿真相同的结论。相比于文献[11]所提方法, 本文方法不需要对故障进行实时诊断和估计。另外与文献[14]相比, 本文所设计的基于多步时延技术的分散容错控制方法不仅可以解决单一执行器故障的情况, 还可以解决执行器和传感器故障并发的情况。

5 结束语

针对可重构机械臂系统中执行器和传感器故障并发的情形, 提出了一种基于多步时延技术的分散容错控制方法。设计了系统正常运行时采用的分散反演神经网络控制器。当系统发生并发故障时, 按照系统阶次逐级进行时延容错处理, 补偿多种故障对控制性能的影响, 不需要对故障进行在线诊断及辨识。通过对不同构形的可重构机械臂系统的仿真结果表明所设计的分散容错控制方法有效。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Xiang Zheng-rong, Wang Rong-hao, Chen Qing-wei. Fault tolerant control of switched nonlinear systems with time delay under asynchronous switching[J]. International Journal of Applied Mathematics and Computer Science, 2010, 20(3): 497-506. [本文引用:1]
[2]	Liu M, Shi P. Sensor fault estimation and tolerant control for It? stochastic systems with a descriptor sliding mode approach[J]. Automatica, 2013, 49(5): 1242-1250. [本文引用:1]
[3]	Liu Ming, Shi Peng, Zhang Li-xian, et al. Fault-tolerant control for nonlinear Markovian jump via proportional and derivative sliding mode observer technique[J]. IEEE Transactions on Circuits and Systems, 2011, 58(11): 2755-2764. [本文引用:1]
[4]	Ichalal D, Marx B, Ragot J, et al. New fault tolerant control strategies for nonlinear Takagi-Sugeno systems[J]. International Journal of Applied Mathematics and Computer Science, 2012, 20(3): 197-210. [本文引用:1]
[5]	肖冰, 胡庆雷, 马广富. 航天器执行机构部分失效故障的鲁棒容错控制[J]. 控制与决策, 2011, 26(6): 801-805. Xiao Bing, Hu Qing-lei, Ma Guang-fu. Robust fault tolerant attitude control for spacecraft under partial loss of actuator effectiveness[J]. Control and Decision, 2011, 26(6): 801-805. [本文引用:1]
[6]	Brambilla D, Capisani L M, Ferrara A, et al. Second order sliding mode observers for fault detection of robot manipulators[C]∥Proc 47th IEEE Conf Decision and Control, Cancun, Mexico, 2008: 2945-2954. [本文引用:1]
[7]	Henrik H. A model-based approach to fault-tolerant control[J]. International Journal of Applied Mathematics and Computer Science, 2012, 22(1): 67-86. [本文引用:1]
[8]	Jiang Jin, Zhang You-min. Accepting performance degradation in fault tolerant control system design[J]. IEEE Transaction on Control Systems Technology, 2006, 14(2): 284-292. [本文引用:1]
[9]	Sami M, Patton R J. Active fault tolerant control for nonlinear systems with simultaneous actuator and sensor faults[J]. International of Control, Automation and Systems, 2013, 11(6): 1149-1161. [本文引用:1]
[10]	陶洪峰, 胡寿松. 多故障并发不确定系统的鲁棒完整性容错控制[J]. 化工学报, 2010, 61(8): 2002-2007. Tao Hong-feng, Hu Shou-song. Robust tolerant control possessing integrity for uncertain systems with concurrent faults[J]. CIESC Journal, 2010, 61(8): 2002-2007. [本文引用:1]
[11]	赵博, 李成浩, 李元春. 基于故障在线估计的可重构机械臂分散容错控制[J]. 吉林大学学报: 工学版, 2014, 44(6): 1729-1735. Zhao Bo, Li Cheng-hao, Li Yuan-chun. Online fault estimation based decentralized fault-tolerant control for reconfigurable manipulators[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(6): 1729-1735. [本文引用:1]
[12]	赵博, 李元春. 考虑多传感器故障的可重构机械臂主动取代分散容错控制[J]. 控制与决策, 2014, 29(2): 226-230. Zhao Bo, Li Yuan-chun. Active substituting decentralized fault-tolerant control for reconfigurable manipulators with multi-sensor failures[J]. Control and Decision, 2014, 29(2): 226-230. [本文引用:1]
[13]	Zhao Bo, Li Yuan-chun. Local joint information based active fault tolerant control for reconfigurable manipulator[J]. Nonlinear Dynamics, 2014, 77(3): 859-876. [本文引用:1]
[14]	李元春, 陆鹏, 赵博. 可重构机械臂反演时延分散容错控制[J]. 控制与决策, 2012, 27(3): 446-450. Li Yuan-chun, Lu Peng, Zhao Bo. Backstepping time delay decentralized fault-tolerant control for reconfigurable manipulators[J]. Control and Decision, 2012, 27(3): 446-450. [本文引用:1]

2010

0.0

... 一些学者针对各类故障问题已经提出了相应的解决方法^[1,2,3,4] ...

2013

0.0

... 一些学者针对各类故障问题已经提出了相应的解决方法^[1,2,3,4] ...

2011

0.0

... 一些学者针对各类故障问题已经提出了相应的解决方法^[1,2,3,4] ...

2012

0.0

... 一些学者针对各类故障问题已经提出了相应的解决方法^[1,2,3,4] ...

2011

0.0

. 2011, 26(6):801-805 DOI:doi:10.1109/SYSTOL.2010.5676037

Robust fault tolerant attitude control for spacecraft under partial loss of actuator effectiveness

航天器执行机构部分失效故障的鲁棒容错控制

Xiao Bing , Hu Qing-lei , Ma Guang-fu.

肖冰, 胡庆雷, 马广富

A method of robust fault tolerant attitude control, based on adaptive sliding mode control is proposed for an on-orbiting spacecraft in the presence of partial loss of actuator effectiveness and external disturbance. In this approach, adaptive technique is employed to estimate the minimum value of actuator fault, and a sliding mode attitude controller is then designed to achieve fault tolerant control and external disturbance rejection. For the designers, the real minimum value of the fault is not required to be known in advance exactly, and the great robustness to fault is guaranteed. The simulation results of an application to spacecraft attitude adjustment maneuver show that great fault tolerant capability can be achieved even under partial loss of actuator effectiveness.

针对航天器在轨运行时受到外部干扰以及存在执行机构部分失效故障的问题, 提出一种基于自适应滑模控制的鲁棒容错控制方法. 该方法利用自适应算法估计执行机构故障的最小值, 并通过设计滑模变结构控制器来实现对故障的容错控制以及对干扰的抑制控制, 无需精确获得执行机构故障值, 从而使得设计的控制器对于故障具有一定的鲁棒性. 仿真结果表明了该方法对于姿态调节过程中执行机构部分失效故障具有较强的容错能力.

... 肖冰等^[5]通过滑模变结构控制器实现了故障容错和干扰抑制 ...

2008

0.0

... Brambilla等^[6]设计了次最优二阶滑模控制器并设计了观测器控制律 ...

2012

0.0

... Henrik等^[7]提出一种包含故障检测、隔离和重构的主动容错控制结构 ...

2006

0.0

... Jiang等^[8]针对线性系统可能存在的执行器、传感器及元部件故障,根据不同故障情况选择不同的控制器并修正系统控制命令 ...

2013

0.0

... Sami等^[9]结合T-S模糊模型,利用动态输出反馈控制实现对非线性系统执行器故障和传感器故障的容错 ...

2010

0.0

. 2010, 61(8):2002-2007

Robust tolerant control possessing integrity for uncertain systems with concurrent faults

多故障并发不确定系统的鲁棒完整性容错控制

Tao Hong-feng , Hu Shou-song.

陶洪峰, 胡寿松

摘　要：针对传统容错控制方法难以保证非线性系统在执行器和传感器多故障并发情形下的稳定性问题,研究了一类时滞不确定模糊系统的鲁棒完整性容错控制方法。建立了基于T-S模糊逻辑的不确定非线性模型,定义执行器和传感器故障阵的标准归一化形式,在利用Newton-Leibniz公式变换系统结构的基础上,根据线性矩阵不等式技术给出了鲁棒容错控制器存在的时滞相关性充分条件,以保证整个闭环系统在执行器和（或）传感器发生故障时的稳定性,同时满足给定的广义鲁棒性能约束,联合抑制扰动、初始状态和时滞状态对系统性能的影响。最后仿真结果验证了方法的必要性和可行性。

... 陶洪峰等^[10]利用鲁棒容错控制,保证了整个闭环系统在执行器和传感器多故障并发时的稳定性 ...

2014

0.0

. 2014, 44(6):1729-1735 DOI:doi:10.13229/j.cnki.jdxbgxb201406030

Online fault estimation based decentralized fault-tolerant control for reconfigurable manipulators

基于故障在线估计的可重构机械臂分散容错控制

Zhao Bo , Li Cheng-hao , Li Yuan-chun.

赵博, 李成浩, 李元春

To reduce the influence of module joint actuator and sensor failure on the controllability of the reconfigurable manipulator, an online fault estimation method based on the decentralized fault-tolerant control scheme was proposed. Based on the modularized property of the manipulator and Lyapunov stability theory, a decentralized adaptive sliding mode observer is constructed to estimate the actuator and sensor faults adaptively. Meanwhile, the nonlinear terms are approximated or compensated by neural networks. Then, the idea of non-singular fast terminal mode control was employed to achieve decentralized fault-tolerant control. Finally, numerical simulation was carried out for two 3-DOF reconfigurable manipulators with different configurations. The results demonstrate the effectiveness of the proposed fault-tolerant control scheme.

为了降低可重构机械臂模块关节执行器和传感器故障对其控制性能的影响,提出了一种基于故障在线估计的分散容错控制方法。基于可重构机械臂的模块化属性和Lyapunov稳定性理论,设计了分散自适应滑模观测器以实现执行器和传感器故障的在线自适应估计。同时采用神经网络对子系统非线性项进行逼近和补偿,并结合非奇异快速Terminal滑模思想实现了分散容错控制。最后,采用两种不同构形的三自由度可重构机械臂进行了仿真试验,结果表明,所设计的容错控制方法是有效的。

... 1 问题描述存在并发故障子系统i的动力学模型为^[11]: ...

2014

0.0

. 2014, 29(2):226-230 DOI:doi:10.13195/j.kzyjc.2012.1585

Active substituting decentralized fault-tolerant control for reconfigurable manipulators with multi-sensor failures

考虑多传感器故障的可重构机械臂主动取代分散容错控制

Zhao Bo , Li Yuan-chun.

赵博, 李元春

针对可重构机械臂系统位置传感器和速度传感器多故障,提出一种主动取代分散容错控制方法.基于可重构机械臂的模块化属性,设计正常工作模式下的分散神经网络控制器.利用微分同胚原理将子系统结构进行非线性变换,将传感器故障转化成伪执行器故障,设计分散滑模观测器以对多传感器故障进行实时检测,并利用其输出信号取代故障传感器信号,实现了多传感器故障情形下可重构机械臂的主动容错控制.仿真结果表明了所设计的容错控制方法的有效性.

... 引入一阶滤波器z_i将传感器故障转化为伪执行器故障^[12]: ...

2014

0.0

... 假设2 交联项h_iq,q·,q··有界且满足^[13]: ...

2012

0.0

. 2012, 27(3):446-450

Backstepping time delay decentralized fault-tolerant control for reconfigurable manipulators

可重构机械臂反演时延分散容错控制

Li Yuan-chun , Lu Peng , Zhao Bo.

李元春, 陆鹏, 赵博

For system actuator’s fault of reconfigurable manipulators with model parameters uncertainty, a fault-tolerant control algorithm based on backstepping design and time delay technology is proposed. This method uses the basic idea of the backstepping design, and compensates parameter uncertainty of the dynamic model and interconnection term by the neural networks. The proposed fault tolerant control does not need a fault diagnosis mechanism. Finally, simulation results show the effectiveness of the proposed algorithm.

针对存在模型参数不确定性的可重构机械臂系统执行器故障, 提出一种基于反演设计与时延技术相结合的容错控制方法. 该方法利用反演设计的基本思想, 通过神经网络补偿子系统动力学模型中的参数不确定项和关联项. 利用时延控制的逼近能力来补偿执行器的故障, 使得故障发生时能及时实现容错控制. 该方法具有不需要在线进行故障诊断的特点, 仿真结果表明了所提出控制方法的有效性.