考虑摩擦特性的机器人柔性关节鲁棒控制器设计

引用本文

陈健, 葛连正, 李瑞峰. 考虑摩擦特性的机器人柔性关节鲁棒控制器设计. 2015, 45(6): 1906-1912
CHEN Jian, GE Lian-zheng, LI Rui-feng. Design of robust controller for robot flexible joint with friction characteristic. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1906-1912 复制到剪切板

Permissions

考虑摩擦特性的机器人柔性关节鲁棒控制器设计

陈健, 葛连正, 李瑞峰

哈尔滨工业大学机器人技术与系统国家重点实验室,哈尔滨 150080

李瑞峰(1965-),男,教授,博士生导师.研究方向:工业机器人技术,智能服务机器人技术.E-mail:lrf100@hit.edu.cn

作者简介:陈健(1983-),男,博士.研究方向:工业机器人鲁棒控制.E-mail:phevanschen@gmail.com

基金:国家自然科学基金项目(61273339)

摘要

针对非线性摩擦特性对柔性关节机器人控制性能的影响,提出了采用 H_∞鲁棒原理设计控制器的方法。采用描述函数方法在频域分析非线性摩擦的描述函数,将非线性摩擦因素表达为相对于名义模型的逆加性不确定性。依据控制性能要求选取合理的控制量、噪声抑制和跟踪误差加权函数,将其转换为LMI最优问题进行求解。时域仿真结果表明:所设计控制器不仅具有鲁棒性能,并且具有快速、准确地跟踪轨迹指令的能力以及抑制干扰的作用。

关键词: 机械制造自动化; 柔性关节机器人; 非线性摩擦; 描述函数法; 鲁棒控制

中图分类号:TP241.2 文献标志码:A 文章编号:1671-5497(2015)06-1906-07

Design of robust controller for robot flexible joint with friction characteristic

CHEN Jian, GE Lian-zheng, LI Rui-feng

State Key Laboratory of Robotics and System, Harbin Institute of Technology, Harbin 150080, China

Abstract

A robust controller framework for flexible joint robot is presented, in which the effect of nonlinear friction on control performance is considered. The nonlinear friction is denoted as inverse additive output uncertainty relative to the nominal model. Based on this the describing function is analyzed in frequency domain, and the weighting function of nonlinear friction is further calculated. Combing the friction uncertainty, the Linear Matrix Inequality (LMI) optimization is proposed as the benchmark for controller design, which leads to good performance robustness. Simulation results show that the proposed controller can provide excellent command tracking and regulation performance.

Keyword: robot joint with flexibility; nonlinear friction; describing function method; robust control

Show Figures

0 引言

工业机器人系统大多采用谐波或RV(Rotate vector)减速器作为传动机构, 使得关节处不可避免地具有柔性。针对机器人关节柔性特性的控制器设计方法受到诸多学者的广泛关注及深入研究^{[1, 2, 3, 4, 5, 6]}。

柔性关节机器人的动力学方程可以被视为级联的两个子系统:连杆动力学和电机动力学。基于这种结构特点, Yim等^[7]提出一种鲁棒控制策略, 该方法包括计算力矩和鲁棒控制两部分, 采用非线性H_∞控制方法计算控制器增益, 获得了良好的轨迹跟踪性能。然而, 设计非线性H_∞控制器的过程非常复杂, 不利于实际应用。因此, 有必要考虑采用线性鲁棒控制原理设计柔性关节机器人控制器。Karlsson^[8]同时利用电机位置和末端加速度信息, 通过H_∞回路整形方法设计鲁棒控制器, 与仅考虑电机位置信息的H_∞回路整形方法相比, 提高了控制器的鲁棒性能。但是, 在线性H_∞优化方法控制器设计过程中, 首先要将非线性模型进行线性化处理^[9]。在系统中包含较强非线性因素的情况下, 基于特定操作点进行线性化方法所设计的控制器不能满足闭环系统在全部工作空间的跟踪误差、干扰抑制等性能要求。

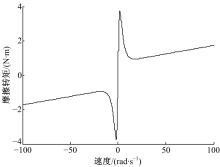
由于摩擦在低速时表现出强烈非线性, 使得机器人系统低速时的控制效果恶化。基于模型的摩擦补偿是一种有效提高系统性能的方法。经过长期研究, 人们提出了多种摩擦模型, 其中鬃毛模型、七参数模型、Lugre等摩擦模型具有较高的精度, 但是模型比较复杂, 参数辨识有一定难度^[10]。

现代工业机器人对控制器的要求不仅要具有良好的控制性能(例如:轨迹跟踪、干扰抑制等); 同时也需要对系统中存在的不确定因素具有鲁棒性能。但大多数针对柔性关节机器人设计的H_∞控制器, 忽略了传动环节存在的非线性动力学特性(例如:摩擦、迟滞等)。Moghaddam等^[11]在柔性关节机器人H_∞鲁棒控制器的设计过程中考虑了摩擦特性, 然而所采用的摩擦模型过度简化, 不能满足实际应用的要求, 并且非线性摩擦不确定性的计算过程复杂, 不便于实现。

本文针对柔性关节机器人传动中存在的非线性摩擦特性, 采用描述函数法构造非线性摩擦特性的不确定模型, 并将其转换为线性矩阵不等式(Linear matrix inequality, LMI)优化问题, 根据H_∞优化原理设计了柔性关节鲁棒控制器。

1 柔性关节机器人模型

1.1 柔性关节机器人模型

单关节柔性关节机器人模型可以看作是双惯量耦合系统, 电机通过具有弹性变形的旋转轴驱动刚性连杆, 根据牛顿第二定律可得柔性关节动力学方程为:

$\begin{matrix} \begin{matrix} J_{l} {\overset{\cdot \cdot}{θ}}_{l} + B_{l} {\overset{\cdot}{θ}}_{l} - K (θ_{m} - θ_{l}) = 0 (1) \\ J_{m} {\overset{\cdot \cdot}{θ}}_{m} + B_{m} {\overset{\cdot}{θ}}_{m} + τ_{f} + K (θ_{m} - θ_{l}) = τ_{m} (2) \end{matrix} \end{matrix}$

式中:θ _m、 $\begin{matrix} {\overset{\cdot}{θ}}_{m} \end{matrix}$ 、 $\begin{matrix} {\overset{\cdot \cdot}{θ}}_{m} \end{matrix}$ 和θ _l、 $\begin{matrix} {\overset{\cdot}{θ}}_{l} \end{matrix}$ 、 $\begin{matrix} {\overset{\cdot \cdot}{θ}}_{l} \end{matrix}$ 分别为电机和连杆的角位移、角速度、角加速度; J_m和J_l分别为电机和连杆的惯量; B_m和B_l分别为电机和连杆的阻尼系数; K表示柔性关节的扭转刚度系数; τ _m为电机输出转矩。

1.2 非线性摩擦力

经典的摩擦力模型包括粘滞和库伦摩擦, Feeny提出一种连续性光滑静态摩擦律^[12], 可用如下公式表述:

$\begin{matrix} τ_{f} = f_{v} v + (f_{c} + f_{cs} \sec h^{- 1} (βv)) \tanh (αv) (3) \end{matrix}$

式中:f_v为粘性摩擦因数; f_c为库伦摩擦因数; f_cs和α 构造Stribeck摩擦作用; β 保证方程在相对滑动速度为零时是连续的。

本文所采用参数的具体数值如表1所示^[13]。图1为摩擦模型特征曲线。

表1 柔性关节模型参数 Table 1 Flexible joint robot model parameters

	Figure Option View Download New Window
	图1 典型摩擦特征Fig.1 Typical friction characteristics

2 模型不确定性分析

2.1 非线性系统的描述函数

本文采用描述函数方法分析非线性摩擦不确定性, 并根据描述函数的频率响应幅值构造摩擦特性的线性时变动态模型。Schwartz^[14]提出一种通过Simulnk仿真获取描述函数的方法。将非线性系统分解为非线性部分和线性部分, 如图2所示。

	Figure Option View Download New Window
	图2 非线性系统Fig.2 Nonlinear system

考虑非线性部分输入的正弦信号为X_msinω t。F(x)为非线性函数, 输出信号y_N(t)是周期信号, 如果只考虑输出信号的基波分量, 对于正弦输入信号X_msinω t, 输出信号用傅里叶级数表达为:

$\begin{matrix} \begin{matrix} y_{N} (t) \approx Υ_{P 1} sinωt + Υ_{Q 1} cosωt (4) \\ y_{N} (t) \approx Im \{(Υ_{P 1} + j Υ_{Q 1}) e^{jωt}\} (5) \\ Υ_{P 1} = \frac{1}{π} \int_{0}^{2} F (X_{m} sinωt) sinωtd (ωt) (6) \\ Υ_{Q 1} = \frac{1}{π} \int_{0}^{2} F (X_{m} sinωt) cosωtd (ωt) (7) \end{matrix} \end{matrix}$

式中:Υ _P1、Υ _Q1为傅里叶系数。

非线性部分的描述函数定义为输出的基波和正弦输入的比值:

$\begin{matrix} G_{N} (X_{m}) = P (X_{m}) + jQ (X_{m}) = \frac{Υ_{P 1}}{X_{m}} + j \frac{Υ_{Q 1}}{X_{m}} (8) \end{matrix}$

式中:P $\begin{matrix} (X_{m}) \end{matrix}$ 和Q $\begin{matrix} (X_{m}) \end{matrix}$ 为线性谐波系数。

采用s-function实现式(3)的非线性摩擦特征, 在Simulink中构造结构框图, 如图3所示。通过仿真获得描述函数G_N $\begin{matrix} (X_{m}) \end{matrix}$ 增益如图4所示。结果表明描述函数增益对频率变化不敏感, 仅与幅值相关。

	Figure Option View Download New Window
	图3 描述函数的SIMULINK框图Fig.3 SIMULINK block diagram of describing function

	Figure Option View Download New Window
	图4 非线性摩擦描述函数增益Fig.4 Describing function gain of nonlinear friction

2.2 非线性摩擦的不确定性分析

通过等效的描述函数代替非线性摩擦特征, 将电机侧非线性摩擦表达为逆加性输出不确定性。包含不确定性的开环系统如图5所示。

电动机的名义模型和扰动模型分别为:

$\begin{matrix} \begin{matrix} G_{motor} (s) & = \frac{1}{J_{m} s + B_{m}} \\ {\tilde{G}}_{motor} (s) & = \frac{1}{J_{m} s + B_{m} + G_{N} (X_{m})} \end{matrix} 。 \end{matrix}$

式中:G_N $\begin{matrix} (X_{m}) \end{matrix}$ 为摩擦特性的描述函数。

	Figure Option View Download New Window
	图5 包含不确定性的开环系统Fig.5 Open-loop system including with uncertainty

名义和扰动模型之间的相对变化误差为:

$\begin{matrix} {({\tilde{G}}_{motor} (s))}^{- 1} = {(G_{motor} (s))}^{- 1} + W_{m} (s) Δ (s) (9) \end{matrix}$

式中:W_m $\begin{matrix} (s) \end{matrix}$ 为有界加权函数; Δ $\begin{matrix} (s) \end{matrix}$ 为范数有界不确定性传递函数, 且‖ Δ ‖ _∞≤ 1。

式(9)两端取H_∞范数可得:

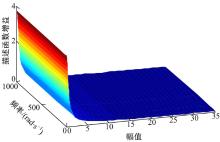
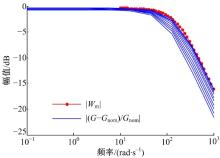
$\begin{matrix} \begin{matrix} {||\frac{{\tilde{G}}_{motor}}{G_{motor}} - 1||}_{\infty} \leq ‖ W_{m} ‖_{\infty} (10) \\ 即 : \\ |\frac{- N (s)}{J_{m} (jω) + B_{m} + N (s)}| \leq |W_{m} (jω)|, \forall ω (11) \end{matrix} \end{matrix}$

图6为不同幅值输入信号作用下式(11)的幅频特性曲线。利用鲁棒工具箱ucover命令, 可以求得加权函数W_m $\begin{matrix} (s) \end{matrix}$ 。

	Figure Option View Download New Window
	图6 摩擦特性的加权函数Fig.6 Weighting function of friction characteristics

3 鲁棒控制器设计

3.1 H_∞混合灵敏度控制器设计

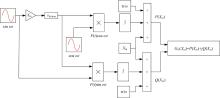
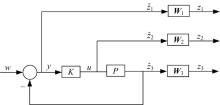
通过指定加权函数可以将控制性能要求转化为H_∞子最优控制问题。如图7所示, 加权函数W₁作用于信号跟踪误差y; 加权函数W₂作用于控制信号u; 加权函数W₃作用于对象输出 $\begin{matrix} {\hat{z}}_{3} \end{matrix}$ 。

	Figure Option View Download New Window
	图7 系统的加权H_∞混合灵敏度问题Fig.7 Weighted H_∞ mixed sensitivity problem of system

从w到z的闭环传递函数矩阵可表示为:

$\begin{matrix} T_{wz} = {[\begin{matrix} W_{1} S & W_{2} R & W_{3} T \end{matrix}]}^{T} (12) \end{matrix}$

T_wz同时包括灵敏度函数S(s)=(I+L(s))^-¹和补灵敏度函数T(s)=L(s)(I+L(s))^-¹; R表示对控制器输出的限制, 其中L(s)=P(s)K(s), 因此称为混合灵敏度问题。假设控制对象及加权函数具有如下状态空间表达形式:

P= $\begin{matrix} [A_{P}, B_{P}, C_{P}, D_{P}] \end{matrix}$ 关于状态x_p

W₁= $\begin{matrix} [A_{1}, B_{1}, C_{1}, D_{1}] \end{matrix}$ 关于状态x₁

W₂= $\begin{matrix} [A_{2}, B_{2}, C_{2}, D_{2}] \end{matrix}$ 关于状态x₂

W₃= $\begin{matrix} [A_{3}, B_{3}, C_{3}, D_{3}] \end{matrix}$ 关于状态x₃

则包括加权函数的扩展系统状态方程为:

$\begin{matrix} \begin{matrix} [\begin{matrix} {\overset{\cdot}{x}}_{1} \\ {\overset{\cdot}{x}}_{2} \\ {\overset{\cdot}{x}}_{3} \\ {\overset{\cdot}{x}}_{p} \\ z_{1} \\ z_{2} \\ z_{3} \\ y \end{matrix}] = [\begin{matrix} A_{1} & - B_{1} C_{p} & - B_{1} D_{p} \\ A_{2} & B_{2} \\ A_{3} & B_{3} C_{p} & B_{3} D_{p} \\ A_{p} & B_{p} \\ C_{1} & - D_{1} C_{p} & D_{1} & - D_{1} D_{p} \\ C_{2} & D_{2} \\ C_{3} & D_{3} C_{p} & D_{3} D_{p} \\ - C_{p} & I & - D_{p} \end{matrix}] [\begin{matrix} x_{1} \\ x_{2} \\ x_{3} \\ x_{p} \\ w \\ u \end{matrix}] (13) \\ 即 : \{\begin{matrix} \overset{\cdot}{x} = Ax + B_{w} w + B_{u} u, \\ z = C_{z} x + D_{zw} w + D_{zu} u, \\ y = C_{y} x + D_{yw} w, \end{matrix} (14) \end{matrix} \end{matrix}$

对系统(14)设计反馈控制律K的状态空间表达式为:

$\begin{matrix} \{\begin{matrix} {\overset{\cdot}{x}}_{K} = A_{K} x_{K} + B_{K} y \\ u = C_{K} x_{K} + D_{K} y \end{matrix} (15) \end{matrix}$

通过LFT变换, 得到从w到z的闭环系统函数矩阵为:

$\begin{matrix} T_{wz} = (\begin{matrix} \begin{matrix} A + B_{u} D_{K} C_{y} & B_{u} C_{K} \\ B_{K} C_{y} & A_{K} \end{matrix} & \begin{matrix} B_{w} + B_{u} D_{K} D_{yw} \\ B_{K} D_{yw} \end{matrix} \\ \begin{matrix} C_{z} + D_{zu} D_{K} C_{y} & D_{zu} C_{K} \end{matrix} & D_{zw} + D_{zu} D_{K} D_{yw} \end{matrix}) (16) \end{matrix}$

则加权H_∞最优混合灵敏度问题转化为找寻一个稳定控制器K, 使其满足:

$\begin{matrix} {||T_{wz} = (\begin{matrix} A_{CL} & B_{CL} \\ C_{CL} & D_{CL} \end{matrix})||}_{\infty} < 1 (17) \end{matrix}$

式(17)成立的条件是, 存在对称正定矩阵Q使得下面的不等式成立:

$\begin{matrix} (\begin{matrix} {A^{T}}_{CL} Q + Q A_{CL} & Q B_{CL} & {C^{T}}_{CL} \\ {B^{T}}_{CL} Q & - γI & {D^{T}}_{CL} \\ C_{CL} & D_{CL} & - γI \end{matrix}) < 0 (18) \end{matrix}$

综上, 控制器可以通过以下优化问题获得:

$\begin{matrix} \{\begin{matrix} \underset{A_{K}, B_{K}, C_{K}, D_{K}}{Minimise} γ & (a) \\ subjecttoQ > 0 & (b) \\ (\begin{matrix} {A^{T}}_{CL} Q + Q A_{CL} & Q B_{CL} & {C^{T}}_{CL} \\ {B^{T}}_{CL} Q & - γI & {D^{T}}_{CL} \\ C_{CL} & D_{CL} & - γI \end{matrix}) < 0 & (c) \end{matrix} (19) \end{matrix}$

不等式中包含Q和A_K、B_K、C_K、D_K的乘积项, 因此, 式(19c)是非线性的。通过换元法^[15]可以将式(19c)转换为线性不等式, 并采用LMI优化方法求解。

3.2 鲁棒稳定性分析

由控制器K和包含不确定性的开环系统组成的闭环系统如图8(a)所示, 图8(b)为用于鲁棒性分析的M-Δ 结构。

	Figure Option View Download New Window
	图8 包含不确定性的广义系统及用于鲁棒性分析的M-Δ 结构Fig.8 Augment system with uncertainty and M-Δ structure for robust stability analysis

通过LFT变换求得从输入[u_Δ w]^T到输出[z_Δ z]^T的闭环传递函数矩阵为:

$\begin{matrix} N = [\begin{matrix} N_{11} & N_{12} \\ N_{21} & N_{22} \end{matrix}] (20) \end{matrix}$

式中:N₁₁记为M。

定理1 非结构化摄动下的鲁棒稳定性^[13]。假设标称系统M(s)是稳定的, 并且摄动也是稳定的, 那么图8(b)中的M-Δ 系统对于所有满足‖ Δ ‖ _∞≤ 1的扰动Δ 都是稳定的(即具有鲁棒稳定性), 当且仅当:

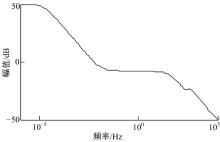
$\begin{matrix} \bar{σ} (M (jω)) < 1, \begin{matrix} \forall w \end{matrix} \Leftrightarrow ‖ M ‖_{\infty} < 1 。 \end{matrix}$

因此只要保证传递函数M的频率响应幅值小于0 dB, 即可确定控制器对扰动Δ 具有稳定鲁棒性。

4 控制器性能分析及非线性系统仿真

式(12)中的加权函数分别选取为:

W₁ $\begin{matrix} (s) \end{matrix}$ = $\begin{matrix} \frac{1}{100} \end{matrix} \begin{matrix} [\frac{s + 10000}{s + 0.0001}] \end{matrix}$ ;

W₂ $\begin{matrix} (s) \end{matrix}$ =10; W₃ $\begin{matrix} (s) \end{matrix}$ = $\begin{matrix} \frac{s + 10}{100} \end{matrix}$

通过LMI求解最优问题(式(19))得到6阶控制器K如下:

$\begin{matrix} \begin{matrix} C_{K} = [0 0.010 89 - 0.06235 3.731 \\ 1.609 - 1674]; \\ D_{K} = [\begin{matrix} 0 \end{matrix}]; \end{matrix} \end{matrix}$

$\begin{matrix} \begin{matrix} A_{K} = [\begin{matrix} - 1 & 0.00034 & - 0.00975 & 0.00063 & 0 & - 0.08792 \\ 0.005574 & - 519.6 & 2318 & - 149.1 & 0.992 & 14400 \\ 0.00221 & - 974.2 & - 833.8 & 58.85 & - 1.69 & - 22330 \\ 0 & - 0.335 & 2.859 & - 7.615 & - 220.9 & 3290 \\ 0 & 27.84 & 90.24 & - 43.45 & - 11110 & - 96.73 \\ 0 & - 11.5 & 17.95 & 61.85 & - 96.38 & - 28020 \end{matrix}]; \\ B_{K} = {[\begin{matrix} 0 & 0.00088 & 0.00026 & - 0.3929 & 0.1177 & - 105.7 \end{matrix}]}^{T} 。 \end{matrix} \end{matrix}$

最小γ 值为0.863, 因此闭环系统的H_∞范数小于1, 满足式(17)的名义性能条件。控制器 $\begin{matrix} |K| \end{matrix}$ 增益如图9所示。

	Figure Option View Download New Window
	图9 控制器 $\begin{matrix} \|K\| \end{matrix}$ 的增益Fig.9 Controller gain of $\begin{matrix} \|K\| \end{matrix}$

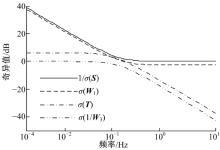
式(12)中的性能W₁和鲁棒性 $\begin{matrix} {W_{3}}^{- 1} \end{matrix}$ 的边界以及闭环传递函数S和T的奇异值如图10所示。其中, S^-¹的最小奇异值在W₁的幅值响应以上, T的最大奇异值在 $\begin{matrix} {W_{3}}^{- 1} \end{matrix}$ 幅值响应以下, 这表明期望选取的加权函数能够满足性能和鲁棒性要求。图11表明式(20)中传递函数M的幅值小于1(0 dB), 满足定理1的条件, 即闭环系统对扰动Δ 具有鲁棒稳定性。

	Figure Option View Download New Window
	图10 性能指标和鲁棒指标的奇异值Fig.10 Singular values of the performance and robustness

	Figure Option View Download New Window
	图11 传递函数M的幅值Fig.11 Magnitude of transfer function M

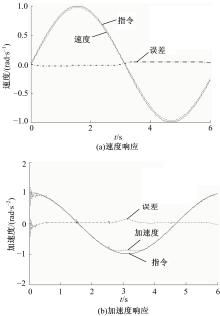
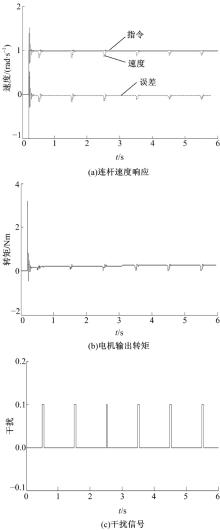
最后, 在Simulink中建立柔性关节动力学模型。通过时域仿真进一步说明所设计的鲁棒控制器的指令跟踪性能及扰动抑制性能是满足要求的。图12为闭环系统在正弦输入下的连杆速度和加速度响应曲线。从图12(a)可以看出, 速度信号可以快速跟踪指令信号并保持较小的误差(最大误差为0.083 rad/s)。图13为闭环系统在阶跃输入并且在连杆处施加扰动的响应曲线。从图13(a)可以看出, 对于阶跃输入, 速度信号具有较好的瞬态响应特性, 而且对干扰输入具有抑制作用。实际中工业机器人只能采集电机的输出信号, 因此在仿真过程中将电机侧输出作为反馈信号。这也是图13(a)中产生静态误差的原因之一。

	Figure Option View Download New Window
	图12 正弦输入信号的闭环系统响应Fig.12 Closed-loop system response of sinusoidal input signal

	Figure Option View Download New Window
	图13 阶跃输入和干扰信号的闭环系统响应Fig.13 Closed-loop system response of step input signal with disturbance

5 结束语

针对非线性摩擦对柔性关节机器人控制性能造成的影响, 提出了一种设计线性H_∞鲁棒控制器的方法。采用描述函数方法获取摩擦特性的加权函数, 并通过逆加性不确定性建立包含非线性摩擦的扩展系统。根据H_∞混合灵敏度方法设计鲁棒控制器, 并将其转换为LMI最优问题, 所设计控制器不仅具有鲁棒稳定性, 而且能够满足系统轨迹跟踪、干扰抑制等性能要求。通过非线性模型的闭环系统时域仿真表明了所设计控制器具有较好的指令跟踪性能、扰动抑制能力和鲁棒稳定性。本文所提出的控制器设计方法具有一定通用性, 同样适用于传动环节具有迟滞、间隙等其他非线性特征的情况。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Moberg S, Hanssen S. On feedback linearization for robust tracking control of flexible joint robots[J]. World Congress, 2008, 17(1): 12218-12223. [本文引用:1]
[2]	Yeon J S, Park J H. Practical robust control for flexible joint robot manipulators[C]∥IEEE International Conference on Robotics and Automation, California, USA, 2008: 3377-3382. [本文引用:1]
[3]	Akbari M E, Alizadeh G, Khanmohammadi S, et al. Nonlinear H_∞ controller for flexible joint robots with using feedback linearization[J]. International Journal on Computer Science & Engineering, 2011, 3(2): 451-466. [本文引用:1]
[4]	Elmaraghy H A, Lahdhiri T. Robust linear control of flexible joint robot systems[J]. Journal of Intelligent and Robotic Systems, 2002, 34(4): 335-356. [本文引用:1]
[5]	Patel A, Neelgund R, Wathore A, et al. Robust control of flexible joint robot manipulator[C]∥Industrial Technology, Mumbai, 2006: 649-653. [本文引用:1]
[6]	Akbari M, Alizadeh G, Khanmohammadi S, et al. Nonlinear H_∞ controller for flexible joint robots with using feedback linearization[J]. International Journal of Engineering Science, 2011, 3(4): 451-466. [本文引用:1]
[7]	Yim J G, Yeon J S, Park J H, et al. Robust control using recursive design method for flexible joint robot manipulator[C]∥IEEE International Conference on Robotics and Automation, Roma, Italy, 2007: 3805-3810. [本文引用:1]
[8]	Karlsson A P. Tool position estimation of a flexible industrial robot using recursive bayesian methods[J]. Proceedings IEEE International Conference on Robotics & Automation, 2012, 20(10): 5234-5239. [本文引用:1]
[9]	Nassirharand A, Firdeh S R M. Computer-aided design of nonlinear H_∞ controllers using describing functions[C]∥Computer Aided Control System Design, 2006 IEEE International Conference on Control Applications, Munich, Germany, 2006: 1952-1957. [本文引用:1]
[10]	刘国平. 机械系统中的摩擦模型及仿真[D]. 西安: 西安理工大学机械与精密仪器工程学院, 2007: 35-37. Liu Guo-ping. Mechanical friction system model and simulation[D]. Xi'an: Mechanical and Precision Instrument Engineering, Xi'an University of Technology, 2007: 35-37. [本文引用:1]
[11]	Moghaddam M, Andrew A. On robust control of flexible joint robots using describing function and sector bounded nonlinearity descriptions[J]. Journal of Intelligent and Robotic Systems, 1997, 20(2): 333-348. [本文引用:1]
[12]	Feeny B, Moon F C. Chaos in a forced dry-friction oscillator: experiments and numerical modelling[J]. Journal of Sound & Vibration, 1994, 170(3): 303-323. [本文引用:1]
[13]	Wernholt E, Gunnarsson S. Nonlinear identification of a physically parameterized robot model[J]. Control Engineering, 2006, 14(1): 143-148. [本文引用:2]
[14]	Schwartz C, Gran R. Describing function analysis using Matlab and simulink[J]. Control Systems, 2001, 21(4): 19-26. [本文引用:1]
[15]	Scherer C, Gahinet P, Chilali M. Multiobjective output-feedback control via LMI optimization[J]. IEEE Transactions on Automatic Control, 1997, 42(7): 896-911. [本文引用:1]

2008

0.0