基于向量的鲁棒分数阶比例微分控制器参数求解算法

引用本文

王春阳, 蔡年春, 李明秋, 刘雪莲. 基于向量的鲁棒分数阶比例微分控制器参数求解算法. 2015, 45(6): 1933-1940
WANG Chun-yang, CAI Nian-chun, LI Ming-qiu, LIU Xue-lian. Robust fractional order proportional differential controller parameters algorithm based on phasor. Journal of Jilin University Engineering and Technology Edition, 2015, 45(6): 1933-1940 复制到剪切板

Permissions

基于向量的鲁棒分数阶比例微分控制器参数求解算法

王春阳, 蔡年春, 李明秋, 刘雪莲

长春理工大学电子信息工程学院,长春 130022

作者简介:王春阳(1964-),女,教授,博士生导师.研究方向:鲁棒分数阶控制器.E-mail:wangchunyang19@cust.edu.cn

基金:吉林省科技发展计划项目(20130102025JC)

摘要

以分数阶比例微分(FOPD)控制器为例,详细地论述了基于向量的鲁棒FOPD控制器参数求解过程,证明了该方法求解的控制器参数具有唯一性,并编写了基于MATLAB环境下FOPD控制器参数求解算法程序,实现了面向不同相位裕度、不同穿越频率以及不同被控对象的鲁棒FOPD控制器系统校正。结果表明,本文算法不仅简化了控制器参数求解过程,减少了计算量,而且求得的控制器参数唯一且有效。

关键词: 人工智能; 控制理论; 鲁棒分数阶控制器; 分数阶比例微分; 参数求解

中图分类号:TP13 文献标志码:A 文章编号:1671-5497(2015)06-1933-08

Robust fractional order proportional differential controller parameters algorithm based on phasor

WANG Chun-yang, CAI Nian-chun, LI Ming-qiu, LIU Xue-lian

School of Electronic and Information Engineering, Changchun University of Science and Technology, Changchun 130022, China

Abstract

Using an example of Fractional Order Proportional Differential (FOPD) controller, the parameter calculation procedure of the robust FOPD controller based on phasor method is discussed in detail. It is proved that the calculated controller parameters based on phasor method are unique. Besides, the proposed algorithm is programmed in Matlab. According to Matlab programs, the FOPD controller parameters solution algorithm and the FOPD controller are respectively designed for the systems compensation following the different given phase margin, different given gain crossover frequency and different given controlled objects. This study results show that not only the parameter calculation procedure of fractional order controllers is simplified and the amount of calculation is reduced, but also the calculated controller parameters are unique and valid.

Keyword: artificial intelligence; control theory; robust fractional order controller; fractional order proportional derivative(FOPD); parameter calculation

Show Figures

在电机控制系统中常存在有效负荷的惯性参数不稳定或者其在某一个小的范围内变动, 导致系统开环增益变化的问题^[1]。陈阳泉等^[2]在稳定性裕度基础上增加增益鲁棒性条件, 提出了鲁棒分数阶控制器设计方法, 即要求系统开环增益变化时, 系统阶跃响应超调量几乎不变, 其频域特性要求伯德图相位在截止频率ω _c周围是平坦的。在文献[1-11]中陈阳泉教授等证实了增益鲁棒性分数阶控制器既能满足系统稳定, 又能满足系统开环增益鲁棒性。然而, 文献[8-11]中增益鲁棒性分数阶控制器参数求解过程非常复杂、计算量大。对于不同的被控对象, 增益鲁棒性分数阶控制器参数求解方程是不同的, 难以程序化求解增益鲁棒性分数阶控制器参数。

本文提出了一种基于向量的增益鲁棒性分数阶控制器参数求解简化算法, 该方法根据映射原理预先在复平面内建立控制器向量模型, 进而利用复平面内几何关系建立方程求解控制器参数。

1 控制器向量模型

利用映射方法将控制器映射到复平面, 建立控制器的向量模型。

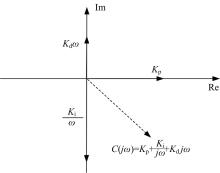
(1)整数阶控制器向量模型(见图1)为:

$\begin{matrix} \begin{matrix} C (s) = K_{p} + K_{i} / s + K_{d} s (1) \\ C (jω) = K_{p} + \frac{K_{i}}{jω} + K_{d} jω (2) \end{matrix} \end{matrix}$

	Figure Option View Download New Window
	图1 整数阶向量模型Fig.1 IOPID controller vector model

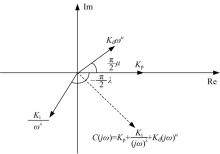
(2)分数阶控制器向量模型(见图2)为:

$\begin{matrix} \begin{matrix} C (s) = K_{p} + \frac{K_{i}}{s^{λ}} + K_{d} s^{u}, 0 < λ, u < 2 (3) \\ C (jω) = K_{p} + \frac{K_{i}}{{(jω)}^{λ}} + K_{d} {(jω)}^{u}, 0 < λ, u < 2 (4) \end{matrix} \end{matrix}$

	Figure Option View Download New Window
	图2 分数阶向量模型Fig.2 FOPID controller vector model

从图1中可以看出, 复平面内整数阶控制器向量是通过K_p、K_i、K_d调节正实轴、负虚轴和正虚轴上的向量(即比例向量、积分向量和微分向量)长度, 从而调整控制器向量的变化。整数阶控制器的比例向量、积分向量和微分向量是固定在实轴和虚轴上的, 只能构成在复平面右半平面的任一向量。整数阶控制器通过K_p、K_i、K_d分别调节比例作用、积分作用和微分作用。

从图2可以看出, 复平面内分数阶控制器向量是通过K_p、K_i、K_d分别调节比例向量、积分向量和微分向量的长度; λ 和μ 分别调整积分向量和微分向量的角度。分数阶控制器的积分向量和微分向量可以在复平面内旋转, 和比例向量一起构成的分数阶控制器向量可以构成复平面内的任一向量。

2 基于向量的控制器参数求解

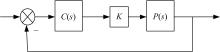
增益鲁棒性控制器参数求解是根据在复平面性能指标向量G, 求得一个校正向量L, 使其校正被控对象向量P达到要求的性能指标向量G, 即L· P=G。然后用控制器向量C去逼近校正向量L, 就可以得到控制器参数方程。基于向量的控制器参数求解步骤如下:

(1)写出被控对象的向量形式及角速度。

被控对象为P(s)写成向量形式为:

$\begin{matrix} P (jω) = |P (jω)| ∠P (jω) (5) \end{matrix}$

被控对象的角速度:

$\begin{matrix} {(\frac{d (Arg [P (jω)])}{dω})}_{ω = ω_{c}} = φ_{P} (6) \end{matrix}$

(2)根据系统要求, 写出性能指标向量G $\begin{matrix} (jω) \end{matrix}$ 。

稳定性性能指标:根据开环系统在ω _c处的相位裕度φ _m可以得到稳定性性能指标向量为:

$\begin{matrix} G (j ω_{c}) = 1 ∠ (φ_{m} - 180 °) (7) \end{matrix}$

鲁棒性性能指标:为保证系统对增益变化的鲁棒性, 增加增益变化的鲁棒性条件, 即要求系统开环传递函数的相位在穿越频率ω _c附近是平坦的^{[1, 2, 8, 9, 10, 11, 12, 13]}。

$\begin{matrix} {(\frac{d (Arg [G (jω)])}{dω})}_{ω = ω_{c}} = 0 (8) \end{matrix}$

即要求性能指标向量在穿越频率ω _c处的角速度为0。

(3)根据L· P=G, 求得校正向量L。

根据稳定性性能指标向量(式(7))和被控对象向量(式(5)), 由L· P=G可求得校正向量:

$\begin{matrix} L (j ω_{c}) = \frac{1}{|P (j ω_{c})|} ∠ (φ_{m} - ∠P (j ω_{c}) - 180 °) (9) \end{matrix}$

又根据鲁棒性性能指标(式(8)), 由L· P=G可知在频率ω _c处校正向量角速度φ _L和被控对象角速度φ _P之和等于0, 则校正向量的角速度为:

$\begin{matrix} φ_{L} = - φ_{P} (10) \end{matrix}$

(4)用控制器向量去逼近校正向量, 也就是说控制器向量与校正向量具有相同的模值、相角以及角速度。从而得到控制器参数求解的方程。

3 FOPD控制器参数求解

分数阶比例微分(FOPD)控制器传递函数为:

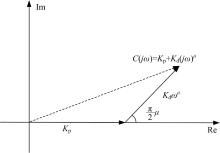
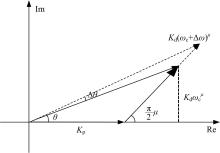
$\begin{matrix} C (s) = K_{p} + K_{d} s^{μ} (11) \end{matrix}$

FOPD控制器向量(见图3)表示为:

$\begin{matrix} C (jω) = K_{p} + K_{d} {(jω)}^{μ} (12) \end{matrix}$

	Figure Option View Download New Window
	图3 FOPD控制器向量Fig.3 FOPD controller vector model

令θ =φ _m-Arg $\begin{matrix} [P (j ω_{c})] \end{matrix}$ -180° 和A= $\begin{matrix} \frac{1}{|P (j ω_{c})|} \end{matrix}$ , 即L $\begin{matrix} (j ω_{c}) \end{matrix}$ =A∠θ 。其中, A为校正向量模值; θ 为校正向量相角。

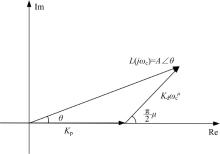
由控制参数求解步骤(4), 用FOPD控制器向量去逼近校正向量, 控制器向量与校正向量模值和相角相等, 即满足稳定性性能指标。由图4和三角形余弦定理可以得到:

$\begin{matrix} \begin{matrix} K_{d} ω_{c}^{μ} = \sqrt{K_{p}^{2} + A^{2} - 2 K_{p} Acosθ} = B (13) \\ \cos (π - \frac{π}{2} μ) = \frac{K_{p}^{2} + B^{2} - A^{2}}{2 B K_{p}} = \frac{K_{p} - Acosθ}{B} (14) \end{matrix} \end{matrix}$

	Figure Option View Download New Window
	图4 FOPD控制器向量和校正向量Fig.4 FOPD controller vector and the calibration vector

如图5所示, 当ω _c变为ω _c+Δ ω , Δ ω → 0时, 控制向量的角度变化量为Δ θ :

$\begin{matrix} \begin{matrix} Δθ = C (j (ω_{c} + Δω)) - C (j ω_{c}) = \\ \arctan \frac{K_{d} {(ω_{c} + Δω)}^{μ} \sin (\frac{π}{2} μ)}{K_{p} + K_{d} {(ω_{c} + Δω)}^{μ} \cos (\frac{π}{2} μ)} - \\ \arctan \frac{K_{d} ω_{c}^{μ} \sin (\frac{π}{2} μ)}{K_{p} + K_{d} ω_{c}^{μ} \cos (\frac{π}{2} μ)} (15) \end{matrix} \end{matrix}$

	Figure Option View Download New Window
	图5 控制器向量角度变化量Δ θ Fig.5 Angle change of the controller vector Δ θ

由第2节步骤(4), 用FOPD控制器向量去逼近校正向量, 控制器向量角速度与校正向量角速度相等, 即满足增益鲁棒性性能指标:

$\begin{matrix} \begin{matrix} \lim_{Δω \to 0} (\frac{∠C (j (ω_{c} + Δω)) - ∠C (j ω_{c})}{Δω}) = \\ \lim_{Δω \to 0} (\frac{∠L (j (ω_{c} + Δω)) - ∠L (j ω_{c})}{Δω}) (16) \end{matrix} \end{matrix}$

可以得到：

$\frac{μ K_{p} K_{d} ω_{c}^{μ - 1} \sin (\frac{π}{2} μ)}{{[K_{p} + K_{d} ω_{c}^{μ} \cos (\frac{π}{2} μ)]}^{2} + {[K_{d} ω_{c}^{μ} \sin (\frac{π}{2} μ)]}^{2}} = φ_{L} (17)$

图5中有几何关系:K_d $\begin{matrix} ω_{c}^{μ} \end{matrix}$ sin $\begin{matrix} (\frac{μπ}{2}) \end{matrix}$ =Asinθ 和 $\begin{matrix} {[K_{p} + K_{d} ω_{c}^{μ} \cos (\frac{μπ}{2})]}^{2} \end{matrix}$ + $\begin{matrix} {[K_{d} ω_{c}^{μ} \sin (\frac{μπ}{2})]}^{2} \end{matrix}$ =A², 所以得到:

$\begin{matrix} \frac{μ K_{p} sinθ}{A ω_{c}} = φ_{L} (18) \end{matrix}$

联立式(13)(14)(18)可以求得K_p、K_d和μ 。

4 FOPD控制器参数的唯一性

由第3节可知A, θ 和φ _L分别是校正向量的模值、相角和角速度, ω _c为穿越频率, 且A, θ , φ _L和ω _c均与K_p和μ 无关。其中A, ω _c> 0, K_p∈ (0, +¥ )。下面讨论方程(13)(14)和(18)求解的参数唯一性。

(1)由方程(18)可求得μ 关于K_p的函数g₁ $\begin{matrix} (K_{p}) \end{matrix}$ :

$\begin{matrix} μ = g_{1} (K_{p}) = \frac{A φ_{L} ω_{c}}{K_{p} sinθ} (19) \end{matrix}$

由0< μ < 2和式(19)可知, $\begin{matrix} \frac{A φ_{L} ω_{c}}{sinθ} \end{matrix}$ > 0。所以g₁ $\begin{matrix} (K_{p}) \end{matrix}$ 的导数g'₁ $\begin{matrix} (K_{p}) \end{matrix}$ =- $\begin{matrix} \frac{A φ_{L} ω_{c}}{K_{p}^{2} sinθ} \end{matrix}$ < 0。

(2)由方程(14)可得:

$\begin{matrix} \cos (\frac{π}{2} μ) = \frac{Acosθ - K_{p}}{\sqrt{{(K_{p} - Acosθ)}^{2} + A^{2} si n^{2} θ}} (20) \end{matrix}$

由式(20)可知, μ 关于K_p的连续函数。

当0< K_p< Acosθ 时, 由式(18)可得:

$\begin{matrix} \cos (\frac{π}{2} μ) = \frac{1}{\sqrt{1 + \frac{A^{2} si n^{2} θ}{{(Acosθ - K_{p})}^{2}}}} (21) \end{matrix}$

等式(21)左边在0< μ < 2时是关于μ 单调递减函数, 等式(19)右边在0< K_p< Acosθ 时是关于K_p单调递减函数。所以μ 在0< K_p< Acosθ 是关于K_p的单调递增函数。

当Acosθ < K_p时, 由式(20)可得:

$\begin{matrix} \cos (\frac{π}{2} μ) = - \frac{1}{\sqrt{1 + \frac{A^{2} si n^{2} θ}{{(K_{p} - Acosθ)}^{2}}}} (22) \end{matrix}$

等式(22)右边在Acosθ < K_p时依然是关于K_p的单调递减函数。所以μ 在Acosθ < K_p时是关于K_p的单调递增函数。

由式(14)所得μ 关于K_p的函数g₂(K_p)为:

$\begin{matrix} μ = g_{2} (K_{p}) = \frac{2}{π} \arccos \frac{Acosθ - K_{p}}{\sqrt{K_{p}^{2} + A^{2} - 2 K_{p} Acosθ}} (23) \end{matrix}$

g₂ $\begin{matrix} (K_{p}) \end{matrix}$ 是关于K_p(K_p∈ $\begin{matrix} (0, Acosθ) \end{matrix}$ ∪ $\begin{matrix} (Acosθ, \infty) \end{matrix}$ )的单调递增函数, 即g'₂ $\begin{matrix} (K_{p}) \end{matrix}$ > 0。

联立方程(14)和(18)得到关于K_p的函数:

$\begin{matrix} \begin{matrix} h (K_{p}) = g_{2} (K_{p}) - g_{1} (K_{p}) = \\ \frac{2}{π} \arccos \frac{Acosθ - K_{p}}{\sqrt{K_{p}^{2} + A^{2} - 2 K_{p} Acosθ}} - \frac{A φ_{L} ω_{c}}{K_{p} sinθ} (24) \end{matrix} \end{matrix}$

函数h $\begin{matrix} (K_{p}) \end{matrix}$ 的导函数h' $\begin{matrix} (K_{p}) \end{matrix}$ 为:

$\begin{matrix} h' (K_{p}) = g'_{2} (K_{p}) - g'_{1} (K_{p}) (25) \end{matrix}$

综上可知函数h(K_p)的导函数h'(K_p)在K_p∈ (0, Acosθ )∪ (Acosθ , ¥ )是恒大于0, h(K_p)为单调增函数。所以方程(14)和(18)在K_p∈ (0, Acosθ )∪ (Acosθ , ¥ )的解具有唯一性。

当K_p=Acosθ 时, 由式(20)得μ =1, 代入方程(11)得到K_d=Asinθ /ω _c。三个参数均唯一。

综上所述, 由方程(14)(18)求得的K_p∈ (0, ¥ )是唯一解, 代入参数方程(18)和(13)求得的μ 、K_d均为唯一解。所以基于向量求解的FOPD控制器参数是唯一的。

5 FOPD控制器参数求解

基于向量的增益鲁棒性FOPD控制器参数求解的总体思路为:先根据L· P=G得到校正向量, 然后利用控制器向量逼近校正向量得到控制器参数方程。

由于控制器参数方程(13)(14)和(18)只与校正向量模值、相角和角速度有关系, 所以可以将控制器参数方程进行Matlab程序化。其中, 校正向量的模值、相角和角速度可以根据被控对象的模值、相角和角速度由L· P=G求得。

Matlab程序编写如下:

syms y m n k f A B

ω =ω _c;

k=φ _m;

m=M_p;

n=F_p;

f=R_p;

A=10^∧(-m/20);

θ =(k-180-n)* pi/180;

F=-f;

y=f(x);

ezplot(y)

hold on;

y=g(x);

ezplot(y)

其中, M_p为被控对象向量模值; F_p为被控对象向量相角; R_p为被控对象向量角速度; F为校正向量角速度; f(x)和g(x)分别代表方程(14)和(18)。只需要输入被控对象向量模值、相角和角速度就可以求得K_p和μ , 然后代入方程(13)求得K_d。

6 仿真实例验证

利用第5节FOPD控制器参数求解Matlab程序, 求解不同相位裕度(例1和例2)、不同穿越频率(例1和例3)以及不同被控对象(例1和例4)条件下的增益鲁棒性FOPD控制器参数。并给出了系统开环伯德图和系统开环增益K(见图6)分别取0.9、1和1.1(开环增益变化± 10%)的阶跃响应图。

	Figure Option View Download New Window
	图6 FOPD控制系统结构框图Fig.6 Structure diagram of FOPD control system

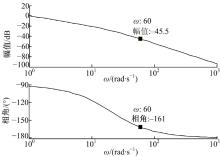
例1 被控对象P(s)= $\begin{matrix} \frac{1}{s (Ts + 1)} \end{matrix}$ , 其中T=0.05 s, 穿越频率ω _c=60 rad/s, 相位裕度φ _m=70° 。

根据被控对象P(s)的伯德图(见图7), 可以得到被控对象P在ω =60 rad/s处的模值为-45.5 dB, 相角为-161° 。

	Figure Option View Download New Window
	图7 被控对象P(s)在60 rad/s的模值和相角Fig.7 Plant’ s amplitude and phase in the 60 rad/s

由式(6)可得到被控对象P(s)的角速度 $\begin{matrix} {φ_{p}|}_{ω = 60} \end{matrix}$ =-0.005。根据第5节FOPD控制器参数求解Matlab程序, 输入ω =60; k=70; m=-45.5; n=-161; f=-0.005, 得到FOPD控制器参数K_p和μ , 如图8所示。从而求得K_p=84.92, μ =0.8563并代入方程(13)可以求得K_d=4.5085, 得控制器传递函数为:

$\begin{matrix} C_{1} (s) = 84.92 + 4.5085 s^{0.8563} (26) \end{matrix}$

	Figure Option View Download New Window
	图8 例1所求FOPD控制器参数K_p和μ Fig.8 K_pversus μ with FOPD controller in case 1

可以得到系统开环传递函数伯德图以及系统开环增益变化10%的系统阶跃响应图(见图9)。

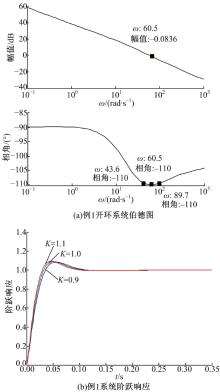	Figure Option View Download New Window
	图9 例1所求系统开环传递函数伯德图和阶跃响应Fig.9 Bode plot and unit step responses with designed FOPD controller in case 1

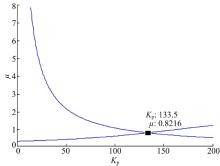
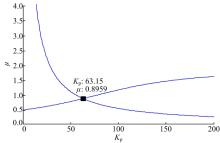
例2 被控对象P(s)= $\begin{matrix} \frac{1}{s (Ts + 1)} \end{matrix}$ , 其中T=0.05 s, 穿越频率ω _c=60 rad/s, 相位裕度φ _m=50° 。

根据Matlab求解程序, 可得FOPD控制器参数K_p=133.5, μ =0.8216(见图10), K_d=3.4157, 进而得出控制器传递函数为:

$\begin{matrix} C_{2} (s) = 133.5 + 3.4157 s^{0.8216} (27) \end{matrix}$

	Figure Option View Download New Window
	图10 例2所求FOPD控制器参数K_p和μ Fig.10 K_pversus μ with FOPD controller in case 2

可以得到系统开环传递函数伯德图以及系统开环增益变化10%的系统阶跃响应图(见图11)。

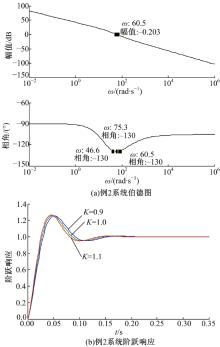	Figure Option View Download New Window
	图11 例2所求系统开环传递函数伯德图和阶跃响应Fig.11 Bode plot and unit step responses with designed FOPD controller in case 2

例3 被控对象P(s)= $\begin{matrix} \frac{1}{s (Ts + 1)} \end{matrix}$ , 其中T=0.05 s, 穿越频率ω _c=45 rad/s, 相位裕度φ _m=70° 。

由图12可得在穿越频率处被控对象的模值为-40.8 dB, 相角为-156° 。由式(6)可得到被控对象的角速度 $\begin{matrix} {φ_{P}|}_{ω = 45} \end{matrix}$ =-8.2474× 10^-³。运用Matlab求解程序, 可得FOPD控制器参数K_p=63.15, μ =0.8959(见图13), K_d=2.6403, 进而得控制器传递函数为:

$\begin{matrix} C_{3} (s) = 63.15 + 2.6403 s^{0.8959} (28) \end{matrix}$

	Figure Option View Download New Window
	图12 被控对象P(s)在45 rad/s的模值和相位Fig.12 Plant’ s amplitude and phase in the 45 rad/s

	Figure Option View Download New Window
	图13 例3所求FOPD控制器参数K_p和μ Fig.13 K_p versus μ with FOPD controller in case 3

可以得到系统开环传递函数伯德图以及系统开环增益变化10%的系统阶跃响应图(见图14)。

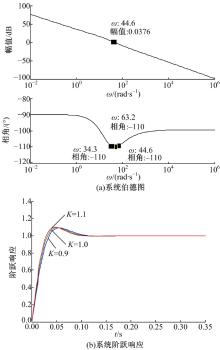	Figure Option View Download New Window
	图14 例3所求系统开环传递函数伯德图和阶跃响应Fig.14 Bode plot and unit step responses with designed FOPD controller in Case3

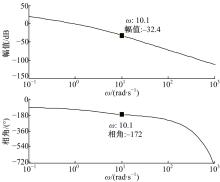
例4 被控对象T(s)= $\begin{matrix} \frac{1}{s (Ts + 1)} \end{matrix}$ e^-ts, 其中T=0.4, t=0.01。穿越频率ω _c=10 rad/s, 相位裕度φ _m=50° 。

由图15可得在穿越频率处被控对象的模值为-32.5 dB, 相角为-172° 。由式(6)可得到被控对象的角速度 $\begin{matrix} {φ_{T}|}_{ω = 10} \end{matrix}$ =-0.033 53。运用求解程序可得FOPD控制器参数K_p=24.75, μ =0.8539(见图16), K_d=4.0564, 进而得控制器传递函数为:

$\begin{matrix} C_{4} (s) = 24.75 + 4.0564 s^{0.8539} (29) \end{matrix}$

	Figure Option View Download New Window
	图15 被控对象T(s)在10 rad/s的模值和相位Fig.15 Plant’ s amplitude and phase in the 10 rad/s

	Figure Option View Download New Window
	图16 例4所求FOPD控制器参数K_p和μ Fig.16 K_pversus μ with FOPD controller in case 4

可以得到系统开环传递函数伯德图以及系统开环增益变化10%的系统阶跃响应图(见图17)。

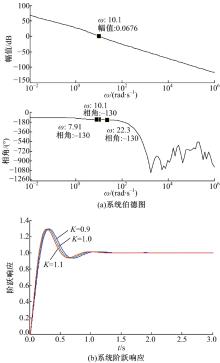	Figure Option View Download New Window
	图17 例4所求系统开环传递函数伯德图和阶跃响应Fig.17 Bode plot and unit step responses with designed FOPD controller in case4

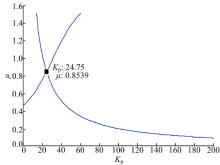
由图9(a)、11(a)、14(a)和17(a)可知基于向量方法的增益鲁棒FOPD控制器Matlab程序求解参数能满足控制系统开环伯德图在穿越频率处的相位是平坦的频率特性设计要求, 从图9(b)、11(b)、14(b)和17(b)阶跃响应可知, 基于向量的增益鲁棒FOPD控制器方法设计的FOPD控制器能够满足在开环增益变化± 10%的阶跃响应超调量几乎不变的增益鲁棒性条件。由图8、图10、图13和图16可看出基于向量的FOPD控制器Matlab程序求解参数算法的解是唯一的。

对比不同相位裕度(例1和例2)、不同穿越频率(例1和例3)和不同被控对象(例1和例4)条件下的FOPD控制器参数求解过程, 采用基于向量的鲁棒FOPD控制器参数求解算法程序有效并可快速地求解FOPD控制器参数。

7 结束语

提出了基于向量的增益鲁棒性FOPD控制器参数求解简化算法, 可以快速地求解FOPD控制器参数。相比于文献[8-11], 基于向量的增益鲁棒分数阶比例微分控制器参数计算方法不仅推导过程简单, 而且计算量小。同时可以程序化求解在不同被控对象条件下的增益鲁棒性分数阶控制器参数。结果表明, 基于向量的的鲁棒分数阶PD控制器参数求解算法是有效的。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	金永顺. 面向鲁棒运动控制系统的分数阶PID控制器设计、自整定及实验研究[D]. 长沙: 湖南大学电气与信息工程学院, 2011. Jin Yong-shun, Fractional order PID controller synthesis, auto-tuning and experiment studies for robust motion control systems[D]. Changsha: College of Electrical and Information Engineering, Hunan University, 2011. [本文引用:2]
[2]	Chen Y Q, Dou H F, Vinagre B M, et al. A robust tuning method for fractional order PI controllers[DB/OL]. [2014-03-26]. http://mechatronics.ece.usu.edu/yqchen/paper/06C11_We-AE-1_1FDA06082.pdf. [本文引用:2]
[3]	Chen Y Q, Ahn H S, Igor P. Robust stability check of fractional order linear time invariant systems with interval uncertainties[J]. Signal Processing, 2006, 86(10): 2611-2618. [本文引用:1]
[4]	Chen Yang-quan, Ahn Hyo-sung, Xue Ding-yü. Robust controllability of interval fractional order linear time invariant systems[J]. Signal Processing, 2006, 86(10): 2794-2802. [本文引用:1]
[5]	Ahn Hyo-sung, Chen Yang-quan. Necessary and sufficient stability condition of fractional-order interval linear systems[J]. Automatica, 2008, 44(11): 2985-2988. [本文引用:1]
[6]	Ahn Hyo-sung, Chen Yang-quan. Conservatism free robust stability check of fractional order interval linear systems[C]∥Proeeeding of the 17th IFAC World Congress, USA, 2008: 15256-15261. [本文引用:1]
[7]	Luo Ying, Chen Yang-quan. Stabilizing and robust fractional order PI controller synthesis for first order plus time delay systems[J]. Automatica, 2012, 48(9): 2159-2167. [本文引用:1]
[8]	Luo Ying, Chen Yang-quan, Wang Chun-yang, et al. Tuning fractional order proportional integral controllers for fractional order systems[J]. Journal of Process Control, 2010, 20(7): 823-831. [本文引用:1]
[9]	Luo Ying, Li Hong-sheng, Chen Yang-quan. Fractional order proportional and derivative controller synthesis for a class of fractional order systems: Tuning rule and hardware-in-the-loop experiment[C]∥Proceedings of the 48th IEEE Conference on Decision and Control, Shanghai, China, 2009: 5460-5465. [本文引用:1]
[10]	Li Hong-sheng, Luo Ying, Chen Yang-quan. A fractional order proportional and derivative (FOPD) motion controller: tuning rule and experiments[J]. IEEE Transactions on Control Systems Technology, 2010, 18(2): 516-520. [本文引用:1]
[11]	Li Hong-sheng, Chen Yang-quan. A fractional order proportional and derivative (FOPD) controller tuning algorithm[C]∥Control and Decision Conference, Yantai, Shand ong, 2008: 4059-4063. [本文引用:1]