基于改进最小二乘算法的船舶操纵性参数辨识

引用本文

秦余钢, 马勇, 张亮, 李腾飞. 基于改进最小二乘算法的船舶操纵性参数辨识.吉林大学学报:工学版, 2016, 46(3): 897-903
QIN Yu-gang, MA Yong, ZHANG Liang, LI Teng-fei. Parameter identification of ship's maneuvering motion based on improved least square method. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 897-903 复制到剪切板

Permissions

基于改进最小二乘算法的船舶操纵性参数辨识

秦余钢, 马勇, 张亮, 李腾飞

哈尔滨工程大学船舶工程学院,哈尔滨 150001

通讯作者:马勇(1980-),男,讲师,博士.研究方向:海洋潮流能利用.E-mail:mayong02@hrbeu.edu.cn

作者简介:秦余钢(1981-),男,博士研究生.研究方向:计算流体力学.E-mail:qinyugang@hrbeu.edu.cn

基金:国家自然科学基金项目(51309069); 中央高校基本科研业务费项目(HEUCF150106)

摘要

为了解决船舶操纵性参数辨识问题,考虑了船舶运动时域的非线性和非平稳的特点,提出了一种快速收敛迭代学习最小二乘算法,提高了参数辨识速度和精度。首先建立了船舶操纵一阶和二阶非线性运动响应模型,并将其离散化;然后采用迭代学习思想,并引入P型学习率改进了递推最小二乘算法进行参数辨识;同时分析了该算法的收敛性;最后进行了相关实验。实验结果证明了该算法的可行性和有效性。

关键词: 计算机应用; 最小二乘法; 参数辨识; 迭代学习; 船舶操纵性; 响应模型

中图分类号:U661,TP391 文献标志码:A 文章编号:1671-5497(2016)03-0897-07

Parameter identification of ship's maneuvering motion based on improved least square method

QIN Yu-gang, MA Yong, ZHANG Liang, LI Teng-fei

College of Shipbuilding Engineering,Harbin Engineering University, Harbin 150001,China

Abstract

In order to solve the problem of parameter identification of ship's maneuvering motion, a fast convergent iterative least square algorithm is presented, in which the nonlinear and non-stationary characteristics of the ship motion in time domain are taken into consideration. First, the first-order and second-order nonlinear response motion of the ship are estimated and discretized. Then, the parameters are identified using the proposed least square algorithm, which is improved by using iterative learning and introducing p-type learning rate. The convergence of the algorithm is also analyzed. Simulation experiments are conducted and results show that the speed and precision of parameter identification are improved using this algorithm. This demonstrates that the proposed algorithm is feasible and effective.

Keyword: computer application; least square method; parameter identification; interactive learning; ship maneuvering; response model

Show Figures

0 引言

船舶操纵性是船舶水动力性能研究的重点之一, 关系到船舶航行的安全问题。经过近30年的发展, 船舶操纵性研究越来越被人们所重视, 出现以“ 船舶操纵性暂行标准” 和“ 正式标准” 为代表的重大成果。该标准是国际海事组织(International maritime organization, IMO)征询了各成员国的建议后, 先后于1993年和2002年颁布^[1]。标准对船舶设计阶段的操纵性预报以及船舶应满足的操纵性指标提出了明确的定量要求, 极大地促进了船舶操纵性预报研究。通过建立船舶操纵运动仿真系统在船舶设计阶段进行操纵性预报和评估是最实用和有效的方法^[2]。该方法需要对船舶的运动模型进行数学建模, 而确定数学模型中众多的水动力导数则是建模的关键。

目前, 利用系统辨识的方法来确定水动力导数是最简单有效的方法之一。而最小二乘法则是系统辨识中最基本的方法^[3], 它具有系统先验统计知识少、算法简单、计算量少、收敛性好等特点。特别是递推最小二乘法避免了矩阵求逆的运算, 实现了参数在线辨识。但是在辨识的精度和速度上还可以继续提高。而迭代学习方法采用“ 在重复中学习” 的策略^[4], 具有记忆系统和经验修正机制, 使递推最小二乘算法具有了某种智能^{[5, 6]}。它可以从过去的系统输入输出和参数估计中获得额外的信息, 并不断训练辨识器, 为改进参数估计提供了可能性, 使辨识效果越来越好。

本文从基础最小二乘法出发, 采用迭代学习的思想, 同时在迭代学习的过程中加入了P型学习率^[7], 以提高其收敛的速度和辨识精度, 完成了基于快速收敛迭代学习最小二乘算法的非线性船舶操纵性参数的在线辨识。仿真实验结果证明了该方法的有效性。

1 船舶操纵运动模型的建立

目前, 经过理论分析和实践检验的船舶操纵运动模型主要有两类^{[8, 9, 10]}:一类是水动力模型; 另一类是响应模型。考虑到船舶操纵性参数尽量少, 同时兼顾其可观测性, 采用经典的KT方程作为船舶数学模型。该模型中包含 $\begin{matrix} K 、 T \end{matrix}$ 等操纵性指数, 这些指数可由一些线性水动力导数求得。

一阶非线性响应模型^[11]:

$\begin{matrix} T \overset{\cdot}{r} + r + α r^{3} = Kδ \end{matrix}$ (1)

式中: $\begin{matrix} r \end{matrix}$ 为转艏角速度; $\begin{matrix} δ \end{matrix}$ 为舵角; $\begin{matrix} K 、 T \end{matrix}$ 为操纵性指数; $\begin{matrix} α \end{matrix}$ 为非线性项系数。

二阶非线性响应模型为:

$\begin{matrix} T_{1} T_{2} \overset{\cdot \cdot}{r} + (T_{1} + T_{2}) \overset{\cdot}{r} + r + α r^{3} = Kδ + K T_{3} \overset{\cdot}{δ} \end{matrix}$ (2)

式中: $\begin{matrix} K, T_{1}, T_{2} \end{matrix}$ 和 $\begin{matrix} T_{3} \end{matrix}$ 是操纵性指数, $\begin{matrix} α \end{matrix}$ 是非线性项系数。

将式(1)前向差分离散化可得

$\begin{matrix} r (t + 1) = a_{1} r (t) + a_{2} r^{3} (t) + b_{1} δ (t) + ε (t) \end{matrix}$ (3)

式中: $\begin{matrix} t \end{matrix}$ 为时间节拍; $\begin{matrix} ε (t) \end{matrix}$ 为高斯白噪声; $\begin{matrix} a_{1} 、 a_{2} \end{matrix}$ 和b₁为待辨识的系数项, 它们与一阶非线性船舶操纵性指数的关系为:

$\begin{matrix} \{\begin{matrix} T = (1 - a_{1} \frac{)}{Δ} t \\ α = - a_{2} T / Δt \\ K = b_{1} T / Δt \end{matrix} \end{matrix}$ (4)

式中: $\begin{matrix} Δt \end{matrix}$ 为采样间隔。

令 $\begin{matrix} T_{1} T_{2} = h, T_{1} + T_{2} = g, \end{matrix}$ 则对式(2)前向差分离散化可得:

$\begin{matrix} \begin{matrix} r (t + 1) = a_{1} r (t) + a_{2} r (t - 1) + a_{3} r^{3} (t - 1) + \\ b_{1} δ (t) + b_{2} δ (t - 1) + ε (t) \end{matrix} \end{matrix}$ (5)

式中: $\begin{matrix} a_{1} 、 a_{2} 、 a_{3} 、 b_{1} \end{matrix}$ 和 $\begin{matrix} b_{2} \end{matrix}$ 为待辨识的系数项, 它们与二阶非线性船舶操纵性指数的关系为:

$\begin{matrix} \{\begin{matrix} h = Δ t^{2} / (1 - a_{1} - a_{2}) \\ g = (2 - a_{1}) h / Δt \\ α = - a_{3} h \\ K = (b_{2} + b_{1}) h / Δ t^{2} \\ T_{3} = b_{1} h / (KΔt) \end{matrix} \end{matrix}$ (6)

船舶操纵性参数辨识的问题就是已知船舶运动状态序列 $\begin{matrix} r (t) \end{matrix}$ 和 $\begin{matrix} δ (t), t = 1, 2, 3, \dots, N, \end{matrix}$ 求解 $\begin{matrix} a_{1} 、 a_{2} 、 a_{3} 、 b_{1} \end{matrix}$ 和 $\begin{matrix} b_{2}, \end{matrix}$ 进而计算非线性船舶操纵性指数 $\begin{matrix} K 、 T 、 T_{1} 、 T_{2} 、 T_{3} \end{matrix}$ 和 $\begin{matrix} α 。 \end{matrix}$

令 $\begin{matrix} y^{Ι} (t) = r (t + 1), φ^{Ι} (t) = [r (t), r^{3} (t), δ {(t)]}^{T}, θ^{Ι} = [a_{1}, a_{2}, b_{1}]^{T}, \end{matrix}$ 则式(3)可化为:

$\begin{matrix} y^{Ι} (t) = {φ^{Ι}}^{T} (t) θ^{Ι} + ε (t) \end{matrix}$ (7)

令 $\begin{matrix} y^{ΙΙ} (t) = r (t + 1), φ^{ΙΙ} (t) = [r (t), r (t - 1), r^{3} (t - 1), δ (t), δ {(t - 1)]}^{T}, θ^{ΙΙ} = [a_{1}, a_{2}, a_{3}, b_{1}, b_{2}]^{T}, \end{matrix}$ 则式(5)可以化简为:

$\begin{matrix} y^{ΙΙ} (t) = {φ^{ΙΙ}}^{T} (t) θ^{ΙΙ} + ε (t) \end{matrix}$ (8)

2 快速收敛迭代学习最小二乘算法

2.1 标准递推最小二乘法

可以用以下模型表示式(7)和(8)两个系统:

$\begin{matrix} y (t) = φ^{T} (t) θ + ε (t) \end{matrix}$ (9)

最小二乘法的原理就是寻求未知向量 $\begin{matrix} θ \end{matrix}$ 的估计值 $\begin{matrix} \hat{θ} (t), \end{matrix}$ 使其极小化模型残差平方和^{[12, 13]}:

$\begin{matrix} J = \overset{N}{\sum_{t = 1}} e^{2} (t) \end{matrix}$ (10)

式中: $\begin{matrix} e (t) = y (t) - φ^{T} (t) \hat{θ} (t) 。 \end{matrix}$

令 $\begin{matrix} Y (t) = [y (1), y (2), \dots, y {(t)]}^{T}, Φ (t) = [φ (1), φ (2), \dots, φ {(t)]}^{T}, \end{matrix}$ 则性能指标 $\begin{matrix} J \end{matrix}$ 可以写成:

$\begin{matrix} J = [Y (t) - Φ^{T} (t) \hat{δ} {(t)]}^{T} [Y (t) - Φ^{T} (t) \hat{δ} (t)] \end{matrix}$ (11)

可以得到基于到时刻 $\begin{matrix} t \end{matrix}$ 的观测 $\begin{matrix} δ \end{matrix}$ 的非递推最小二乘估值为:

$\begin{matrix} \hat{δ} (t) = [Φ {(t)}^{T} Φ {(t)]}^{- 1} Φ^{T} (t) Y (t) \end{matrix}$ (12)

为了消除可能存在分母为零的情况, 避免矩阵求逆的运算, 可得递推增益最小二乘估值为^[14]:

$\hat{δ} (t + 1) = \hat{δ} (t) + \frac{P (t) φ (t + 1) [y (t + 1) - φ^{T} (t + 1) \hat{δ} (t)]}{1 + φ^{T} (t + 1) P (t) φ (t + 1)}$ (13)

$P (t + 1) = P (t) + \frac{[P (t) φ (t + 1)] [P (t) φ {(t + 1)]}^{T}}{1 + φ^{T} (t + 1) P (t) φ (t + 1)}$ (14)

式中:P(t)为协方差矩阵, 初值 $\begin{matrix} \hat{δ} \end{matrix}$ (0)=0, P(0)=γ I。γ 为非常大的正数。且规定 $\begin{matrix} r (t) = 0, δ (t) = 0, t \leq 0 。 \end{matrix}$

2.2 快速收敛迭代学习最小二乘法

在 $\begin{matrix} t \end{matrix}$ 时刻, 由式(9)可以得到:

$\begin{matrix} y (t) = φ^{T} (t) \hat{θ} (t) + e (t) \end{matrix}$ (15)

经过 $\begin{matrix} k \end{matrix}$ 次迭代有:

$\begin{matrix} y_{k} (t) = {φ_{k}}^{T} (t) {\hat{θ}}_{k} (t) + e_{k} (t) \end{matrix}$ (16)

令 $\begin{matrix} e_{k} (t) = y_{k} (t) - {φ_{k}}^{T} (t) {\hat{θ}}_{k} (t), Y_{k} (t) = [y_{1} (t), y_{2} (t), \dots, y_{k} {(t)]}^{T}, Φ_{k} (t) = [φ_{1} (t), φ_{2} (t), \dots, φ_{k} {(t)]}^{T}, Ω_{k} (t) = [e_{1} (t), e_{2} (t), \dots, e_{k} {(t)]}^{T}, \end{matrix}$ 则有:

$\begin{matrix} Y_{k} (t) = {Φ_{k}}^{T} (t) {\hat{θ}}_{k} (t) + Ω_{k} (t) \end{matrix}$ (17)

考虑下述指标函数:

$\begin{matrix} \begin{matrix} J_{k} ({\hat{θ}}_{k} (t)) = \\ \frac{1}{2} [Y_{k} (t) - Φ_{k} (t) {\hat{θ}}_{k} {(t)]}^{T} [Y_{k} (t) - Φ_{k} (t) {\hat{θ}}_{k} (t)] \end{matrix} \end{matrix}$ (18)

类似递推最小二乘算法有:

${\hat{θ}}_{k}^{LS} (t) = {\hat{θ}}_{k - 1} (t) + \frac{P_{k - 1} (t) φ_{k} (t)}{1 + {φ_{k}}^{T} (t) P_{k - 1} (t) φ_{k} (t)} e_{k} (t)$ (19)

式中：

$P_{k} (t) = P_{k - 1} (t) - \frac{P_{k - 1} (t) φ_{k} (t) {φ_{k}}^{T} (t) {P^{T}}_{k - 1} (t)}{1 + {φ_{k}}^{T} (t) P_{k - 1} (t) φ_{k} (t)}$ (20)

初值为：

$\{\begin{matrix} P_{0} (t) = P (t - 1) \\ {\hat{θ}}_{0} (t) = \hat{θ} (t - 1) \end{matrix}$ (21)

经过 $\begin{matrix} N \end{matrix}$ 次迭代, 达到了迭代终止条件, 则有:

$\begin{matrix} \{\begin{matrix} P (t) = P_{N} (t) \\ \hat{θ} (t) = {\hat{θ}}_{N} (t) \end{matrix} \end{matrix}$ (22)

一般迭代的终止条件为:

$\begin{matrix} \{\begin{matrix} ‖ {\hat{θ}}_{k + 1} (t) - {\hat{θ}}_{k} (t) ‖ < σ \\ else \\ k = Nmax \end{matrix} \end{matrix}$ (23)

式中: $\begin{matrix} σ \end{matrix}$ 为一个小正数, $\begin{matrix} Nmax \end{matrix}$ 为设定的迭代最大次数。

为了加快收敛速度, 增加了P型迭代项。即:

$\begin{matrix} {\hat{θ}}_{k} (t) = {\hat{θ}}^{LS} k_{(} t) + β φ_{k} (t) {\hat{e}}_{k} (t) \end{matrix}$ (24)

式中: $\begin{matrix} β \end{matrix}$ 为P型迭代系数, $\begin{matrix} {\hat{e}}_{k} (t) = y_{k} (t) - {φ_{k}}^{T} (t) {\hat{θ}}_{k}^{LS} (t) 。 \end{matrix}$

由上可知, 快速收敛迭代学习最小二乘辨识算法的基本步骤如下:

步骤1 对于时刻 $\begin{matrix} t, \end{matrix}$ 根据式(21)给定初始值 $\begin{matrix} P_{0} (t), {\hat{θ}}_{0} (t), \end{matrix}$ 并设置 $\begin{matrix} k = 0 。 \end{matrix}$

步骤2 第 $\begin{matrix} k \end{matrix}$ 次重复运行时, 依照式(20)(24)更新 $\begin{matrix} P_{k} (t) \end{matrix}$ 和 $\begin{matrix} {\hat{θ}}_{k} (t) 。 \end{matrix}$

步骤3 根据式(23)检验迭代学习终止条件, 如果满足条件则转步骤(4), 否则, $\begin{matrix} k = k + 1, \end{matrix}$ 转步骤(2)。

步骤4 根据公式(22)更新 $\begin{matrix} \hat{θ} (t) \end{matrix}$ 和 $\begin{matrix} P (t), t = t + 1, \end{matrix}$ 转步骤1。

2.3 收敛性分析

令 $\begin{matrix} {\tilde{θ}}_{k} (t) = {\hat{θ}}_{k} (t) - θ, \end{matrix}$ 则:

$\begin{matrix} \begin{matrix} {\tilde{θ}}_{k} (t) - {\tilde{θ}}_{k - 1} (t) = {\hat{θ}}_{k} (t) - {\hat{θ}}_{k - 1} (t) = \\ \frac{P_{k - 1} (t) φ_{k} (t)}{1 + {φ_{k}}^{T} (t) P_{k - 1} (t) φ_{k} (t)} e_{k} (t) + β φ_{k} (t) {\hat{e}}_{k} (t) \end{matrix} \end{matrix}$ (25)

令 $\begin{matrix} χ (t) = \frac{1}{1 + {φ_{k}}^{T} (t) P_{k - 1} (t) φ_{k} (t)}, \end{matrix}$

由式(19)可得:

$P_{k} (t) φ_{k} (t) = χ_{k} (t) P_{k - 1} (t) φ_{k} (t)$ (26)

而：

$e_{k} (t) = y_{k} (t) - {φ_{k}}^{T} (t) {\hat{θ}}_{k - 1} (t) = - {φ_{k}}^{T} (t) {\tilde{θ}}_{k - 1} (t)$ (27)

${\hat{e}}_{k} (t) = - χ_{k} (t) {φ^{T}}_{k} (t) {\tilde{θ}}_{k - 1} (t)$ (28)

将式(27)(28)带入(25)得:

$\begin{matrix} \begin{matrix} {\tilde{θ}}_{k} (t) = \\ P_{k} (t) P_{k - 1}^{- 1} (t) {\tilde{θ}}_{k - 1} (t) - β χ_{k} (t) φ_{k} (t) {φ_{k}}^{T} (t) {\tilde{θ}}_{k - 1} (t) \end{matrix} \end{matrix}$ (29)

定义Lyapunov函数:

$V_{k} (t) = {\tilde{θ}}^{T}_{k} (t) P_{k}^{- 1} (t) {\tilde{θ}}_{k} (t)$ (30)

则：

$V_{k} (t) - V_{k - 1} (t) = {θ^{T}}_{k} (t) P_{k}^{- 1} (t) {\tilde{θ}}_{k} (t) - {θ^{T}}_{k - 1} (t) P_{k - 1}^{- 1} (t) {\tilde{θ}}_{k - 1} (t) = A + B$ (31)

$A = - χ_{k} (t) {\tilde{θ}}^{T}_{k - 1} (t) φ_{k} (t) {φ_{k}}^{T} (t) {\tilde{θ}}_{k - 1} (t)$ (32)

$B = - β χ_{k}^{2} (t) {\tilde{θ}}^{T}_{k - 1} (t) φ_{k} (t) {φ_{k}}^{T} (t) {2 P_{k}^{- 1} - 1 (t) + [2 I - β P_{k}^{- 1} (t)] φ_{k} (t) {φ_{k}}^{T} (t)} {\tilde{θ}}_{k - 1} (t)$ (33)

由式(32)可知 $\begin{matrix} A \leq 0 。 \end{matrix}$ 只要 $\begin{matrix} B \leq 0, \end{matrix}$ 就可以根据Lyapunov定律证明该算法的收敛性。

由式(20)可知:

$\begin{matrix} 0 < λ_{(P_{k} (t))} < λ_{(P_{k - 1} (t))} < \dots < λ_{(P_{0} (t))} < λ_{(P (0))} = γ \end{matrix}$ (34)

$\begin{matrix} λ \end{matrix}$ 为 $\begin{matrix} P_{k} (t) \end{matrix}$ 的最大特征值。则

$\begin{matrix} \begin{matrix} B < - β χ_{k}^{2} (t) {θ^{T}}_{k - 1} (t) φ_{k} (t) {φ_{k}}^{T} (t) {2 P_{k - 1}^{- 1} (t) + \\ [2- β γ^{- 1}] φ_{k} (t) {φ_{k}}^{T} (t)} {\tilde{θ}}_{k - 1} (t) \end{matrix} \end{matrix}$ (35)

如果 $\begin{matrix} β \leq 2 γ, 则 B < 0, \end{matrix}$ 即:

$V_{k} (t) - V_{k - 1} (t) = A + B < 0$ (36)

由于 $\begin{matrix} γ \end{matrix}$ 为非常大的正数, 所以条件 $\begin{matrix} 0 < β \leq 2 γ \end{matrix}$ 很容易满足, 则不等式(36)是成立的。从而证明该迭代学习最小二乘法是收敛的。

3 实验及结果分析

3.1 仿真实验

根据文献^[15]对某型船舶进行数值模拟。分别进行了一阶非线性和二阶非线性模型的5° /10° Z型仿真实验。在仿真实验中, 船舶的响应模型采用4阶龙格库塔法进行积分^[16], 采样的时间间隔为0.1。为了模拟真实情况, 在模型中添加了高斯白噪声, 白噪声的均值为0, 方差为0.05。一阶非线性响应模型的初始值为 $\begin{matrix} K = 0, T = 0 \end{matrix}$ 和 $\begin{matrix} α = 0 \end{matrix}$ , 二阶非线性模型的初始值为 $\begin{matrix} K = 1, g = 0.2, h = 0.01, T_{3} = 0 \end{matrix}$ 和 $\begin{matrix} α = 0 。 \end{matrix}$ 在实验中分别采用了递推最小二乘法和快速收敛迭代学习最小二乘法对未知参数进行辨识。其中快速收敛迭代学习最小二乘法的最大迭代步数 $\begin{matrix} Nmax = 200; β = 0.005; \end{matrix}$ 极小值 $\begin{matrix} σ = 0.001; γ = 10^{6} 。 \end{matrix}$ 仿真对比实验结果如表1和表2所示, 各个辨识参数的历程曲线如图1和图2所示。

表1 一阶非线性仿真实验数据记录表 Table 1 Data of the first order nonlinear simulation experiment

	设定值	基础最小二乘法		快速收敛迭代学习最小二乘法
	设定值	辨识值	误差	辨识值	误差
$\begin{matrix} K \end{matrix}$	0.216	0.2182	0.0022	0.2175	0.0015
$\begin{matrix} T \end{matrix}$	13.514	13.647	0.133	13.598	0.084
$\begin{matrix} α \end{matrix}$	258.405	260.394	1.989	256.738	-1.667

表1 一阶非线性仿真实验数据记录表 Table 1 Data of the first order nonlinear simulation experiment

表2 二阶非线性仿真实验数据记录表 Table 2 Data of the second order nonlinear simulation experiment

	设定值	基础最小二乘法		迭代学习最小二乘法
	设定值	辨识值	误差	辨识值	误差
$\begin{matrix} h \end{matrix}$	8.045	8.483	-0.438	8.065	-0.02
$\begin{matrix} g \end{matrix}$	16.136	16.527	-0.391	15.838	0.298
$\begin{matrix} α \end{matrix}$	98.14	98.65	-0.51	98.12	0.02
T₃	0.312	0.323	-0.011	0.304	0.008

表2 二阶非线性仿真实验数据记录表 Table 2 Data of the second order nonlinear simulation experiment

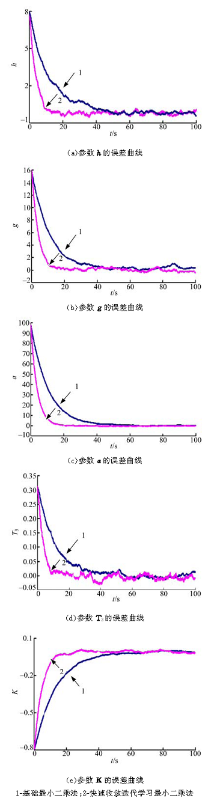
由表1可知, 基础最小二乘法和快速收敛迭代学习最小二乘法均能辨识出船舶一阶非线性操纵运动参数。对于 $\begin{matrix} K \end{matrix}$ 的辨识误差分别为0.0022和0.0015, 两者几乎一致。但是对于 $\begin{matrix} T 和 α \end{matrix}$ 的辨识误差差距较大, 快速收敛迭代学习最小二乘法要稍微优于基础最小二乘法。由图1可知, 采用基础最小二乘算法辨识时, 在第60 s的时候才能收敛到真实值附近, 而快速收敛迭代最小二乘法辨识时, 在不到20 s就已经收敛到真实值附近, 证明了其快速收敛的特性。

	Figure Option View Download New Window
	图1 一阶非线性模型参数的误差曲线Fig.1 Error curves for the first order nonlinear model parameters

	Figure Option View Download New Window
	图2 二阶非线性模型参数的误差曲线Fig.2 Error curves for the first order nonlinear model parameters

由表2可知, 基础最小二乘法和快速收敛迭代学习最小二乘法均能辨识出船舶二阶非线性操纵运动参数。K与T₃ 的辨识误差几乎一致。但是对于g、h和α 的辨识误差差距较大, 快速收敛迭代学习最小二乘法要明显优于基础最小二乘法。由图2可知, 采用基础最小二乘算法辨识时, 在60 s之后才能收敛到真实值附近, 而采用快速收敛迭代最小二乘法辨识时, 在20 s左右就可以收敛到真实值附近, 证明了其快速收敛的特性。

3.2 水池实验

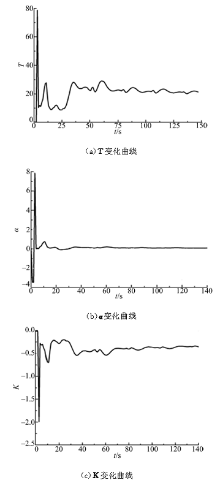
KVLCC1已被作为国际上验证和确认船舶操纵性预报方法的基准船型。本文实验数据来自在德国汉堡水池(HSVA)进行的自航模实验。该实验中船模在静水、深水中进行。文献^[17]介绍了船模的基本参数。实验的相关参数为直航速度U₀=1.179 m/s, 螺旋桨转速n=10.23 (1/s), 船首尾无吃水差, 操舵速率为 $\begin{matrix} {\overset{\cdot}{δ}}_{R} \end{matrix}$ =15.8° /s。

采用快速收敛迭代学习最小二乘法对其一阶非线性响应模型进行辨识, 船模进行15° /5° Z形实验。其模型的初始值为 $\begin{matrix} K = 0, T = 0 \end{matrix}$ 和 $\begin{matrix} α = 0, \end{matrix}$ 最大迭代步数为N_max=50, $\begin{matrix} β = 0.01 \end{matrix}$ , 极小值 $\begin{matrix} σ = 0.01, γ = 10^{3} 。 \end{matrix}$ 相关参数的历程曲线如图3所示。

	Figure Option View Download New Window
	图3 参数辨识历程曲线Fig.3 Course curves of parameter identification

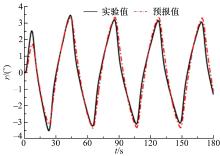
在完成了上述参数辨识后, 进行了25° /5° Z形实验操纵性能预报实验, 结果如图4所示。

	Figure Option View Download New Window
	图4 艏向角速度预报图Fig.4 Forecast of the heading angular velocity

由图4可知, 通过该算法辨识的相关操纵性参数可以很好地预报船舶的相关操纵性性能。

综上所述, 相对于基础最小二乘法来说, 快速收敛迭代学习最小二乘法在收敛速度和辨识精度方面都有所提高, 采用迭代学习方法可以改善基础最小二乘法的性能。快速收敛迭代学习最小二乘法能够更好更快地辨识船舶非线性操纵运动参数。

同时由于采用了迭代学习的思想, 因而其计算量成倍加大, 在设定最大迭代步数为200次的条件下, 现有的计算机是能够在有限的时间内完成计算量的。同时通过预报值与实际实验值的对比, 也证明了该算法的有效性。

4 结束语

提出了一种快速收敛迭代学习最小二乘算法, 用于解决船舶操纵性参数辨识问题。相对于基础最小二乘算法, 该算法的高效性源于采用了迭代学习方法, 使基础最小二乘算法具有了某种智能。仿真和实际实验表明, 快速收敛迭代学习最小二乘算法的收敛速度和辨识精度都有所提高, 该算法可行有效, 对船舶参数在线辨识具有重要意义。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	International Maritime Organization(IMO). Stand ards for Ship Maneuverability[S]. Resolution MSC, 2002137 (76). [本文引用:1]
[2]	罗伟林, 李铁山, 邹早建. 船舶操纵运动建模中的参数可辨识性问题[J]. 大连海事大学学报, 2009, 35(4): 1-3. Luo Wei-lin, Li Tie-shan, Zou Zao-jian. Parametric identifiability in modeling of ship maneuvering motion[J]. Journal of Dalian Maritime University, 2009, 35(4): 1-3. [本文引用:1]
[3]	孙明轩, 毕宏博. 学习辨识: 最小二乘算法及其重复一致性[J]. 自动化学报, 2012, 38(5): 698-706. Sun Ming-xuan, Bi Hong-bo. Learning identification: Least squares algorithms and their repetitive consistency[J]. Acta Automatica Sinica, 2012, 38(5): 698-706. [本文引用:1]
[4]	孙明轩, 黄宝健. 迭代学习控制[M]. 北京: 国防工业出版社, 1999. [本文引用:1]
[5]	王金海, 丁锋. CARMA模型离线最小二乘迭代辨识方法[J]. 科学技术与工程, 2007, 23(7): 5998-6002. Wang Jin-hai, Ding Feng. Least-square-iterative identification algorithm for CARMA models[J]. Science Technology and Engineering, 2007, 23(7): 5998-6002. [本文引用:1]
[6]	袁建国, 袁艳涛, 刘飞龙. MEMS陀螺仪的一种新颖高精度标定算法研究[J]. 重庆邮电大学学报: 自然科学版, 2014, 26(5): 666-669. Yuan Jian-guo, Yuan Yan-tao, Liu Fei-long. A novel high precision calibration algorithm for MEMS gyroscopes[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2014, 26(5): 666-669. [本文引用:1]
[7]	Palumbo P, Piroddi L. Harmonic analysis of non- linear structures by means of generalized frequency response functions coupled with NARX models[J]. Mechanical Systems and Signal Processing, 2000, 14(2): 243-265. [本文引用:1]
[8]	李必文. 线性广义系统的P型、PD型和PID型迭代学习控制[J]. 数学杂志, 2008, 28(6): 667-672. Li Bi-wen. Iteration learning control for linear singular Systems of P type, PD type and PID type[J]. Journal of Mathematics, 2008, 28(6): 667-672. [本文引用:1]
[9]	Korenberg M J, Billings S A, Liu Y P, et al. Orthogonal parameter estimation algorithm for non-linear stochastic systems[J]. International Journal of Control, 1988, 48(1): 193-210. [本文引用:1]
[10]	Billings S A, Korenberg M J, Chen S. Identification of non-linear output-affine systems using an orthogonal least square algorithm[J]. International Journal of Systems Science, 1988, 19: 1339-1568. [本文引用:1]
[11]	吴秀恒, 刘祖源. 船舶操纵性[M]. 北京: 国防工业出版社, 2005. [本文引用:1]
[12]	鲁铁定. 总体最小二乘的迭代解法[J]. 武汉大学学报: 信息科学版, 2010, 35(11): 1352-1353. Lu Tie-ding. An iterative algorithm for total least squares estimation[J]. Geomatics and Information Science of Wuhan University, 2010, 35(11): 1352-1353. [本文引用:1]
[13]	王徐华, 柏鹏, 李明阳, 等. 一种基于滑动最小二乘法的精确同步方法[J]. 重庆邮电大学学报: 自然科学版, 2013, 25(5): 599-604. Wang Xu-hua, Bai Peng, Li Ming-yang, et al. A precise synchronization method based on slipping least square algorithm[J]. Journal of Chongqing University of Posts and Telecommunications(Natural Science Edition), 2013, 25(5): 599-604. [本文引用:1]
[14]	王穗辉. 误差理论与测量平差[M]. 上海: 同济大学出版社, 2010. [本文引用:1]
[15]	张心光, 邹早建. 基于支持向量回归机的船舶操纵响应模型辨识[J]. 上海交通大学学报, 2011, 45(4): 501-504. Zhang Xin-guang, Zou Zao-jian. Identification of response models of ship maneuvering motion using support vector regression[J]. Journal of Shanghai Jiaotong University, 2011, 45(4): 501-504. [本文引用:1]
[16]	董国祥, 陆惠生, 江希龄. 船舶操纵运动仿真及其理论研究[J]. 上海交通大学学报, 1996, 30(10): 159-164, 170. Dong Guo-xiang, Lu Hui-sheng, Jiang Xi-ling. Simulation of ship maneuverability and its theoretical research[J]. Journal of Shanghai Jiaotong University, 1996, 30(10): 159-164, 170. [本文引用:1]
[17]	毕毅, 郭峰, 肖昌润, 等. 某特殊船型的操纵性模型实验研究[J]. 船舶工程, 2008, 30(2): 9-12. Bi Yi, Guo Feng, Xiao Chang-run, et al. Study on the model test of maneuverability of certain specific ship type[J]. Ship Engineering, 2008, 30(2): 9-12. [本文引用:1]

0.0

... 该标准是国际海事组织(International maritime organization,IMO)征询了各成员国的建议后,先后于1993年和2002年颁布^[1] ...

2009

0.0

. 2009, 35(4):1-3

Parametric identifiability in modeling of ship maneuvering motion

船舶操纵运动建模中的参数可辨识性问题

Luo Wei-lin , Li Tie-shan , Zou Zao-jian.

罗伟林, 李铁山, 邹早建

为保证系统辨识方法应用于船舶操纵运动建模中的有效性,提高建模精度,研究了船舶操纵运动辨识建模中的参数可辨识性问题.从系统辨识原理和船舶操纵运动数学模型结构特点的角度讨论了参数可辨识性的机理,并结合Mariner船试验数据,应用细长体理论分别计算了附加质量和黏性力导数,并与约束模试验结果进行对比.结果表明,附加质量的理论计算结果具有足够的精度,而黏性力导数的计算结果存在较大误差.为此,在应用系统辨识进行船舶操纵运动建模过程中,可将附加质量预先给定以解决参数可辨识性和提高辨识精度.

... 通过建立船舶操纵运动仿真系统在船舶设计阶段进行操纵性预报和评估是最实用和有效的方法^[2] ...

2012

0.0

. 2012, 38(5):698-706 DOI:doi:10.3724/SP.J.1004.2012.00698

Learning identification: Least squares algorithms and their repetitive consistency

学习辨识:最小二乘算法及其重复一致性

Sun Ming-xuan , Bi Hong-bo.

孙明轩, 毕宏博

This paper presents a learning identification method for stochastic systems with time-varying parametric uncertainties. The systems undertaken perform tasks repetitively over a pre-specified finite-time interval, and a least squares learning algorithm is derived on the basis of the repetitive operations. The learning identification method applies to periodically time-varying systems. It is shown that the estimates converge to the time-varying values of the parameters, and the complete estimation can be achieved under repetitive persistent excitation condition, a sufficient condition for establishing repetitive consistency of the learning algorithms. Numerical results are presented to demonstrate the effectiveness of the proposed learning algorithms.

针对重复时变系统, 提出学习辨识方法用于估计系统的时变参数. 讨论了有限时间作业区间上重复运行的时变系统以及周期时变系统两种情形. 文中给出最小二乘学习算法的推导过程, 并分析了所提算法的收敛性. 结果表明, 当重复持续激励条件成立时, 提出的学习算法具有重复一致性, 能够给出时变参数的完全估计. 通过数值算例进一步验证了学习算法的有效性.

... 而最小二乘法则是系统辨识中最基本的方法^[3],它具有系统先验统计知识少、算法简单、计算量少、收敛性好等特点 ...

1999

0.0

... 的策略^[4],具有记忆系统和经验修正机制,使递推最小二乘算法具有了某种智能^[5,6] ...

2007

0.0

. 2007, 23(7):5998-6002 DOI:doi:10.3969/j.issn.1671-1815.2007.23.006

Least-square-iterative identification algorithm for CARMA models

CARMA模型离线最小二乘迭代辨识方法

Wang Jin-hai , Ding Feng.

王金海, 丁锋

Based on the iterative least squares principle, two least-squares-iterative algorithms are developed for CARMA models and output error models. These two iterative algorithms use all measured input-output data at each iteration, and thus have highly accurate parameter estimation and faster convergence rates than the recursive extended least squares algorithm and auxiliary model based recursive least squares algorithm, respectively. The basic idea is to adopt the interactive estimation theory and hierarchical identification principle, the parameter estimates rely on the noise estimates, and the noise estimates are computed by the preceding parameter estimates. This performs a hierarchical computation processes. Finally, the simulation results indicate that the proposed algorithm can produce high accurate parameter estimation.

基于迭代最小二乘原理,提出了辨识CARMA模型和输出误差模型参数的最小迭代算法。两个最小二乘迭代算法分别比递推增广最小二乘算法和辅助模型递推算法具有更高的参数精度和具有很快的收敛速度。最小二乘迭代辨识的基本思想是:采用交互估计理论和递阶辨识原理,在每步迭代计算中,参数估计依赖于噪声估计,反过来噪声估计通过前一次迭代的参数估计计算,二者执行了一个递阶计算过程。最后用仿真例子验证了提出的算法。

... 的策略^[4],具有记忆系统和经验修正机制,使递推最小二乘算法具有了某种智能^[5,6] ...

2014

0.0

. 2014, 26(5):666-669 DOI:doi:10.3979/j.issn.1673-825X.2014.05.018

A novel high precision calibration algorithm for MEMS gyroscopes

MEMS陀螺仪的一种新颖高精度标定算法研究

Yuan Jian-guo , Yuan Yan-tao , Liu Fei-long.

袁建国, 袁艳涛, 刘飞龙

为了提高微机电系统(microelectro mechanical systems,MEMS)陀螺仪的测量精度,分析了MEMS陀螺仪的静态误差,建立了MEMS陀螺仪的输出模型和标定原理,提出了一种新颖的加权递推最小二乘标定算法,该算法可对MEMS陀螺仪进行高精度的标定,并对低精度MEMS陀螺仪给出了有效自适应滤波处理方法。通过大量实验数据分析表明,利用提出的标定算法,误差补偿后的MEMS陀螺仪性能得到了显著的提高。

... 的策略^[4],具有记忆系统和经验修正机制,使递推最小二乘算法具有了某种智能^[5,6] ...

2000

0.0

... 本文从基础最小二乘法出发,采用迭代学习的思想,同时在迭代学习的过程中加入了P型学习率^[7],以提高其收敛的速度和辨识精度,完成了基于快速收敛迭代学习最小二乘算法的非线性船舶操纵性参数的在线辨识 ...

2008

0.0

. 2008, 28(6):667-672

Iteration learning control for linear singular Systems of P type, PD type and PID type

线性广义系统的P型、PD型和PID型迭代学习控制

Li Bi-wen.

李必文

本文研究了线性定常广义系统在P型、PD型和PID型学习律作用下的迭代控制问题,利用矩阵理论和微分不等式方法,得到了其迭代控制收敛性结果.不仅对于时变系统也成立,而且,可以移植到线性定常广义离散时间系统.

... 1 船舶操纵运动模型的建立目前,经过理论分析和实践检验的船舶操纵运动模型主要有两类^[8,9,10]:一类是水动力模型 ...

1988

0.0

... 1 船舶操纵运动模型的建立目前,经过理论分析和实践检验的船舶操纵运动模型主要有两类^[8,9,10]:一类是水动力模型 ...

1988

0.0

... 1 船舶操纵运动模型的建立目前,经过理论分析和实践检验的船舶操纵运动模型主要有两类^[8,9,10]:一类是水动力模型 ...

2005

0.0

... 一阶非线性响应模型^[11]: ...

2010

0.0

. 2010, 35(11):1352-1353 DOI:doi:10.3969/j.issn.1000-1158.2012.05.20

An iterative algorithm for total least squares estimation

总体最小二乘的迭代解法

Lu Tie-ding.

鲁铁定

针对总体最小二乘解算问题,应用测量平差中的间接平差原理推导了总体最小二乘的迭代逼近解算公式,通过与奇异值分解法进行比较,得出两种解算方法具有等价性。实验数据分析验证了算法的有效性。

... 最小二乘法的原理就是寻求未知向量 θ的估计值 θ^(t),使其极小化模型残差平方和^[12,13]: ...

2013

0.0

. 2013, 25(5):599-604 DOI:doi:10.3979/j.issn.1673-825X.2013.05.007

A precise synchronization method based on slipping least square algorithm

一种基于滑动最小二乘法的精确同步方法

Wang Xu-hua , Bai Peng , Li Ming-yang

王徐华, 柏鹏, 李明阳

最小二乘拟合鉴相曲线的方法可以实现精确同步,但其只能工作在很小的误差范围内,适用范围窄.提出一种基于正斜率和误差平方和最小准则的滑动最小二乘精确同步方法,该方法在粗同步前后各一个码片范围内进行滑动搜索选出最优测量结果.分析和仿真结果表明,该方法具有很强的抗噪声能力,并且在粗同步误差较大时依然具有很高的测量精度.

... 最小二乘法的原理就是寻求未知向量 θ的估计值 θ^(t),使其极小化模型残差平方和^[12,13]: ...

2010

0.0

... 为了消除可能存在分母为零的情况,避免矩阵求逆的运算,可得递推增益最小二乘估值为^[14]: ...

2011

0.0

. 2011, 45(4):501-504

Identification of response models of ship maneuvering motion using support vector regression

基于支持向量回归机的船舶操纵响应模型辨识

Zhang Xin-guang , Zou Zao-jian.

张心光, 邹早建

Abstract： By applying the LSsupport vector regression to analyze the data of rudder angle and yaw rate obtained from the deformed zigzag test of freerunning model, the manoeuvrability indexes in the response models of ship manoeuvring motion were identified. The obtained response models were solved numerically by RungeKutta method to simulate the deformed zigzag manoeuvres. The prediction results of heading angle and yaw rate were compared with the test data to verify the proposed method. Key words： ship manoeuvring; response model; parameter identification; support vector regression

通过对自航模变形Z形试验舵角与转艏角速度数据的分析，应用最小二乘支持向量回归机（Least SquareSupport Vector Regression，LSSVR）辨识了船舶操纵运动响应模型中的操纵性指数，并用回归得到的响应模型进行了变形Z形试验的数值模拟.通过将首向角和转艏角速度的预报结果与自航模试验数据进行比较，结果验证了该方法的有效性.

... 1 仿真实验根据文献^[15]对某型船舶进行数值模拟 ...

1996

0.0

. 1996, 30(10):159-164,170

Simulation of ship maneuverability and its theoretical research

船舶操纵运动仿真及其理论研究

Dong Guo-xiang , Lu Hui-sheng , Jiang Xi-ling.

董国祥, 陆惠生, 江希龄

建立了船舶操纵运动仿真数学模型，给出了一种新的风力和风力矩数学模型并预报了船舶在风作用下的操纵运动，提出了估算浅水中船体水动力的新方法，预报了船舶在浅水中的操纵性能，研究了边界元理论在船体水动力计算中的应用，并利用理论计算结果，预报了船舶的回转运动及Ｚ形操纵．

... 在仿真实验中,船舶的响应模型采用4阶龙格库塔法进行积分^[16],采样的时间间隔为0 ...

2008

0.0

. 2008, 30(2):9-12 DOI:doi:10.3969/j.issn.1000-6982.2008.02.003

Study on the model test of maneuverability of certain specific ship type

某特殊船型的操纵性模型实验研究

Bi Yi , Guo Feng , Xiao Chang-run

毕毅, 郭峰, 肖昌润

通过在露天操纵性水池里,对某一自带一个长度约为2/3水线长坞舱的特殊船型自航模进行的回转、Z形和航向稳定性试验,研究了这类船型的操纵性能,特别研究了湿坞是否导致船操纵性能的恶化.作者分别对自航模在干坞和湿坞两种不同状态下进行了对比性试验.研究结果表明湿坞状态自航模回转性能和航向稳定性均优于干坞状态.

... 文献^[17]介绍了船模的基本参数 ...