汽车电子稳定控制系统的分层控制策略及试验

引用本文

靳立强, 刘刚, 陈鹏飞. 汽车电子稳定控制系统的分层控制策略及试验. 吉林大学学报:工学版, 2016, 46(6): 1765-1771
JIN Li-qiang, LIU Gang, CHEN Peng-fei. Hierarchical control for vehicle electronic stability control system. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 1765-1771 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606002
Permissions

汽车电子稳定控制系统的分层控制策略及试验

靳立强¹, 刘刚^1,², 陈鹏飞¹

1.吉林大学汽车仿真与控制国家重点实验室, 长春 130022

2.河南工学院自动控制系,河南新乡 453000

作者简介:靳立强(1976-),男,教授,博士生导师.研究方向:汽车底盘电子控制技术,电动汽车四轮独立驱动技术.E-mail:jinlq@jlu.edu.cn

基金项目:国家自然科学基金项目(50907030); 中国博士后科学基金项目(2013M54024B)

摘要

为了提高车辆在复杂工况下的稳定性能,设计了基于分层控制的电子稳定控制系统(ESC)。系统的上层控制器以横摆角速度和质心侧偏角为控制变量,采用模糊PID算法计算出车辆维持稳定所需的横摆力矩;下层控制器根据上层输出的所需横摆力矩计算得出被控车轮的滑移率变化量,然后采用变参数PID算法对车轮进行滑移率控制,从而实现车辆所需的横摆力矩。最后,应用Matlab/Simulink验证了该控制算法的有效性,并将该算法移植到单片机做冬季实车场地试验,单移线和双移线工况试验结果表明了该算法的工程实用性。

关键词: 车辆工程; 电子稳定控制系统; 模糊PID控制; 横摆力矩控制

中图分类号:U461 文献标志码:A 文章编号:1671-5497(2016)06-1765-07

Hierarchical control for vehicle electronic stability control system

JIN Li-qiang¹, LIU Gang^1,², CHEN Peng-fei¹

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

2.Department of Automation, Henan Institute of Technology, Xinxiang 453000, China

Abstract

In order to improve the vehicle stability under complex working condition, an electronic stability control system based on hierarchical strategy is proposed. The up layer of the controller is a fuzzy Proportional-integral-derivative (PID) controller, and the controlling variables are the yaw rate and the side-slip angle. The desired yaw moment is calculated by the upper layer. The target slip rate is calculated based on the relationship between the yaw moment and the slip rate. Then, the lower layer is applied to control the slip rate. Finally, the ESC algorithm is verified by Matlab/Simulink. The winter road test shows that the proposed control strategy can improve vehicle stability performance.

Key words: vehicle engineering; electronic stability control(ESC); fuzzy-PID; yaw moment control

Show Figures

0 引言

电子稳定控制系统(Electronic stability control, ESC)是通过主动控制横摆力矩避免车辆在高速转向出现不足转向或者转向过度等危险工况^{[1, 2, 3, 4]}。目前针对ESC的研究多采用现代控制理论的方法。文献[5]采用模型预测控制的方法设计了ESC控制器, 并设计了基于二次规划的横摆力矩分配方法, 仿真结果显示该方法使得车辆能够有效跟踪期望运动轨迹。文献[6]利用最优控制理论计算出系统所需横摆力矩, 再通过基于模糊控制算法的变滑移率算法实现力矩分配, 仿真结果有效地证明了算法的可靠性。文献[7]利用滑模变结构控制理论, 以横摆角速度、质心侧偏角及二者联合作为控制变量实现电子稳定控制, 仿真结果表明联合控制变量的方式有效地提高了车辆操纵稳定性。文献[8]采用LQR理论加前馈控制的方法计算出目标横摆力矩, 再根据轮胎力模型实现横摆力矩的分配, 硬件在环仿真结果显示该方法实时性较好。文献[9]在分析了人-车闭环系统的动力学模型后, 以质心侧偏角为控制变量, 分别采用前馈和神经PID两种控制算法, 通过仿真比较证明神经PID算法优于前馈控制。文献[2, 10]采用终端滑模控制算法实现了轮毂电动车的稳定性控制, 终端滑模控制具有较好的抗干扰性能, 但系统在抖动方面需要注意。

本文利用动力学模型对质心侧偏角进行估计, 通过分层控制策略设计电子稳定控制系统的上、下层控制器, 采用仿真分析验证ESC算法的可靠性。并根据V字开发流程, 将算法移植至单片机进行冬季场地实车试验, 通过实车试验结果对ESC算法进行了评价。

1 整车模型

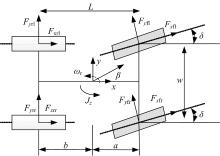
车辆模型采用7自由度整车模型进行动力学仿真, 如图1所示。车辆模型能够有效地反映车辆在纵向、侧向以及横摆等方向的动力学特征。模型的动力学方程如下。

纵向动力学方程:

$\begin{matrix} m ({\overset{\cdot}{V}}_{x} - ω_{r} V_{y}) = (F_{xfl} + F_{xfr}) cosδ - (F_{yfl} + F_{yfr}) + F_{xrl} + F_{xrr} \end{matrix}$ (1)

侧向动力学方程:

$\begin{matrix} m ({\overset{\cdot}{V}}_{y} - ω_{r} V_{x}) = (F_{xfl} + F_{yfr}) sinδ - (F_{yfl} + F_{yfr}) + F_{yrl} + F_{yrr} \end{matrix}$ (2)

横摆动力学方程:

$\begin{matrix} J_{z} {\overset{\cdot}{ω}}_{r} = a (F_{xfl} + F_{yfr}) sinδ + a (F_{yfl} + F_{yfr}) cosδ - b (F_{yrl} + F_{yrr}) + \frac{w}{2} sinδ + M_{yaw} \end{matrix}$ (3)

式中:m为车辆质量; a、b分别为前、后轴到质心的距离; w为左、右两轮之间的宽度; V_x、V_y分别为车辆的纵向和侧向速度; ω _r为横摆角速度; F_x、F_y分别为车辆所受的纵向力和侧向力; δ 为车辆前轮侧偏角, 可通过方向盘转角传感器的测量值转换得到; J_z为车辆绕z轴的转动惯量; M_yaw为车辆ESC系统介入控制时的横摆力矩。

	Figure Option View Download New Window
	图1 七自由度车辆模型Fig.1 7 DoF vehicle model

2 ESC分层控制策略

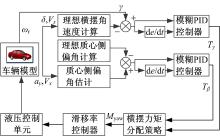
整个车辆ESC系统采用了分层控制的方法, 将系统分成了上层和下层控制器, 结构如图2所示。图2中, a_y为车辆侧向加速度; v_x为车辆纵向车速; δ 为车辆前轮转角; T_γ为基于横摆角速度模糊控制器输出的制动力矩; T_β为基于质心侧偏角模糊控制器的制动力矩。上层控制器部分根据车辆的偏航率传感器(能够测量横摆角速度、纵向加速度和侧向加速度)、方向盘转角传感器的测量值计算当前工况下车辆的理想横摆角、理想质心侧偏角以及质心侧偏角的估算值, 再计算理想横摆角速度和实际横摆角速度的差值Δ ω _r及理想质心侧偏角和质心侧偏角的差值Δ β 。根据Δ ω _r和Δ β 采用模糊PID算法计算得到车辆期望横摆力矩。下层控制器根据横摆力矩分配策略选择车轮进行力矩分配, 再根据车轮所得横摆力矩计算得到车轮的目标滑移率, 通过对滑移率控制, 最终实现车辆的电子稳定控制功能。

	Figure Option View Download New Window
	图2 控制结构图Fig.2 Schematic of control structure

3 上层控制器设计

3.1 理想横摆角速度和理想质心侧偏角计算

在计算理想横摆角速度、理想质心侧偏角以及估计质心侧偏角时, 采用做等速圆周运动的线性二自由度车辆模型进行计算。根据阿克曼方程, 可以求得车辆的理想横摆角速度:

$\begin{matrix} ω_{rd} = \frac{V_{x}}{L (1 + K V_{x}^{2})} δ \end{matrix}$ (4)

式中:ω _rd为车辆在做等速圆周运动时的横摆角速度, 即理想横摆角速度; c_r和c_f分别为前、后车轮的侧偏刚度; 稳定性因数K为:

$\begin{matrix} K = \frac{m}{L^{2}} (\frac{a}{c_{r}} - \frac{b}{c_{f}}) \end{matrix}$ (5)

由于侧向加速度受到路面附着的限制以及路面附着系数采用的是估计值, 所以对横摆角速度上限值进行修正:

$\begin{matrix} ω_{r_{upper}} = \min \{| ω_{rd} |, 0.9 \frac{μg}{V_{x}}\} sgnδ \end{matrix}$ (6)

考虑到模型的瞬态响应特性, 增加一阶滞后环节增强理想横摆角速度计算的准确性, 最终得到:

$\begin{matrix} {\overset{\cdot}{ω}}_{r} = \frac{1}{1 + τs} ω_{r_{upper}} \end{matrix}$ (7)

式中:τ 为目标响应时间。

根据二自由度车辆模型做等速圆周运动的情况, 在稳态时 $\begin{matrix} \overset{\cdot}{β} \end{matrix}$ =0, 可得理想质心侧偏角:

$\begin{matrix} β_{d} = \frac{b / L + ma V_{x}^{2} / (L^{2} c_{r})}{1 + K V_{x}^{2}} δ \end{matrix}$ (8)

根据文献[11]对车辆理想质心侧偏角的上限进行限制:

$\begin{matrix} β_{upper} = \min \{β_{d}, \arctan (0.02 μg)\} \end{matrix}$ (9)

同样, 由于瞬态响应特性, 增加一阶滞后环节, 最终得到车辆理想质心侧偏角为:

$\begin{matrix} β = \frac{1}{1 + τs} β_{upper} (10) \end{matrix}$

3.2 质心侧偏角估算

质心侧偏角是车辆稳定性控制中一个重要的参数, 在车辆上很少采用直接测量的方式, 因为直接测量质心侧偏角的成本较昂贵, 且该类传感器在复杂的行驶工况下易受干扰。目前大多数文献采用非线性卡尔曼滤波、观测器等算法进行质心侧偏角估算, 但由于算法耗时较长, 较少在ESC系统中使用。本文采用了基于偏航率传感器的质心侧偏角估算方法。

车辆质心侧偏角的公式为:

$\begin{matrix} β = \arctan \frac{V_{y}}{V_{x}} \end{matrix}$ (11)

车辆在行驶过程中质心侧偏角β 较小, 根据三角函数定理, 式(11)可以改写为:

$\begin{matrix} β = \arctan \frac{V_{y}}{V_{x}} \approx \frac{V_{y}}{V_{x}} \end{matrix}$ (12)

在ESC系统中, 车辆的质心侧偏角在每个10 ms程序运行周期就需要估算一次。因此车辆的纵向速度在10 ms内可以看成是一个常量。接着对式(12)微分可得:

$\begin{matrix} \overset{\cdot}{β} = \frac{d}{dt} (\frac{V_{y}}{V_{x}}) \approx \frac{{\overset{\cdot}{V}}_{y}}{V_{x}} \end{matrix}$ (13)

由线性二自由度汽车模型的运动微分方程可得:

$\begin{matrix} a_{y} = {\overset{\cdot}{V}}_{y} + ω_{r} V_{x} \end{matrix}$ (14)

将式(14)代入式(13)可得:

$\begin{matrix} \overset{\cdot}{β} = \frac{a_{y}}{V_{x}} - ω_{r} \end{matrix}$ (15)

最后对式(16)求积分即可得到车辆当前的质心侧偏角估计值为:

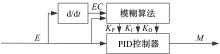
$\begin{matrix} β = \sum (\frac{a_{y}}{V_{x}} - ω_{r}) Δt \end{matrix}$ (16)

3.3 控制器设计

本文设计的ESC控制程序运行时间大约为1 ms, 每40 ms就需要运行一次ESC部分控制程序, 因此在上层控制器算法设计方面采用实时性较强的模糊PID控制算法。控制器的控制参数有两个, 分别是横摆角速度和质心侧偏角。当偏航率传感器测量得到的横摆角速度值超出横摆角速度门限值时, 控制器采用基于横摆角速度的模糊PID算法; 而当质心侧偏角超出门限值时, 控制器则在下一个40 ms程序周期切换至基于质心侧偏角的模糊PID算法。

	Figure Option View Download New Window
	图3 模糊PID控制结构图Fig.3 Control structure of fuzzy PID

基于横摆角速度的模糊PID控制算法与基于质心侧偏角的算法结构类似, 如图3所示, 模糊PID控制根据输入的变量E及变量变化率EC的值, 对PID的三个参数进行在线调节, 满足不同路况下ESC的控制需求。模糊PID控制的输入和输出的语言变量模糊集设置为[NB(负大), NM(负中), NS(负小), Z(零), PS(正小), PM(正中), PB(正大)]; 基于横摆角速度的模糊PID控制算法的输入信号分别为Δ ω _r和Δ $\begin{matrix} {\overset{\cdot}{ω}}_{r} \end{matrix}$ , 其论域分别为[-0.15, 0.15]和[-1, 1]; 基于质心侧偏角的模糊PID控制算法的输入信号分别为Δ β 和Δ $\begin{matrix} \overset{\cdot}{β} \end{matrix}$ , 其论域分别为[-5° , 5° ]和[-1, 1]; PID的3个系数K_P、K_I、K_D的论域分别为[0, 1000], [0, 1], [1, 10]。通过制定模糊规则、解模糊等步骤, 上层控制器的期望输出横摆力矩表达式为:

$\begin{matrix} \begin{matrix} ΔM = φ (K_{P 1} Δ ω_{r} + K_{I 1} \sum ω_{r} Δt + K_{D 1} Δ ω_{r} Δt) + \\ (1 - φ) (K_{P 2} Δβ + K_{I 2} \sum βΔt + K_{D 2} ΔβΔt) (17) \end{matrix} \end{matrix}$

4 下层控制策略

在整个ESC控制系统中, 实现上层控制器计算得到的横摆力矩分配是下层控制器的主要任务。横摆力矩分配首选需要先考虑制动车轮的选取问题, 文献[11, 12]采用优化理论求出制动力分配到4个车轮上的最优解, 这类分配策略较复杂, 常用于装有轮毂电机的电动车。采用单轮控制则不需要考虑4轮控制时力矩配合的问题, 简单易实现。制动车轮则采取业内认可的经验:车辆右转转向不足时, 优先控制内侧后轮; 车辆右转转向过度时, 则优先控制外侧前轮。在下层控制器算法方面选择滑移率控制的方法。

ESC在采用滑移率控制时分两步, 首先要根据上层控制器计算得到的横摆力矩的大小来确定被控车轮的滑移率变化量; 然后采用可变参数自适应PID算法实现对制动车轮的控制。

以右转转向过度为例, 需要对外侧前轮施加横摆力矩, 根据文献[8]可知, 横摆力矩与滑移率变化之间的关系为:

$\begin{matrix} \begin{matrix} ΔM = \sqrt[]{{(\frac{T}{2})}^{2} + b^{2}} \cdot \cos (\arctan \frac{2 a}{T} - δ) \cdot \\ \frac{d F_{xfl}}{d λ_{o}} (λ_{d} - λ_{o}) - \sqrt[]{{(\frac{T}{2})}^{2} + a^{2}} \cdot \\ \sin (\arctan \frac{2 a}{T} - δ) \cdot \frac{d F_{yfl}}{d λ_{o}} (λ_{d} - λ_{o}) \cdot \frac{d F_{yfl}}{d λ_{o}} Δλ \end{matrix} \end{matrix}$ (18)

式中:Δ M为实现ESC控制所需横摆力矩变化量; λ _o为ESC介入控制前的滑移率; λ _d为实现横摆力控制所对应的目标滑移率。

目标滑移率与车轮当前滑移率的偏差e(k)=λ _d(k)-λ (k), 采用增量PID计算得到主动制动压力的变化率为:

$\begin{matrix} Δp (k) = K_{P} Δe (k) + K_{I} e (k) + K_{D} [Δ e (k) - Δe (k - 1)] (19) \end{matrix}$

式中:比例系数K_P、积分系数K_I及微分系数K_D的大小根据e(k)进行选取, 如表1所示, 表1中E₁=0.2, E₂=0.5。

表1 PID参数 Table 1 Parameters of PID

5 仿真及场地试验

5.1 仿真试验

为了验证ESC算法的性能, 采用Matlab/Simulink软件做了仿真试验, 分析比较了有、无ESC控制器下车辆的相应特性。车辆参数如表2所示。仿真工况为车辆速度80 km/h, 路面附着系数为0.3, 转向角输入0.25 rad的阶跃信号。

表2 某乘用车技术参数 Table 2 Technical parameters of vehicle

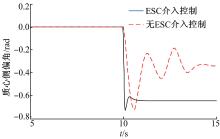
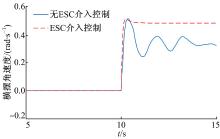
图4为车辆在有ESC控制介入和无介入情况下的横摆角速度对比, 在无ESC控制介入的情况下, 车辆的横摆角速度出现震荡, 此时车辆处于失稳的状态。在ESC控制介入的情况下, 车辆的横摆角速度收敛逐渐达到稳定状态。图5为车辆在有ESC控制介入和无介入情况下质心侧偏角对比, 无ESC介入情况下, 车辆质心侧偏角发散震荡, 此时车辆处于失稳工况。而在ESC控制下, 车辆横摆角速度能够紧密地跟随目标值。

	Figure Option View Download New Window
	图4 横摆角速度对比Fig.4 Comparison of yaw rate

	Figure Option View Download New Window
	图5 质心侧偏角对比Fig.5 Comparison of side-slip angle

5.2 冬季场地试验

2015年2月在黑河某试车场参照ISO 3888-1:1999(E)标准进行了低附着场地试验, 试验车型为国产乘用车。试验场地及控制器安装如图6所示。车辆上安装了轮速传感器、方向盘转角传感器、偏航率传感器。ESC控制器及其电磁阀的电子部件安装在装有主缸压力传感器的液压单元上。试验数据由CANalyzer CAN总线数据分析仪获得。

	Figure Option View Download New Window
	图6 控制器及试验场地Fig.6 ECU and test site

	Figure Option View Download New Window
	图7 低附着单移线试验结果Fig.7 Vehicle in single-lane test with control under low mue surface

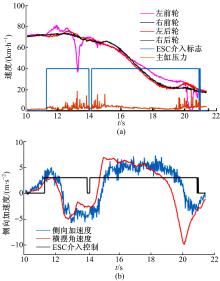
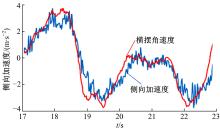
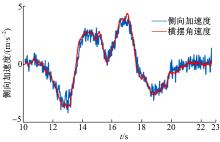
首先进行的是在冰雪路面(附着系数约为0.3~0.35)下的单移线试验, 场地布置参考ISO 3888-1:1999(E)标准。图7为此次试验所记录的轮速、主缸压力、侧向加速度以及横摆角速度等信息。由图7(a)可见, 车辆的初始速度为70 km/h, 进入场地后, 车辆挂空挡滑行, 在右转过程中出现转向过度情况时, ESC控制器对左前轮进行主动制动控制调整车辆行驶状态。在20 s时, 车辆左转时过度转向, ESC控制器对右前轮进行主动制动控制。整个过程刹车踏板信号始终为0, 从主缸压力曲线可以观察到, ESC介入控制前压力值为0; ESC介入控制后, 液压单元依靠电机以电磁阀实现主动增压来对车轮进行制动。由图7(b)可以观察到车辆的侧向加速度和横摆角速度变化趋势相同, 与车辆转向角变化保持一致; 从图7(b)可见, 侧向加速度的峰值为7.31 m/s², 横摆角速度的峰值为44.2 (° )/s。图8为车辆在关闭ESC功能后成功通过单移线工况的试验数据, 可见侧向加速度的峰值仅为3.8 m/s², 横摆角速度的峰值为11.3 (° )/s。

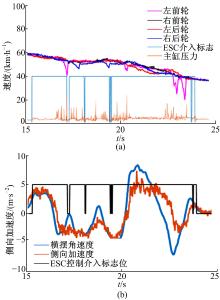
	Figure Option View Download New Window
	图8 无ESC控制介入单移线工况试验结果Fig.8 Results of vehicle in single-lane test without control

图9为冰雪路面双移线试验的试验数据图。由ESC控制介入标志曲线可知, ESC在试验过程中多次启动维持车辆稳定性。在ESC控制介入后, 通过主动制动的方式对单个车轮进行控制, 且车辆的侧向加速度和横摆角速度趋势一致。从图9(b)可见, 侧向加速度的峰值为7.3 m/s², 横摆角速度的峰值为41.88 (° )/s。图10为同等初速度60 km/s下, 关闭ESC功能后车辆成功通过双移线工况的试验结果, 侧向加速度的峰值为4.23 m/s², 横摆角速度的峰值为17.54 (° )/s。在开启ESC功能后, 车辆的峰值侧向加速度提高了70%, 横摆角速度峰值更是大幅度提高, 说明ESC功能极大地提高了车辆在危险工况下的安全性能。

	Figure Option View Download New Window
	图9 低附着双移线试验结果Fig.9 Vehicle in double-lane test with control under low mue surface

	Figure Option View Download New Window
	图10 无ESC控制介入双移线工况试验结果Fig.10 Results of vehicle in double-lane test without control

6 结束语

针对传统乘用车设计了电子稳定控制算法, 采用分层控制思想分别设计了上、下层控制器及质心侧偏角参数估计算法。通过仿真验证了算法的可靠性, 并在冬季进行了低附着单移线和双移线工况的实车试验。通过对比开启和关闭ESC功能后的试验数据可知, ESC功能提高了车辆低附着路面下的稳定性裕度, 改善了车辆在极限工况下的安全性能。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Xiong L, Yu Z, Wang Y, et al. Vehicle dynamics control of four in-wheel motor drive electric vehicle using gain scheduling based on tyre cornering stiffness estimation[J]. Vehicle System Dynamics, 2012, 50(6): 831-846. [本文引用:1]
[2]	Song P, Tomizuka M, Zong C. A novel integrated chassis controller for full drive-by-wire vehicles[J]. Vehicle System Dynamics, 2015, 53(2): 215-236. [本文引用:1]
[3]	Shuai Zhi-bin, Zhang Hui, Wang Jun-min, et al. Lateral motion control for four-wheel-independent-drive electric vehicles using optimal torque allocation and dynamic message priority scheduling[J]. Control Engineering Practice, 2014, 24: 55-66. [本文引用:1]
[4]	Shibahata Y, Shimada K, Tomari T. Improvement of vehicle maneuverability by direct yaw moment control[J]. Vehicle System Dynamics, 1993, 22(5): 465-481. [本文引用:1]
[5]	李刚, 宗长富, 陈国迎, 等. 线控转向四轮独立驱动电动车的AFS_DYC集成控制[J]. 华南理工大学学报, 2012, 40(3): 150-155. Li Gang, Zong Chang-fu, Chen Guo-ying, et al. Integrated AFS/DYC control of steering-by-wire 4WID electric vehicle[J]. Journal of South China University of Technology, 2012, 40(3): 150-155. [本文引用:1]
[6]	余卓平, 高晓杰, 张立军. 用于车辆稳定性控制的直接横摆力矩及车轮变滑移率联合控制研究[J]. 汽车工程, 2006, 28(9): 844-851. Yu Zhuo-ping, Gao Xiao-jie, Zhang Li-jun. A study on coordination of direct yaw monment control and variable wheel slip control for vehicle stability[J]. Automotive Engineering, 2006, 28(9): 844-851. [本文引用:1]
[7]	林程, 彭春雷, 曹万科. 独立驱动电动汽车稳定性的滑模变结构控制[J]. 汽车工程, 2015, 37(2): 132-138. Lin Cheng, Peng Chun-lei, Cao Wan-ke. Sliding mode variable structure control for the stability of independent drive electric vehicle[J]. Automotive Engineering, 2015, 37(2): 132-138. [本文引用:1]
[8]	Li L, Jia G, Chen J, et al. A novel vehicle dynamics stability control algorithm based on the hierarchical strategy with constrain of nonlinear tyre forces[J]. Vehicle System Dynamics, 2015, 53(8): 1093-1116. [本文引用:1]
[9]	宗长富, 郑宏宇, 田承伟, 等. 基于直接横摆力矩控制的汽车稳定性控制策略[J]. 吉林大学学报: 工学版, 2008, 38(5): 1010-1014. Zong Chang-fu, Zheng Hong-yu, Tian Cheng-wei, et al. Vehicle stability control strategy based on direct yaw moment control[J]. Journal of Jilin University(Engineering and Technology Edition), 2008, 38(5): 1010-1014. [本文引用:1]
[10]	Yang P. Stability control strategy design and experiment of distributed electric drive vehicle[J]. Journal of Mechanical Engineering, 2013, 49(24): 128-143. [本文引用:1]
[11]	玄圣夷, 宋传学, 靳立强. 基于多级鲁棒PID控制的汽车稳定性控制策略[J]. 吉林大学学报: 工学版, 2010, 40(1): 13-18. Xuan Sheng-yi, Song Chun-xue, Jin Li-qiang, et al. Multilevel robust PID control strategy for vehicle stability control[J]. Journal of Jilin University(Engineering and Technology Edition), 2010, 40(1): 13-18. [本文引用:1]
[12]	续丹, 王国栋, 曹秉刚, 等. 独立驱动电动汽车的转矩优化分配策略研究[J]. 西安交通大学学报, 2012, 46(3): 42-46. Xu Dan, Wang Guo-dong, Cao Bing-gang, et al. Study on optimaizing torque distribution strategy for independent 4WD electric vehicle[J]. Journal of Xi'an Jiaotong University, 2012, 46(3): 42-46. [本文引用:1]

2012

0.0

... 0 引言电子稳定控制系统(Electronic stability control,ESC)是通过主动控制横摆力矩避免车辆在高速转向出现不足转向或者转向过度等危险工况^[1,2,3,4] ...

2015

0.0

... 0 引言电子稳定控制系统(Electronic stability control,ESC)是通过主动控制横摆力矩避免车辆在高速转向出现不足转向或者转向过度等危险工况^[1,2,3,4] ...

2014

0.0

... 0 引言电子稳定控制系统(Electronic stability control,ESC)是通过主动控制横摆力矩避免车辆在高速转向出现不足转向或者转向过度等危险工况^[1,2,3,4] ...

1993

0.0

... 0 引言电子稳定控制系统(Electronic stability control,ESC)是通过主动控制横摆力矩避免车辆在高速转向出现不足转向或者转向过度等危险工况^[1,2,3,4] ...

2012

0.0

. 2012, 40(3):150-155 DOI:doi:10.3969/j.issn.1000-565X.2012.03.024

Integrated AFS/DYC control of steering-by-wire 4WID electric vehicle

线控转向四轮独立驱动电动车的AFS_DYC集成控制

Li Gang , Zong Chang-fu , Chen Guo-ying

李刚, 宗长富, 陈国迎

针对线控转向四轮独立驱动电动车的主动前轮转向( AFS)与直接横摆力矩控制(DYC)的集成控制问题,提出了一种基于模型预测控制的、采用分层集成控制结构的集成控制算法,设计了模型预测控制器,研究了基于二次规划的驱动力分配方法,并通过仿真实验对算法进行验证.结果表明:基于模型预测控制理论的集成控制算法能够使车辆有效地跟踪期望运动轨迹,提高车辆稳定性和主动安全性.

2006

0.0

. 2006, 28(9):844-851 DOI:doi:10.3321/j.issn:1000-680X.2006.09.013

A study on coordination of direct yaw monment control and variable wheel slip control for vehicle stability

用于车辆稳定性控制的直接横摆力矩及车轮变滑移率联合控制研究

Yu Zhuo-ping , Gao Xiao-jie , Zhang Li-jun.

余卓平, 高晓杰, 张立军

设计基于最优控制理论的横摆力矩控制策略和适用于复杂工况的制动力分配策略;设计基于模糊控制理论的滑移率分配算法并提出使横摆力矩控制和变滑移率控制协同工作的方法;最后通过转向盘的阶跃输入和正弦输入工况验证制动力分配策略的正确性和联合控制的有效性.

2015

0.0

. 2015, 37(2):132-138

Sliding mode variable structure control for the stability of independent drive electric vehicle

独立驱动电动汽车稳定性的滑模变结构控制

Lin Cheng , Peng Chun-lei , Cao Wan-ke.

林程, 彭春雷, 曹万科

摘　要：为充分利用双电机独立驱动电动汽车两侧电机独立可控这个特点来提高车辆稳定性,在研究汽车动力学与稳定性特点的基础上,利用MATLAB/Simulink建立了包括任意路径下的单点预瞄驾驶员模型和＂魔术公式＂轮胎模型在内的8自由度的＂人-车＂闭环动力学仿真平台。运用滑模变结构控制原理,分别设计了以两侧电机为执行机构,以横摆角速度、质心侧偏角和横摆角速度与质心侧偏角联合为控制变量的3种等速趋近滑模变结构控制器,在仿真平台进行了稳定性控制的仿真。结果表明,3种控制器均可有效提高汽车极端工况下的操纵稳定性,其中,又以横摆角速度与质心侧偏角为联合控制变量的控制器效果最好。

2015

0.0

2008

0.0

. 2008, 38(5):1010-1014

Vehicle stability control strategy based on direct yaw moment control

基于直接横摆力矩控制的汽车稳定性控制策略

Zong Chang-fu , Zheng Hong-yu , Tian Cheng-wei

宗长富, 郑宏宇, 田承伟

1.State Key Laboratory of Automobile Dynamics Simulation, Jilin University, Changchun 130022, China; 2.Institute of Automotive Engineering, Chang'an Automobile Holding Ltd.,Chongqing 401120, China

A vehicle dynamic model was established for the humanvehicle closeloop system to analyze the vehicle stability.Two direct yaw moment control(DYC) strategies,i.e.,the feedforward and single neuron PID control strategies were proposed to ensure the zero sideslip angle of the mass center.Through the simulation at low adhesion roads with double lane change,the two control strategies were compared.The seiulation results show that the single neuron DYC control strategy can more effectively control the wheel and vehicle motion,improve the lateral and longitudinal stability of the vehicle.

建立了适用于汽车稳定性分析的人车闭环系统整车动力学模型，提出了保证质心侧偏角为零的前馈和单神经元两种DYC控制策略。通过对这两种控制策略的低附着双移线道路仿真，对比分析了两种不同控制策略的控制效果。仿真结果表明：单神经元DYC控制策略能更有效地控制汽车运动状态，提高汽车纵向及侧向稳定性。

2013

0.0

2010

0.0

. 2010, 40(1):13-18

Multilevel robust PID control strategy for vehicle stability control

基于多级鲁棒PID控制的汽车稳定性控制策略

Xuan Sheng-yi , Song Chun-xue , Jin Li-qiang

玄圣夷, 宋传学, 靳立强

摘　要：利用AMESim软件搭建了整车和液压制动系统模型。将基于H∞控制理论的PID控制算法应用于汽车稳定性控制的研究。根据车辆行驶状态的变化调整鲁棒PID控制器的参数，构建以横摆角速度和质心侧偏角为控制目标的汽车稳定性控制算法。进而利用 PID控制算法得出制动轮缸压力，实现了整车的稳定性控制。利用Matlab／Simulink和AMESim建立联合仿真平台，对控制算法进行验证。结果表明，该控制算法具有很好的实时性和控制效果，能够满足车辆稳定性控制的要求。

2012

0.0

. 2012, 46(3):42-46

Study on optimaizing torque distribution strategy for independent 4WD electric vehicle

独立驱动电动汽车的转矩优化分配策略研究

Xu Dan , Wang Guo-dong , Cao Bing-gang

续丹, 王国栋, 曹秉刚

为了充分发挥四轮驱动电动汽车转矩独立可控的优势,提出了一种以提高驱动系统能效为目标的转矩分配策略.系统能效目标函数中包含了稳定性和经济性2个指标,旨在满足稳定行驶的同时尽量降低车辆的能量消耗.在横摆力矩、最大附着力和最大驱动力的约束条件下,对目标函数进行了求解,并利用MATLAB软件进行了仿真分析.结果表明,优化分配策略在保证车体稳定行驶的前提下,能够明显减少驱动系统的能量消耗,提高车体的系统能效.