考虑干线协调控制的城市最优路径搜索算法

引用本文

周熙阳, 杨兆升, 张伟, 邴其春, 商强. 考虑干线协调控制的城市最优路径搜索算法. 吉林大学学报:工学版, 2016, 46(6): 1799-1806
ZHOU Xi-yang, YANG Zhao-sheng, ZHANG Wei, BING Qi-chun, SHANG Qiang. Urban shortest path searching algorithm considering coordinate control of arterial intersections. Journal of Jilin University Engineering and Technology Edition, 2016, 46(6): 1799-1806 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb201606007
Permissions

考虑干线协调控制的城市最优路径搜索算法

周熙阳¹, 杨兆升^1,^2,³, 张伟^1,^2,⁴, 邴其春¹, 商强¹

1.吉林大学交通学院,长春 130022

2.吉林大学汽车仿真与控制国家重点实验室,长春 130022

3.吉林大学吉林省道路交通重点实验室,长春 130022

4.山东高速公路股份有限公司,济南 250014

张伟(1978-),男,高级工程师,在站博士后.研究方向:智能交通关键理论与技术.E-mail:z_wei@126.com

作者简介:周熙阳(1989-),男,博士研究生.研究方向:智能交通关键理论与技术.E-mail:zhouxy14@mails.jlu.edu.cn

基金项目:国家科技支撑计划项目(2014BAG03803)

摘要

针对现有最优路径搜索算法没有考虑到干线协调控制的情况,导致搜索到的最优路径实际效果不佳等问题,提出了一种考虑干线协调控制的城市最优路径搜索算法。首先,将相位差引入到干线协调配时方案中,提出了一种改进的信号交叉口等待时间模型。然后,以IDA^*算法为基础,提出了一种考虑干线协调控制的改进IDA^*搜索算法(AICIDA^*算法),以路径总时间费用和运算时间为评价指标进行了算例验证。结果表明:与传统算法和考虑干线协调控制的A^*算法(AICA^*算法)相比,AICIDA^*算法能够在更短的时间内搜索到费用更低的路径。

关键词: 交通运输系统工程; 最优路径搜索算法; 干线协调控制; 信号交叉口等待时间; IDA*算法

中图分类号:U491.1 文献标志码:A 文章编号:1671-5497(2016)06-1799-08

Urban shortest path searching algorithm considering coordinate control of arterial intersections

ZHOU Xi-yang¹, YANG Zhao-sheng^1,^2,³, ZHANG Wei^1,^2,⁴, BING Qi-chun¹, SHANG Qiang¹

1.College of Transportation, Jilin University, Changchun 130022, China

2.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022, China

3.Jilin Province Key Laboratory of Road Traffic, Jilin University, Changchun 130022, China, 4.Shandong High-speed Co., Ltd., Ji'nan 250014, China

Abstract

Existing shortest path searching algorithms do not consider the coordinate control of arterial intersections, which leads to unsatisfactory searching results. To overcome this drawback an urban shortest path algorithm is developed, which takes the coordinate control of arterial intersections into consideration. First, with the analysis of the coordinate signal timing at the arterial intersections and the offset parameter, an improved signal intersection waiting time model is proposed. Second, with the combination of IDA^* algorithm and the improved signal waiting time model, an improved IDA^* algorithm considering the coordinate control of arterial intersections (AICIDA^*) is developed. The AICIDA^* algorithm is compared with two traditional algorithms and an improved A^* algorithm considering the coordinate control of arterial intersections (AICA^*) through a case study, in which the path time cost and computing time are taken as the evaluation indexes. Results show that the proposed AICIDA^* algorithm can obtain the better path time cost in a shorter computing time.

Key words: engineering of communication and transportation system; shortest path searching algorithm; arterial intersections coordinate control; signal intersection waiting time; IDA* algorithm

Show Figures

0 引言

车辆最优路径搜索是智能交通诱导系统研究中的重要内容。城市路网不仅范围大, 且包含大量交通信息, 研究如何在实际城市路网中为车辆搜索到出行时间最短的路径, 对提高驾驶员出行效率具有重要意义。现有路径搜索算法主要包括标号法^{[1, 2, 3]}和启发式算法^{[4, 5, 6, 7, 8]}, 多数算法仅考虑路段行程时间, 忽略了车辆在交叉口处的等待时间, 导致所得最优路径实际效果不佳。

目前, 考虑信号交叉口等待时间的路径搜索算法主要有两类:①考虑交叉口平均信号延误。此类方法将延误模型叠加进路径搜索算法^{[9, 10, 11, 12]}, 或在路段划分时将交叉口作为路段的一部分, 将平均信号延误计入路段权重^[13]。此类方法建模简便, 但平均信号延误没有对单个车辆加以区分, 例如, 当驾驶员到达交叉口时遇到绿灯或红灯, 其实际等待时间具有较大差异, 对应的实际最优路径也会产生变化, 此类算法没有考虑这种差异, 所得路径与实际最优路径存在较大偏差。②根据车辆到达交叉口的时刻对单个车辆的信号交叉口等待时间进行建模, 此类方法考虑了当前相位状态, 计算车辆在不同相位离开时所需的等待时间, 与第一类方法相比更加贴合实际^[14]。但是, 该方法忽略了干线协调控制的情况, 干线协调是目前城市中广泛采用的控制方式, 不考虑干线协调配时将使等待时间的计算出现偏差, 进而影响所求最优路径的实际效果。

针对上述方法的缺陷, 本文提出了一种考虑干线协调控制的最优路径搜索算法。首先, 考虑干线协调配时, 对单车信号交叉口等待时间进行建模。然后, 以IDA^*算法为基础, 叠加等待时间模型, 提出一种考虑干线协调控制的改进IDA^*算法(AICIDA^*算法)。

1 考虑干线协调控制的信号交叉口等待时间模型

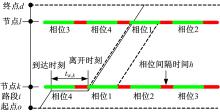
机动车在道路上行驶所产生的时间费用可划分为两大部分:一是在路段上行驶所消耗的时间; 二是在交叉口停车线前等待通行所消耗的时间。目前, 许多城市干线采用干线协调控制, 合理利用这些协调干线, 能够有效减少交叉口等待时间, 使机动车快速到达目的地。在图1所示的路径中, 机动车从起点o出发, 沿路段i驶往终点d, 节点k、l为干线协调控制交叉口, 协调相位为由南向北直行相位(均为相位1), 绿波带如虚线所示。当到达节点k时, 节点k的灯态为由南向西左转相位(相位4)绿灯, 相位1红灯。此时驾驶员有3种选择:①立即左转绕行; ②立即右转绕行; ③等待相位1绿灯, 等待时间为t_w,_k。驾驶员采用绕行可避免在当前交叉口等待, 但在绕行路线上可能消耗更多时间, 而选择直行, 虽然会在当前交叉口产生等待时间, 但可进入协调干线, 在节点l处等待时间为0, 直接驶向终点d。选择的路径不同, 路径上的信号交叉口等待时间也不同。

	Figure Option View Download New Window
	图1 路径选择示意图Fig.1 Schematic diagram of route choice

1.1 机动车到达相位判别

欲计算信号交叉口等待时间, 首先需要对机动车到达交叉口时交叉口所处的信号相位进行判别。

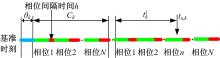
如图2所示, 设节点k参与信号协调控制, 绝对相位差为θ _k; 共有N个信号相位; 周期为C_k; 基准时刻为0时刻; 相位间隔时间为h; 机动车到达时刻为t_a,_k; 周期剩余时间为 $\begin{matrix} {t^{l}}_{k} \end{matrix}$ , 各参数满足如下关系:

$\begin{matrix} \{\begin{matrix} {t^{l}}_{k} = (t_{a, k} - θ_{k}) \mod C_{k} \\ s . t . t_{a, k} = t_{l, k (f)} + ω_{k (f), k} \\ t_{l, k (f)} = t_{a, k (f)} + t_{w, k (f)} \end{matrix} \end{matrix}$ (1)

式中:mod为取余运算符; t_a,_k₍_f₎、t_l,_k₍_f₎分别为机动车到达、离开上游节点k(f)的时刻; ω _k₍_f_),_k为有向路段k(f)k的行程时间; t_w,_k₍_f₎为机动车在上游节点k(f)的信号交叉口等待时间。

	Figure Option View Download New Window
	图2 到达相位判别Fig.2 Discrimination of arrival signal phase

由周期剩余时间 $\begin{matrix} {t^{l}}_{k} \end{matrix}$ 即可求得机动车的到达相位n:

$\begin{matrix} n = \{\begin{matrix} 1, 0 \leq {t^{l}}_{k} < G_{k, 1} + h \\ 2, G_{k, 1} + h \leq {t^{l}}_{k} < G_{k, 1} + G_{k, 2} + 2 h \\ 3, G_{k, 1} + G_{k, 2} + 2 h \leq {t^{l}}_{k} < \\ G_{k, 1} + G_{k, 2} + G_{k, 3} + 3 h \\ ⋮ ⋮ \\ N, \overset{N - 1}{\sum_{i = 1}} G_{k, i} + (N - 1) h \leq {t^{l}}_{k} < C_{k} \end{matrix} \end{matrix}$ (2)

式中:G_k_,_i为节点k第i相位的绿灯时长。

为便于等待时间的计算, 在式(2)中, 若机动车于相位间隔时间内到达, 将其划入前一个相位。

1.2 信号交叉口等待时间计算

信号交叉口等待时间取决于机动车的到达相位和离开相位, 文献[14]指出相位切换将导致等待时间发生突变, 但其忽略了相位间隔时间h。相位间隔时间由黄灯时间和全红时间组成, 此间到达停车线的机动车必须停车等待, 因此等待时间的变化也会受到影响。本文在对信号交叉口等待时间进行计算时, 将考虑相位间隔时间h。

设机动车的离开相位为m, 显然, 当离开相位m与到达相位n相等时, 等待时间为0。

(1)离开相位m大于到达相位n

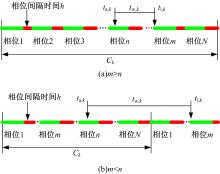
如图3(a)所示, 该情况下, 机动车可于本周期内离开交叉口。节点k的信号交叉口等待时间为:

$\begin{matrix} \begin{matrix} t_{w, k} = \overset{n}{\sum_{i = 1}} G_{k, i} + n h - {t^{l}}_{i} + \overset{m - 1}{\sum_{i = n + 1}} G_{k, i} + (m - \\ 1 - n) h = \overset{n}{\sum_{i = 1}} G_{k, i} + n h - (t_{a, k} - \\ θ_{k}) \mod C_{k} + \overset{m - 1}{\sum_{i = n + 1}} G_{k, i} + (m - 1 - n) h = \\ \overset{m - 1}{\sum_{i = 1}} G_{k, i} + (m - 1) h - (t_{a, k} - θ_{k}) \mod C_{k} \end{matrix} \end{matrix}$ (3)

	Figure Option View Download New Window
	图3 等待时间计算示意图Fig.3 Schematic diagram of waiting time computing

(2)离开相位m小于到达相位n

如图3(b)所示, 该情况下, 机动车需于下一个周期离开交叉口。节点k的信号交叉等待时间为:

$\begin{matrix} \begin{matrix} t_{w, k} = \overset{n}{\sum_{i = 1}} G_{k, i} + n h - {t^{l}}_{k} + \overset{N}{\sum_{i = n + 1}} G_{k, i} + \\ (N - n) h + \overset{m - 1}{\sum_{i = 1}} G_{k, i} + (m - 1) h = \\ (\overset{n}{\sum_{i = 1}} G_{k, i} + \overset{N}{\sum_{i = n + 1}} G_{k, i} + N h) + \\ \overset{m - 1}{\sum_{i = 1}} G_{k, i} + (m - 1) h - {t^{l}}_{k} = \\ (\overset{n}{\sum_{i = 1}} G_{k, i} + \overset{N}{\sum_{i = n + 1}} G_{k, i} + N h) + \\ \overset{m - 1}{\sum_{i = 1}} G_{k, i} + (m - 1) h - (t_{a, k} - θ_{k}) \mod C_{k} = \\ C_{k} + \overset{m - 1}{\sum_{i = 1}} G_{k, i} + (m - 1) h - (t_{a, k} - θ_{k}) \mod C_{k} \end{matrix} \end{matrix}$ (4)

(3)右转绕行

绝大多数情况下, 右转车辆不受信号灯控制, 即到即走, 通常假设其等待时间为0。但由于右转车辆需给行人或非机动车让行, 会产生微小的随机等待时间, 因此, 为右转车辆加上一定的惩罚时间, 对模型进行修正。

$\begin{matrix} t_{w, k} = d_{r, k} \end{matrix}$ (5)

式中:d_r,_k为节点k的右转平均停车时间, d_r,_k可由实际交通调查采集获得。

少部分交叉口对右转车流有专门的信号控制, 对于此类右转车辆, 根据其到达和离开相位计算等待时间, 分析方法与前文相似, 在此不做赘述。为简化模型, 本文假设对交叉口右转车辆均采用无信号控制。

2 改进的IDA^*算法

A^*算法是目前广泛采用的启发式搜索算法, 搜索效率优于传统dijkstra算法, 但A^*算法的内存占用较高, 且需要占用较多时间进行判重检测, 影响了搜索效率。IDA^*算法将A^*算法与迭代加深算法结合, 其基本思想为:

(1)设置一个初始最大估价值maxf。

(2)开始深度优先搜索, 若节点估价值f大于maxf, 则对其进行剪枝。

(3)若搜索完成没有找到目标节点, 则增加maxf, 返回步骤(2), 直至找到目标节点。

IDA^*算法减小了资源消耗, 且无需判重检测, 能够提高搜索效率^[15], 因此, 本文将信号交叉口等待时间模型叠加进IDA^*算法, 提出了考虑干线协调配时的改进IDA^*算法(AICIDA^*算法)。

2.1 路网表达存储模型

为了将本文等待时间模型叠加进IDA^*算法, 首先要对路网中相邻路段的通行方向和对应的信号相位进行表达和存储。传统的邻接矩阵、邻接表和星型表结构难以满足要求。本文结合对偶图思想, 提出了一种改进的星型表结构, 以表达AICIDA^*算法所需信息。

以图4所示路网为例, 其改进星型表结构如图5所示。

	Figure Option View Download New Window
	图4 示例路网Fig.4 Sample network

	Figure Option View Download New Window
	图5 改进的星型表结构Fig.5 Improved forward star structure

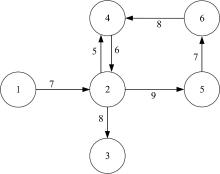
图5中, ArcID数组存储路段信息; Linkcost数组存储路段权重, 即路段行程时间; Pointer数组为指针数组, 初始指向每一条路段的第一条后继路段, 若路段没有后继路段(如路段2-3和2-4), 则指针悬空, 赋值NULL; PointedarcID数组存储后继路段信息, 若有多条后继路段, 则按ArcID中的顺序进行排列; Movetype数组存储从路段i到其后继路段j的通行方向mt_k_,_i_,_j, 若为左转或直行, 则mt_k_,_i_,_j=1, 若为右转, 则mt_k_,_i_,_j=2, 如此划分是因为右转的控制方式与直行/左转不同, 等待时间的计算方式也不同; Relaynode数组储存路段i的末端节点k, 节点k也是路段i与其后继路段j的中继节点; Phaseorder数组存储从路段i到路段j通行方向在中继节点k处所属的信号相位, 若为右转通行, 则不属于任何相位, 赋值为NULL。

以路段1-2为例, 其末端节点为节点2, 三条后继路段依次为2-3, 2-4, 2-5, Relaynode皆赋值为2, 路段1-2至路段2-3为右转, 故mt_{2, 1}_-_{2, 2}_-₃=2, Phaseorder赋值NULL; 路段1-2至路段2-4为左转, 为节点2第3相位, 故mt_{2, 1}_-_{2, 2}_-₄=1, Phaseorder赋值3; 路段1-2至路段2-5为直行, 为节点2第1相位, 故mt_{2, 1}_-_{2, 2}_-₅=1, Phaseorder赋值1。由此, 通过改进的星型表即可完整表达邻接路段的通行方向, 以及其对应的信号交叉口相位。

对于节点信息的存储, 除了存储其名称、坐标等信息, 还应存储如下信息:①判别信息A_k, 若节点k为信号交叉口, A_k=1, 否则A_k=0; ②信号交叉口配时信息, 包括信号周期C_k、绝对相位差值θ _k、相位间隔时间h、各相位绿灯时间G_k_,_i、右转平均停车时间d_r,_k, 若节点k并非信号交叉口, 配时信息皆赋值为NULL, 且在星型表中Phaseorder赋值为NULL。

2.2 AICIDA^*算法流程

IDA^*算法的估价函数与A^*算法相似, 不同之处在于算法流程。AICIDA^*算法以路段为搜索对象, 但路径费用的计算依赖路段的末端节点, 为了表述简便, 规定AICIDA^*算法以“ 弧节点” 为搜索对象, “ 弧节点” 定义如下:弧节点i即为沿路段i驶达的末端节点k(i)。每一个弧节点代表一条路段, 同时指向它的末端节点, 与路网表达模型相对应。

AICIDA^*算法的估价函数为:

$\begin{matrix} \{\begin{matrix} f (j) = g (j) + h (j) \\ F_{maxo} = D (o) / V_{mlim} \\ s . t . g (j) = t_{a, k} (j) - t_{a, k} (o) \\ t_{a, k} (j) = t_{l, k} (i) + ω_{j} \\ t_{l, k} (i) = t_{a, k} (i) + t_{w, k} (i) \\ h (j) = D (j) / V_{mlim} \end{matrix} \end{matrix}$ (6)

式中:f(j)为弧节点j估价值; g(j)为弧节点j实际费用, 即从起始弧节点o行驶至弧节点j所消耗的时间; h(j)为弧节点j到目标弧节点的估计费用(耗时); F_max_o为初始最大估价值; D(o)为起始弧节点与目标弧节点的欧氏距离; V_mlim为路网最高限速值; t_a,_k(j)为弧节点j的到达时刻; t_a,_k(o)为起始弧节点o的到达时刻; t_a,_k(i)、t_l,_k(i)分别为上游弧节点i的到达、离开时刻; ω _j为路段j权重, 即路段j的行程时间; t_w,_k(i)为弧节点i的信号交叉口等待时间; D(j)为弧节点j与目标弧节点的欧氏距离。

AICIDA^*算法必定寻到最优解的条件为h(j)小于等于实际费用, 由于本文h(j)为两点直线距离与最高限速值之比, 因此h(j)必然小于等于两点间的实际费用, 故CWTIDA^*算法必定能找到最优解。

AICIDA* 算法流程如下所示。

Step1 初始化, 设所有弧节点f、g为∞ , maxf=F_max_o。

Step2 令初始弧节点作为当前父节点i, 更新g(i)=0, 按存储顺序以其第一个后继弧节点为当前子节点j。

Step3 按以下步骤计算当前子节点j的估价值f(j):

Step3.1 按式(7)计算当前父节点i的到达时刻t_a,_k(i):

$\begin{matrix} t_{a, k} (i) = g (i) + t_{a, k} (o) \end{matrix}$ (7)

Step3.2 对A_k进行判别:若A_k=0, 则末端节点k(i)不是信号交叉口, t_w,_k(i)=0, 转Step3.6; 若A_k=1, 转Step3.3。

Step3.3 对mt_k_,_i_,_j进行判别:若mt_k_,_i_,_j=1, 转Step3.4; 若mt_k_,_i_,_j=2, 按式(5)计算t_w,_k(i), 转Step3.6。

Step3.4 按式(1)(2)计算到达相位n。

Step3.5 对mt_k_,_i_,_j对应相位m进行判别:若m> n, 按式(3)计算t_w,_k(i); 若m< n, 按式(4)计算t_w,_k(i); 若m=n, t_w,_k(i)=0, 转Step3.6。

Step3.6 按式(8)计算当前子节点j的当前实际费用g(j):

$\begin{matrix} g (j) = g (i) + t_{w, k} (i) + ω_{j} \end{matrix}$ (8)

若当前g(j)小于原先值, 则更新g(j), 并按式(6)计算f(j); 否则g(j)、f(j)保留原值。

Step4 对f(j)进行判别:若f(j)≤ maxf, 则将当前子节点j标为当前父节点i, 按存储顺序以其第一个后继弧节点为当前子节点j, 转Step3; 若f(j)> maxf, 进行剪枝, 存储该溢出值OF(j)=f(j), 转Step5。

Step5 若当前父节点i有其他未访问后继弧节点, 则以其下一个后继弧节点为当前子节点j, 转Step3; 若当前父节点i已无未访问后继弧节点, 转Step6。

Step6 回溯, 将当前父节点i的父节点标为当前父节点i, 转Step5; 直至起始弧节点o无未访问后继弧节点, 转Step7。

Step7 终止条件判别:若在当前maxf下目标弧节点d被访问完毕, 则找到最优路径, 转Step8; 若当前maxf下未寻到目标弧节点d, 将最小溢出值赋给maxf, maxf=min{OF(j)}, 转Step2; 若访问路网所有可达弧节点仍未找到目标弧节点d, 则d不可达, 算法终止。

Step8 输出最优路径, 以及路径上所有末端节点, 算法结束。

从上述流程可看出:CWTIDA^*算法无需判重操作, 也无需每拓展一次弧节点就进行排序操作, 只需对溢出的估价值OF(j)进行排序, 因此节省了相关操作时间, 并大幅缩减了内存占用, 节省了部分内存回收再分配所需时间, 适用于可拓展节点多、节点包含信息量多的大范围路网。

3 算例验证

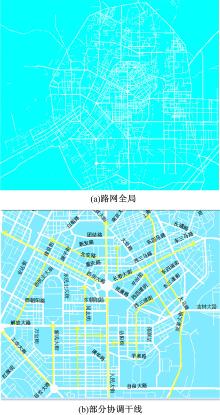
以长春市某路网为算例路网, 如图6(a)所示, 算例路网共包含节点3421个, 路段5771条。采用Mapinfo7.0+MapX插件为地图平台, 采用Visual C++ 6.0对本文算法进行编程实现, 采用2.1节的改进星型表结构对路网信息进行存储。算例条件设置如下:

(1)将节点中的交叉口均设置为信号交叉口, 赋予配时参数。对于环形交叉口, 以其作为中继节点的所有通行方向均视为右转, Phaseorder赋值为NULL, 按照式(5)计算等待时间。

(2)在路网中选取部分路径作为协调控制路径, 路径上的信号交叉口采用协调控制, 如图6(b)所示。协调方向如箭头线所示, 每一个交叉口至多参与一条干线协调, 即箭头线并无相交。

	Figure Option View Download New Window
	图6 算例路网示意图Fig.6 Schematic diagram of the example road network

(3)基准时刻设为0, 起始弧节点到达时刻t_a,_k(o)设为200 s, 路网最高限速V_mlim设为70 km/h, 对于参与协调的交叉口, 协调方向设为第一相位。其中一条干线的部分交叉口配时参数如表1所示(协调设计车速设置为40 km/h)。

选择一对OD点对, 用以下4种算法搜索最优路径:经典dijkstra算法、文献[14]提出的CWTSI-SP算法、叠加本文等待时间模型的A^*算法(AICA^*算法)、本文所提AICIDA^*算法。搜索结果如图7所示, 其中五角星代表起讫点, 黑色箭头代表沿此路段进入起点。分别计算各路径的路径总费用(路径总费用=路段权重之和+路径上所有交叉口的等待时间之和), 如表2所示。

表1 部分协调交叉口配时参数 Table 1 Signal-timing of partial coordinate intersections s

	Figure Option View Download New Window
	图7 不同搜索算法所求最优路径Fig.7 Shortest paths from different searching algorithm

表2 不同搜索算法所求路径总费用 Table 2 Total path cost of different searching algorithms

由图(7)和表2可知:

(1)CWTSI-SP算法所得的路径总费用高于AICA^*算法和AICIDA^*算法, 这是由于CWTSI-SP算法虽然考虑了信号交叉口等待时间, 却没有考虑干线协调情况, 其默认一条干线的通行方向绿灯均在同一时间启亮, 因此当路网存在干线协调时, 其计算出的等待时间将出现偏差, 不仅如此, CWTSI-SP算法没有考虑相位间隔时间, 将使偏差进一步加大, 因此影响了实际效果。

(2)AICA^*算法和AICIDA^*算法计算出的最优路径相同, 且路径总费用低于前两种算法, 这是由于这两种算法都叠加了本文的等待时间模型, 且都能求得最优解, 故解相同。而本文的等待时间模型考虑了干线协调控制与相位间隔时间, 故计算出的等待时间更加准确, 所得最优路径更加贴合实际。比照图7和图6(b)可以看出, AICA^*算法和AICIDA^*算法所得路径更好地利用了具有协调控制的路段, 有效降低了路径总费用。

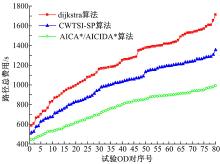
为进一步验证4种算法的效果, 选择80组OD对进行试验, 按照路径总费用大小对试验结果进行排序, 如图8所示。从图8可以看出:随着路径总费用的上升, 意味着OD对相隔越来越远, 需要经过的信号交叉口就会越来越多, 传统算法不能准确地考虑交叉口等待时间, 且信号相位切换可能使等待时间突增, 故传统算法的曲线增幅较大, 且不够平滑, 本文算法较为准确地考虑了交叉口等待时间, 能够更准确地选择总费用更低的路径, 且回避等待时间过高的通行方向, 故曲线增幅相对较小, 且更加平滑。

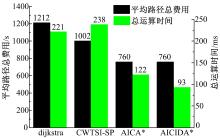
	Figure Option View Download New Window
	图8 四种算法路径总费用对比Fig.8 Total path cost comparison of four algorithms

80组试验OD对的平均路径总费用和总运算时间如图9所示。从图9可以看出:在平均路径总费用方面, AICIDA^*算法比dijkstra算法下降了37.3%, 比CWTSI-SP算法下降了24.2%, 与AICA^*算法相同; 在总运算时间方面, AICIDA^*算法比dijkstra算法下降了57.9%, 比CWTSI-SP算法下降了60.9%, 由于CWTSI-SP算法在dijkstra算法的基础上叠加了等待时间, 故运算时间稍高于dijkstra算法。与AICA^*算法相比, AICIDA^*算法运算时间下降了23.8%, 这是由于AICIDA^*算法不需判重操作, 且排序操作相对较少, 同时大幅减小了内存消耗, 节省了部分内存回收再分配的时间。综上所述, AICIDA^*算法在综合性能上优于传统算法。

	Figure Option View Download New Window
	图9 四种算法综合性能对比Fig.9 Overall performance of four algorithms

4 结束语

提出了一种考虑干线协调控制的最短路径搜索算法。通过对干线协调控制情况进行分析, 引入相位差参数对信号交叉口等待时间进行建模。在此基础上, 将信号交叉口等待时间模型叠加进IDA^*算法, 提出了考虑干线协调控制的AICIDA^*算法。算例验证结果表明:AICIDA^*算法的效果优于传统dijkstra算法、考虑信号交叉口等待时间的CWTSI-SP算法和叠加本文等待时间模型的AICA^*算法, 搜索得到的路径总费用更低, 且搜索速度更快。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	徐长斌, 刘艳梅. 动态路径诱导算法研究[J]. 公路交通科技: 应用技术版, 2007, 3(10): 35-36. Xu Chang-bin, Liu Yan-mei. The research of algorithm on dynamic path guidance[J]. Journal of Highway and Transportation Research and Development(Applied Technique), 2007, 3(10): 35-36. [本文引用:1]
[2]	Bolívar M A, Lozano L, Medaglia A L. Acceleration strategies for the weight constrained shortest path problem with replenishment[J]. Optimization Letters, 2014, 8(8): 2155-2172. [本文引用:1]
[3]	Klunder G A, Post H N. The shortest path problem on large-scale real-road networks[J]. Networks, 2006, 48(4): 182-194. [本文引用:1]
[4]	Kim J, Han W S. Processing time-dependent shortest path queries without pre-computed speed information on road networks[J]. Information Sciences, 2014, 255(1): 135-154. [本文引用:1]
[5]	盖文妹, 邓云峰, 蒋仲安, 等. 双权重应急交通网络最优路径数学模型及算法研究[J]. 中南大学学报: 自然科学版, 2014(6): 2366-2375. Gai Wen-mei, Deng Yun-feng, Jiang Zhong-an, et al. Model and its fast approximation algorithm of optimal route in a dual-weight emergency transportation network[J]. Journal of Central South University(Science and Technology), 2014(6): 2366-2375. [本文引用:1]
[6]	杨庆芳, 梅朵. 基于云计算的城市路网最短路径遗传算法求解[J]. 华南理工大学学报: 自然科学版, 2014, 42(3): 47-58. Yang Qing-fang, Mei Duo. Cloud computing-based genetic algorithm to solve the shortest path in urban road networks[J]. Journal of South China University of Technology(Natural Science Edition), 2014, 42(3): 47-58. [本文引用:1]
[7]	Hoang V D, Jo K H. Path planning for autonomous vehicle based on heuristic searching using online images[J]. Vietnam Journal of Computer Science, 2015, 2(2): 109-120. [本文引用:1]
[8]	杜长海, 黄希樾. 改进的蚁群算法在动态路径诱导中的应用研究[J]. 计算机工程与应用, 2008, 44(27): 236-239. Du Chang-hai, Huang Xi-yue. Study on application of improved ant colony algorithm in dynamic route guidance[J]. Computer Engineering and Applications, 2008, 44(27): 236-239. [本文引用:1]
[9]	Frangioni A, Galli L, Scutellà M G. Delay-constrained shortest paths: approximation algorithms and second-order cone models[J]. Journal of Optimization Theory and Applications, 2015, 164(3): 1051-1077. [本文引用:1]
[10]	高淑萍, 赵会宾. 基于信号配时的动态路径诱导模型[J]. 中国公路学报, 2011, 24(1): 109-114. Gao Shu-ping, Zhao Hui-bin. Dynamic route guidance model based on signal lamp time assignment[J]. China Journal of Highway and Transport, 2011, 24(1): 109-114. [本文引用:1]
[11]	杨琰, 廖伟志, 李文敬. 基于Petri网的顾及转向延误的最优路径算法[J]. 计算机工程与设计, 2013(10): 3643-3648. Yang Yan, Liao Wei-zhi, Li Wen-jing. Intelligent routing algorithm considering turn delays based on Petri net[J]. Computer Engineering and Design, 2013(10): 3643-3648. [本文引用:1]
[12]	黄美灵, 陆百川. 考虑交叉口延误的城市道路最短路径[J]. 重庆交通大学学报: 自然科学版, 2009, 28(6): 1060-1063. Huang Mei-ling, Lu Bai-chuan. Determination of the shortest path considering delays at intersections[J]. Journal of Chongqing Jiaotong University(Natural Science Edition), 2009, 28(6): 1060-1063. [本文引用:1]
[13]	李继伟. 城市主次干路的路段行程时间估计与预测方法研究[D]. 长春: 吉林大学交通学院, 2012. Li Ji-wei. Estimation and prediction of link travel time for urban trunk and secondary streets[D]. Changchun: College of Transportation, Jilin University, 2012. [本文引用:1]
[14]	杨帆, 杨晓光. 考虑信号交叉口等待时间的最短路径算法[J]. 同济大学学报: 自然科学版, 2013, 41(5): 680-686. Yang Fan, Yang Xiao-guang. Shortest path algorithm with a consideration of waiting time at signalized intersections[J]. Journal of Tongji University(Natural Science Edition), 2013, 41(5): 680-686. [本文引用:1]
[15]	Mencía C, Sierra M R, Varela R. *Intensified iterative deepening A with application to job shop scheduling*[J]. Journal of Intelligent Manufacturing*, 2014, 25(6): 1245-1255. [本文引用:1]

2007

0.0

... 现有路径搜索算法主要包括标号法^[1,2,3]和启发式算法^[4,5,6,7,8],多数算法仅考虑路段行程时间,忽略了车辆在交叉口处的等待时间,导致所得最优路径实际效果不佳 ...

2014

0.0

2006

0.0

2014

0.0

2014

0.0

. 2014, 42(3):47-58 DOI:doi:10.3969/j.issn.1000-565X.2014.03.008

Cloud computing-based genetic algorithm to solve the shortest path in urban road networks

基于云计算的城市路网最短路径遗传算法求解

Yang Qing-fang , Mei Duo.

杨庆芳, 梅朵

针对城市路网最短路径求解过程中计算量庞大的问题，在分析遗传算法特征和缺陷的基础上，提出了基于MapReduce的并行遗传算法，并以长春市路网特征数据为基础验证了该算法的有效性。实验结果表明：基于 MapReduce的并行遗传算法较传统遗传算法收敛速度快，运行时间短；随着并行节点数的增加，节点间的通信负荷加重，因此恰当地选择节点数尤为重要，合适的节点数可以提高运行效率。

2015

0.0

2008

0.0

. 2008, 44(27):236-239 DOI:doi:10.3778/j.issn.1002-8331.2008.27.075

Study on application of improved ant colony algorithm in dynamic route guidance

改进的蚁群算法在动态路径诱导中的应用研究

Du Chang-hai , Huang Xi-yue.

杜长海, 黄希樾

Due to the disadvantage of relatively slow convergence and local optimum of basic ant colony algorithm，based on eliminating the influence of the size and dimension of pheromone and heuristic information through standardized transformation，directed pheromone updating on and chaotic selection strategy are proposed to improve ant colony algorithm.Relative location information among nodes in road network is introduced in pheromone updating for higher searching speed，and chaos perturbation is used to improve selection strategy to avoid precocity and stagnation.Then the improved ant colony algorithm is applied in urban traffic dynamic route guidance.The road network of Chongqing Yuzhong Peninsula is taken as an example to calculate the optimal route based on the least travel time，and the experimental results show that this algorithm has much higher capacity of global optimization than basic ant colony algorithm and it is feasible and effective for optimal route choice.

针对基本蚁群算法收敛速度慢和易陷入局部最优的缺点，在对信息素和启发信息进行标准化以消除量纲和取值范围影响的基础上，提出带方向的信息素更新和混沌选择策略来改进蚁群算法。将路网节点间的相对位置信息引入信息素更新，以加快搜索速度；使用混沌扰动改进选择策略，以避免出现早熟停滞现象。并将其用于城市交通动态路径诱导的研究中，以重庆市渝中半岛的路网为实例计算以最短行程时间为目标的最优路径，结果表明该算法是有效、可行的，比基本蚁群算法具有更好的全局搜索能力。

2015

0.0

... 此类方法将延误模型叠加进路径搜索算法^[9,10,11,12],或在路段划分时将交叉口作为路段的一部分,将平均信号延误计入路段权重^[13] ...

2011

0.0

. 2011, 24(1):109-114 DOI:doi:10.1080/0144929X.2011.553739

Dynamic route guidance model based on signal lamp time assignment

基于信号配时的动态路径诱导模型

Gao Shu-ping , Zhao Hui-bin.

高淑萍, 赵会宾

Aimed at the problem due to changes of the urban traffic flow, based on the improvement of the project of intersections signal lamp, bi-level optimal model of dynamic route guidance was established. In the upper level model, the minimization of travel time was used as the objective function; in the lower level model, the minimization of intersection delay was used as the objective function. Improved ant colony system algorithm (IACA) was applied to solution and improvement of the model, and multi-strip quasi-optimal routes were obtained. Taking practical intersections as example, calculated results of model before and after improvement of signal lamp time assignment were compared. Results show that the model after improvement of signal lamp time assignment can find more time-saving route and less waiting time of intersections.

针对城市交通流量变化产生的问题,在交叉口信号灯配时方案改进的基础上建立了动态路径诱导的双层优化模型,上层模型以行驶时间为目标函数,下层模型以总交叉口延误最小为目标函数。利用改进蚁群算法来求解优化模型,从而获得多准最优路径。以实际交叉口为例,将信号灯配时改进前、后的模型计算结果进行比较。结果表明:应用信号灯配时改进后的模型获得的路径更省时,交叉口等待通行时间更短。

... 此类方法将延误模型叠加进路径搜索算法^[9,10,11,12],或在路段划分时将交叉口作为路段的一部分,将平均信号延误计入路段权重^[13] ...

0.0

... 此类方法将延误模型叠加进路径搜索算法^[9,10,11,12],或在路段划分时将交叉口作为路段的一部分,将平均信号延误计入路段权重^[13] ...

2009

0.0

. 2009, 28(6):1060-1063 DOI:doi:10.3969/j.issn.1674-0696.2009.06.22

Determination of the shortest path considering delays at intersections

考虑交叉口延误的城市道路最短路径

Huang Mei-ling , Lu Bai-chuan.

黄美灵, 陆百川

在利用GIS建立城市道路网并通过空间分析判断节点方位和路径走向的基础上,提出了一种具有节点阻抗的Floyd算法来解决城市道路网中的最短路径问题,这里直行、左转或右转的分流向延误得到了充分考虑.最后利用所提出的算法对重庆市石桥铺街道路网进行了分析计算,得出了比传统方法更合理的结果.

... 此类方法将延误模型叠加进路径搜索算法^[9,10,11,12],或在路段划分时将交叉口作为路段的一部分,将平均信号延误计入路段权重^[13] ...

2012

0.0

. 2012, :-

Estimation and prediction of link travel time for urban trunk and secondary streets[D]. Changchun: College of Transportation,

城市主次干路的路段行程时间估计与预测方法研究[D]

Li Ji-wei.

李继伟

... 此类方法将延误模型叠加进路径搜索算法^[9,10,11,12],或在路段划分时将交叉口作为路段的一部分,将平均信号延误计入路段权重^[13] ...

2013

0.0

. 2013, 41(5):680-686 DOI:doi:10.3969/j.issn.0253-374x.2013.05.008

Shortest path algorithm with a consideration of waiting time at signalized intersections

考虑信号交叉口等待时间的最短路径算法

Yang Fan , Yang Xiao-guang.

杨帆, 杨晓光

在甄别等待时间和延误的基础上,首先提出了信号交叉口处等待时间函数,并分析了信号交叉口处等待时间特性；其次,在假设路段行程时间固定的基础上重新定义路网的邻接矩阵,提出信号交叉口属性表,并结合重新定义的路网参数,将信号交叉口等待时间引入算法之中,提出了新的标号算法,即考虑信号交叉口等待时间的最短路径算法(CWTSI-SP algorithm),用以求解本文网络最短路径问题.数值试验的结果表明,CWTSI-SP算法考虑了信号交叉口的等待时间,并分析了最短路径和最短行程时间随开始时间的不同而变化的特性.算法具有较好的效率,并贴近交通现象本质,对于动态交通流分析具有良好的实用性.

... ②根据车辆到达交叉口的时刻对单个车辆的信号交叉口等待时间进行建模,此类方法考虑了当前相位状态,计算车辆在不同相位离开时所需的等待时间,与第一类方法相比更加贴合实际^[14] ...

2014

0.0

... 算法减小了资源消耗,且无需判重检测,能够提高搜索效率^[15],因此,本文将信号交叉口等待时间模型叠加进IDA^{#cod#x0002A ...}