基于L-M算法的正交Stewart平台位姿正解的初值补偿

引用本文

王启明, 苏建, 张兰, 陈秋雨, 徐观. 基于L-M算法的正交Stewart平台位姿正解的初值补偿. 2017, 47(1): 97-104
WANG Qi-ming, SU Jian, ZHANG Lan, CHEN Qiu-yu, XU Guan. Forward kinematics of orthogonal Stewart platform based on L-M algorithm. Journal of Jilin University Engineering and Technology Edition, 2017, 47(1): 97-104 复制到剪切板

Permissions

基于L-M算法的正交Stewart平台位姿正解的初值补偿

王启明, 苏建, 张兰, 陈秋雨, 徐观

吉林大学交通学院,长春 130022

通讯作者:苏建(1954-),男,教授,博士生导师.研究方向:车辆智能检测.E-mail:sujianjd@163.com

作者简介:王启明(1991-),女,博士研究生.研究方向:车辆智能检测.E-mail:wang.qiming2008@163.com

基金:国家自然科学基金项目(51478204).

摘要

针对牛顿拉夫逊迭代法求解正交Stewart六自由度平台位姿正解对迭代初值依赖的问题,提出基于Levenberg-Marquardt(L-M)算法改进的BP神经网络模型,进而实现对Stewart平台位姿正解的迭代初值补偿值计算,并与基于BFGS拟牛顿算法、SCG量化共轭梯度算法、GDA梯度下降自适应算法所建立的BP神经网络模型进行对比分析,重点分析模型的适应性、预测输出、误差性能等。结果表明:采用提出的基于L-M算法改进的BP神经网络模型对正交Stewart六自由度平台位姿正解的迭代初值校正后,收敛速度有显著提升,初始值校正误差低于0.1%,校正结果满足预期要求。

关键词: 铁路运输; 位姿正解; 轨道车辆; 位姿测量系统; Levenberg-Marquardt算法; 牛顿拉夫逊迭代法

中图分类号:U266 文献标志码:A 文章编号:1671-5497(2017)01-0097-08

Forward kinematics of orthogonal Stewart platform based on L-M algorithm

WANG Qi-ming, SU Jian, ZHANG Lan, CHEN Qiu-yu, XU Guan

College of Transportation, Jilin University, Changchun 130022, China

Abstract

Aiming at the problem of high sensitivity to iteration initial guess when using Newton-Raphson iteration method to compute the forward kinematic solution of orthogonal Stewart-6D- platform, a compensation method based on Levenberg-Marquardt (L-M) algorithm of back propagation model iteration initial guess was proposed. The adaptation, the output prediction and error performance of the proposed algorithm were analyzed in comparison with the back propagation model based BFGS quasi-Newton algorithm, back propagation model based scale conjugate gradient, back propagation model based gradient descent with adaptive Ir algorithm. With the help of inverse solution model based Simulink and SolidWorks, successful training samples were established. 1000 groups of data were randomly and comprehensively picked up. 900 groups were used for training the net and the other 100 groups were used for testing whether the trained net is qualified. Simulation results show that the initial guess modified L-M algorithm of back propagation model was significantly calibrated. The convergent speed of the iteration modified algorithm was improved. The angle and displacement calibrating error rate was less than 0.1%. The test results of the improved BP Neural net can meet the requirement.

Keyword: railway transportation; forward kinematics; railway vehicles; pose measurement system; Levenberg-Marquardt(L-M) algorithm; Newton-Raphson iteration

Show Figures

0 引言

中国高速铁路的跨越式发展对高速轨道列车设计技术提出了更高的要求。车辆端部和转向架是轨道车辆的重要组成部分, 列车在运行过程中, 经过曲线轨道、道岔及变坡点或者受到牵引力、制动力作用时, 相邻的两车车体间会产生不同程度的相对运动。如果相对运动过大, 极容易导致车端和连接装置之间发生干涉, 轻则会损耗车端及车端连接装置, 重则会诱发安全事故。因此有必要对车端部件在不同路况下的运动位姿进行检测。针对以上问题, 本文开发了车端运动位姿检测系统, 可抽象为正交Stewart六自由度运动平台, 将平台的两端分别安装在相邻两节车厢端部车钩位置, 实现车端运动位姿的测量。正交Stewart六自由度运动平台属于并联型六自由度运动机构, 具有运动空间小、鲁棒性强、惯性小、运动精度高以及成本较低等优点。然而, 由于正交Stewart六自由度运动平台具有高耦合性、非线性等特点, 其位姿正解的求解一直是个难题。位姿正解^[1]的求解对于六自由度工作空间分析、机构设计以及机构在故障中恢复均有重要作用, 因此, 合理有效快速的位姿正解求解方法是十分必要的。目前, 位姿正解求解方法主要包括解析法^{[2, 3, 4]}和数值法^[5]两种。解析法是通过构建多组约束方程并利用多种方法消去未知数的方法。该方法缺点在于求解过程复杂、消元方法不确定, 且解的个数众多不易得出实用解, 无法满足实时控制需求, 通用性较差。数值法采用迭代法求解, 对迭代初值的要求较高, 初值选取不当则会致使迭代无法收敛^[6], 进而导致无法获取正确解。

因此, 针对上述问题, 提出基于L-M算法的BP神经网络算法模型, 对位姿正解的迭代初值进行补偿和校正。该补偿算法主要以BP神经网络为基础, 结合正交Stewart六自由度运动平台的结构特性, 融合L-M算法对六自由度位姿正解的输入进行非线性校正, 进而有效地解决位姿正解的迭代初始值补偿问题。

1 正交Stewart六自由度运动平台

车端位姿测量装置主要由两个六边形平台构成, 分别为上平台和下平台。在实际测量过程中, 上、下平台分别安装在相邻两车厢端部车钩位置处。如图1所示, 下平台处分布有6个位移传感器 $\begin{matrix} A_{1} ~ A_{6}, \end{matrix}$ 上平台连接6个拉线式位移传感器的末端 $\begin{matrix} B_{1} ~ B_{6}, \end{matrix}$ 进而确保上、下平台正交。本文借助SolidWorks建模分析, 将车端位姿测量装置抽象为结构尺寸一致的上、下两平台, 在两个平台上各分布6个球铰, 且上、下平台通过6个杆铰接, 形成正交六自由度平台结构。

	Figure Option View Download New Window
	图1 正交Stewart六自由度运动平台Fig.1 Orthogonal Stewart-6 dof-platform

图1中, 上部动平台A与下部静平台B尺寸和结构相同, 在运动初始位置时两平台同轴, 且上平台各端面均对应平行于下平台各端面。下部静平台B₁点(传感器B₁点)与上部动平台的A₁点(传感器A₁点)通过伸缩杆L₁连接, 同时, 下部静平台的B₂点与上部动平台的A₂点通过杆L₂连接, 顺时针依次类推。

借助SolidWorks软件和Simulink仿真平台建立六自由度平台位姿反解模型, 将位姿反解模型中的位姿量及对应的杆长伸缩量, 作为改进BP神经网络模型^[7]训练样本。通过采用大量样本的训练学习, 使得改进的BP神经网络能够预测位姿值, 将此值作为位姿正解的迭代初值, 进而能够有效缩短迭代运算时间, 提高位姿正解精度。

2 位姿正解数学模型

2.1 位姿正解数学模型的建立

结合六自由度运动平台的几何结构, 如1图所示, 选取下部静平台B中心作为静坐标系原点O₁, 体坐标系原点 $\begin{matrix} O_{2} \end{matrix}$ 与静坐标系原点 $\begin{matrix} O_{1} \end{matrix}$ 重合, 规定如图1所示的坐标轴分别为 $\begin{matrix} X \end{matrix}$ 轴、 $\begin{matrix} Y \end{matrix}$ 轴、 $\begin{matrix} Z \end{matrix}$ 轴。根据六自由度平台的结构尺寸可得 $\begin{matrix} A_{i} 、 B_{i} 点 (i = 1, 2, \dots, 6) \end{matrix}$ 在体坐标系和静坐标系的表达式分别为:

$A = [\begin{matrix} \begin{matrix} 298.5 \\ - 30 \\ 335 \\ 1 \end{matrix} & \begin{matrix} - 123.27 \\ - 273.51 \\ 335 \\ 1 \end{matrix} & \begin{matrix} - 175.23 \\ - 243.51 \\ 335 \\ 1 \end{matrix} & \begin{matrix} \begin{matrix} - 175.23 \\ 243.51 \\ 335 \\ 1 \end{matrix} & \begin{matrix} - 123.27 \\ 273.51 \\ 335 \\ 1 \end{matrix} & \begin{matrix} 298.5 \\ 30 \\ 335 \\ 1 \end{matrix} \end{matrix} \end{matrix}]$ (1)

$B = [\begin{matrix} \begin{matrix} 175.23 \\ - 243.51 \\ 0 \\ 1 \end{matrix} & \begin{matrix} 123.27 \\ - 273.51 \\ 0 \\ 1 \end{matrix} & \begin{matrix} - 298.5 \\ - 30 \\ 0 \\ 1 \end{matrix} & \begin{matrix} \begin{matrix} - 298.5 \\ 30 \\ 0 \\ 1 \end{matrix} & \begin{matrix} 123.27 \\ 273.51 \\ 0 \\ 1 \end{matrix} & \begin{matrix} 175.23 \\ 243.51 \\ 0 \\ 1 \end{matrix} \end{matrix} \end{matrix}]$ (2)

体坐标系相对于静坐标系可用广义坐标 $\begin{matrix} q_{i} (i = 1, 2, \dots, 6) \end{matrix}$ 来描述, $\begin{matrix} q_{1} 、 q_{2} 、 q_{3} \end{matrix}$ 为体坐标系相对于静坐标系的三个姿态角, $\begin{matrix} q_{4} 、 q_{5} 、 q_{6} \end{matrix}$ 为体坐标系相对于静坐标系沿 $\begin{matrix} X 、 Y 、 Z \end{matrix}$ 三个坐标轴的平移量。以 $\begin{matrix} ZYX \end{matrix}$ 空间齐次变换为例, 则其齐次变换矩阵表示为:

$\begin{matrix} \begin{matrix} T_{ZYX} = \\ [\begin{matrix} \begin{matrix} \cos q_{2} \cos q_{3} \\ \cos q_{2} \sin q_{3} \\ - \sin q_{2} \\ 0 \end{matrix} & \begin{matrix} E \\ G \\ \sin q_{1} \cos q_{2} \\ 0 \end{matrix} & \begin{matrix} F \\ H \\ \cos q_{1} \cos q_{2} \\ 0 \end{matrix} & \begin{matrix} q_{4} \\ q_{5} \\ q_{6} \\ 1 \end{matrix} \end{matrix}] \end{matrix} \end{matrix}$ (3)

式中: $\begin{matrix} \begin{matrix} E = - \cos q_{1} \sin q_{3} + \sin q_{1} \sin q_{2} \cos q_{3}; \\ F = \sin q_{1} \sin q_{3} + \cos q_{1} \sin q_{2} co s q_{3}; \\ G = \cos q_{1} \cos q_{3} + \sin q_{1} \sin q_{2} \sin q_{3}; \\ H = - \sin q_{1} \cos q_{3} + \cos q_{1} \sin q_{2} \sin q_{3} 。 \end{matrix} \end{matrix}$

当上平台空间各点发生位姿变化后, 利用空间变换矩阵能够实现体坐标系与静坐标系的坐标转换, 进而可得到相应的静坐标系下的坐标值。空间变换矩阵表示为:

$\begin{matrix} A' = T_{ZYX} \cdot A \end{matrix}$ (4)

综上, 上平台铰链点坐标和下平台铰链点坐标均转换到同一静坐标系下, 由此连接上、下平台铰链点的6根伸缩杆杆长可根据上、下铰链点间的距离确定。杆长向量 $\begin{matrix} L \end{matrix}$ 表达式为:

$\begin{matrix} L = T_{ZYX} \cdot A - B \end{matrix}$ (5)

进而, 对应6个伸缩杆杆长可根据求模公式计算得:

$\begin{matrix} \begin{matrix} ‖ T_{ZYX} \cdot A - B ‖= L_{i} \\ i = 1, 2, \dots, 6 \end{matrix} \end{matrix}$ (6)

2.2 非线性方程组的求解

由于多元非线性方程组求解过程复杂且耗时较长, 简单的数学计算方法已无法满足求解需求, 因此, 需借助计算机通过软件编程方法进行实现。牛顿迭代法^{[8, 9]}是求解非线性方程组的通用方法, 其对初值的选取要求较高。初值选取不当会严重影响收敛速度和误差性。因此, 采用改进的BP神经网络算法对初始值进行预估, 以提升初始值选取的合理性, 进而采用牛顿迭代法对非线性方程组进行求解。为了方便计算, 将6个连接杆的长度计算公式等效为:

$\begin{matrix} \begin{matrix} \overset{6}{\sum_{i = 1}} F_{i} (q_{1}, q_{2}, q_{3}, q_{4}, q_{5}, q_{6}) = \\ (T_{ZYX} \cdot A - B) \cdot (T_{ZYX} {\cdot A - B)}^{T} - {L_{i}}^{2} \end{matrix} \end{matrix}$ (7)

式中: $\begin{matrix} F (\cdot) \end{matrix}$ 表示假设的非线性函数。

为了求解式(7)中的6个未知参量, 需对非线性方程组(7)进行线性化处理。采用泰勒级数展开式对式(7)展开, 取线性部分:

$\begin{matrix} F_{i} (q_{j}^{(k)}) + \overset{6}{\sum_{j = 1}} (q_{j}^{(k + 1)} - q_{j}^{(k)}) \frac{\partial F_{i} (q_{j}^{(k)})}{\partial q_{j}^{(k)}} \approx 0 \end{matrix}$ (8)

根据牛顿迭代法, 可令 $\begin{matrix} (q_{j}^{(k + 1)} - q_{j}^{(k)}) = Δ q_{j}^{(k)}, \end{matrix}$ 则式(8)可以简化为:

$\begin{matrix} \begin{matrix} F_{i} (q_{j}^{(k)}, L_{i}) \approx - J^{(k)} Δ q_{j}^{(k)} \\ i = 1, 2, \dots, 6, j = 1, 2, \dots, 6 \end{matrix} \end{matrix}$ (9)

式中: $\begin{matrix} J^{(k)} \end{matrix}$ 表示为对非线性方程组(式(7))求得雅克比矩阵, 表达式为:

$\begin{matrix} J = (\begin{matrix} \frac{\partial F_{1}}{\partial q_{1}} & \dots & \frac{\partial F_{1}}{\partial q_{6}} \\ ︙ & ︙ \\ \frac{\partial F_{6}}{\partial q_{1}} & \dots & \frac{\partial F_{6}}{\partial q_{6}} \end{matrix}) \end{matrix}$ (10)

式中: $\begin{matrix} \partial F_{1} / \partial q_{1} \end{matrix}$ 为式(7)中第一个方程对未知数 $\begin{matrix} q_{1} \end{matrix}$ 的偏导数。

当 $\begin{matrix} Δ q_{j}^{(k)} = (q_{j}^{(k + 1)} - q_{j}^{(k)}) \leq ε (ε \end{matrix}$ 为设定的误差精度)时, 即 $\begin{matrix} \max (Δ q_{1,} Δ q_{2,} Δ q_{3,} Δ q_{4,} Δ q_{5,} Δ q_{6}) \leq ε, \end{matrix}$ 迭代终止, 此时可求得6个未知参量。

3 基于L-M算法的BP神经网络模型

BP神经网络对非线性函数的逼近能力以及训练网络的联想记忆和预测能力, 这些对并联机构的逆向建模都有关键性作用。因此, 提出了基于L-M算法的BP神经网络改进算法, 进一步提升算法的收敛速度和计算精度。并采用位姿反解中大量的运行数据作为训练样本, 对改进模型进行训练, 进而实现位姿正解初值补偿。

3.1 BP神经网络

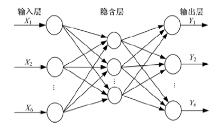
BP神经网络^[10]由输入层、隐含层和输出层三部分构成, 其中隐含层可设置为单层或多层。对于一个三层的BP神经网络可以实现任意的 $\begin{matrix} n 维到 m \end{matrix}$ 维的映射。神经网络结构图如图2所示。

	Figure Option View Download New Window
	图2 BP神经网络结构图Fig.2 Structure diagram of BP neutral network

BP神经网络中神经元输出的计算模型为:

$\begin{matrix} \begin{matrix} H = f (\overset{n}{\sum_{i = 1}} w_{ij} x_{i} - a_{j}) \\ j = 1, 2, \dots, l \end{matrix} \end{matrix}$ (11)

式中: $\begin{matrix} l \end{matrix}$ 为节点数; $\begin{matrix} f (\cdot) \end{matrix}$ 为激励函数; $\begin{matrix} w_{ij} \end{matrix}$ 为每层之间连接权值; $\begin{matrix} a_{j} \end{matrix}$ 为阈值; $\begin{matrix} H \end{matrix}$ 为神经元输出。

结合BP神经网络结构确定的两个主要因素:训练时间和网络精度。由于位姿正解初值补偿过程对求解的实时性和计算精度均有着较高要求, 因此, 选取单隐含层型网络结构, 并采用试凑法与经验公式相结合的方法来确认隐含层节点数的最大值 $\begin{matrix} n_{l}_\max \end{matrix}$ 与最小值 $\begin{matrix} n_{l}_\min 。 \end{matrix}$ 隐含层单元数选择的经验公式主要如下:

(1) $\begin{matrix} \overset{n}{\sum_{i = 0}} \end{matrix} \begin{matrix} C_{n_{l}}^{i} \end{matrix}$ > k, 其中 $\begin{matrix} k \end{matrix}$ 为样本数, $\begin{matrix} n_{i} \end{matrix}$ 为隐含层单元数, $\begin{matrix} n \end{matrix}$ 为输入单元数, $\begin{matrix} i \end{matrix}$ 为 $\begin{matrix} (0, n) \end{matrix}$ 间的常数。

(2) $\begin{matrix} n_{l} = \sqrt[]{n + m} + a, \end{matrix}$ 其中 $\begin{matrix} n_{l} \end{matrix}$ 为隐含层单元数, $\begin{matrix} n \end{matrix}$ 为输入单元数, $\begin{matrix} m \end{matrix}$ 为输出单元数, $\begin{matrix} a \end{matrix}$ 为 $\begin{matrix} (1, 10) \end{matrix}$ 间的常数。结合本神经网络训练模型可得, 输入为6根杆的杆长, 因此 $\begin{matrix} n \end{matrix}$ 为6; 输出为6个位姿量 $\begin{matrix} (q_{1}, q_{2}, \dots, q_{6}), \end{matrix}$ 因此 $\begin{matrix} m \end{matrix}$ 为6, 根据计算隐含层节点数经验公式可预测隐含层节点数的最大值为3, 最小值为18。

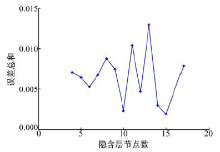
在选取训练集相同情况下, 采用网络收敛速度和计算精度为评价准则, 选取收敛速度快且计算精度高的隐含层结构作为选取的结构。试验如下, 在选取训练集相同情况下, 依据经验公式得到的隐含层节点数范围, 依次选取不同的隐含层节点, 得出对应的神经网络预测误差总和。如图3所示, 在最大迭代次数为1000次、最终迭代终止目标为4× 10^-7、学习率为0.1的试验条件下, 分析不同隐含层节点数对误差总和的影响。从图3中可看出, 神经网络误差总和随隐含层节点数的增加呈现出先增加后减少的趋势。

	Figure Option View Download New Window
	图3 隐含层节点数与误差总和的关系Fig.3 Relationship between node numbers of hidden layer and sum error

在BP神经网络结构和相应的权值、阈值相同的情况下, 选取不同的隐含层和输出层激励函数进行试验, 选出最优激励函数。试验如下:当随机选取100组运动状态的杆长伸缩量作为神经网络的输入值时, 利用选取不同的隐含层和输出层函数得到的神经网络预测其位姿变化值, 并与期望值进行对比, 得出BP神经网络预测误差百分比和、均方误差与输出隐含层及输出层节点激励函数的关系, 如表1所示。从表1中可以得出:网络预测精度较好的是1号和2号函数组合, 预测误差百分比总和分别为0.0775、0.0630; 迭代次数和训练时间较短的是1, 4, 8, 9函数组合。选取logsig函数作为神经网络激励函数能够提高计算精度, 但算法迭代次数较多, 训练时间较长, 且占用CPU非常大, 因此不做为最理想的隐含层激励函数。而由于tansig函数作为隐含层激励函数时收敛速度满足计算要求, purelin线性函数能够对误差做出快速响应, 加快训练速度。因此, 本文选择tansig函数作为隐含层激励函数, purelin函数作为输出层激励函数。

表1 选择不同的隐含层和输出层激励函数的试验结果 Table 1 Test results of transfer function based on different hidden layer and output layer

3.2 基于L-M算法位姿正解初值补偿器的设计

位姿正解初值补偿器主要基于L-M算法改进的BP神经网络, 选取三层神经网络结构, 根据实际模型输入、输出需求设置:输入层为6个神经元, 隐含层为15个神经元, 输出层为6个神经元。位姿正解初值补偿器设计思想为将 $\begin{matrix} n \end{matrix}$ 个输入样本 $\begin{matrix} X = [x^{1}, x^{2}, \dots, x^{n}] \end{matrix}$ 与输出样本 $\begin{matrix} Y = [y^{1}, y^{2}, \dots, y^{n}] \end{matrix}$ 一一对应, 并通过对比实际输出 $\begin{matrix} H = [H^{1}, H^{2}, \dots, H^{n}] \end{matrix}$ 与目标输出期望 $\begin{matrix} Y \end{matrix}$ 的差值将误差反向传递到神经网络值, 从而使相应连接权值进行修正, 进而使误差处于容忍误差集合范围之内。

L-M算法主要采用模型函数 $\begin{matrix} F \end{matrix}$ (式(7)中非线性函数)对待估参数向量 $\begin{matrix} Y \end{matrix}$ 在其领域内做线性近似, 忽略掉二阶以上的导数项, 从而转化为线性最小二乘问题, 它具有收敛速度快等优点, 能够优化BP神经网络。

$\begin{matrix} \begin{matrix} E = \frac{1}{2} \sum \sum (d_{kj} - y_{kj})^{2} = \\ \frac{1}{2} \sum_{k} (ε^{k})^{2} = \frac{1}{2} ‖ ε ‖^{2} \end{matrix} \end{matrix}$ (12)

式中: $\begin{matrix} E \end{matrix}$ 为误差平方和; $\begin{matrix} d_{kj} \end{matrix}$ 为系统期望输出值; $\begin{matrix} y_{kj} \end{matrix}$ 为输出层第 $\begin{matrix} k \end{matrix}$ 个神经元的实际输出。

从第 $\begin{matrix} i \end{matrix}$ 次迭代到第 $\begin{matrix} i + 1 \end{matrix}$ 次迭代计算时, 采用关于 $\begin{matrix} X \end{matrix}$ 的雅克比矩阵 $\begin{matrix} J, \end{matrix}$ 从而得到误差函数公式:

$\begin{matrix} \begin{matrix} E = \frac{1}{2} ‖ ε (X^{i}) + J (X^{i + 1} - X^{i}) ‖^{2} + \\ μ ‖ X^{i + 1} - X^{i} ‖^{2} \end{matrix} \end{matrix}$ (13)

通过Matlab编程软件计算每次迭代之后的误差总和是否处于计算误差容忍范围内。如果不在范围之内, 则一直迭代, 直到接近甚至达到最优误差值则停止迭代。在训练过程中, 改进的神经网络能够通过不断地迭代对网络自身参数进行调整和修正, 以满足系统计算需求, 从而实现对非线性系统的系统辨识与函数关系映射。

3.3 基于L-M算法的BP神经网络模型构建

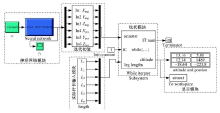
BP神经网络本身收敛速度较慢, 迭代次数较多, 预测精度不高, 基于L-M的BP神经网络算法的Simulink建模仿真如图4所示, 其训练好的神经网络得出的迭代初值能够提高位姿正解模型的动态响应速度与鲁棒性。

	Figure Option View Download New Window
	图4 Simulink建模仿真分析Fig.4 Simulink modeling and simulating analysis

利用L-M算法与BP神经网络的融合算法, 对六自由度位姿正解的迭代初值进行非线性校正, 需选取大量的学习样本。采用Simulink搭建的位姿反解模型与试验搭建的SolidWorks模型相结合的方法选取大量试验样本, 样本选取在运动平台工作空间之内, 且保证样本空间中位姿值处于变化范围之内, 且满足杆长伸缩量的最大、最小值限定。Simulink反解模型求解出体坐标系下的位姿值与对应伸缩杆杆长值作为样本数据值。同时借助SolidWorks模型进行验证, 保证选取样本值的可靠性与可达性。样本训练过程如下:

(1)初始化改进神经网络的阈值与权值, 利用Matlab中的rand和sort函数将1000组输入、输出数据顺序随机, 保证训练数据的有效性。选取900组数据作为训练数据, 剩下的100组数据作为测试数据。

(2)利用Matlab中mapminmax函数将全部样本数据进行归一化处理。由于位姿反解的角度弧度值应小于0.5, 位移值在100~500 mm左右波动, 角度值与位移值之间存在三个数量级, 为了防止预测计算过程中出现“ 大数吃小数” 的问题, 需先对选取的数据进行归一化处理, 进而提升训练网络的计算精度。

(3)预设期望值与输出值误差为4× 10^-10, 当计算网络误差模型输出误差达到规定要求时, 停止训练。

4 试验验证

为了校验本文算法的可行性, 分别采用预测模型的3种算法, 即BFGS拟牛顿算法、SCG量化共轭梯度算法、GDA梯度下降自适应算法, 作为基于L-M算法的BP神经网络算法的对比算法进行实验对比。

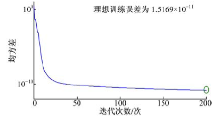
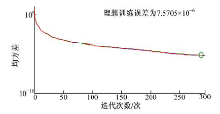
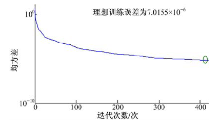
如图5所示, 基于L-M算法的BP神经网络训练模型训练时耗时19 s, 迭代次数为250次, 预测输出对比期望数据误差为1.5264× 10^-11; 如图6所示, 基于BFGS拟牛顿算法的神经网络训练时耗时7 s, 训练迭代次数为219次, 误差为7.3758× 10^-6; 如图7所示,

	Figure Option View Download New Window
	图5 L-M算法误差性能分析Fig.5 Error performance analysis of L-M algorithm

	Figure Option View Download New Window
	图6 BFGS拟牛顿算法误差性能分析Fig.6 Error performance analysis of BFGS quasi-Newton backpropagation

	Figure Option View Download New Window
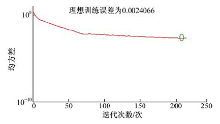	图7 GDA自适应变学习率梯度下降算法的误差性能分析Fig.7 Error performance analysis of gradient descent with adaptive learning rate backpropagation

	Figure Option View Download New Window
	图8 SCG量化共轭梯度算法的误差性能分析Fig.8 Error performance analysis of scaled conjugate gradient backpropagation

	Figure Option View Download New Window
	图9 角度值的网络预测误差Fig.9 Network prediction error of angle value

	Figure Option View Download New Window
	图10 角度值的网络预测误差百分比Fig.10 Network prediction error percentage of angle value

	Figure Option View Download New Window
	图11 位移值的网络预测误差Fig.11 Network prediction error of displacement value

	Figure Option View Download New Window
	图12 位移值的网络预测误差百分比Fig.12 Network prediction error percentage of displacement value

基于GDA自适应变学习率梯度下降算法的神经网络训练耗时5 s, 训练迭代次数为154次, 误差为0.00486; 如图8所示, 基于SCG量化共轭梯度算法的神经网络训练时耗时3 s, 训练迭代次数为460次, 误差为6.2869× 10^-6。对比上述4种算法, 可得基于L-M算法的BP神经网络误差最小, 甚至可以考虑在线训练网络, 但迭代次数和耗时都很高。SCG算法耗时很短, 但迭代次数较长, 误差性能较L-M算法较低。

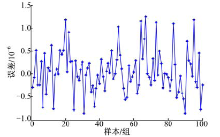
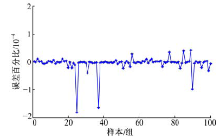
图9~图12均为基于L-M算法神经网络模型的预测误差。图9和图11能够反映100组测试数据中每组数据的预测误差, 易知测试数据中角度值网络预测误差均低于1.5× 10^-6, 角度值单位为rad; 位移值的网络预测误差均低于1× 10^-3, 位移值单位为mm。图10、图12能够反映100组预测数据误差百分比, 可知角度值误差百分比低于2× 10^-4, 位移值误差百分比低于4× 10^-4, 均满足实际精度要求。

5 结束语

本文针对牛顿迭代法对初值选取的依赖的问题, 提出基于L-M算法的BP神经网络位姿正解初值补偿方法, 通过与BFGS拟牛顿算法、SCG量化共轭梯度算法、GDA梯度下降自适应算法所建立的BP神经网络模型对比分析可知, 基于L-M算法的神经网络理想训练误差性能可达到1.5264× 10^-11, 且绕轴旋转角度值网络预测误差均低于1.5× 10^-6, 轴向平移位移值的网络预测误差均低于1× 10^-3。这说明作者提出的改进模型能够有效提升初值计算的准确性, 并缩短计算时间。本文的研究为正交Stewart六自由运动平台位姿控制、故障恢复及工作空间分析等奠定了基础, 研究方法不仅仅适用于正交Stewart六自由度运动平台, 且适用于其他并联机构。六自由度运动平台实际运动的车端位姿检测装置的提出, 可实现车端在运动过程中的位姿检测, 从而为新车型的车端研究提供理论依据。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	程世利, 吴洪涛, 王超群, 等. 基于正交补的6-3 Stewart并联机构运动学正解[J]. 中国机械工程, 2011, 22(5): 505-508. Cheng Shi-li, Wu Hong-tao, Wang Chao-qun, et al. Forward kinematics analysis of 6-3 Stewart parallel mechanisms based on orthogonal complement method[J]. Chinese Journal of Mechanical Engineering, 2011, 22(5): 505-508. [本文引用:1]
[2]	李立, 张剑, 陈永, 等. 同伦迭代法的研究及其应用于机构学问题的求解[J]. 西南交通大学学报: 自然科学版, 2000, 35(1): 57-60. Li Li, Zhang Jian, Chen Yong, et al. On the homo-topy iteration method and its application in the mechanism problems[J]. Journal of Southwest Jiaotong University(Natural Science), 2000, 35(1): 57-60. [本文引用:1]
[3]	Yu Y K. Kinematic geometry, dynamics and control of parallel manipulator[D]. Hong Kong: Hong Kong University of Science and Technology, 2002: 35-49. [本文引用:1]
[4]	Gough V E, Whitehall S G. Universal Type Test Machine[C]//Procedding of FISITA International Technical Congress, Bangkok, Thailand , 1962: 117-137. [本文引用:1]
[5]	Nanua P, Waldron K J, Murthy V. Direct kinematic solution of a Stewart platform[J]. IEEE Transactions on Robotics and Automation, 1990, 6(4): 438-444. [本文引用:1]
[6]	姜虹, 贾嵘, 董洪智, 等. 六自由度并联机器人位置正解的数值解法[J]. 上海交通大学学报, 2000, 34(3): 351-353. Jiang Hong, Jia Rong, Dong Hong-zhi, et al. Positional solution of a six-degree of freedom parallel robot[J]. Journal of Shanghai Jiaotong University, 2000, 34(3): 351-353. [本文引用:1]
[7]	车林仙, 何兵, 易建, 等. 对称结构Stewart机构位置正解的改进粒子群算法[J]. 农业机械学报, 2008, 39(10): 158-163. Che Lin-xian, He Bing, Yi Jian, et al. Improved particle swarm optimization for forward positional analysis of symmetrical Stewart parallel manipulators[J]. Transactions of the Chinese Society for Agriculture, 2008, 39(10): 158-163. [本文引用:1]
[8]	Gallardo J, Lesso R, Rico J M, et al. The kinematics of modular spatial hyper-redundant manipulators formed from RPS-type limbs[J]. Robotics and Autonomous Systems, 2011, 58(1): 12-21. [本文引用:1]
[9]	Tarokh M, Keerthik K, Lee M. Classification and characterization of inverse kinematics solutions for anthropomorphic manipulators[J]. Robotics and Autonomous Systems, 2010, 58(1): 115-120. [本文引用:1]
[10]	沈花玉, 王兆霞, 高成耀, 等. BP神经网络隐含层单元数的确定[J]. 天津理工大学学报, 2008, 24(5): 13-15. Shen Hua-yu, Wang Zhao-Xia, Gao Cheng-yao, et al. Determining the number of BP neural network hidden layer units[J]. Journal of Tianjin University of Technology, 2008, 24(5): 13-15. [本文引用:1]

2011

0.0

. 2011, 22(5):505-508

Forward kinematics analysis of 6-3 Stewart parallel mechanisms based on orthogonal complement method

基于正交补的6-3 Stewart并联机构运动学正解

Cheng Shi-li , Wu Hong-tao , Wang Chao-qun

程世利, 吴洪涛, 王超群

1.Nanjing University of Aeronautics & Astronautics, Nanjing, 210016 2.Nanjing Agricultural University, Nanjing, 210031

This paper presented a new analytical method to study the forward kinematics analysis of 6-3 Stewart parallel mechanisms. Analyzing the coupling relationships among the position and orientation variables of the moving platform, additional useful information was obtained, thus eleven compatible algebra equations used to solve this problem were obtained. The orthogonal complement method was used to eliminate the redundant variables, the forward kinematics of 6-3 Stewart parallel mechanisms can be expressed as an eight order equation in the end. Finally a specific example was introduced to verify the method offered herein. 

提出了一种研究6-3 Stewart并联机构运动学正解问题的新方法。通过分析动平台位姿变量之间的耦合关系,增加了一些有用的信息,得到了用于解决这一问题的11个相容方程。使用正交补方法进行消元,最终可以将6-3 Stewart并联机构运动学正解问题表达成一个一元八次方程。最后通过一个实例验证了该方法的正确性。  

... 位姿正解^[1]的求解对于六自由度工作空间分析、机构设计以及机构在故障中恢复均有重要作用,因此,合理有效快速的位姿正解求解方法是十分必要的 ...

2000

0.0

... 目前,位姿正解求解方法主要包括解析法^[2,3,4]和数值法^[5]两种 ...

2002

0.0

... 目前,位姿正解求解方法主要包括解析法^[2,3,4]和数值法^[5]两种 ...

1962

0.0

... 目前,位姿正解求解方法主要包括解析法^[2,3,4]和数值法^[5]两种 ...

1990

0.0

... 目前,位姿正解求解方法主要包括解析法^[2,3,4]和数值法^[5]两种 ...

2000

0.0

... 数值法采用迭代法求解,对迭代初值的要求较高,初值选取不当则会致使迭代无法收敛^[6],进而导致无法获取正确解 ...

2008

0.0

... 借助SolidWorks软件和Simulink仿真平台建立六自由度平台位姿反解模型,将位姿反解模型中的位姿量及对应的杆长伸缩量,作为改进BP神经网络模型^[7]训练样本 ...

2011

0.0

... 牛顿迭代法^[8,9]是求解非线性方程组的通用方法,其对初值的选取要求较高 ...

2010

0.0

... 牛顿迭代法^[8,9]是求解非线性方程组的通用方法,其对初值的选取要求较高 ...

2008

0.0

... 1 BP神经网络BP神经网络^[10]由输入层、隐含层和输出层三部分构成,其中隐含层可设置为单层或多层 ...