驱动冗余重型并联机构的动力学性能

引用本文

许金凯, 王煜天, 张世忠. 驱动冗余重型并联机构的动力学性能. 2017, 47(4): 1138-1143
XU Jin-kai, WANG Yu-tian, ZHANG Shi-zhong. Dynamic characteristics of a heavy duty parallel mechanism with actuation redundancy. Journal of Jilin University Engineering and Technology Edition, 2017, 47(4): 1138-1143 复制到剪切板

Permissions

驱动冗余重型并联机构的动力学性能

许金凯^1,², 王煜天¹, 张世忠³

1.长春理工大学机电工程学院,长春 130022

2. 长春理工大学精密制造及检测技术国家地方联合工程实验室,长春 130022

3. 吉林大学机械科学与工程学院,长春 130022

通讯作者：张世忠(1983-),男,讲师,博士.研究方向:原位力学测试技术与仪器.E-mail:szzhang@jlu.edu.cn

作者简介:许金凯(1978-),男,副研究员,博士生导师.研究方向:精密超精密加工与检测技术及其装备研制.E-mail:xujinkai2000@163.com

基金:吉林省科技创新人才培育计划青年科研基金项目(20160520067JH).

摘要

针对重型并联机构构型不足的问题,提出了一种适合重载加工的2自由度龙门式驱动冗余并联机构。首先,在运动学分析的基础上,利用虚功原理建立了系统的动力学模型。其次,以动力学模型中驱动力的范数最小为目标,对驱动力进行优化,并给出了一种加速度性能评价指标。最后,基于驱动力优化方法以及加速性能评价指标分析比较了在相同运动条件下该冗余重型并联机构与其对应的非冗余并联机构的动力学性能。本文研究结果对其他重型关联机构的构型设计以及加速度评价具有重要的参考价值。

关键词: 自动控制技术; 并联机构; 虚功原理; 动力学; 驱动冗余; 性能评价

中图分类号:TP242 文献标志码:A 文章编号:1671-5497(2017)04-1138-06

Dynamic characteristics of a heavy duty parallel mechanism with actuation redundancy

XU Jin-kai^1,², WANG Yu-tian¹, ZHANG Shi-zhong³

1.College of Mechanical and Electric Engineering, Changchun University of Science and Technology, Changchun 130022,China

2.National and Local Joint Engineering Laboratory of Precision Manufacturing and Measurement Techniques, Changchun University of Science and Technology, Changchun 130022,China

3.College of Mechanical Science and Engineering, Jilin University, Changchun 130022,China

Abstract

The types of heavy-duty parallel mechanisms are not sufficient for industrial applications. A two degree of freedom (2DOF) heavy-duty parallel mechanism with actuation redundancy is proposed. The kinematics of the mechanism is analyzed and the dynamic model is derived using the principle of virtual work. The driving force is optimized based on the force optimization method. An evaluation method of the acceleration is given. The acceleration of the redundantly actuated parallel mechanism is compared with its corresponding non-redundant parallel mechanism. It is proved that the proposed parallel mechanism is useful for industry and the acceleration evaluation index is also helpful for the acceleration evaluation of other parallel mechanisms.

Keyword: automatic control technology; parallel mechanism; principle of virtual work; dynamics; actuation redundancy; performance evaluation

Show Figures

0 引言

并联机构具有刚度高、惯量小、动态特性好等优点, 在高速、大承载场合, 与串联机构相比具有明显优势。因此, 并联机构得到了广泛的关注, 出现了各种多自由度和少自由度并联机构构型, 一些并联机构成功应用于飞行模拟器、数控机床、喷涂机器人等领域^{[1, 2]}。特别是Delta并联机器人、Z3并联机构主轴头的成功应用^[3], 增强了研究人员对并联机构工业应用的信心。然而, 适用于重型加工的并联机构构型相对较少, 限制了并联机构的广泛应用和推广^[4]。

动力学是并联机构的重要性能, 特别是并联机构应用于数控机床领域, 对其动态特性要求更高^[5]。由于并联机构的闭环特性, 并联机构动力学具有高度耦合性、强烈非线性等特点, 动力学模型复杂。对于驱动冗余并联机构, 其动力学方程是静不定的, 对于给定的控制输入, 存在着多种可能的驱动力/力矩向量, 必须协调好各关节的驱动力输入, 否则会导致较大的内力破坏机构。这就涉及到对驱动冗余并联机构动力学的优化问题。此外, 为了衡量并联机构动力学性能的优劣, 需要适当的评价方法和指标。目前, 并联机构的动力学性能评价指标主要是沿用传统的串联机构动力学性能评价指标, 还缺少驱动冗余并联机构的动力学性能评价方法及指标^{[6, 7]}。

本文首先提出一种适合重型加工的龙门式并联机构构型, 然后建立其运动学模型。基于运动学模型, 利用虚功原理建立系统的动力学模型, 并对该机构的驱动力进行优化。进一步, 基于动力学模型, 给出一种适合非冗余并联机构和冗余并联机构的动力学性能评价指标。最后, 通过仿真比较了冗余和非冗余并联机构的动力学性能。

1 运动学性能分析

1.1 机构描述

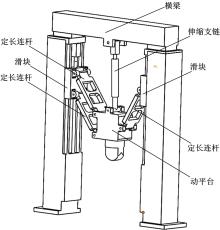
图1为具有2个平动自由度的重型并联机构, 该并联机构具有龙门架式结构, 安装在左、右两个立柱上的滑块分别由伺服电机通过滚珠丝杠驱动; 左边滑块通过两个定长连杆与动平台连接, 右边滑块通过一个定长连杆与动平台连接。两个滑块沿固定在立柱上的导轨可以上下运动, 通过定长连杆带动动平台实现2个自由度的平动, 此外一个带主动驱动的伸缩支链也连接到动平台, 从而构成驱动冗余并联机构。

	Figure Option View Download New Window
	图1 重型冗余并联机构三维图Fig.1 3D of a heavy-duty planar parallel mechanism with actuation redundancy

由于伸缩支链可以对动平台施加竖直方向的力, 因此添加伸缩支链可以使机构具有刚度高、负载能力强等优点。另外, 当左边两个定长连杆与右边定长连杆共线时机构处于奇异位形, 添加伸缩支链可以避免这类奇异位形。联合该冗余并联机构、两自由度铣头和沿垂直 $\begin{matrix} XY \end{matrix}$ 平面移动的工作台, 可以组成一台五轴混联机床, 特别适合于重载加工等领域应用。

1.2 运动学及加速度

图2是重型驱动冗余并联机构的运动学模型, 在机座上两个立柱的中心点O处建立全局坐标系O-XY, 在动平台的中心处建立动坐标系O'-X'Y'。为了运动学和动力学建模方便, 在D_i 处分别建立坐标系D_i-xy和D_i-x'y', 其中x和y轴分别与X和Y轴平行, x'轴沿着连杆D_i C_i的杆长方向。

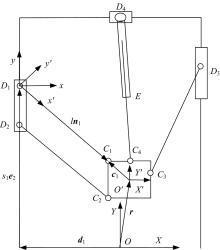	Figure Option View Download New Window
	图2 冗余并联机床结构分析图Fig.2 Structure diagram of heavy-duty planar parallel mechanism with actuation redundancy

定义点O'在全局坐标系O-XY中的位置矢量为r=[xy]^T, 则连杆C_iD_i的限制方程可以表示为:

$\begin{matrix} r + c_{i} = d_{i} + s_{i} e_{2} + l n_{i}, i = 1, 2, 3 (1) \end{matrix}$

式中:c_i 表示点C_i 在动坐标系O'-X'Y'中的位置矢量, c_i=[c_ixc_iy]^T; d_i表示从点O到立柱沿水平方向的位置矢量; s_i表示D_i点在O-XY坐标系中的Y坐标值; e₂=[01]^T; l和n_i分别表示连杆C_iD_i的长度和单位矢量。

伸缩连杆 $\begin{matrix} C_{4} D_{4} \end{matrix}$ 的限制方程可以表示为:

$\begin{matrix} r + c_{4} = d_{4} + (l_{41} + l_{42}) n_{4} (2) \end{matrix}$

式中:c₄ 表示点C₄ 在动坐标系O'-X'Y'中的位置矢量, c₄=[c₄xc_4y]^T; d₄表示从点O到D₄ 的位置矢量; l₄₁ 和l₄₂ 分别表示伸缩连杆C₄D₄ 的上半部分和下半部分的长度; n₄表示伸缩连杆C₄ D₄的单位矢量。

对方程(1)两边同时取范数, 可以得到:

$\begin{matrix} s_{i} = r^{T} e_{2} + \sqrt[]{{(r^{T} e_{2})}^{2} - {|r + c_{i} - d_{i}|}^{2} + l^{2}} (3) \end{matrix}$

相应地可以得到连杆 $\begin{matrix} C_{i} D_{i} \end{matrix}$ 的单位矢量为:

$\begin{matrix} n_{i} = [\begin{matrix} n_{ix} \\ n_{iy} \end{matrix}] = \frac{r + c_{i} - d_{i} - s_{i} e_{2}}{l} (4) \end{matrix}$

式中:n_ix 和n_iy 分别表示n_i 的x和y方向分量。

基于方程(2), 伸缩连杆 $\begin{matrix} C_{4} D_{4} \end{matrix}$ 的长度和单位矢量可以表示为:

$l_{41} + l_{42} = |r + c_{4} - d_{4}| (5)$

$\begin{matrix} \begin{matrix} n_{4} = [\begin{matrix} n_{4 x} \\ n_{4 y} \end{matrix}] = \frac{r + c_{4} - d_{4}}{l_{41} + l_{42}} (6) \end{matrix} \end{matrix}$

假设r'_ci表示连杆C_iD_i 质心相对于坐标系D_i-x'y'的位置矢量, 则连杆C_iD_i 质心相对于坐标系D_i-xy的位置矢量可以表示为:

$\begin{matrix} r_{ci} = [\begin{matrix} r_{cxi} \\ r_{cyi} \end{matrix}] = R \cdot r'_{c i} i = 1, 2, 3 (7) \end{matrix}$

式中:r_cxi 和r_cyi 表示r_ci 在x和y方向分量; R表示从坐标系D_i-x'y'到坐标系D_i-xy的旋转变换矩阵。

连杆C_iD_i 质心在全局坐标系O-XY中的位置矢量为:

$\begin{matrix} r_{gi} = [\begin{matrix} r_{gix} \\ r_{giy} \end{matrix}] = d_{i} + s_{i} e_{2} + r_{ci} (8) \end{matrix}$

伸缩连杆C₄D₄ 的上部分D₄ E和下部分EC₄的质心位置可以表示为:

$r_{g 41} = [\begin{matrix} r_{g 41 x} \\ r_{g 41 y} \end{matrix}] = d_{4} + \frac{l_{41} n_{4}}{2} (9)$

$\begin{matrix} \begin{matrix} r_{g 42} = [\begin{matrix} r_{g 42 x} \\ r_{g 42 y} \end{matrix}] = d_{4} + (l_{41} + \frac{l_{42}}{2}) n_{4} (10) \end{matrix} \end{matrix}$

1.3 加速度分析

对方程(1)二次求导, 可以得到:

$\begin{matrix} \overset{\cdot \cdot}{r} = {\overset{\cdot \cdot}{s}}_{i} e_{2} + l ε_{i} [\begin{matrix} - n_{iy} \\ n_{ix} \end{matrix}] - l ω_{i}^{2} n_{i} (11) \end{matrix}$

式中: $\begin{matrix} ω_{i} 和 ε_{i} \end{matrix}$ 分别表示连杆 $\begin{matrix} C_{i} D_{i} \end{matrix}$ 的角速度和角加速度。

基于方程(11), 可以得到滑块的加速度和连杆 $\begin{matrix} C_{i} D_{i} \end{matrix}$ 的角加速度为:

$\begin{matrix} \begin{matrix} {\overset{\cdot \cdot}{s}}_{i} = \frac{{n^{T}}_{i} \overset{\cdot \cdot}{r} + l ω_{i}^{2}}{{n^{T}}_{i} e_{2}} (12) \\ ε_{i} = \frac{\overset{\cdot \cdot}{r} - {\overset{\cdot \cdot}{s}}_{i} e_{2}}{l} \cdot [\begin{matrix} - n_{iy} \\ n_{ix} \end{matrix}] (13) \end{matrix} \end{matrix}$

对方程(8)二次求导, 可以得到连杆 $\begin{matrix} C_{i} D_{i} \end{matrix}$ 质心的加速度为:

$\begin{matrix} {\overset{\cdot \cdot}{r}}_{gi} = {\overset{\cdot \cdot}{s}}_{i} e_{2} + {\overset{\cdot \cdot}{r}}_{ci} (14) \end{matrix}$

式中: $\begin{matrix} {\overset{\cdot \cdot}{r}}_{gi} \end{matrix}$ 和 $\begin{matrix} {\overset{\cdot \cdot}{r}}_{ci} \end{matrix}$ 分别表示连杆𝐶_𝑖𝐷_𝑖质心在坐标系𝑂-𝑋𝑌和𝐷_𝑖-𝑋𝑌中的加速度。

对方程(9)和(10)二次求导, 可以得到伸缩连杆C₄D₄ 的上部分D₄ E和下部分EC₄质心的加速度分别为:

${\overset{\cdot \cdot}{r}}_{g 41} = \frac{l_{41} ε_{4}}{2} [\begin{matrix} - n_{4 y} \\ n_{4 x} \end{matrix}] - \frac{l_{41} ω_{4}^{2} n_{4}}{2} (15)$

$\begin{matrix} \begin{matrix} {\overset{\cdot \cdot}{r}}_{g 42} = \frac{{\overset{\cdot \cdot}{l}}_{42}}{2} n_{4} + {\overset{\cdot}{l}}_{42} ω_{4} [\begin{matrix} - n_{4 y} \\ n_{4 x} \end{matrix}] + (l_{41} + \frac{l_{42}}{2}) \times \\ ε_{4} [\begin{matrix} - n_{4 y} \\ n_{4 x} \end{matrix}] - (l_{41} + \frac{l_{42}}{2}) ω_{4}^{2} n_{4} \\ (16) \end{matrix} \end{matrix}$

式中:ω ₄ 和ε ₄ 分别表示伸缩连杆C₄D₄的角速度和角加速度。

2 动力学建模

2.1 杆件受力分析

本文利用虚功原理建立重型并联机构的动力学模型。利用虚功原理建模, 需要求运动构件的偏速度和偏角速度矩阵。偏速度和偏角速度矩阵反映了机构各个杆件的速度、角速度和末端执行器速度、角速度的映射关系, 可以表示为:

$H_{i} = {[\begin{matrix} \frac{\partial v_{ix}}{\partial r_{x}} & \frac{\partial v_{ix}}{\partial r_{y}} \\ \frac{\partial v_{iy}}{\partial r_{x}} & \frac{\partial v_{iy}}{\partial r_{y}} \end{matrix}]}^{T} (17)$

$\begin{matrix} \begin{matrix} G_{i} = {[\begin{matrix} \frac{\partial ω_{i}}{\partial r_{x}} & \frac{\partial ω_{i}}{\partial r_{y}} \end{matrix}]}^{T} (18) \end{matrix} \end{matrix}$

式中: $\begin{matrix} H_{i} 和 G_{i} \end{matrix}$ 分别表示偏速度和偏角速度矩阵。根据式(17)(18)就可以分别求出各个运动部件相对于其关键点的偏速度矩阵和偏角速度矩阵。

在求出了运动构件的偏角度矩阵和相对于关键点的偏速度矩阵之后, 需要推导各个运动构件相对于关键点的惯性力和惯性力矩。这里利用牛顿-欧拉方程求解各个运动构件惯性力和惯性力矩。规定m_i (i=1, 2, 3)为支链C_iD_i 质量; m₄₁ 为伸缩支链C₄D₄上半部分B₄ C的质量; m₄₂为伸缩支链C₄D₄下半部分CA₄ 的质量; m_s1 为左滑块质量; m_s2 为右滑块质量; M为动平台质量; I_i(i=1, 2, 3)为支链C_iD_i 关于D_i 点的转动惯量; I₄₁ 为伸缩支链C₄D₄ 上半部分D₄E关于D₄ 点的转动惯量; I₄₂为伸缩支链C₄D₄下半部分EC₄关于C₄点的转动惯量; , g=[0-9.81]^T为重力加速度。作用在支链C_iD_i上的力及对D_i点的力矩为:

$\begin{matrix} \{\begin{matrix} F_{i} = m_{i} (g - {\overset{\cdot \cdot}{r}}_{gi} - {\overset{\cdot \cdot}{s}}_{i} e_{2}) \\ M_{i} = I_{i} ε_{i} + m_{i} {(g - {\overset{\cdot \cdot}{r}}_{gi} - {\overset{\cdot \cdot}{s}}_{i} e_{2})}^{T} [\begin{matrix} - r_{giy} \\ r_{gix} \end{matrix}] \end{matrix} (19) \end{matrix}$

作用在伸缩支链C₄D₄上的合力和对D₄点的力矩可以表示为:

$\begin{matrix} \{\begin{matrix} F_{4 i} = m_{4 i} (g - {\overset{\cdot \cdot}{r}}_{g 4 i}) \\ M_{4 i} = I_{4 i} ε_{4} + m_{4 i} {(g - {\overset{\cdot \cdot}{r}}_{g 4 i})}^{T} [\begin{matrix} - r_{g 4 iy} \\ r_{g 4 ix} \end{matrix}] \end{matrix} (20) \end{matrix}$

作用在滑块上的合力和对 $\begin{matrix} D_{i} \end{matrix}$ 点的力矩为:

$\begin{matrix} \{\begin{matrix} F_{si} = m_{si} (g - {\overset{\cdot \cdot}{s}}_{i} e_{2}) \\ M_{si} = 0 \end{matrix} (21) \end{matrix}$

作用在动平台上的合力和对其质心的力矩为:

$\begin{matrix} \{\begin{matrix} F_{R} = M (g - \overset{\cdot \cdot}{r}) \\ M_{R} = 0 \end{matrix} (22) \end{matrix}$

2.2 驱动力优化

联合式(17)~(22), 由虚功原理得到:

$\begin{matrix} J^{T} Π + Π_{0} = 0 (23) \end{matrix}$

式中:J表示雅可比矩阵; H=[τ ₁τ ₂τ ₃]^T, 其中τ ₁ 、τ ₂ 、τ ₃ 分别表示左滑块、右滑块和伸缩支链C₄ D₄的驱动力; Π ₀= $\begin{matrix} \overset{3}{\sum_{i = 1}} \end{matrix}$ (H_iF_i+G_iM_i)+ $\begin{matrix} \overset{2}{\sum_{i = 1}} \end{matrix}$ (H₄_iF₄_i+G₄_iM₄_i)+ $\begin{matrix} \overset{2}{\sum_{i = 1}} \end{matrix}$ (H_siF_si+G_siM₅_i)+(H_RF_R+G_RM_R), 其中H_4i 为伸缩支链C₄D₄ 相对于D₄点的偏速度矩阵, G_4i为伸缩支链C₄D₄ 的偏角速度矩阵, H_si 和G_si 为滑块的偏速度矩阵和偏角速度矩阵, H_R 和G_R为动平台的偏速度矩阵和偏角速度矩阵。

从方程(23)可以列出2个与 $\begin{matrix} τ_{1} 、 τ_{2} 、 τ_{3} \end{matrix}$ 有关的独立方程, 但有3个未知数, 因此需要对驱动力进行优化。以驱动力为优化对象, 每个伺服电机提供的驱动力的平方之和为优化目标, 即优化过程中最小化 $\begin{matrix} \sqrt[]{τ_{1}^{2} + τ_{2}^{2} + τ_{3}^{2}} 。 \end{matrix}$ 在所有满足方程(23)的解空间中, 范数最小的解为:

$\begin{matrix} Π = - J {(J^{T} J)}^{- 1} Π_{0} (24) \end{matrix}$

归一化处理后, 可以得到:

$\begin{matrix} Π = M (r) \overset{\cdot \cdot}{r} + C (r, \overset{\cdot}{r}) + G (r) (25) \end{matrix}$

式中:M(r)为惯性矩阵; $C (r, \overset{\cdot}{r})$ 为离心力和科氏力矢量; G(r)为重力矢量。

2.3 加速度评价指标

动力学性能是评价并联机构加减速特性的重要指标, 在动力学方程中影响驱动力和加减速特性的因素有惯量因素、速度项因素、重力项因素, 其中与加速度项有关的惯量因素项起主导作用。为了更直接地比较机构的加减速特性, 省略式中的速度项、重力项和外力项, 对式(25)化简可得到:

$\begin{matrix} \overset{\cdot \cdot}{r} \approx {(M (r))}^{+} Π = NΠ (26) \end{matrix}$

式中: N为惯性矩阵M(r)的M-P广义逆。

目前, 还缺少并联机构加速度性能评价指标。文献[8]利用最大奇异值和最小奇异值的调和平均数HMIM作为动力学评价指标。其优势在于, 对于调和平均数只有在最大奇异值σ _max和最小奇异值σ _min都满足比较大时HMIM的值才会较大, 保证机构具有良好的各项同性的同时实现较好的加速性能。因此这里利用HMIM指标评价机构加速性能, 该指标为:

$\begin{matrix} η_{HMIM} = \frac{2}{\frac{1}{σ_{\max}} + \frac{1}{σ_{\min}}} (27) \end{matrix}$

式中:σ _max 和σ _min 分别为矩阵N的最大和最小奇异值。

3 仿真验证

3.1 冗余和非冗余并联机构驱动力比较

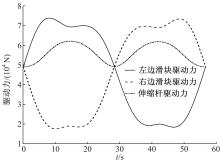
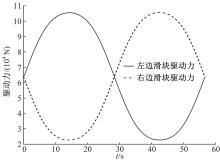
这里假设该并联机构沿半径为1.5 m的圆形轨迹运动。并联机构应用在数控机床和机器人等领域, 工作过程中通常处于匀速运动、加速运动和减速运动3种工作状态。因此, 运动过程也包括加速、匀速和减速3个阶段。另外, 为了比较冗余并联机构和非冗余并联机构的动力学性能, 仿真过程中, 去掉伸缩支链 $\begin{matrix} C_{4} D_{4}, \end{matrix}$ 得到对应的非冗余并联机构。让该非冗余并联机构也沿相同的圆形轨迹运动, 分别计算其驱动力和加速性能。

图3和图4给出了重型冗余并联机构和其对应的非冗余并联机构在仿真过程中的驱动力变化。可以看出在相同运动条件下非冗余并联机构最大驱动力明显高于冗余机构的最大驱动力, 非冗余并联机构的最小驱动力和冗余并联机构的最小驱动力差别不大。因此, 通过增加伸缩支链 $\begin{matrix} C_{4} D_{4}, \end{matrix}$ 可使并联机构的驱动力降低, 并且可以减小运动过程中驱动力波动, 从而提高机构的动态特性。

	Figure Option View Download New Window
	图3 冗余并联机构驱动力Fig.3 Driving force of redundant parallel mechanism

	Figure Option View Download New Window
	图4 非冗余并联机构驱动力Fig.4 Driving force of non-redundant parallel mechanism

3.2 冗余和非冗余并联机构加速度比较

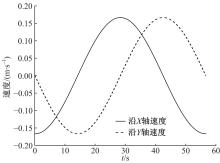
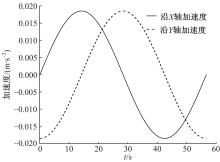
基于式(27)给出的加速度评价指标, 分别对冗余并联机构和其对应的非冗余并联机构在相同工作空间内的加速度性能进行仿真。图5和图6给出了并联机构沿半径为1.5 m的圆形轨迹运动时的速度和加速度, 可以看出在整个运动过程中 $\begin{matrix} X 、 Y \end{matrix}$ 方向的速度和加速度变化平缓。从图6中可以看出, 冗余并联机构和非冗余并联机构的加速度性能随着 $\begin{matrix} Y \end{matrix}$ 轴的变化较小。同时, 冗余并联机构的加速性能优于其对应的非冗余并联机构, 从而说明添加伸缩支链 $\begin{matrix} C_{4} D_{4} \end{matrix}$ 可以明显提升该并联机构的加速性能。

	Figure Option View Download New Window
	图5 动平台质心沿X、Y轴速度曲线Fig.5 Velocity curves of moving platform in X and Y axis

	Figure Option View Download New Window
	图6 动平台质心沿X、Y轴加速度曲线Fig.6 Acceleration curves of moving platform in X and Y axis

图7为冗余与非冗余机构的动力学性能对比, 可以看出该冗余并联机构的加速性能关于 $\begin{matrix} Y \end{matrix}$ 轴近似对称地, 并且在 $\begin{matrix} Y \end{matrix}$ 轴上的数值最大, 说明该并联机构在任务空间的中央具有最好的加速性能。考虑到在实际应用中, 该并联机构的任务空间也是在 $\begin{matrix} Y \end{matrix}$ 轴附近, 说明该并联机构在其任务空间中具有较高的工作效率, 为重载加工提供了一种非常实用的机构构型。

	Figure Option View Download New Window
	图7 冗余与非冗余机构的动力学性能对比Fig.7 Dynamic performances of redundant parallel mechanism and non-redundant parallel mechanism

4 结束语

本文提出了一种适合重载加工的2自由度龙门式驱动冗余并联机构, 该机构采用冗余驱动方式, 具有高刚度、低惯量等特点。利用虚功原理建立了系统的动力学模型, 并构造了并联机构加速性能评价指标。通过仿真研究表明, 在相同运动条件下, 冗余并联机构的驱动力小于对应的非冗余并联机构的驱动力, 从而降低了运动过程中驱动力的波动, 提高了动态特性。此外, 该冗余重型并联机构的加速性能优于其对应的非冗余并联机构的加速能力, 具有较高的工作效率。本文研究结果对其他重型并联机构的构型设计以及加速度评价具有重要的参考价值。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Ecorchard G, Neugebauer R, Maurine P. Elasto-geometrical modeling and calibration of redundantly actuated PKMs[J]. Mechanism and Machine Theory, 2010, 45(5): 795-810. [本文引用:1]
[2]	吴军, 李铁民, 关立文. 飞行模拟器运动平台的计算力矩控制[J]. 清华大学学报: 自然科学版, 2006, 46(8): 1405-1408. Wu Jun, Li Tie-min, Guan Li-wen. Computed-torque control for a moving flight simulator platform[J]. Journal of Tsinghua University(Science and Technology), 2006, 46(8): 1405-1408. [本文引用:1]
[3]	Hennes N. ECOSPEED—an innovative machinery concept for high performance 5-axis machining of large structural components in aircraft engineering[C]//Proceedings of 3rd Chemnitz Parallel Kinematics Seminar, Zwickau, Germany, 2002: 763-774. [本文引用:1]
[4]	Chung G J, Kim D H, Shin H. Structural analysis of 600 kg·f heavy duty hand ling robot[C]//IEEE International Conference on Robotics, Automation and Mechatronics, Anchorage, Alaska, USA, 2010: 40-45. [本文引用:1]
[5]	Bi Z M, Kang B. An inverse dynamic model of over-constrained parallel kinematic machine based on Newton-Euler formulation[J]. Journal of Dynamic Systems, Measurement, and Control, 2014, 136(4): 041001. [本文引用:1]
[6]	Asada H. A geometrical representation of manipulator dynamics and its application to arm design[J]. Journal of Dynamic Systems, Measurement, and Control, 1983, 105(3): 131-135. [本文引用:1]
[7]	Yoshikawa T. Dynamic manipulability of robot manipulators[J]. Journal of Robotic Systems, 1985, 2(1): 113-121. [本文引用:1]
[8]	Wu J, Gao Y, Zhang B, Wang L. Workspace and dynamic performance evaluation of the parallel manipulators in a spray-painting equipment[J]. Robotics and Computer Integrated Manufacturing, 2017, 44: 199-207. [本文引用:1]

2010

0.0

... 因此,并联机构得到了广泛的关注,出现了各种多自由度和少自由度并联机构构型,一些并联机构成功应用于飞行模拟器、数控机床、喷涂机器人等领域^[1,2] ...

2006

0.0

. 2006, 46(8):1405-1408

Computed-torque control for a moving flight simulator platform

飞行模拟器运动平台的计算力矩控制

Wu Jun , Li Tie-min , Guan Li-wen.

吴军, 李铁民, 关立文

2002

0.0

... 特别是Delta并联机器人、Z3并联机构主轴头的成功应用^[3],增强了研究人员对并联机构工业应用的信心 ...

2010

0.0

... 然而,适用于重型加工的并联机构构型相对较少,限制了并联机构的广泛应用和推广^[4] ...

2014

0.0

... 动力学是并联机构的重要性能,特别是并联机构应用于数控机床领域,对其动态特性要求更高^[5] ...

1983

0.0

... 目前,并联机构的动力学性能评价指标主要是沿用传统的串联机构动力学性能评价指标,还缺少驱动冗余并联机构的动力学性能评价方法及指标^[6,7] ...

1985

0.0

... 目前,并联机构的动力学性能评价指标主要是沿用传统的串联机构动力学性能评价指标,还缺少驱动冗余并联机构的动力学性能评价方法及指标^[6,7] ...

2017

0.0