超声波测距技术广泛地应用于各种工业测量与定位系统中, 如工业机器人的定位^[1]、AGV(Automated guided vehicle)小车的导航^[2]以及零部件装配生产线^[3]等。超声测距一般采用飞行时间法(Time of flight)^{[4, 5]}, 即通过超声波飞越时间与环境声速之积来解算飞行距离。环境声速可通过采集环境中的温度、湿度等信息求得^[6], 因此超声测距的精度一般取决于声波飞行时间能否精确提取。

超声信号一般由超声换能器产生, 换能器可将电信号与声信号进行相互转换, 回波信号在声电转换过程中很容易受到各种因素影响从而耦合入大量噪声^[7], 如测量环境的不稳定、电路耦合噪声以及被测物体表面粗糙度等, 这些噪声将极大地降低回波信号的信噪比, 使回波时间的提取产生较大的误差。

超声波信号耦合噪声的去除方法在大量文献中均有报道, 主要有设计滤波器法^[8]、频谱分离法^[9]、反馈神经网络法^[10]等, 但这些方法在应用过程中均存在一定的局限性, 即只能针对固定的噪声作时域上的分析, 无法对变化着的噪声作自适应性去除。超声信号一般为40 kHz以上的时变信号, 且其中耦合的噪声随着各种影响因素的变化将产生较大的变化, 因此在时域上对噪声进行滤除有着原理上的缺陷。小波分析算法是一种时域与频域结合的信号处理方法, 对于时域、频域兼有明显特征的声波信号处理有着独特优势^[11]。目前国内外学者们研究的小波去噪算法包括阈值法^[12]、小波包法^[13]、自适应滤波法^[14]等, 其中最常用的是阈值分析法, 即采用不同的阈值处理不同频率的小波分层信号, 最后再采用重构算法合成有用信号, 达到小波去噪的效果。传统的小波阈值法均采用固定的阈值与小波分层数^[15], 不能根据噪声信号的特征自动调整去噪阈值与分层数, 在噪声较高时去噪效果不明显, 而在噪声较低时则可能造成信号的失真, 并使系统运算量变大造成运算核心的资源浪费。

针对上述问题, 本文研究了一种自适应的小波去噪方法, 根据噪声水平与特征自动调整各层去噪阈值并获得最佳分层数, 提高系统运算效率, 有效地增加了信号信噪比, 使声波脉冲飞行时间的提取更加可靠、精确。最后, 搭建了测量精度比对实验平台, 验证了本文方法的精度与实用性。

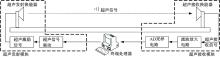
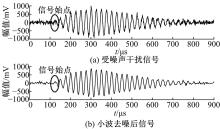
如图1所示, 超声测距系统一般由超声换能器发射与接收声波信号, 其中发射信号驱动电路调制后发射, 接收信号由滤波放大电路处理后经模数采样电路转化为数字信号由终端处理器处理。当被测距离较远时, 超声回波信号会受到较大地衰减, 因此需要放大电路对回波信号作放大处理, 在该信号被放大后, 环境与电路中引入的噪声也将被放大, 从而使信噪比下降, 淹没有效信号。典型的受噪声干扰的超声回波信号如图2所示。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 超声测距系统示意图Fig.1 Sketch map of a typical ultrasonic ranging system

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 含噪声的超声接收信号示意图Fig.2 Sketch map of noisy ultrasonic received signals

图2中超声接收信号显示, 该信号在信号起始点处受到了较大的干扰, 这使得通过信号起点提取声波飞行时间的方法产生了较大的误差。为了有效地增加超声接收信号的信噪比, 本文提出了一种基于自适应小波去噪的方法, 可有效剔除接收信号中的耦合噪声, 提升超声波距离测量的精度。

小波变换是一种十分有效的数字信号处理方法^[16], 相比于传统的傅里叶变换法只能对信号进行单纯的频域分析, 小波变换可以同时在时域和频域内对接收信号进行分解, 并从中提取出有效信号。

超声接收信号一般由有效信号与高斯白噪声耦合而成, 噪声信号一般频率较高, 而由其引发的小波分解系数模值相比于有效信号却比较小, 这样即可将耦合了噪声的接收信号作小波分层分解, 对各层小波分量作适当的阈值处理, 并将处理后的各层分量重新合成去噪后的信号, 实现通过小波分解去除信号噪声的目的。因此, 小波去噪的关键在于去噪阈值的优化与小波分层数的选择, 去噪阈值过大容易将有效信号消除, 使处理后的信号过分失真, 而小波分层数过少达不到良好的降噪效果, 过多又容易使运算量过大, 造成运算资源的浪费。为了更好地实现超声回波信号的去噪效果, 本文提出了一种自适应小波去噪方法, 可根据回波信号中噪声自动优化调整去噪阈值与小波分层数, 详述如下。

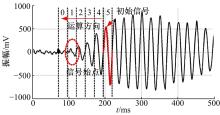
噪声信号一般分布在回波信号小波分解后频率较高的分量当中, 随着分解运算的不断进行, 频率较高的细节分量当中的噪声信号将逐渐降低, 而真实的超声接收信号能量则会逐渐变大, 这样就可以通过计算其中的高频分量与低频分量之间的相似性来确定是否还有必要继续进行小波分解。当它们之间的相关性系数比较小时, 说明高频细节分量中还存在着大量噪声, 需进一步对信号进行小波分解, 当相关性系数比较大时, 说明高频细节分量当中的噪声信号已比较小, 这时即可结束分解运算, 达到自动选择小波分解层数的目的, 优化运算资源。图3显示了对超声回波信号进行4层小波分解后的各层高频分量与低频分量, 以及各层相似性系数, 可见第3层相似性系数明显增大, 说明在层分解中的高频细节分量中已出现了较多的真实信号, 需对该层信号作尽可能地保留, 而第1层和第2层中则存在大量的噪声信号, 需采取有效的降噪措施, 而第4层在实际信号中则没有必要进行, 从而可以节约运算资源, 即最优分解层数为3层。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 超声接收信号4层小波分解示意图Fig.3 Sketch map of detail and approximate components decomposed for ultrasonic received signals

得到最优小波分解层数之后, 本文方法将采用实时提取信号中的噪声信号来确定合适的去噪阈值。由于高斯白噪声均匀地分布在整个接收信号当中, 因此可以通过在有效信号采集结束后继续对回波信号进行采样, 获得一段与接收信号同样长度的噪声, 对该噪声进行分析处理即可确定超声接收信号小波分解运算后的阈值大小, 从而得到良好的降噪效果。传统的阈值选取方法一般采用统一阈值法, 该阈值与噪声的标准差及噪声采样长度有关, 当采样点较多时, 该阈值会将小波高频细节分量都置零, 使降噪后的信号过于失真, 达不到较好的降噪效果。由于超声回波信号中的噪声一般服从正态分布, 而正态分布中根据 3σ原理, 信号幅值超过 3σ的概率非常小^[17], 这样就可将 3σ以内的信号看作噪声信号, 而将超过 3σ的值处理为有效信号, 且超声测距原理是要提取超声波脉冲的飞行时间, 这样就有必要保留超声接收信号起始处的微弱信号, 因此, 为了避免起振处幅度较小的有效信号被阈值处理掉, 实际应用中可采用较小的阈值, 如 2σ,而对含有较多有效信号的高频分量, 其去噪阈值可用 0.2σ或直接保留, 从而达到良好的去噪效果。

通过采样噪声信号评估出合适的小波降噪阈值后, 即可通过阈值处理函数对超声回波信号进行去噪处理, 小波降噪函数一般可采用硬阈值函数和软阈值函数, 其中硬阈值函数由于在阈值点处不连续, 会在信号奇异点附近产生信号畸变现象, 故本文方法采用软阈值函数对接收到的超声回波信号进行处理, 并将降噪处理后的高频分量与低频分量重构, 实现回波信号的去噪, 去噪后的信号如图4所示。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 受噪声干扰与小波去噪后的超声接收信号Fig.4 Noisy and de-noisy ultrasonic received signals

传统的超声测距方法中飞行时间的提取一般采用固定阈值法^[18], 这样由于接收信号强弱的变化, 容易造成所提取的飞行时间产生整周期性的偏差, 从而造成较大的测量误差。为避免这种情况, 本文提出了一种采用自相关性运算的方法来提取超声飞行时间。自相关算法即对接收信号自身作相关性运算, 从而自动识别接收回波信号的信号起始位置, 而与信号的强弱无关, 在保证飞行时间提取精度的前提下提高了算法的稳定性。

连续信号 x(t)在 t1时刻与 t1+τ时刻的自相关函数 Rx(τ)可通过式(1)求得:

Rx(τ)=limT→∞1/T∫0Tx(t)x(t+τ)dt1

对于周期函数 x(t),其自相关函数 Rx(τ)也为周期函数, 且当 τ为周期的整数倍时, 自相关函数可以取最大值。那么对于超声接收函数而言, 任意两个周期的自相关函数必然接近于1。为了提高自相关算法的有效法, 本文算法一般取回波信号的峰值附近的一个周期信号作为初始比对信号; 然后计算初始信号与回波信号中该初始信号之前的各个周期信号的自相关系数。对于自相关系数接近1的信号可认为是有效的超声回波信号, 而当出现自相关系数显著降低的信号, 则可认为是噪声信号, 这样就可有效地提取超声回波信号的起始位置, 进而精确得出超声脉冲的飞行时间。本文算法示意图如图5所示。

图5

Fig.5

	Figure Option ViewDownloadNew Window
	图5 基于自相关法的超声接收信号始点提取算法示意图Fig.5 Sketch map of onset extraction method for ultrasonic received signals by using self-correlation method

为验证本文小波降噪算法的有效性与超声测距的精度, 设计了以下两个实验对其进行验证。首先是超声回波信号的去噪效果验证, 然后通过精密导轨作距离基准验证超声测距的测量精确度。如图6所示, 验证实验平台由安装在精密导轨上的超声传感器对组成, 超声收发模块采用SensComp公司的600系列传感器, 其中心频率为50 kHz, 发射器发射超声信号由数字频率合成器电路产生的调制信号激发, 接收信号首先由模数转换器将模拟信号转换为数字信号, 再由终端处理器处理后在显示终端显示最终的测试与分析结果。实验过程中, 超声发射器固定不动, 而超声接收器可沿精密导轨移动, 测量过程从1000 mm开始到3000 mm为止, 每隔100 mm移动一次。当接收器接收到超声信号后, 首先对信号进行小波降噪处理, 然后通过本文自相关法提取声波的飞行时间, 而环境声速可通过式(2)估算, 最终通过飞行时间法解算得到被测距离。

c(t)=331.091+t273.152

式中: t为环境温度, 由精密温度计测得。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 验证平台示意图Fig.6 Sketch map of verification experiment platform

首先, 将对小波降噪算法的有效性进行验证。在接收信号中随机抽取5组进行分析验证, 接收信号将分别采用传统的固定阈值法与本文自适应阈值法进行噪声去除, 为了量化处理结果, 本文通过计算信号的信噪比来表征信号中的噪声大小, 信噪比越大, 说明噪声含量越少, 信噪比计算公式如下:

SNR=10lg∑si2∑si-sni23

式中: si为理想的超声波接收信号, 可由Matlab程序模拟生成; sni为含噪声的超声接收信号, 降噪效果如表1所示。

表1

Table 1

表1(Table 1)

表1 不同方法小波去噪效果 Table 1 De-nosing results with different methods 序号 SNR0 SNR1 SNR2 Δ SNR1 Δ SNR2 1 13.1 16.2 20.2 3.1 7.1 2 12.8 15.4 18.6 2.6 5.8 3 13.9 16.4 19.8 2.5 5.9 4 13.5 16.7 19.8 3.2 6.3 5 12.9 15.8 19 2.9 6.1

表1 不同方法小波去噪效果 Table 1 De-nosing results with different methods

其中, SNR₀为超声接收信号信噪比; SNR₁、SNR₂分别为通过传统方法与本文去噪方法得到的信噪比; Δ SNR₁、Δ SNR₂分别为采用传统方法与本文方法处理后的信号信噪比增量。可见本文方法信噪比增量相比普通方法提高了约3 dB, 且有较高的稳定性。

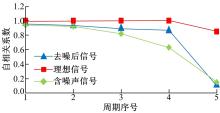
其次, 为了验证去噪信号采用本文的自相关法提取超声接收信号的起始点的有效性, 实验中采用一组信号计算其初始信号之前各周期的自相关系数, 并分别对理想信号、含噪声的超声接收信号以及小波降噪后的信号作同样的处理, 其自相关系数如图7所示。

图7

Fig.7

	Figure Option ViewDownloadNew Window
	图7 自相关算法结果示意图Fig.7 Sketch map of results for self-correlation algorithm

从图7可看出, 理想信号与去噪后信号的自相关系数在初始信号前第5个超声周期均出现了明显下降, 而含噪声的信号则第4个周期已经出现了明显下降, 这样就很容易造成超声接收信号起始点的误判, 产生整周期的测量误差。因此, 本文小波降噪方法具有较好的稳定性, 有效地提高了信号起始点的识别度。

最后, 对采用本文超声测距方法的测量精度进行验证。由前述实验条件可知, 测量范围为1000~3000 mm, 超声接收器接收到超声波信号后, 通过不同方法提取声波脉冲飞行时间以及环境声速, 得到被测距离, 测量结果如图8所示。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 超声测距精度结果示意图Fig.8 Sketch map of results for ultrasonic ranging experiments

实验结果表明, 采用传统的固定阈值法, 其测量结果不太稳定, 与精密导轨给定的基准距离相比, 其最大测量误差达到1.3 mm, 而采用本文的自适应小波去噪法, 测量误差可控制在0.28 mm以内, 且稳定性较高。

本文提出了一种基于自适应小波去噪法的精密超声波测距方法, 通过小波去噪算法提高超声接收信号的信噪比, 使接收信号起始点附近的有用信号锐度提升, 提高飞行时间的提取精度。自适应小波去噪方法通过实时采集接收信号中的噪声信号作为去噪基准, 为有效信号的小波去噪提供合适的去噪阈值, 使之能够自动适应不同信噪比的信号。然后, 通过对小波分解得到的不同层数之间的高频细节分量与低频近似分量作相关性运算, 确定出最优分层数, 优化系统的运算效率。最后, 通过小波重构算法得到去噪后的信号, 并采用自相关算法提取超声接收信号的起始点, 得到精确地超声脉冲飞行时间, 有效地提高了超声测距的测量精度。实验表明, 接收信号的信噪比得到了显著提升, 与精密导轨提供的基准距离相比, 在3000 mm的实测距离范围内, 其误差小于0.28 mm, 该测距精度可满足大部分工业制造领域中距离测量的要求。