新型摆线针轮行星减速器传动系统的振动特性

引用本文

陈忠敏, 侯力, 段阳, 张祺, 杨忠学, 蒋易强. 新型摆线针轮行星减速器传动系统的振动特性[J].吉林大学学报（工学版）, 2018,48(1): 174-185
CHEN Zhong-min, HOU Li, DUAN Yang, ZHANG Qi, YANG Zhong-xue, JIANG Yi-qiang. Vibration analysis of a new pin-cycloid speed reducer[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(1): 174-185 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20161139
Permissions

新型摆线针轮行星减速器传动系统的振动特性

陈忠敏^1,², 侯力¹, 段阳¹, 张祺³, 杨忠学², 蒋易强¹

1. 四川大学制造科学与工程学院,成都 610065

2. 四川建安工业有限责任公司技术中心,四川雅安 625000

3. 攀枝花学院机械工程学院,四川攀枝花 617000

作者简介:陈忠敏(1988-),男,博士研究生.研究方向:新型传动技术. E-mail:zhongmin_chen@126.com

基金:国家自然科学基金项目(51375320); 攀枝花市应用技术研究与开发项目(2016CY-G-10)

摘要

为减少刚性摆线针轮行星减速器工作时的振动,提高运行可靠性,设计了一种带减振衬垫的非刚性摆线针轮行星减速器,并对其进行非线性振动分析。综合考虑了时变刚度、轴向误差、啮入冲击等激励,基于集中参数理论和牛顿第二定律建立新型摆线针轮行星减速器8自由度的多因素耦合动力学模型和振动微分方程组,采用变步长四阶Runge-Kutta法对量纲归一化后的方程组进行求解。对比了刚性与非刚性结构下的摆线轮、低速轴的垂直振动和扭转振动情况,结果表明:采用减振衬垫,使摆线轮和低速轴的垂直振动和扭转振动效应都降低。进一步对新型摆线针轮行星减速器进行实验测试分析,结果表明:实验所测数据结果与其振动情况的理论分析结果较吻合。

关键词: 机械设计; 新型摆线针轮行星减速器; 减振衬垫; 非线性振动; 动态设计

中图分类号:TH132.4 文献标志码:A 文章编号:1671-5497(2018)01-0174-12

Vibration analysis of a new pin-cycloid speed reducer

CHEN Zhong-min^1,², HOU Li¹, DUAN Yang¹, ZHANG Qi³, YANG Zhong-xue², JIANG Yi-qiang¹

1. School of Manufacturing Science and Engineering, Sichuan University, Chengdu 610065, China

2. Jian'an Industrial Co., Ltd., Technology Center, Ya'an 625000, China

3. School of Mechanical Engineering, Panzhihua University, Panzhihua 617000, China

Abstract

In order to reduce the vibration of rigid pin-cycloid speed reducer and improve its operational reliability, a non-rigid pin-cycloid speed reducer with damping mat is designed its nonlinear vibration characteristics are analyzed. Taking into consideration of three internal excitations, including time-varying stiffness, axial error and meshing impact, an eight-degrees of freedom multi-factor coupling dynamic model of the designed pin-cycloid speed reducer is established based on the theory of concentrated parameter, and the vibration differential equations are set up based on Newton second law. Then, the equations are solved by adopting the fourth-order Runge-Kutta algorithm with variable step length. The verticality and the torsion vibration characteristics of the cycloid gear and low speed shaft of the new pin-cycloid speed reducer are compared with that of traditional one. Results show that the verticality and the torsion vibration of the cycloid gear and low speed shaft are reduced by the damping mat. Also the theoretical analysis is verified by measurement data from the test of the new reducer.

Keyword: mechanical design; new pin-cycloid speed reducer; damping mat; non-linear vibration characteristic; dynamic design

Show Figures

0 引言

摆线针轮行星减速器具有传动比变换范围大、体积小、传动精度高等特点, 常用于替代两级、三级传动的普通圆柱齿轮减速器和圆柱蜗杆减速器。伴随机器人、精密机械传动、高新技术设备等行业需求的不断提高, 摆线针轮行星减速器的工作性能必将在苛刻的振动、噪声和可靠性等技术标准要求下进一步提升。由于摆线针轮行星减速器的振动效应直接反映传动系统的性能与工作可靠性, 所以国内外学者对摆线针轮行星减速器的研究已从基础静力学向弹性动力学深入。Chen等^[1]依据齿轮啮合基本原理, 推导出少齿差行星传动的啮合方程、啮合副的共轭齿廓方程和接触线方程等, 并分析摆线轮与针齿的共轭啮合特性, 提出采用包络法形成摆线轨迹的思路。Xu等^[2]提出一种可精确预估摆线针齿动态啮合对数、确定接触点位置并获取接触载荷的动力学分析方法。Li^[3]运用弹性接触理论研究参数变化下的行星减速器运行中的接触问题。Hsieh^[4]研究摆线轮修形量对摆线针轮行星减速器动态性能的影响。Song等^[5]通过数值仿真和实验研究摆线针轮减速器的传动特点以及针轮动态性能。李俊阳等^[6]通过变形协调设计出渐开线少齿差行星传动, 利用仿真与实验研究其空程回差、润滑及动力学特性的改善情况。Sun等^[7]研究摆线针轮行星减速器的针轮驱动情况以及应力的分布区域, 给出修正后的针轮接触应力的计算方法。孙章栋等^[8]研究摆线针轮传动的接触热弹流润滑特性, 得到摆线针轮副完整啮合周期内摩擦力及摩擦损失功率变动。杨冰等^[9]分析并测试摆线针轮行星减速器工作的振动和噪声。何卫东^[10]通过改变环板式针摆行星传动的结构, 以及对主、从齿的齿廓进行优化修缘来降低其振动, 并进行了实验研究。

上述摆线针轮行星减速器的振动研究, 在建模和分析中都忽略一些非线性因素, 研究不够深入, 有些工作缺乏试验和工程数据。再结合现有摆线针轮行星减速器使用现状, 由于转矩和转速的波动、各零部件的制造误差和装配误差、零部件的磨损等, 导致摆线针轮行星减速器的传动精度降低、传动振动和噪声迅速上升, 甚至出现卡死的现象。因此, 针对现有摆线针轮行星减速器存在的一些技术不足和研究忽略的影响因素, 提出一种安装减振衬垫的新型摆线针轮行星减速器, 并综合考虑啮合副间的非线性因素影响, 对新设计的摆线针轮行星减速器的振动进行研究, 为后续摆线针轮行星减速器的动态设计、降噪提供理论依据和技术支持。

1 新型摆线针轮行星减速器传动原理

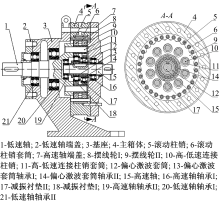
新型摆线针轮行星减速器主要结构部件:偏心驱动输入机构(部件7、12~16、19)、减振件(部件17和18)、摆线针轮啮合机构(部件3~6、8和9)和输出传动机构(部件1、2、10、11、20和21), 结构原理图如图1所示。

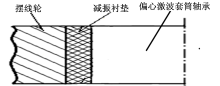
	Figure Option View Download New Window
	图1 新型摆线针轮行星减速器结构原理图Fig.1 Structure schematic diagram of new pin-cycloid speed reducer

减振件是新型摆线针轮行星减速器减振降噪的关键传动件, 图2示出了减振衬垫的安装位置, 主要用于减小、阻断电机和传动过程中产生的高频波动, 并向低频段转移, 提高传动精度。

	Figure Option View Download New Window
	图2 减振衬垫安装位置示意图Fig.2 Installation diagram of damping mat

传动原理:偏心激波套筒、偏心激波套筒轴承I和II相对于高速轴偏心安装; 偏心激波套筒轴承I和II运动相位相差180° ; 偏心激波套筒轴承I和II外圈分别装有减振衬垫Ⅰ 和Ⅱ ; 在减振衬垫I和II外圈上装有相位相差180° 的摆线外齿轮I和Ⅱ 。高速轴转动, 带动偏心激波套筒、偏心激波套筒轴承I和II转动, 带动摆线外齿轮I和II以高速轴轴线为中心做公转运动。摆线外齿轮Ⅰ 和Ⅱ 的外齿廓与滚动柱销套筒相啮合, 滚动柱销套筒的轴线由滚动柱销所固定, 故滚动柱销套筒会对摆线外齿轮I和II产生与其公转方向相反的力, 推动摆线外齿轮Ⅰ 和Ⅱ 相对于高速轴以摆线外齿轮I和II的轴线为中心进行反向自转, 且推动高-低速连接柱销套筒及高-低速链接柱销以低速轴为中心相对于高速轴反向转动, 继而带动低速轴相对于高速轴做反向转动, 从而达到减速增矩的目的。

2 系统内部激励

摆线轮传动系统的动态激励是产生噪声和振动的根本原因, 文中仅研究摆线轮与滚动柱销套筒、摆线轮柱销孔与高-低速连接柱销套筒间啮合时的内部激励, 包括时变刚度、制造安装误差以及啮入冲击激励。

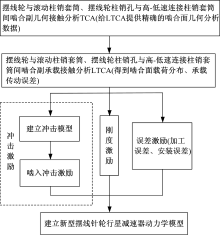
图3为摆线轮传动系统内部激励计算流程图, 利用摆线轮与滚动柱销套筒、摆线轮柱销孔与高-低速连接柱销套筒啮合副啮合接触分析的结果, 可准确进行内部激励的计算。相关几何接触分析和承载接触分析以及摆线轮与滚动柱销套筒、摆线轮柱销孔与高-低速连接柱销套筒啮合副啮合接触分析见啮合分析文献所述计算方法^{[3, 4, 5, 11, 12, 13]}。

	Figure Option View Download New Window
	图3 内部激励计算流程图Fig.3 Calculation flow chart of internal excitations

2.1 计算时变刚度激励

要精确建立摆线轮与滚动柱销套筒、摆线轮柱销孔与高-低速连接柱销套筒的啮合刚度模型比较困难, 文中采用分解摆线轮运动过程来模拟摆线轮的整个运动过程, 利用摆线轮与滚动柱销套筒、摆线轮柱销孔与高-低速连接柱销套筒啮合副承载接触分析得到不同啮合位置的接触力和接触变形, 从而得到该位置的啮合刚度。摆线针轮行星减速器传动比为29, 故高速轴转动一周, 摆线轮旋转约12.4° 。在整个啮合过程中, 若某啮合位置有多对摆线轮参与啮合, 那么该啮合位置的啮合综合刚度是由在该位置同时参与啮合的单对啮合刚度叠加而成, 将啮合刚度的离散值通过多项式拟合和Fourier 级数变换展开成周期函数。

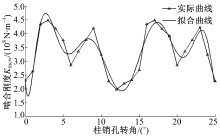
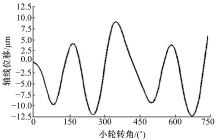
图4为摆线轮与滚动柱销套筒啮合副两个啮合周期内的啮合刚度变化趋势和拟合曲线, 综合刚度值以约12° 为周期变化, 与理论计算周期12.4° 基本一致。刚度最大值为2.4× 10⁸N/m, 最小值为1.28× 10⁸ N/m, 差值接近1倍。图5为摆线轮柱销孔与高-低速连接柱销套筒啮合副两个啮合周期内的啮合刚度变化趋势和拟合曲线, 综合刚度值周期也与计算周期12.4° 接近, 最大值为1.74× 10⁸ N/m, 最小值为0.48× 10⁸ N/m, 差值约2.5倍。由于啮合区域随啮入或啮出呈现周期性变化, 故综合刚度的最大值和最小值相差较大, 且具有周期性, 是系统产生振动和噪声的一个重要因素。

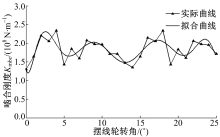	Figure Option View Download New Window
	图4 摆线轮与滚动柱销套筒啮合综合刚度曲线图Fig.4 Synthetical meshing stiffness curve of cycloid gear with rolling pin-sleeve

	Figure Option View Download New Window
	图5 柱销孔与高-低速连接柱销套筒啮合综合刚度曲线图Fig.5 Synthetical meshing stiffness curve of cylindrical pin hole with high-low speed connection pin-sleeve

2.2 计算传动误差激励

研究中仅考虑摆线轮齿形误差和基节误差, 根据摆线轮加工精度等级通过查手册, 合成系统等效误差, 再通过简谐函数来模拟误差。低转速下, 摆线轮制造安装误差引起的轴向位移也是摆线轮高速运动时振动的激励源。根据摆线轮齿形误差和基节误差, 利用摆线轮副承载接触分析得到低转速下长周期内的轴向位移, 经Fourier 级数展开后其周期函数曲线见图6。

	Figure Option View Download New Window
	图6 轴向位移曲线Fig.6 Axial displacement

2.3 计算冲击激励

啮合冲击主要是由啮入、啮出和节点冲击组成, 三者对于摆线轮传动性能的影响, 啮入冲击最大, 故本文仅考虑啮入冲击对系统的影响。最大啮入冲击力计算公式^[14]:

F_s=Δ v $\begin{matrix} \sqrt[]{\frac{b J_{1} J_{2}}{(J_{1} r_{b 2}^{2} + J_{2} r_{b 1}^{2}) q_{s}}} \end{matrix}$ (1)

式中:Δ v是啮入冲击速度; J₁、J₂对应啮合物体1和2的转动惯量; r_b1、r_b2对应啮合物体1和2的瞬时啮合线对应的瞬时基圆半径; b是摆线轮宽; q_s是初始啮入点处的综合柔度。

将得到的啮合点的冲击力通过多项式拟合以及Fourier级数变换展开成周期函数。转速1400 r/min时, 一个啮合周期内摆线轮与滚动柱销套筒、摆线轮柱销孔与高-低速连接柱销套筒的啮入冲击力曲线见图7。

	Figure Option View Download New Window
	图7 啮入冲击力曲线图Fig.7 Meshing impact

3 空间动力学模型

在实际工程中, 摆线针轮行星减速器系统的传动是非常复杂的, 故基于以下假设建立振动模型:不考虑摆线针轮行星减速器传动系统中各旋转、滑动、啮合接触等部位的摩擦力影响; 用等效弹簧刚度表示传动系统中回转副、啮合副和支持轴承处所产生的弹性变形; 减振衬垫I和II的物理和几何参数一致, 摆线轮I和II的物理和几何参数一致。

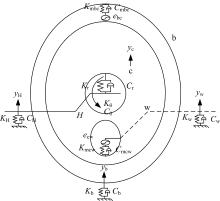
应用集中参数法建立新型摆线针轮行星减速器系统的非线性振动模型, 图8是简化后的振动模型, 建立的振动系统包含8个自由度:

{δ }={y_H, θ _H, y_b, θ _b, y_c, θ _c, y_w, θ _w}(2)

式中:y_i、θ _i表示高速轴H、滚动柱销套筒b、摆线轮c、低速轴w的垂直振动位移和扭转振动位移, i=H, b, c, w。

	Figure Option View Download New Window
	图8 传动系统的非线性振动模型Fig.8 Nonlinear vibration model of transmission system

需将减振衬垫的影响考虑到系统内部各部件的振动微分方程中, 得到垂直和扭转方向的振动微分方程:

$\begin{matrix} \{\begin{matrix} m_{H} {\ddot{y}}_{H} + C_{H} {\dot{y}}_{H} + K_{H} f_{H} (y_{H}) - C_{r} ({\dot{y}}_{H} - {\dot{y}}_{c}) - \\ K_{r} (y_{H} - y_{c}) = 0 \\ I_{H} {\ddot{θ}}_{H} + C_{θ} {\dot{θ}}_{H} - C_{a} {\dot{θ}}_{c} + K_{θ} θ_{H} - K_{a} θ_{c} = T_{H} \end{matrix} \end{matrix}$

(3)

$\begin{matrix} \{\begin{matrix} m_{b} {\ddot{y}}_{b} + C_{b} {\dot{y}}_{b} + K_{b} f_{b} (y_{b}) - C_{mbc} (Δ {\dot{y}}_{bc} + {\dot{y}}_{b} - \\ {\dot{y}}_{c} - {\overset{\cdot}{e}}_{bc}) - K_{mbc} (t) f_{mbc} (Δ y_{bc} + y_{b} - \\ y_{c} - e_{bc}) = 0 \\ I_{b} {\ddot{θ}}_{b} + C_{mbc} (Δ {\dot{y}}_{bc} + {\dot{y}}_{b} - {\dot{y}}_{c} - {\dot{e}}_{bc}) r_{p} + \\ K_{mbc} (t) f_{mbc} (Δ y_{bc} + y_{b} - y_{c} - e_{bc}) r_{p} = T_{H} \end{matrix} \end{matrix}$ (4)

$\begin{matrix} \{\begin{matrix} m_{c} {\ddot{y}}_{c} + C_{r} ({\dot{y}}_{H} - {\dot{y}}_{c}) + K_{r} (y_{H} - y_{c}) + \\ C_{mbc} (Δ {\dot{y}}_{bc} + {\dot{y}}_{b} - {\dot{y}}_{c} - {\dot{e}}_{bc}) + K_{mbc} (t) \times \\ f_{mbc} (Δ y_{bc} + y_{b} - y_{c} - e_{bc}) - C_{mcw} (Δ {\dot{y}}_{cw} + \\ {\dot{y}}_{c} - {\dot{y}}_{w} - {\dot{e}}_{cw}) - K_{mcw} (t) (Δ y_{cw} + y_{c} - \\ y_{w} - e_{cw}) = 0 \\ I_{c} {\ddot{θ}}_{c} - C_{θ} {\dot{θ}}_{H} + C_{a} {\dot{θ}}_{c} - K_{θ} θ_{H} + K_{a} θ_{c} - \\ C_{mbc} (Δ {\dot{y}}_{bc} + {\dot{y}}_{b} - {\dot{y}}_{c} - {\dot{e}}_{bc}) r_{c} - \\ K_{mbc} (t) (Δ y_{bc} + y_{b} - y_{c} - e_{bc}) r_{c} + \\ C_{mcw} (Δ {\dot{y}}_{cw} + {\dot{y}}_{c} - {\dot{y}}_{w} - {\dot{e}}_{cw}) R_{w} + \\ K_{mcw} (t) (Δ y_{cw} + y_{c} - y_{w} - e_{cw}) R_{w} = 0 \end{matrix} \end{matrix}$ (5)

$\begin{matrix} \{\begin{matrix} m_{w} {\ddot{y}}_{w} + C_{w} {\dot{y}}_{w} + K_{w} f_{w} (y_{w}) + C_{mcw} (Δ {\dot{y}}_{cw} + \\ {\dot{y}}_{c} - {\dot{y}}_{w} - {\dot{e}}_{cw}) + K_{mcw} (t) (Δ y_{cw} + y_{c} - \\ y_{w} - e_{cw}) = 0 \\ I_{w} {\ddot{θ}}_{w} - C_{mcw} (Δ {\dot{y}}_{cw} + {\dot{y}}_{c} - {\dot{y}}_{w} - {\dot{e}}_{cw}) R_{w} - \\ K_{mcw} (t) (Δ y_{cw} + y_{c} - y_{w} - e_{cw}) R_{w} = - T_{w} \end{matrix} \end{matrix}$ (6)

式中:m_i、I_i分别为高速轴H、滚动柱销套筒b、摆线轮c、低速轴w的质量和转动惯量, i=H, b, c, w; C_i、K_i分别为支撑等效元件模型的阻尼和刚度, i=H, b, w; C_θ、K_θ分别为高速轴扭转阻尼和扭转刚度; C_r、K_r分别为减振衬垫径向阻尼和刚度; C_a、K_a分别为减振衬垫扭转阻尼和刚度; C_mbc、K_mbc分别为摆线轮与滚动柱销套筒啮合阻尼和时变啮合刚度; C_mcw、K_mcw分别为摆线轮柱销孔与高-低速连接柱销套筒啮合阻尼和时变啮合刚度; f_i(y_i)为间隙型非线性力-位移函数, i=H, b, w; T_H、T_w为输入转矩和输出转矩; r_c为摆线轮分度圆半径; R_w为柱销孔中心圆半径; r_p为滚动柱销中心圆半径; e_bc、e_cw为静态传递误差; Δ y_bc、Δ y_cw为动态传递误差。

啮合线上的相对位移:

$\begin{matrix} \{\begin{matrix} Δ y_{bc} = r_{p} θ_{b} - r_{c} θ_{c} \\ Δ y_{cw} = r_{c} θ_{c} - r_{w} θ_{w} \end{matrix} \end{matrix}$ (7)

各啮合副法向阻尼均由下式求得:

c=2ζ _v $\begin{matrix} \sqrt[]{Km} \end{matrix}$ (8)

式中:ζ _v为各啮合副对应的相对啮合阻尼系数, 计算中取0.065; K为各啮合副对应的平均啮合刚度; m为各啮合副对应的等效质量。

当y_i> 3b_i(振动间隙), 间隙型非线性力-位移函数的非线性程度并不明显, 近似转化为分段线性函数:

f_i(y_i)= $\begin{matrix} \{\begin{matrix} y_{i} - b_{i}, y_{i} > b_{i} \\ 0, - b_{i} \leq y_{i} \leq b_{i} \\ y_{i} + b_{i}, y_{i} < - b_{i} \end{matrix} \end{matrix}$ (9)

4 动力学模型的求解与分析

表1为新型摆线针轮行星减速器的等效机构参数, 利用仿真摆线轮与滚动柱销套筒、摆线轮柱销孔与高-低速连接柱销套筒啮合特性的结果, 得到上述啮合综合刚度图4和图5, 以及低转速下摆线轮的轴向位移图6和啮合冲击激励图7。采用变步长四阶Runge-Kutta对降阶后的振动微分方程组求解, 对比刚性与非刚性结构下的摆线轮、低速轴的垂直振动和扭转振动。

表1 等效机构参数 Table 1 Equivalent mechanism parameters

4.1 垂直振动对比

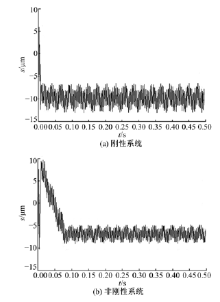
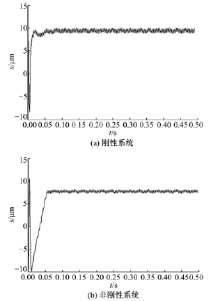
图9为传动系统达到工作稳态时摆线轮的垂直振动位移。图9(a)中振动平衡点位置维持在-10 μ m, 且在0.01 s后趋于稳定, 幅值约为2.8 μ m。图9(b)中振动平衡时间约0.07 s, 振动平衡点位置维持在-7 μ m, 幅值约1.5 μ m。非刚性系统下的摆线轮的平衡振动位移值比刚性振动模型的对应值降低约3 μ m, 振动幅值减小。

	Figure Option View Download New Window
	图9 摆线轮垂直振动位移Fig.9 Vertical vibration displacement of cycloid gear

图10为低速轴垂直振动位移。图10(a)低速轴经小幅振动后达到振动平衡时间约为0.05 s, 平衡点位置在9.2 μ m, 振动幅值约为0.6 μ m。图10(b)振动平衡时间约为0.06 s, 振动平衡点位置在7.5 μ m, 振动幅值约为0.5 μ m。非刚性系统下的低速轴的平衡点振动位移值比刚性振动模型的对应值降低约1.7 μ m, 振动幅值降低约0.3 μ m 。图9、图10的结果表明, 在新型摆线针轮行星减速器中添加减振衬垫后, 摆线轮和低速轴的垂直振动平衡点位移值和振动幅值都减小, 在垂直方向起到减振的效果。

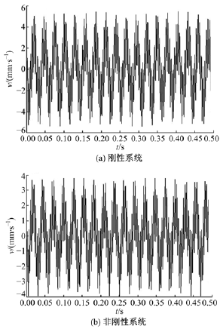
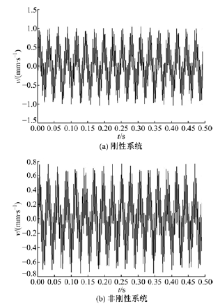
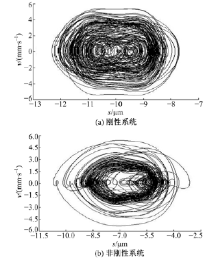
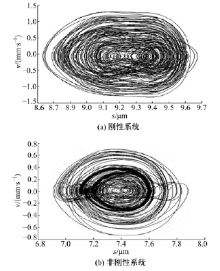
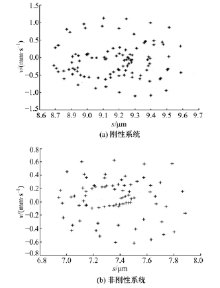
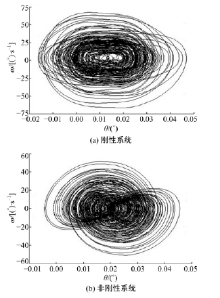
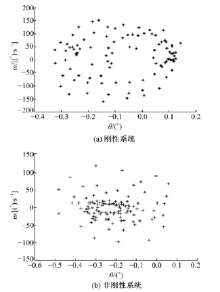
	Figure Option View Download New Window
	图10 低速轴垂直振动位移Fig.10 Vertical vibration displacement of low speed shaft

图11为传动系统达到工作稳态时摆线轮的垂直振动速度。图11(a)中速度振动幅值约为5.8 mm/s, 图11(b)中速度振动幅值约为4 mm/s。图12为稳态时低速轴的垂直振动速度, 图12(a)中幅值约为1 mm/s, 图12(b)中幅值约为0.8 mm/s。图11、图12数据表明, 新型减速器的摆线轮和低速轴的振动速度幅值均比刚性减速器的对应值小, 减振衬垫使垂直方向的振动程度降低。图13和图14是刚性与非刚性结构下的摆线轮和低速轴的垂直振动位移-速度相图, 二者相图为近似环形闭合曲面和不规则椭圆闭合曲面相互往复重叠由内向外交叉循环扩展, 表明摆线轮和低速轴呈现稳态响应的近混沌状态。此外, 相图中表明非刚性结构下的摆线轮和低速轴的垂直振动位移-速度相图曲线比刚性情况的更具有规律性。图15和图16是对应图13和图14的摆线轮和低速轴垂直振动位移-速度Poincaré 截面, 图中显示各个截面均为成片分布的密集点, 且每个点都可以在各自相图曲线上一一对应。密集点存在一定方向性, 但Poincaré 截面的规律性并不强, 说明刚性与非刚性结构下的摆线针轮和低速轴处于稳态响应的近混沌状态, 与各相图分析结果一致。

	Figure Option View Download New Window
	图11 摆线轮垂直振动速度Fig.11 Vertical vibration velocity of cycloid gear

	Figure Option View Download New Window
	图12 低速轴垂直振动速度Fig.12 Vertical vibration velocity of low speed shaft

	Figure Option View Download New Window
	图13 摆线轮垂直振动位移-速度相图Fig.13 Vertical vibration displacement-velocity phase of cycloid gear

	Figure Option View Download New Window
	图14 低速轴垂直振动位移-速度相图Fig.14 Vertical vibration displacement-velocity phase of low speed shaft

	Figure Option View Download New Window
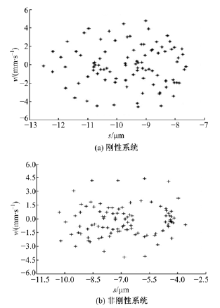	图15 摆线轮垂直振动位移& 速度Poincaré 截面Fig.15 Vertical vibration displacement-velocity Poincaré section of cycloid gear

	Figure Option View Download New Window
	图16 低速轴垂直振动位移-速度Poincaré 截面Fig.16 Vertical vibration displacement-velocity Poincaré section of low speed shaft

4.2 扭转振动对比

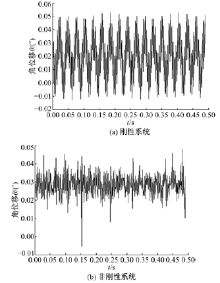
图17为传动系统工作稳态时摆线轮的扭转振动角位移。图17(a)中振动平衡点位置维持在0.02° , 幅值约0.03° 。图17(b)中平衡点位置维持在0.028° , 振动幅值约0.013° 。对比两种情况下的摆线轮扭转振动, 都很快达到振动平衡, 图17(b)中振动平衡点偏离角值比图17(a)的对应值将近大0.01° , 但振动幅值要小0.017° 。说明新型摆线针轮行星减速器中添加减振衬垫后, 由于减振衬垫的变形导致摆线轮的扭转振动平衡点位置变大, 同时对内部的振动起到缓冲, 使振动幅值减小。

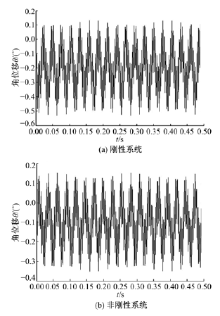
	Figure Option View Download New Window
	图17 摆线轮扭转振动角位移Fig.17 Torsional vibration angular of cycloid gear

图18为传动系统工作稳态时低速轴的扭转振动角位移。图18(a)中低速轴振动平衡点位置维持在-0.2° , 幅值约0.3° 。图18(b)中振动平衡点位置维持在-0.1° , 振动幅值约0.23° 。对比两种情况下的低速轴扭转振动, 都很快达到振动平衡, 图18(b)中低速轴的振动平衡点偏离角值比图18(a)中的值小0.1° , 振动幅值减小约0.07° 。说明新型摆线针轮行星减速器中添加减振衬垫后, 使低速轴的振动角位移和振动幅值都减小。

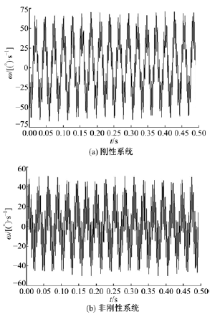
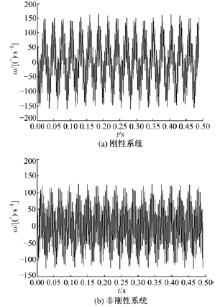
	Figure Option View Download New Window
	图18 低速轴扭转振动角位移Fig.18 Torsional vibration angular of low speed shaft

图19为传统系统工作稳态时摆线轮的扭转振动角速度, 图19(a)中振动幅值约为70 ° /s, 图19(b)中振动幅值约为50 ° /s。图20为工作稳态时低速轴的扭转振动角速度, 20(a)中振动幅值约为150 ° /s, 20(b)中振动幅值约为120 ° /s。图19和图20的数据表明, 新型减速器的摆线轮和低速轴振动角速度的幅值小于刚性结构下的对应值, 说明减振衬垫在摆线轮和低速轴扭转方向起到减振作用。

	Figure Option View Download New Window
	图19 摆线轮扭转振动角速度Fig.19 Torsional vibration angular velocity of cycloid gear

	Figure Option View Download New Window
	图20 低速轴扭转振动角速度Fig.20 Torsional angular velocity of low speed shaft

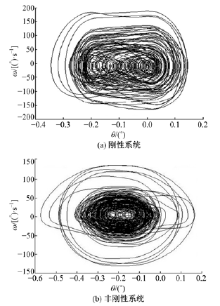
图21和图22是刚性与非刚性结构下的摆线轮和低速轴的扭转振动角位移-角速度相图, 表明摆线轮和低速轴呈现稳态响应的近混沌状态, 这一点与前述垂直振动情况相同。图23和图24是对应图21和图22的摆线轮和低速轴扭转振动角位移-角速度Poincaré 截面, 图中显示各个截面均为成片分布的密集点, 且每个点都可以在各自相图曲线上一一对应。密集点存在一定方向性, 但Poincaré 截面的规律性并不强, 说明刚性与非刚性结构下的摆线针轮和低速轴处于稳态响应的近混沌状态, 与各相图分析结果一致。对比垂直振动和扭转振动的相图与Poincaré 截面, 扭转振动的规律性比垂直振动情况好。

	Figure Option View Download New Window
	图21 摆线轮扭转振动角位移-角速度相图Fig.21 Torsional vibration angular-angular velocity phase of cycloid gear

	Figure Option View Download New Window
	图22 低速轴扭转振动角位移-角速度相图Fig.22 Torsional vibration angular-angular velocity phase of low speed shaft

	Figure Option View Download New Window
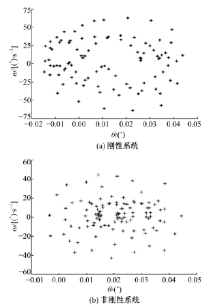	图23 摆线轮扭转振动角位移-角速度Poincaré 截面Fig.23 Torsional vibration angular-angular velocity Poincaré section of cycloid gear

	Figure Option View Download New Window
	图24 低速轴扭转振动角位移-角速度Poincaré 截面Fig.24 Torsional vibration angular-angular velocity Poincaré section of low speed shaft

5 振动测试

依据《GB8543-1987》对新型摆线针轮行星减速器的摆线轮和低速轴二者的表面进行振动测试, 采用加速度传感器获取加速度振动信号, 通过信号采集处理分析仪对采集的数据进行记录和分析处理。

实验主要设备:INV3020C型高精度信号采集处理仪、INV9832 ICP三向加速度传感器、INV1841电荷调理仪等设备以及DASP V10数据采集与信号处理软件。实验中主要分析新型摆线针轮行星减速器的摆线轮和低速轴的垂直方向振动, 并与传统摆线针轮行星减速器的相关测试值进行比较, 传感器布置点如图25所示。

	Figure Option View Download New Window
	图25 传感器布置Fig.25 Sensor sites

表2为输入转速分别为500、1000、1500 r/min三种工况下测试点处振动加速度的测试值, 实验中对每处测试点的振动加速度测取3次后求平均值, 作为测试值。

结果表明:理论研究中的3种不同转速工况下摆线轮垂直振动加速度峰值频率分别出现在826.2、1392.4 和1832.7 Hz, 与实验测得的摆线轮垂直振动加速度值出现的峰值频率821.4、1382.3和1824.5 Hz比较接近; 不同转速下低速轴垂直振动加速度峰值频率分别出现在51.3、114.6和162.5 Hz, 与实验测得的低速轴垂直振动加速度值出现的峰值频率46.6、107.4和153.4 Hz也比较接近。同时可以看到, 摆线轮垂直振动加速度峰值0.8527、1.4622和1.9337 m/s²也接近实验测得的峰值0.8251、1.2236和1.6854 m/s²; 低速轴垂直振动加速度峰值0.2566、0.3725和0.6113 m/s²与实验测得的峰值0.2225、0.3426和0.5817 m/s²也比较接近。此外, 与传统摆线针轮行星减速器对应工况下的摆线轮垂直振动加速度测试值0.7833、1.0832和1.5894 m/s², 以及对应的低速轴垂直振动加速度测试值0.2055、0.2988和0.4727 m/s²相比较, 二者的测试值和幅值均降低。以上动力学分析表明:新型摆线针轮行星减速器的振动理论分析结果与实验所测数据结果比较吻合, 达到了预期研究目标。

表2 实验测试值 Table 2 Test data

6 结论

(1)以降低刚性摆线针轮行星减速器工作时的振动和提高其可靠性为主要研究目标, 提出了一种安装减振衬垫的新型摆线针轮行星减速器, 并基于集中参数理论和牛顿第二定律建立其8自由度的多因素耦合动力学方程, 对刚性与非刚性结构下的摆线轮和低速轴的垂直振动和扭转振动进行仿真与实验比较分析。

(2)基于文中建立的振动模型进行仿真实验, 仿真数据表明:采用减振衬垫, 摆线轮和低速轴的垂直振动和扭转振动变化更加平稳, 为后续动态设计提供了理论依据。

(3)完成新型摆线针轮行星减速器样机实验测试, 实验结果与文中理论分析结果符合较好, 验证了新型摆线针轮行星减速器工作时的振动特性比刚性结构的系统要好, 说明文中提出的安装减振衬垫具有可行性, 为其减振降噪提供了一种结构设计方案。

(4)研究中忽略了摩擦、回转零件的偏心质量、箱体的变形等因素, 在后续建立更加精确的动力学模型中应考虑这些参数的影响。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Chen Bing-kui, Fang Ting-ting, Li Chao-yang. Gear geometry of cycloid drives[J]. Science in China Series E: Technological Sciences, 2008, 51(5): 598-610. [本文引用:1]
[2]	Xu Li-xin, Yang Yu-hu. Dynamic modeling and contact analysis of a cycloid-pin gear mechanism with a turning arm cylindrical roller bearing[J]. Mechanism and Machine Theory, 2016, 104: 327-349. [本文引用:1]
[3]	Li S. Design and strength analysis methods of the trochoidal gear reducers[J]. Mechanism and Machine Theory, 2014, 81: 140-154. [本文引用:2]
[4]	Hsieh Chiu Fan. Traditional versus improved designs for cycloidal speed reducers with a small tooth difference: the effect on dynamics[J]. Mechanism and Machine Theory, 2015, 86: 15-35. [本文引用:2]
[5]	Song Yuan, Liao Qi-zheng. Modelling, simulation and experiment of a novel pure rolling cycloid reducer with involute teeth[J]. International Journal of Modelling, Identification and Control, 2014, 21(2): 184-192. [本文引用:2]
[6]	李俊阳, 王家序. 渐开线少齿差行星传动的变形协调设计[J]. 中国机械工程, 2014, 25(5): 576-580. Li Jun-yang, Wang Jia-xu. Deformation and compatibility design of involute planetary gear drive with small teeth difference[J]. China Mechanical Engineering, 2014, 25(5): 576-580. [本文引用:1]
[7]	Sun Ying-shi, Guan Tian-min, Zhang Xu. Dynamic simulation of cycloid wheel at two support points of needle gear pin for new three-gear pin-cycloid driven speed reducer[J]. Advanced Materials Research, 2011, 291: 1195-1199. [本文引用:1]
[8]	孙章栋, 朱才朝, 刘怀举. 摆线针轮传动接触热弹流润滑特性[J]. 振动与冲击, 2016, 35(6): 174-180. Sun Zhang-dong, Zhu Cai-chao, Liu Huai-ju. TEHL characteristics of a cycloid drive[J]. Journal of Vibration and Shock, 2016, 35(6): 174-180. [本文引用:1]
[9]	杨冰, 刘岩. 双曲柄四环板式针摆行星减速器减振降噪研究[J]. 兵工学报, 2011, 32(10): 1282-1286. Yang Bing, Liu Yan. Vibration and noise reduction of a double crank four ring-plate-type cycloid speed reducer[J]. Acta Armamentarii, 2011, 32(10): 1282-1286. [本文引用:1]
[10]	何卫东. 双曲柄环板式针摆行星传动降低振动与噪声的优化设计与试验[J]. 机械工程学报, 2010, 46(23): 53-60. He Wei-dong. Optimum design and experiment for reducing vibration and noise of double crank ring-plate-type pin-cycloid planetary drive[J]. Journal of Mechanical Engineering, 2010, 46(23): 53-60. [本文引用:1]
[11]	Blagojevic M, Marjanovic N, Djordjevic Z. Numerical and experimental analysis of the cycloid disc stress state[J]. Tehnicki Vjesnik, 2014, 21(2): 377-382. [本文引用:1]
[12]	Litvin F L. Design simulation of meshing, and contact stress for an improved worm gear drive[J]. Mechanism and Machine Theory, 2007, 42: 940-959. [本文引用:1]
[13]	刘志峰, 张志民. 基于多项式的等高齿锥齿轮时变啮合刚度建模[J]. 吉林大学学报: 工学版, 2013, 43(4): 939-944. Liu Zhi-feng, Zhang Zhi-min. Modelling of high-spiral bevel gear mesh stiffness based on polynomial[J]. Journal of Jilin University (Engineering and Technology Edition), 2013, 43(4): 939-944. [本文引用:1]
[14]	周长江, 唐进元. 齿轮传动的线外啮合与冲击摩擦[J]. 机械工程学报, 2008, 44(3): 75-81. Zhou Chang-jiang, Tang Jin-yuan. Corner contact and impact friction of gear drive[J]. Journal of Mechanical Engineering, 2008, 44(3): 75-81. [本文引用:1]

2008

0.0

... Chen等^[1]依据齿轮啮合基本原理,推导出少齿差行星传动的啮合方程、啮合副的共轭齿廓方程和接触线方程等,并分析摆线轮与针齿的共轭啮合特性,提出采用包络法形成摆线轨迹的思路 ...

2016

0.0

... Xu等^[2]提出一种可精确预估摆线针齿动态啮合对数、确定接触点位置并获取接触载荷的动力学分析方法 ...

2014

0.0

... Li^[3]运用弹性接触理论研究参数变化下的行星减速器运行中的接触问题 ...

... 相关几何接触分析和承载接触分析以及摆线轮与滚动柱销套筒、摆线轮柱销孔与高-低速连接柱销套筒啮合副啮合接触分析见啮合分析文献所述计算方法^{[3,4,5, 11,12,13]} ...

2015

0.0

... Hsieh^[4]研究摆线轮修形量对摆线针轮行星减速器动态性能的影响 ...

2014

0.0

... Song等^[5]通过数值仿真和实验研究摆线针轮减速器的传动特点以及针轮动态性能 ...

2014

0.0

. 2014, 25(5):576-580 DOI:doi:10.3969/j.issn.1004-132X.2014.05.002

Deformation and compatibility design of involute planetary gear drive with small teeth difference

渐开线少齿差行星传动的变形协调设计

Li Jun-yang , Wang Jia-xu.

李俊阳, 王家序

Aiming at involute planetary gear drive with small teeth difference, a design method of deformation and compatibility was proposed, including design of composite gear with multilayer material, material selection and structure design of the elastic layer, and the design formulas for center distance of gear with backlash-free where the deformation of elastic material was considered. On the basis of this method, a filter transmission device was designed and manufactured. The comparative analyses and experiments with the normal planetary transmission driver which had the same structure and specifications was also conducted. The results suggest that filtering gear driver's backlash, lubrication and kinetic characteristics are improved obviously.

针对渐开线少齿差行星传动，提出了一种变形协调设计方法，包括多层材料复合的齿轮本体设计、弹性层的材料选择及结构设计、考虑弹性材料变形的齿轮无侧隙啮合中心距设计计算公式。在此基础上设计制造了一种滤波传动装置，并与相同结构形式及规格的普通行星减速器进行了传动性能的对比仿真分析与实验，结果表明滤波减速器的空程回差、润滑及动力学特性都有了较为明显的改善。

... 李俊阳等^[6]通过变形协调设计出渐开线少齿差行星传动,利用仿真与实验研究其空程回差、润滑及动力学特性的改善情况 ...

2011

0.0

... Sun等^[7]研究摆线针轮行星减速器的针轮驱动情况以及应力的分布区域,给出修正后的针轮接触应力的计算方法 ...

2016

0.0

. 2016, 35(6):174-180

TEHL characteristics of a cycloid drive

摆线针轮传动接触热弹流润滑特性

Sun Zhang-dong , Zhu Cai-chao , Liu Huai-ju.

孙章栋, 朱才朝, 刘怀举

... 孙章栋等^[8]研究摆线针轮传动的接触热弹流润滑特性,得到摆线针轮副完整啮合周期内摩擦力及摩擦损失功率变动 ...

2011

0.0

. 2011, 32(10):1282-1286

Vibration and noise reduction of a double crank four ring-plate-type cycloid speed reducer

双曲柄四环板式针摆行星减速器减振降噪研究

Yang Bing , Liu Yan.

杨冰, 刘岩

... 杨冰等^[9]分析并测试摆线针轮行星减速器工作的振动和噪声 ...

2010

0.0

. 2010, 46(23):53-60 DOI:doi:10.3901/JME.2010.23.053

Optimum design and experiment for reducing vibration and noise of double crank ring-plate-type pin-cycloid planetary drive

双曲柄环板式针摆行星传动降低振动与噪声的优化设计与试验

He Wei-dong.

何卫东

双曲柄环板式针摆行星传动是一种高承载能力和高传动效率的新型传动装置.它有多种结构型式,从中选择两种主要结构型式,以提高承载能力为目标进行优化设计,研制出样机进行性能试验,它们都具有高的承载能力和高的传动效率.介绍这两种能传递更大功率且动态特性更优的主要结构型式和进一步提高其动态特性的研究成果.其中,以提高承载能力为目标进行优化设计的三齿轮联动双曲柄四环板针摆行星传动的样机,高转速满负荷工作时的噪声为92 dB;而振动的评级为好.经过以降低振动和噪声为目标的改进优化设计后,高转速满负荷工作时的噪声为85 dB,噪声降低了7 dB,其评级指标也上升为"好";同时样机的振动性能又得到进一步的改善.

... 何卫东^[10]通过改变环板式针摆行星传动的结构,以及对主、从齿的齿廓进行优化修缘来降低其振动,并进行了实验研究 ...

2014

0.0

2007

0.0

2013

0.0

. 2013, 43(4):939-944

Modelling of high-spiral bevel gear mesh stiffness based on polynomial

基于多项式的等高齿锥齿轮时变啮合刚度建模

Liu Zhi-feng , Zhang Zhi-min.

刘志峰, 张志民

2008

0.0

. 2008, 44(3):75-81

Corner contact and impact friction of gear drive

齿轮传动的线外啮合与冲击摩擦

Zhou Chang-jiang , Tang Jin-yuan.

周长江, 唐进元

... 最大啮入冲击力计算公式^[14]: ...