未知环境下智能汽车轨迹规划滚动窗口优化

引用本文

张琳, 章新杰, 郭孔辉, 王超, 刘洋, 刘涛. 未知环境下智能汽车轨迹规划滚动窗口优化[J].吉林大学学报（工学版）, 2018,48(3): 652-660
ZHANG Lin, ZHANG Xin-jie, GUO Kong-hui, WANG Chao, LIU Yang, LIU Tao. Rolling window optimization for intelligent vehicle trajectory planning in unknown environment[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 652-660 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170323
Permissions

未知环境下智能汽车轨迹规划滚动窗口优化

张琳¹, 章新杰¹, 郭孔辉¹, 王超¹, 刘洋², 刘涛³

1.吉林大学汽车仿真与控制国家重点实验室,长春 130022

2.长春孔辉汽车科技股份有限公司, 长春130012

3. 中国第一汽车集团公司技术中心,长春 130011

通讯作者：章新杰(1984-),男,副教授,博士.研究方向:车辆动力学及控制,驾驶员模型,智能汽车.E-mail:zhangxinjie5885@163.com

作者简介:张琳(1991-),男,博士研究生.研究方向:车辆动力学及控制,智能汽车.E-mail:zhanglin_jlu@foxmail.com

基金:国家自然科学基金项目(51675217,51705186); 国家自然科学基金联合基金项目(U1564213); 江西科技学院产业升级协同创新中心开放基金项目(16XTKFYB02); 中国科协青年人才托举工程项目(2016QNRC001).

摘要

为解决多约束条件下智能汽车在未知环境中生成全局最优轨迹的问题,引入滚动窗口优化策略,在研究车辆动力学模型特性的基础上,提出了一种能够同时满足行驶安全和全局最优的动态轨迹规划方法。为保证车辆在行驶过程中轨迹连续平稳,采用六次多项式生成曲率连续的轨迹,并将轨迹规划问题转化为求解单个多项式系数的过程。考虑车辆自身约束以及环境约束对轨迹生成速度的影响,对规划窗口中的障碍物按照度量函数进行分类,并根据最优指标决策出当前规划窗口下的局部最优轨迹和车速。利用Simulink-CarSim搭建了环境模型以及轨迹规划模型,最后通过仿真试验验证了该方法的有效性。

关键词: 车辆工程; 智能汽车; 轨迹规划; 车辆动力学; 滚动窗口

中图分类号:U469.7 文献标志码:A 文章编号:1671-5497(2018)03-0652-09

Rolling window optimization for intelligent vehicle trajectory planning in unknown environment

ZHANG Lin¹, ZHANG Xin-jie¹, GUO Kong-hui¹, WANG Chao¹, LIU Yang², LIU Tao³

1.State Key Laboratory of Automotive Simulation and Control, Jilin University, Changchun 130022,China

2.KH Automotive Technologies (Changchun) Co.Ltd., Changchun 130012,China

3.R&D Center,China Faw Group Corporation, Changchun 130011,China;

Abstract

In order to solve the trajectory planning of intelligent vehicle with multi-constraint conditions in unknown environment, a rolling optimization scheme is presented. A feasible trajectory planning method in the local environment is proposed via vehicle dynamic study. With the characteristics of smooth trajectories of six polynomials, the process of trajectory planning is transformed into solving a single polynomial coefficient. The obstacles in the planning window are classified according to the metric function, and the optimal trajectory and vehicle speed are decided according to the optima index. Simulink and CarSim are used to develop the environmental model and the trajectory model. The effectiveness of the planning scheme is verified by simulation study.

Keyword: vehicle engineering; intelligent vehicles; trajectory planning; vehicle dynamics; rolling window

文章图片

0 引言

轨迹规划是实现汽车智能化的关键技术之一, 其主要任务是在有障碍物的行驶环境中找到一条从初始点到目标点的安全轨迹, 并满足所有约束条件。智能汽车的轨迹规划问题具有如下特点:①不确定性:行车过程中, 车辆只能通过传感器或车载雷达在有限的探测区域中获取局部信息, 在探测未知环境时, 障碍物的突然出现会增加轨迹规划的难度。②多约束:智能汽车的轨迹规划不仅要考虑车辆运动存在的几何约束, 还需要考虑非完整性约束以及车辆的动力学约束对轨迹规划的影响。除此之外, 道路边界、交通规则以及驾驶员的驾驶习惯等也对轨迹规划提出了更高的要求^[1]。

针对多约束条件下智能汽车在未知环境中的轨迹规划问题, 传统方法是将应用在机器人领域的轨迹规划算法用于生成车辆轨迹, 例如人工势场法、模拟退火算法等^{[2, 3, 4]}, 这类方法具有结构简单、计算量较小的优点, 但算法难以处理动态变化的驾驶环境且容易陷入局部最优解, 限制了轨迹规划在智能汽车中的应用。为克服传统方法的缺点, 文献[5, 6]提出了基于学习和人工智能理论的规划方法, 例如神经网络, 遗传算法等, 车辆在行进中能够不断融合、分析探测到的信息, 逐步建立起全局环境模型并进行一定程度的全局优化, 但是这种方法信息冗余较多、计算量大, 在实际应用中不能满足实时性的要求。文献[7, 8, 9]对上述方法进行了改进, 如A^*, D^*等, 这类方法通过一个估价函数来估计当前点到终点的距离, 并由此决定搜索方向, 可以根据车辆在移动中探测到的环境信息快速修正和规划出最优路径, 具有一定的复杂环境自适应能力, 但是没有考虑车辆非完整约束的限制, 影响了智能汽车的轨迹跟踪效果。文献[10, 11]提出的快速搜索随机树(Rapidly exploring random tree, RRT), 采用树结构解决复杂约束下的轨迹规划问题, 由于搜索速度快且适用于包含运动学和动力学约束的规划, 使得该算法在机器人领域得到了广泛应用。但是RRT采用随机采样策略, 导致生成的轨迹重复性不强, 算法的随机性还会导致生成的轨迹出现明显的拐角或者绕远, 无法被车辆直接执行。

为解决智能汽车在未知环境中生成全局最优轨迹的问题, 本文提出了一种基于滚动窗口优化的轨迹规划方法。该方法在建立车辆模型和环境模型的基础上, 通过6次多项式生成平滑轨迹, 利用滚动窗口周期性地刷新窗口内的环境信息, 并根据车辆当前状态对轨迹进行在线优化。最后仿真验证了本文算法的有效性。

1 问题描述及分析

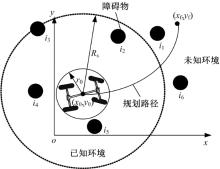
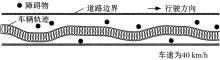
汽车的工作环境如图1所示, 在二维平面中 $(x_{0}, y_{0}) 、 (x_{f}, y_{f})$ 分别为车辆的起点位置和目标位置; $i_{1}, i_{2}, \dots, i_{n}$ 为分布在车辆周围的静态障碍物; $R_{s}$ 为车辆行驶过程中的探测半径; $R_{s}$ 范围内的环境为探测到的已知环境, $R_{s}$ 范围外的环境为未知环境。为了简化计算, 采用圆形对行驶车辆及障碍物进行包络。因此, 可以将全局环境未知情况下的轨迹规划问题定义为:已知车辆起始位姿、目标运动位姿以及探测到的环境信息, 根据所给定的地图规划出一条满足各项约束的最优行驶轨迹。

	Figure Option View Download New Window
	图1 智能汽车工作环境描述Fig.1 Intelligent vehicle working environment description

1.1 路径表示

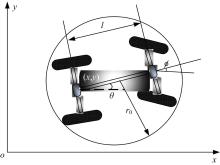
为了便于描述, 建立了车辆运动学模型, 如图2所示, 模型可表示为:

$(\begin{array}{l} \overset{\cdot}{x} \\ \overset{\cdot}{y} \\ \overset{\cdot}{θ} \\ \overset{\cdot}{ϕ} \end{array}) = (\begin{array}{l} \cos (θ) & 0 \\ \sin (θ) & 0 \\ \frac{1}{l} \tan (θ) & 0 \\ 0 & 1 \end{array}) (\begin{array}{l} u_{1} \\ u_{2} \end{array}) (1)$

	Figure Option View Download New Window
	图2 车辆运动学模型Fig.2 Vehicle kinematic model

式中: $(x, y)$ 为车辆后轴中点坐标; $ϕ$ 为前轮转角; $θ$ 为车身方向角; $l$ 为前后轴距; $u_{1}$ 为车速; $u_{2}$ 为前轮转角速度。

由式(1)可进一步获取状态量之间的关系表达式:

$\frac{\partial y}{\partial x} = \tan θ; \frac{\partial^{2} y}{\partial x^{2}} = \frac{\tan ϕ}{l \cos θ} (2)$

结合式(1)(2), 并选取 $(x, y, θ, ϕ)$ 为车辆的位姿信息, 求解路径曲线的边界条件可表示为:

$\begin{array}{l} \{\begin{array}{l} (x_{0}, y_{0}) (x_{0}, θ_{0}) (x_{0}, ϕ_{0}) \\ (x_{f}, y_{f}) (x_{f}, θ_{f}) (x_{f}, ϕ_{f}) \end{array} \Leftrightarrow \\ \{\begin{array}{l} (x_{0}, y_{0}) (x_{0}, {\partial y / \partial x|}_{x_{0}}) (x_{0}, {\partial^{2} y / \partial x^{2}|}_{x_{0}}) \\ (x_{f}, y_{f}) (x_{f}, {\partial y / \partial x|}_{x_{f}}) (x_{f}, {\partial^{2} y / \partial x^{2}|}_{x_{f}}) \end{array} (3) \end{array}$

式中:x₀、x_f分别为惯性坐标系下路径起始点和目标点的横坐标值。

考虑车辆在轨迹过程中的平稳性以及参数的求解效率, 采用具有连续曲率的多项式轨迹模型, 将路径曲线表示为路径上任一点的纵坐标 $y$ 关于横坐标 $x$ 的六次多项式函数:

$\begin{array}{l} y = a_{0} + a_{1} x + a_{2} x^{2} + a_{3} x^{3} + \\ a_{4} x^{4} + a_{5} x^{5} + a_{6} x^{6} (4) \\ x_{0} \leq x \leq x_{f} \end{array}$

式中: $a = [a_{0}, a_{1}, \dots, a_{6}]$ 为路径曲线参数向量。

在每一时刻, 若以车辆当前位置为初始位置进行轨迹规划, 联立式(1)~(4)可解得 $a_{0} ~ a_{5},$ 其表达式为:

$\begin{array}{l} [a_{0} a_{1} a_{2} a_{3} a_{4} a_{5}]^{T} = \\ (B^{k})^{- 1} (Y^{k} - A^{k} a_{6}) (5) \\ Y^{k} = {[\overset{\cdot}{y} |_{x = x_{k}}, \overset{\cdot \cdot}{y} |_{x = x_{k}}, \overset{\cdot}{y} |_{x = x_{f}}, \overset{\cdot \cdot}{y} |_{x = x_{f}}]}^{T} (6) \\ A^{k} = [x_{k}^{6}, 6 x_{k}^{5}, 30 x_{k}^{4}, x_{f}^{6}, 6 x_{f}^{5}, 30 x_{f}^{4}]^{T} (7) \\ B^{k} = [\begin{array}{l} 1 & x_{k} & x_{k}^{2} & x_{k}^{3} & x_{k}^{4} & x_{k}^{5} \\ 0 & 1 & 2 x_{k} & 3 x_{k}^{2} & 4 x_{k}^{3} & 5 x_{k}^{4} \\ 0 & 0 & 2 & 6 x_{k} & 12 x_{k}^{2} & 20 x_{k}^{3} \\ 1 & x_{f} & x_{f}^{2} & x_{f}^{3} & x_{f}^{4} & x_{f}^{5} \\ 0 & 1 & 2 x_{f} & 3 x_{f}^{2} & 4 x_{f}^{3} & 5 x_{f}^{4} \\ 0 & 0 & 2 & 6 x_{f} & 12 x_{f}^{2} & 20 x_{f}^{3} \end{array}] (8) \end{array}$

式中: $x_{k}$ 为车辆当前位置的横坐标值, 初始状态下 $x_{k} = x_{0} 。$

规划出的路径是以 $a_{6}$ 为变量的多项式曲线, 设 $a_{6}^{k}$ 为当前时刻的 $a_{6}$ 值, 则规划出的路径曲线表达式为:

$\begin{array}{l} y = [1 x x^{2} x^{3} x^{4} x^{5} x^{6}] \\ (B^{k})^{- 1} (Y^{k} - A^{k} a_{6}^{k}) + a_{6}^{k} x^{6} (9) \end{array}$

由式(5)~式(9)可知:在已知车辆初始位姿和目标位姿时, 轨迹规划问题可转化为求解 $a_{6}^{k}$ 的过程。

1.2 轨迹规划的约束条件

汽车轨迹规划的两类最重要的约束为路径可行性约束和安全性约束^[12], 可具体分为几何约束和运动学约束、道路边界约束以及车辆动力学约束。

1.2.1 几何约束和运动学约束

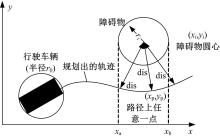
为保证车辆安全行驶, 在行驶过程中需要与障碍物之间有一定的安全避障距离, 以静态障碍物为研究对象, 避障约束示意图如图3所示。

	Figure Option View Download New Window
	图3 避障约束示意图Fig.3 Schematic of obstacle constraint

图3中, 分别用半径为 $r_{i} 、 r_{0}$ 的圆包裹行驶车辆和障碍物。 $(x_{i}, y_{i})$ 为包裹障碍物圆的圆心坐标; $X_{a} 、 X_{b}$ 分别为障碍物左边界和右边界横坐标; $(x_{p}, y_{p})$ 为路径上任意一点坐标; $dis$ 为 $(x_{i}, y_{i})$ 到 $(x_{p}, y_{p})$ 的距离, 若要使车辆避开障碍物, dis需满足式(10):

$\begin{array}{l} dis \geq (r_{i} + r_{0}) \Rightarrow \\ (y_{p} - y_{i})^{2} + (x_{p} - x_{i})^{2} \geq (r_{i} + r_{0})^{2} (10) \\ X_{a} \leq x_{p} \leq X_{b} \end{array}$

联立式(9)(10)可得到利用多项式描述路径的避障约束数学表达式:

$\begin{array}{l} \min H_{i} (a_{6}^{k}) = \min_{x \in [x_{k}, x_{f}]} h_{2} (x) (a_{6}^{k})^{2} + \\ h_{1, j} (x) (a_{6}^{k}) + h_{0, i} (x) \geq 0 (11) \end{array}$

式中:

$\begin{array}{l} h_{0, i} (x) = [g (x) (B^{k})^{- 1} Y^{k} - y_{i}]^{2} + \\ (x - x_{i})^{2} - (r_{i} + r_{0})^{2}; \\ h_{1, i} (x) = 2 [x^{6} - g (x) (B^{k})^{- 1} A^{k}] \times \\ [g (x) (B^{k})^{- 1} Y^{k} + y_{i}]^{2}; \\ h_{2} (x) = [x^{6} - g (x) (B^{k})^{- 1} A^{k}]; \end{array}$

$g (x) = [1 x x^{2} x^{3} x^{4} x^{5}] 。$

通过式(11)可进一步求解出 $a_{6}^{k}$ 在避障约束下的数学表达式为:

$\Omega^{k} = \bigcap\limits_{^{i \in {1, 2, …, n}}} [- \infty, a^{k}_{6 si}] \cup [a^{k}_{6 si}, +\infty] \quad (12)$

式中: $Ω^{k}$ 为满足避障约束 $a_{6}^{k}$ 的集合; $n$ 为检测到的障碍物的个数; $a_{6 si}^{k} 、 a_{6 bi}^{k}$ 分别为:

$\{\begin{array}{l} a_{6 si}^{k} = (- h_{1, i} - \sqrt{(h_{1, i})^{2} - 4 h_{2} h_{0, i}}) / 2 h_{2} \\ a_{6 bi}^{k} = (- h_{1, i} + \sqrt{(h_{1, i})^{2} - 4 h_{2} h_{0, i}}) / 2 h_{2} \end{array} (13)$

1.2.2 道路边界约束

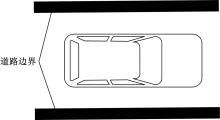
在真实的行车环境中, 需要对道路边界进行识别并考虑道路边界对轨迹规划的影响。为了减小计算量, 假设道路边界为矩形, 将道路边界也视为一种障碍物, 即保证车辆在行驶过程中不触碰到道路边界。用直径为矩形最小边长的圆对道路边界进行包络, 并且将道路边界视为障碍物, 因此道路边界约束被化简为几何约束。对道路边界的处理如图4所示。

	Figure Option View Download New Window
	图4 道路边界处理Fig 4 Road boundary processing

1.2.3 车辆动力学约束

智能汽车控制系统是一个受非完整性约束的非线性系统, 因此车辆轨迹规划在满足避障约束的同时还要满足动力学约束要求。当车速一定时, 行驶轨迹曲率与侧向加速度成正比, 车辆在实际运动过程中产生的侧向加速度受到发动机、轮胎、地面附着系数等多方面限制, 同时为了保证行驶过程中驾驶员乘坐的舒适性, 需要对最大侧向加速度进行约束, 侧向加速度约束如下所示:

$| \overset{\cdot \cdot}{y} | \leq a_{y \max} (14)$

式中:a_y_max为最大侧向加速度, m/s²。

受车辆转向系统限制, 其前轮转向角变化范围有限且变化过程连续进行, 由于任意时刻后轴中心点处的线速度始终垂直于后轴, 因此转向角约束可以被转换成几何约束来处理, 由几何关系易得:

$\tan ϕ = l / R (15)$

式中: $R 为转弯半径; l$ 为前、后轴距。

因此, 最大转向角约束以及转向角连续约束可以转化为对转弯半径的约束, 其数学表达式为:

$\begin{array}{l} κ_{\max} = 1 / R_{\min} = \tan ϕ_{\max} / l (16) \\ κ = \frac{\overset{\cdot \cdot}{y}}{[1 + {(\overset{\cdot}{y})]}^{3 / 2}} \leq κ_{\max} (17) \end{array}$

式中: $κ$ 为轨迹曲率; R_min为最小转弯半径; κ _max为最大曲率; ϕ _max为最大转向角。

1.3 目标函数

本文以路径最短作为性能指标, 因此选取距离函数作为目标函数, 通过求解目标函数在约束条件中的极值来确定点集的运动方程, 最终使迭代路径点集趋于最优规划路径^[13]:

$\begin{array}{l} \min {J^{L}}_{k} (a_{6}^{k}) = \int_{x_{k}}^{x_{f}} |y - \frac{y_{f} - y_{k}}{x_{f} - x_{k}} (x - x_{k}) - y_{0}| d x \\ s.t. \{\begin{array}{l} \min H_{i} (a_{6}^{k}) \geq 0 \\ \overset{\cdot \cdot}{y} \leq a_{y \max} \\ k \leq k_{\max} \end{array} (18) \end{array}$

式中: $(x_{k}, y_{k})$ 为车辆当前位置的坐标。

由于车辆位姿在行驶过程中时刻改变, 由式(18)易知, 车辆需要根据车辆当前状态和周围环境的状态信息, 考虑多个约束规划出可行的参考路径, 综上述, 轨迹规划的过程是随着车辆运动求取 $a_{6}^{k}$ 的动态规划过程^[14]。

2 基于滚动窗口优化的轨迹规划算法

当环境信息已知时, 离线的全局轨迹规划可以使智能汽车在有障碍物的工作环境中寻找一条从给定起点到终点的可行路径, 使其在运动过程中能安全、无碰撞地绕过所有障碍物。然而, 在许多情况下车辆只能探测到局部环境信息, 本文提出了一种的基于滚动窗口优化的轨迹规划算法。

2.1 滚动窗口优化原理

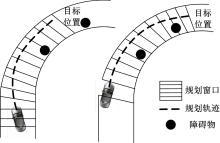
障碍物未知环境中, 移动车辆只能通过传感器获取到静态的局部环境信息, 充分利用这些信息便可以实现一个局部环境的轨迹规划, 若干个这样的局部规划前后衔接就可以完成一项全局轨迹规划任务, 其原理如图5所示。

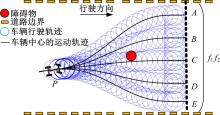
	Figure Option View Download New Window
	图5 滚动窗口原理Fig.5 Rolling window principle

将传感器可以探测到的区域定义为视觉窗口, 车辆当前位置到目标位置的区域定义为规划窗口, 如图5所示。规划窗口在每一步长下都向车辆行驶方向滚动, 在滚动的每一步, 根据探测到的局部信息, 用启发式方法生成优化子目标, 在当前滚动窗口内进行局部轨迹规划, 随着滚动窗口的推进, 不断取得新的环境信息, 从而在滚动中实现优化与反馈的结合, 故该算法能够解决全局环境未知时的轨迹规划问题。另外, 规划窗口目标位置的选取会影响满足约束条件的算法的求解难度, 如图6所示, $P$ 为车辆的当前位置, 在道路边界约束下, $f_{1} f_{2}$ 为目标位置的选取范围, 若以直线上任意一点 $A~E$ 目标位置, 则规划出不同曲率的路径。若以 $B 、 C$ 为目标位置, 将不满足避障约束; 若以 $A$ 为目标位置, 将不满足侧向加速度约束, 通过判断确定 $PD$ 曲线为满足多项约束条件的最短路径。

	Figure Option View Download New Window
	图6 目标点的选取Fig.6 Target point selection

2.2 约束简化

智能汽车通过视觉系统检测到多个障碍物, 若将规划窗口中的所有障碍物不做区分, 并作为对轨迹的约束条件, 将降低算法的效率。为克服这一缺点, 本文引入了度量函数 $L (d_{i})$ 对障碍物进行分类。分类原则为:优先考虑距离车辆较近的障碍物对轨迹的安全约束, 障碍物距离当前车辆越远, 障碍物对轨迹的约束越弱。度量函数表达式如下所示:

$L (d_{i}) = \{\begin{array}{l} 0, 0 \leq d_{i} \leq d_{\min} \\ k \times d_{i} + b \leq 0, d_{\min} \leq d_{i} \leq d_{\max} \\ L_{\min} < 0, d_{i} \geq d_{\max} \end{array} (19)$

式中: $d_{i}$ 为规划窗口内每个障碍物相对于车辆的距离, $d_{i} = \sqrt{(x_{k} - x_{i})^{2} + (y_{k} - y_{i})^{2}}, (x_{k}, y_{k})$ 为车辆的当前位置坐标, $(x_{i}, y_{i})$ 为障碍物 $i$ 的位置坐标。

度量函数 $L (d_{i})$ 表示当前时刻规划出的轨迹点与障碍物之间的安全距离。由于本文用圆对车辆和障碍物进行包络, 属于较为保守的安全方案, 因此当障碍物距离车辆较近 $(d_{\min} \leq d_{i} \leq d_{\max})$ 时, 安全距离 $L (d_{i})$ 为0也能保证车辆与障碍物有一定距离; 当车辆与障碍物较远 $(d_{i} \geq d_{\max})$ )时, 安全距离 $L (d_{i})$ 为负值且随 $d_{i}$ 线性变化 $(L (d_{i}) = k \times d_{i} + b)$ 优点是在减弱较远障碍物对车辆约束的同时, 保证了车辆与该障碍物的安全距离随着相对距离动态变化; 当障碍物距离车辆足够远时, 安全距离为 $L_{\min}$ 且不发生改变, $L (d_{i})$ 与 $d_{i}$ 变化关系以及简化约束原理如图7所示。

	Figure Option View Download New Window
	图7 L(d_i)与d_i变化关系Fig.7 Relationship between L(d_i)and d_i

2.3 速度规划

通过上述规划方法可以得到满足动力学约束、初始状态及目标状态约束的路径, 为了保证车辆安全行驶, 需要规划车辆在该路径上的行驶速度, 即在车辆不失稳的情况下尽快通过该路径。为保证车辆在任意时刻都可以安全停车, 使每个时刻下的终止车速为0, 主要分为以下3个步骤:

(1)只考虑前轮不侧滑的条件下, 计算最大车速约束:

$v_{\max} = \sqrt{μg (1 + l^{2} κ^{2}) \sqrt{\frac{1}{κ^{2}} + l^{2}}} (20)$

式中: $μ 、 g$ 分别为静摩擦因数以及重力加速度; $l$ 为轴距; $κ$ 为不同路径点对应的曲率; $v_{\max}$ 为最大行驶车速。

(2)计算车辆的在路段下的行驶距离D, 即规划出的路径点的总长度:

$D = \overset{k = n}{\sum_{k = 1}} ‖ p_{k + 1} - p_{k} ‖ (21)$

式中: $p_{k} 为第 k 个路径点 (x_{k}, y_{k}), 共有 n$ 个路径点。

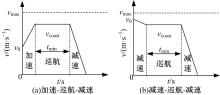
(3)计算巡航车速v_coast, 假设车辆加速度恒定, 则满足下式:

$D = \{\begin{array}{l} \frac{v_{coast}^{2} - v_{0}^{2}}{2 a_{accel}} + v_{coast} t_{\min} + \frac{v_{coast}^{2}}{2 a_{decel}}, v_{\max} - v_{0} \geq ε \\ \frac{v_{0}^{2} - v_{coast}^{2}}{2 a_{accel}} + v_{coast} t_{\min} + \frac{v_{coast}^{2}}{2 a_{decel}}, v_{\max} - v_{0} < ε \end{array} (22)$

式中: $a_{decel}$ 为减速段的减速度; $a_{accel}$ 为加速度段的加速度; $v_{0}$ 为当前车速; $ε > 0$ 表示当前车速与最高车速限值 $v_{\max}$ 的接近程度, $v_{\max} - v_{0} \geq ε$ 表示当前车速小于且远离最高车速, 可以执行加速-巡航-减速过程; $t_{\min}$ 为最短巡航时间; $v_{\max} - v_{0} < ε$ 表示当前车速接近最高车速, 需要执行减速-巡航-减速过程。规划出的速度曲线如图8所示。

	Figure Option View Download New Window
	图8 车速曲线Fig.8 Speed profile

设车辆行驶该段路径的总时间为 $t_{total}$ , 在 $v_{\max}$ 范围内对式(22)中巡航车速 $v_{coast}$ 进行遍历, 可得到不同 $v_{coast}$ 对应的总时间 $t_{total}$ , 选择 $t_{total}$ 最小值对应的巡航车速, 由此确定满足约束的车速曲线。

2.4 轨迹规划算法框架

算法流程图如图9所示。算法分为主规划、滚动窗口和寻优3个模块。主规划模块通过对比车辆当前位置与终点位置坐标判断是否需要启动轨迹规划算法。若启动规划算法, 在检测到障碍物的情况下根据车辆当前位姿信息以及环境信息进行轨迹寻优, 并更新当前步长下的轨迹。滚动窗口模块有两个主要功能:一方面在车辆的行驶过程中更新窗口内的环境信息; 另一方面, 在规划窗口滚动后, 获取当前车道满足约束的目标点的位姿信息。如果无法规划出满足各项约束的路径(例如无法避开障碍物), 需要紧急停车以保证车辆安全。

	Figure Option View Download New Window
	图9 算法流程图Fig.9 Algorithm flowchart

3 仿真验证

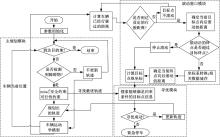
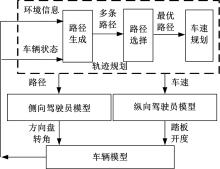
通过Simulink-CarSim软件搭建联合仿真平台, 在CarSim中设置道路边界、障碍物、车辆动力学参数及约束条件, 利用Sfunction(C语言)编写轨迹规划模块, 并搭建最优预瞄驾驶员模型^[15]。上述滚动窗口优化的轨迹规划问题是一个典型的非线性优化问题, 目前对该问题的求解通常转化为非线性规划问题。本文采用Matlab中非线性规划求解器对此问题进行求解, 模型原理如图10所示。

	Figure Option View Download New Window
	图10 轨迹规划算法模型搭建Fig.10 Model of trajectory planning

如图10所示, 轨迹规划模块在线接收障碍物信息和当前车辆状态信息, 通过滚动窗口优化算法得到最优可行轨迹, 并结合设定的预瞄时间计算最优侧向加速度和纵向期望车速, 驾驶员模型根据期望值决策出方向盘转角以及踏板开度并输入给CarSim车辆模型。

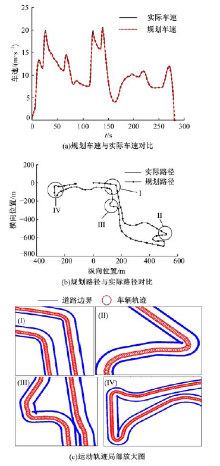
在蒙特卡洛赛道中验证算法的可行性, 设置道路宽度为7 m, 路面附着系数为0.7, 只允许车辆在道路边界内行驶, 故将道路边界当做障碍物处理, 车辆起始状态和终止状态分别为 $(x_{0}, y_{0}, θ_{0}, ϕ_{0}) = (0, 0, 0, 0) 和 (x_{f}, y_{f}, θ_{f}, ϕ_{f}) = (- 90, 0, 0, 0),$ 车辆主要参数如下所示:轴距为2340 mm; 长度为3550 mm; 宽度为1495 mm; 最小转弯半径为4.5 m; 极限前轮转角为29.79° ; 最大纵向加速度为7 m/s²; 最高车速为85 km/h。

仿真采用微型车, 车辆的对角线半长是1.92 m, 包络车辆的圆半径设为2 m。用于检测障碍物传感器检测半径设为20 m, 设a_y_max=4 m/s²时乘坐较为舒适^[8]。基于滚动窗口优化的在线轨迹规划结果如图11所示。

	Figure Option View Download New Window
	图11 蒙特卡洛赛道规划结果Fig.11 Result of Monte Carlo circuit

如图11所示, 轨迹规划算法能够生成满足车辆运动连续性要求的平滑轨迹, 轨迹跟踪最大侧向误差为0.3 m; 全程平均误差为0.12 m; 最大车速跟随误差为1.5 m/s; 全程平均误差为0.8 m/s, 故在目标工况内轨迹跟踪效果较好。同时, 车辆在与道路边界保证一定安全距离的情况下选择较近行驶路径, 例如直角弯中靠近道路内边界行驶, 典型情况如局部放大图(Ⅰ )所示; U形弯道中, 为保证不降低车速的情况下顺利通过, 则采用“ 切弯动作” , 典型情况如局部放大图(Ⅱ )所示; 在较短距离内通过多个曲率较大弯道时, 能够考虑多个弯道的特点并规划出可执行轨迹, 避免了传统规划方法的“ 振荡” 现象, 典型情况如局部放大图(Ⅲ )和(Ⅳ )所示。

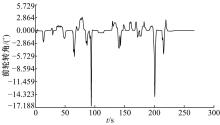
从图12可以看出:在蒙特卡洛赛道中, 前轮转角随时间变化较为平缓, 在接近100和200 s时, 车辆进入急转弯, 轨迹曲率分别为0.08、0.1 m^-1, 前轮转角分别出现较大值-16.0428° 、-14.8969° , 但并未超过极限值29.7938° 。

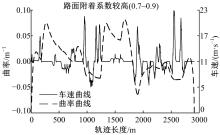
	Figure Option View Download New Window
	图12 前轮转角变化曲线Fig.12 Change curve of front wheel angle

为保证车辆不发生侧滑, 规划出的车速随轨迹曲率变化关系如图13所示。当曲率较小时, 车速较高, 最高可达22 m/s(75 km/h), 典型情况如图中轨迹长度为1200~1400 m段所示; 当曲率由0增加到0.07 m^-1时, 车速迅速下降的合理范围为4.7~10.6 m/s(17~38 km/h), 典型情况如图中轨迹长度为1800~2400 m段所示; 若轨迹曲率由较大值频繁变化, 考虑到行车安全, 车速先下降到较低值, 随后根据曲率变化逐渐增加, 典型情况如图中轨迹长度为1800~2300 m段所示。为进一步验证算法的避障功能, 恒定车速下要求车辆躲避多个障碍物, 试验结果如图14所示。

	Figure Option View Download New Window
	图13 车速与轨迹曲率关系Fig.13 Relationship between speed and curvature

	Figure Option View Download New Window
	图14 多障碍物环境中车辆运动轨迹Fig.14 Vehicle trajectory in multi-obstacle environment

结果表明, 本文方法在传感范围有限的情况下, 能够规划出曲率连续的避碰轨迹且满足多个约束条件。滚动窗口的引入有效结合了优化和反馈机制, 规划出的轨迹接近全局最优, 保证了全局的收敛性。

4 结束语

本文以未知环境下智能汽车轨迹规划为研究对象, 提出基于滚动窗口优化的智能汽车轨迹规划方法。用6次多项式描述路径曲线并将规划问题转化为求解 $a_{6}^{k}$ 的过程, 在此基础上, 进一步分析了不同约束对轨迹规划的影响, 给出了窗口局部子目标的选择方法, 并根据评价指标决策出当前规划窗口下的局部最优轨迹。在保证车辆不发生侧滑的前提下, 规划出随轨迹曲率动态变化的车速曲线。仿真结果表明:本文算法能够在具有多个障碍物的复杂环境中规划出连续光滑、满足各项约束条件且接近全局最优的轨迹, 为进一步优化模型以及动态未知环境下的轨迹规划研究提供了依据。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	Ziegler J, Bender P, Dang T, et al. Trajectory planning for Bertha—a local, continuous method[C]∥Intelligent Vehicles Symposium Proceedings, Dearborn, MI, USA, 2014: 450-457. [本文引用:1]
[2]	Turker T, Sahingoz O K, Yilmaz G. 2D path planning for UAVs in radar threatening environment using simulated annealing algorithm[C]∥2015 International Conference on Unmanned Aircraft Systems (ICUAS), Denver, CO, USA, 2015: 56-61. [本文引用:1]
[3]	Li G, Yamashita A, Asama H, et al. An efficient improved artificial potential field based regression search method for robot path planning[C]∥2012 IEEE International Conference on Mechatronics and Automation, Chengdu, China, 2012: 1227-1232. [本文引用:1]
[4]	Amiryan J, Jamzad M. Adaptive motion planning with artificial potential fields using a prior path[C]∥Rsi International Conference on Robotics and Mechatronics, Tehran, Iran, 2015: 731-736. [本文引用:1]
[5]	Syed U A, Kunwar F, Iqbal M. Guided autowave pulse coupled neural network(GAPCNN) based real time path planning and an obstacle avoidance scheme for mobile robots[J]. Robotics and autonomous systems, 2014, 62(4): 474-486. [本文引用:1]
[6]	Aamer N, Ramachand ran S. Neural networks based adaptive approach for path planning and obstacle avoidance for autonomous mobile robot (AMR)[J]. International Journal of Research in Computer Applications and Robotics (IJRCAR), 2015, 3(12): 66-79. [本文引用:1]
[7]	Montemerlo M, Becker J, Bhat S, et al. Junior: the stanford entry in the urban challenge[J]. Journal of Field Robotics, 2008, 25(9): 569-597. [本文引用:1]
[8]	Dolgov D, Thrun S, Montemerlo M, et al. Path planning for autonomous vehicles in unknown semi-structured environments[J]. The International Journal of Robotics Research, 2010, 29(5): 485-501. [本文引用:2]
[9]	Yao J, Lin C, Xie X, et al. *Path planning for virtual human motion using improved A star algorithm*[C]∥Seventh International Conference on Information Technology: New Generations, Las Vegas, NV, USA*, 2010: 1154-1158. [本文引用:1]
[10]	McNaughton M, Urmson C, Dolan J M, et al. Motion planning for autonomous driving with a conformal spatiotemporal lattice[C]∥2011 IEEE International Conference on Robotics and Automation (ICRA), Shanghai, China, 2011: 4889-4895. [本文引用:1]
[11]	Xanthidis M, Rekleitis I M, O'Kane J M. RRT+: fast planning for high-dimensional configuration spaces[J/OL]. [2017-04-02]. https:∥www.researchgate.net/publication/312222541_RRT_Fast_Planning_for_High-Dimensional_Configuration_Spaces. [本文引用:1]
[12]	González D, Pérez J, Milanés V, et al. A review of motion planning techniques for automated vehicles[J]. IEEE Transactions on Intelligent Transportation Systems, 2016, 17(4): 1135-1145. [本文引用:1]
[13]	Li Y, Shin B S. Internal Topology Based Flexible Shortest Path Planning Method for Indoor Navigation[M]. Berlin Heidelberg: Springer, 2015: 171-176. [本文引用:1]
[14]	Yang J, Qu Z, Wang J, et al. Comparison of optimal solutions to real-time path planning for a mobile vehicle[J]. IEEE Transactions on Systems, Man, and Cybernetics—Part A: Systems and Humans, 2010, 40(4): 721-731. [本文引用:1]
[15]	郭孔辉, 马凤军, 孔繁森. 人-车-路闭环系统驾驶员模型参数辨识[J]. 汽车工程, 2002, 24(1): 20-24. Guo Kong-hui, Ma Feng-jun, Kong Fan-sen. Driver model parameter identification of the driver-vehicle-road closed-loop system[J]. Automotive Engineering, 2002, 24(1): 20-24. [本文引用:1]

2014

0.0

... 除此之外,道路边界、交通规则以及驾驶员的驾驶习惯等也对轨迹规划提出了更高的要求^[1] ...

2015

0.0

... 针对多约束条件下智能汽车在未知环境中的轨迹规划问题,传统方法是将应用在机器人领域的轨迹规划算法用于生成车辆轨迹,例如人工势场法、模拟退火算法等^[2,3,4],这类方法具有结构简单、计算量较小的优点,但算法难以处理动态变化的驾驶环境且容易陷入局部最优解,限制了轨迹规划在智能汽车中的应用 ...

2012

0.0

2015

0.0

2014

0.0

2015

0.0

2008

0.0

... 文献[7,8,9]对上述方法进行了改进,如A^{#cod#x0002A ...}

2010

0.0

... 文献[7,8,9]对上述方法进行了改进,如A^{#cod#x0002A ...}

... 用于检测障碍物传感器检测半径设为20 m,设a_y_max=4 m/s²时乘坐较为舒适^[8] ...

2010

0.0

... 文献[7,8,9]对上述方法进行了改进,如A^{#cod#x0002A ...}

2011

0.0

2016

0.0

... 2 轨迹规划的约束条件汽车轨迹规划的两类最重要的约束为路径可行性约束和安全性约束^[12],可具体分为几何约束和运动学约束、道路边界约束以及车辆动力学约束 ...

2015

0.0

... 3 目标函数本文以路径最短作为性能指标,因此选取距离函数作为目标函数,通过求解目标函数在约束条件中的极值来确定点集的运动方程,最终使迭代路径点集趋于最优规划路径^[13]: ...

2010

0.0

... 由于车辆位姿在行驶过程中时刻改变,由式(18)易知,车辆需要根据车辆当前状态和周围环境的状态信息,考虑多个约束规划出可行的参考路径,综上述,轨迹规划的过程是随着车辆运动求取 a6k的动态规划过程^[14] ...

2002

0.0

. 2002, 24(1):20-24 DOI:doi:10.3321/j.issn:1000-680X.2002.01.005

Driver model parameter identification of the driver-vehicle-road closed-loop system

人-车-路闭环系统驾驶员模型参数辨识

Guo Kong-hui , Ma Feng-jun , Kong Fan-sen

郭孔辉, 马凤军, 孔繁森

基于在驾驶模拟器上进行的人-车路闭环系统仿真试验,使用全局演化局部寻优的辨识算法,对驾驶员模型进行参数辨识.通过大量的实际驾驶人员的试验数据,辨识出各种水平的驾驶员模型参数,为改进智能车控制系统的设计提供了依据.利用辨识得到的驾驶员模型和车辆模型进行了人-车路闭环系统的双移线与蛇行线仿真,仿真结果与试验数据具有很好的一致性.

... 3 仿真验证通过Simulink-CarSim软件搭建联合仿真平台,在CarSim中设置道路边界、障碍物、车辆动力学参数及约束条件,利用Sfunction(C语言)编写轨迹规划模块,并搭建最优预瞄驾驶员模型^[15] ...