引用本文
吴伟, 马万经, 杨晓光. 车路协同环境下基于路径的信号协调优化模型. 2014, 44(2): 343-351[WU Wei, MA Wan-jing, YANG Xiao-guang. Route based signal coordination control model within vehicle infrastructure integration environment. 吉林大学学报(工学版), 2014, 44(2): 343-351]  
Permissions
Copyright©2014, 吉林大学学报编辑部
版权所有.吉林大学学报编辑部
车路协同环境下基于路径的信号协调优化模型
吴伟, 马万经, 杨晓光
同济大学 道路与交通工程教育部重点实验室,上海 201804

吴伟(1987),男,博士研究生.研究方向:交通信息工程及控制.E-mail:201804_wuwei@tongji.edu.cn

基金:“863”国家高技术研究发展计划项目(2011AA110404); 国家自然科学基金项目(51178345,11272067);
摘要

基于车路协同环境下的动态路径流量、初始排队长度等信息及车辆-信号控制系统实时通信的运行环境,研究并建立了双向协调路径、车辆动态速度和交叉口配时参数的集成优化模型,克服了传统交叉口信号协调方法中路段行驶车速固定、受初始排队长度影响显著和不能优化协调路径的缺点。模型以协调路径流量与速度乘积最大为目标,以双向协调路径、相位差、车辆推荐速度等为决策变量进行优化,并建立了排队、车速、信号配时参数等一系列约束条件以确保集成优化解的可行性,从而实现了协调控制系统不停车通过量最大且延误最小的目的。与经典Maxband模型及Synchro软件的信号协调控制优化方案的比较表明,本文模型能够显著地提高绿波带宽,降低停车次数,提高协调效益。对路径流量波动、路段长度、最大限速及饱和度的敏感性分析进一步表明本模型能适用于不同的道路和交通条件,实时优化协调路径、车速及相位差。

关键词: 交通运输系统工程; 交通信号协调; 动态路径; 动态速度; 车路协同
中图分类号:U491.2 文献标志码:A 文章编号:1671-5497(2014)2-343-9
Route based signal coordination control model within vehicle infrastructure integration environment
WU Wei, MA Wan-jing, YANG Xiao-guang
Key Laboratory of Road and Traffic Engineering of the Ministry of Education, Tongji University, Shanghai 201804, China
Fund:
Abstract

Based on the real time information of dynamic route volume, initial queue length, and the real-time vehicle and signal controller communication within vehicle infrastructure integration environment, an route based integrated signal coordination control model is proposed to optimize the dual-direction coordinative routes, the dynamic travel speed, and the specific intersection signal timings. Thus overcomes the drawbacks of the conventional coordinated signal control model that uses those parameters as inputs based on the assumptions that the parameters are fixed and the value is optimal. The product of the output volume and the travel speed is employed as the objective of the propose model. The decision variables include the coordinative routes, travel speed and offset. A set of constraints were set up to ensure feasibility and safety of the optimal results. Compared with the results optimized by classical Maxband model and Synchro program, the proposed model can significantly improve the green wave bandwidth, decrease the number of stops, and increase total coordinated benefits. The sensitivity analyses with fluctuation of traffic flow, section length between intersections, maximum speed limit and degree of saturation further demonstrated the potential of the proposed model to be applied in various traffic conditions.

Keyword: engineering of communication and transportation system; traffic signal coordination; dynamic routes; dynamic speed; vehicle infrastructure integration
0 引 言

协调控制能降低协调路径上的延误及停车次数,提高车流平顺性,自Little[ 1]提出较实用的绿波带宽优化算法Maxband后,国内外大量研究学者以提高绿波带宽或降低交叉口延误等为目标[ 2],提出了基于数学规划[ 3, 4]和基于交通流动态演化[ 5, 6]的信号协调控制模型,并成功应用于SCOOT,SCATS和RHODES等交通协调控制系统中。由于传统控制环境下数据采集与信息交互的局限,以往大多协调控制模型将协调路径、初始排队长度、路段车速等作为固定参数输入[ 7],进行绿波优化。然而,正如Abu-Lebdeh等[ 8]指出,这种优化方法存在如下缺陷:①由于流量到达的波动性,在实际运行过程中,被输入的协调路径在很多周期内并非是最需要协调的路径;②初始排队长度对绿波控制效果有重要影响,其随机变化将导致绿波的效果降低甚至出现绿波无效果的情况;③车辆在路段上的真实行驶速度直接影响着实际的绿波宽度和协调效果。而在车路协同环境下,车辆能实时将行驶车速、路径、到达下游交叉口的时间等信息传送至信号控制系统,控制系统也能够将控制方案、建议车速实时传输给每一辆车,这为克服上述缺陷提供了基础数据和通信环境。Abu-Lebdeh[ 8, 9]等人首先探索了可变速度情况下对交叉口间协调能带来的效益,但其研究局限于在已知协调路径,且只对单向绿波进行优化,并没有提出系统的协调优化模型。

本文基于由车路协同环境实时准确的交叉口间的路径流量数据,建立双向协调路径、相位差和车辆速度的集成优化模型,克服传统模型的不足,提高交叉口信号协调效益。

1 模型参数定义

本文用到的主要参数及其定义如表1所示:

表1 关键参数及定义 Table 1 Key parameters and notation

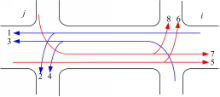
考虑相邻两交叉口 i、 j,如图1所示:

图1 交叉口间协调路径示意图Fig.1 Routes for coordination between intersection

假设无专用右转信号则有协调需求的路径共有8条,用 a表示从交叉口 i到交叉口 j(路径 a)的协调路径, b表示从交叉口 j到交叉口 i(路径 b)的协调路径, a∈{1,2,3,4}, b∈{5,6,7,8}。

2 优化模型
2.1 目标函数

本文的目标函数可表示为

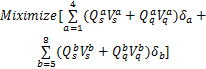
即本文的目标函数为双向协调路径的路径流量与行驶车速的乘积之和最大,其中路径流量包括饱和流量与非饱和流量。在此目标函数下,能确保协调相位更多的车流以更快的速度通过交叉口,提高通行能力并降低延误。

2.2 决策变量

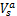
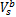
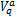
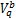
决策变量包括:相位差 Q ij, i方向选取的协调路径 δ a, j方向选取的协调路径 δ b,双向协调路径饱和车流车速 、 ,双向协调路径非饱和车流车速 、 。

2.3 约束条件

2.3.1 协调路径约束

假设每个优化时段双向各只选择一条协调路径,则

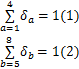
即从方向 i→ j的4条协调路径与方向 j→ i的4条协调路径中分别选择一条最优的协调路径。

2.3.2 流量守恒条件

以交叉口 i为例,假设在每个周期内进口道车流均匀到达,到达率为 q,交叉口饱和度小于1,则交叉口进口道绿灯期间的车辆通过率如图2所示:

图2 交叉口进口道车辆通过示意图Fig.2 Traffic flow clears the intersection

其中, s为饱和流量, t s为车流以饱和流量 s通过交叉口的时间, t q为车辆以到达率 q通过交叉口的时间, g i为有效绿灯时长, r i为有效红灯时长。则 t s、 t q的计算公式为

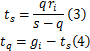
从图2可以看出,从上游交叉口某一相位驶出的车流可分为两部分:①在 t s内以饱和流量驶出,将此车流记作 f s; ②在 t q内以到达率驶出,记作 f q。

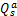
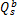
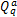
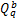
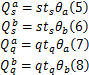
以 θ a、 θ b分别表示路径 a、 b的流量占交叉口进口道总流量的比例,则路径 a、 b某周期的到达流量可分别用 qC0 θ a和 qC0 θ b计算得出。进一步,路径 a、 b中车流 f s的流量 、 以及路径 a、 b中车流 f q的流量 、 可分别表示为

2.3.3 相位差约束

相位差约束为

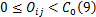
即相位差的取值需在0至周期之间,方向 i→ j的相位差确定后,能根据信号配时参数计算得到方向 j→ i的相位差。

2.3.4 速度约束

(1)饱和流速度约束

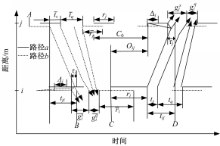
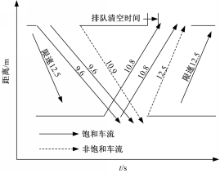
在车路协同环境下,应最大程度地引导车流 f s不停车且延误最小地通过下游交叉口,即最大程度地引导车流 f s行驶至下游交叉口最大排队点时,下游交叉口绿灯期间的启动波正好传至最大排队处,进而车流 f s跟随最大排队点处的车辆通过下游交叉口。对于非饱和车流 f q,则通过引导最大程度地使更多的交通流顺利通过下游交叉口。考虑上下游交叉口间协调路径 a和 b,双向车流的时空轨迹图如图3所示:

图3 上下游交叉口双向车流时空轨迹图Fig.3 Time-trajectory figure for both directions

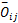
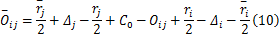
以路径 a协调方向的红灯起亮时间定义相位差 O ij,则相反方向路径 b的相位差 为

从图3可以看出,从时间点 A到时间点 B,有:

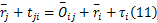
把式(10)代入式(11)并整理得:

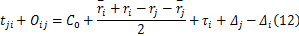
同样,从时间点 C到时间点 D,有:

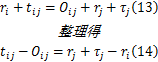
排队清空时间 τ i由两部分构成:一部分为启动波传递到最大排队长度点所需的时间;另一部分为从最大排队长度点行驶,直至通过交叉口所需的时间,可表示为

式中: W i为交叉口 i处启动波速; V i为交叉口 i处饱和车流通过交叉口的速度。

同样, τ j可表示为

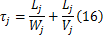
式中: W j为交叉口 j处启动波速, V j为交叉口 j处饱和车流通过交叉口的速度。

饱和车流 i→ j方向的路段行程时间 t ij同样由两部分构成:一部分为从上游交叉口 i到下游交叉口 j最大排队长度点的行驶时间;另一部分为从最大排队长度点跟随排队车辆行驶,直至通过交叉口所需的时间,可表示为

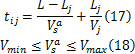
同样,有

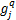
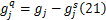
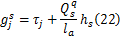
对于上游绿灯后期驶出的非饱和车流 f q的引导车速计算方法,以流向一为例,首先计算下游交叉口清空排队与饱和车流 f s后的绿灯剩余时间 ,从图3中可以看出:

的计算式为

式中: l a为路径 a的进口道车道数; h s为饱和车头时距。

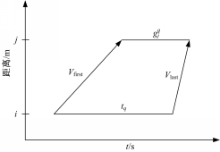
非饱和车流从交叉口 i到下游交叉口 j的时空轨迹图如图4所示:

图4 非饱和车流时空轨迹图Fig.4 Time-trajectory figure for non-saturation flow

图中, Vfirst表示非饱和车流的头车的引导车速, Vlast表示非饱和车流尾车的引导车速,则非饱和车流的平均车速为

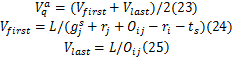
将式(24)(25)代入式(23)并整理得:

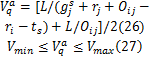
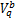
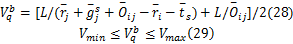
同理,方向 j→ i的非饱和车流车速 为

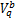
若由式(26)(28)计算得到的 、 不在区间 Vmin与 Vmax之间,则说明非饱和车流在本周期内无法通过下游交叉口,在计算目标函数时,将其值取为0。

综上,本文基于车路协同环境的路径流量、动态车速引导,建立交叉口间信号协调优化模型可表示为

目标函数:

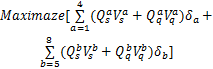
决策变量: O ij, , , , , δ a, δ b

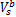
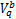
约束条件:式(1)~(29)

3 模型验证
3.1 实验设计

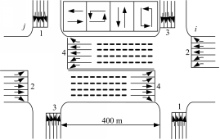
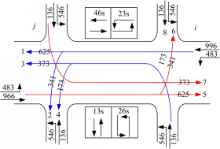
考虑两相邻交叉口 i与 j,交叉口间距为400 m,交叉口进口道编号、车道功能划分和相位相序如图5所示:

图5 研究区域参数配置图Fig.5 Basic layout of the study area

设置两交叉口的共同协调周期为120 s,每周期的总损失时间为12 s,饱和流量为1800 cpu/h,则饱和车头时距为2 s;设置路段车流合理的速度变化范围为4.7~12.5 m/s(17~45 km/h),启动波的传递速度为4.9 m/s,排队车辆平均车头间距为7.6 m。按各进口道的饱和度分配绿灯时间,首先设置各交叉口进口道的饱和度为0.7,考虑两交叉口双向各路径流量相等,两交叉口的路径流量分配及信号配时如图6所示:

图6 路径流量分配及信号配时图Fig.6 Traffic volumes for each route and signal timing

在此情况下,计算各路径的协调参数如表2所示:

表2 协调路径参数表 Table 2 Parameters for each route
3.2 模型结果对比分析

为验证本文模型的有效性,实证分析对比了3种方案的控制效果。方案1:Maxband优化方案。方案2:Synchro优化方案。方案3:本文模型优化方案。

在方案1与方案2中,路段行驶车速设置为最大值12.5 m/s,对比结果如表3所示:

表3　 优化结果对比表 Table 3 Comparison of results

从表3可以看出,本文模型的协调路径为路径1与路径7,而方案1与方案2都协调主流向路径1与路径5;各模型优化的相位差各不相同;在行驶车速方面,本文模型方案3的优化结果等于最大车速。通过每周期不停车车辆数的对比可以看出,本文模型能大幅提高协调路径车辆通过数。协调路径的绿波带宽、停车次数、不停车通过效益值的对比如图7、图8、图9所示:

图7 不同模型带宽优化对比图Fig.7 Comparison of green band width for different models

图8 不同模型停车次数优化对比图Fig.8 Comparison of number of stops for different models

图9 不同模型协调路径不停车通过效益值Fig.9 Comparison of mobility benefits for different models

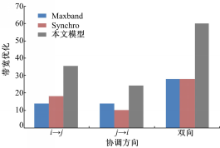
从图7可以看出,Maxband方案与Synchro方案双向拥有同样宽度的带宽,而本文模型优化方案则可以显著提高绿波带宽,对比Maxband方案与Synchro方案,本方案在方向 i→ j分别提高表3 优化结果对比表

绿波带宽154%和98%;本文方案在方向 j→ i分别提高绿波带宽75%和145%;双向共提高带宽115%。本文模型能大幅提高绿波带宽的原因在于协调双向路径1和路径7,而Maxband方案与Synchro方案则协调双向主流向路径1和路径5,双向协调主流向的弊端在于此方向协调成效会对另一个方向的协调造成负面影响,而本文模型则通过优化协调路径规避了此不足。

从图8可以看出,对比Maxband方案与Synchro方案,本文模型的协调路径停车次数很小,每小时双向协调路径停车次数能分别降低609次和639次。

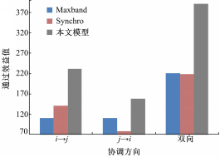
从图9可以看出,不论是方向 j→ i或方向 i→ j,本文模型的不停车通过效益值(由本文目标函数计算)比Maxband方案和Synchro方案都有明显提高。在双向协调路径上,虽然Maxband方案和Synchro方案都协调的是流量最大的主流向,但本文模型的不停车通过效益值最高,比Maxband方案和Synchro方案分别提高了77.7%和78.5%。

3.3 模型参数敏感性分析

3.3.1 路径流量波动敏感性分析

在相同的饱和度0.7下,从进口道1、2、3进入交叉口的流量不变,但考虑路径流量的波动,选取3种不同的路径流量方案进行对比分析。

情形1:假设某一周期从交叉口 i到交叉口 j的左转路径2的流量多于直行路径1的流量。在此将图6中路径1与路径2的输入流量互换,其他条件不变。

情形2:图6中所示方案。

情形3:双向左转路径2(路径6)的流量多于直行路径1(路径5)的流量。在此将图6中路径1与路径2的输入流量互换,路径5与路径6的输入流量互换。

模型优化结果如表4所示:

表4　 路径流量波动与模型优化值 Table 4 Fluctuation of volume for the route and the results of the model

从表4可以看出,路径流量改变后,本文模型选择的优化路径、相位差、路段速度随之改变,说明本模型具有随交通状态的变化动态优化上述参数的能力。情形1和情形3选择优化路径2和路径5,而情形2选择优化路径1和路径7。情形1和情形3协调路径2的饱和车流,为了避免停车,需以略低于最大速度的车速行驶,而非饱和车流则无法在本周期顺利通过交叉口。通过路径流量波动性的分析可以看出,本文模型能选择最佳的协调路径,选择的方法是通过计算目标函数——最大不停车通过率,并不仅仅从流量的大小进行选择,而更多地考虑双向相位差、行驶车速、是否停车等综合因素的影响。

3.3.2 路段长度敏感性分析

取饱和度为0.7,路径各参数参见表2,改变两交叉口间的路段长度,变化区间从100 m到800 m,模型优化结果如表5所示:

表5 路段长度改变与模型优化值 Table 5 Variation of section length and the results of the model

从表5可以看出,在给定的输入条件下,随着路段长度的变化,表4 路径流量波动与模型优化值双向协调路径的选择和相位差也随之改变;目标函数的取值并不随路段长度的变化表现出明显的趋势,值得注意的是,由于目标函数取值与路段行驶车速成正比,模型优化结果趋于选取更大的行驶车速,如最大限速12.5 m/s,但过高的行驶车速会存在一定的遇到红灯的概率,从而导致停车,特别是当优化双向路径时,需引导车流服从速度建议值获取最大的模型效益,以 L=700为例,饱和车流和非饱和车流服从不同的车速建议值降低车速后,所有车流能不停车顺利通过交叉口。其车流运行轨迹图如图10所示:

图10 本文模型效益时空分析图Fig.10 Time trajectory figure for proposed models

这正是本文模型的优势所在,通过对车流采用不同的速度引导值,保证最多的车流以最大的不停车速度通过下游交叉口。

3.3.3 路段车速敏感性分析

从前面的分析可以看出,本文模型在保证车流最大程度不停车的情况下选取最大路段行驶车速,因此改变路段最大限速的取值从8.3 m/s(30 km/h)至16.7 m/s(60 km/s),以 L=700为例,分析模型优化结果的变化,如表6所示:

表6 路段车速改变与模型优化值 Table 6 Variation of travel speed and the results of the model

从表中可以看出,随着路段最大限速的增大,目标函数取值随之增大;双向协调路径的选择与相位差的取值也随之改变;当单向如方向 i→ j路段行驶车速取最大限速时,方向 j→ i的速度取值则由于相位差的限制可能取较小值,如最大限速等于11.1 m/s(40 km/h)、15.3 m/s(55 km/h)或16.7 m/s(60 km/h)时。

3.3.4 饱和度敏感性分析

在其他条件不变的情况下,改变进入交叉口的进口道1、2、3的饱和度,选取3种不同的饱和度方案分析模型优化结果:①低饱和度方案,取饱和度等于0.5;②中饱和度方案,取饱和度等于0.7;③高饱和度方案,取饱和度等于0.9。

模型优化结果如表7所示:

表7 饱和度改变与模型优化值 Table 7 Variation of degree of saturation and the results of the model

从表中可以看出,随着饱和度的增大而路径流量比例不变的情况下,本文模型选择的协调路径将不会发生改变;相位差与行驶车速有较小的调整;目标函数值与不停车通过车辆数随饱和度的增大而增大。

4 结束语

建立了车路协同环境下基于路径的动态车速和相位差协调优化模型。基于车路协同环境下能提供的车辆的路径信息,实时动态优化交叉口间的协调路径、路段行驶车速及相位差,以实现协调效益的最大化。案例分析表明,本文模型相对于经典Maxband模型和Synchro模型,能显著提高绿波带宽,同时减少停车次数并增加不停车通过量。对路径流量波动、路段长度、最大限速及饱和度的敏感性进一步分析表明,本模型能适应不同的道路交通条件,动态优化协调路径、车速及相位差,由此进一步证明了本文基于路径的信号协调控制优化模型的优越性。

为了方便优化模型的建立,本文采用了车流到达率服从均匀分布的模型。实际上在车速协同环境下,可通过车/车路通信实地采集到的车流到达数据替代均匀分布模型,从而扩展了本文模型的适用范围。本文仅给出了协调路径、动态车速、相位差的实时优化方法,但选择何时优化并切换至新的优化结果,尚需进一步研究。

The authors have declared that no competing interests exist.

参考文献
[1] Little J D. The synchronization of traffic signals by mixed-integer linear programming[J]. Operations Research, 1966, 14(4): 568-594. [本文引用:1] [JCR: 1.786]
[2] Liu Y, Chang G L. An arterial signal optimization model for intersections experiencing queue spillback and lane blockage[J]. Transportation Research Part C-Emerging Technologies, 2011, 19(1): 130-144. [本文引用:1] [JCR: 2.006]
[3] 卢凯, 徐建闽, 李轶舜. 进口单独放行方式下的干道双向绿波协调控制数解算法[J]. 中国公路学报, 2010, 23(3): 95-101.
Lu Kai, Xu Jian-min, Li Yi-shun. Algebraic method of arterial road coordinate control for bidirectional green wave under signal design mode of one-phase-one-approach[J]. China Journal of Highway and Transport, 2010, 23(3): 95-101. [本文引用:1] [CJCR: 2.996]
[4] Parr S A, Kaisar E. Critical intersection signal optimization during urban evacuation utilizing dynamic programming[J]. Journal of Transportation Safety & Security, 2011, 3(1): 59-76. [本文引用:1]
[5] Hu P, Tian Z Z. A new approach to variable-band width progression optimization[C]∥89th Transportation Research Board Annual Meeting, Washington DC, 2010. [本文引用:1]
[6] Hajbabaie A, Medina J C, Benekohal R F. Traffic signal coordination and queue management in oversaturated intersections[R]. USDOT Region V Regional University Transportation Center Final Report, No. 047IY02, 2011. [本文引用:1]
[7] He Q, Head K L, Ding J. PAMSCOD: Platoon-based arterial multi-modal signal control with online data[J]. Transportation Research Part C: Emerging Technologies, 2012, 20(1): 164-184. [本文引用:1] [JCR: 2.006]
[8] Abu-Lebdeh G. Integrated adaptive-signal dynamic-speed control of signalized arterials[J]. Journal of Transportation Engineering, 2002, 128(5): 447-451. [本文引用:2] [JCR: 0.863]
[9] Abu-Lebdeh G, Chen H. Exploring the potential benefits of Intellidrive-enabled dynamic speed control in signalized networks[C]∥89th Transportation Research Board Annual Meeting, Washington DC, 2010. [本文引用:1]