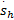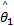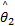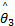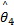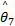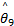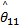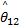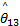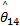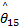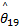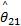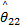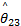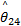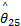韩京元(1973),男,博士研究生.研究方向:控制工程学,智能控制.E-mail:hankw11@163.com
针对非线性板球系统中小球的镇定和跟踪控制问题,提出了一种采用结合系数的自适应解耦模糊滑模控制器设计方法。将板球系统分解成4个子系统,分别对每个子系统定义了滑模面,利用结合系数将滑模面结合,基于Lyapunov稳定性理论,构造了自适应模糊规则来调节滑模结合系数,从而实现了板球系统的稳定控制,并避免了复杂的计算。本文对所提出的控制方法进行了板球系统的仿真实验验证。仿真结果表明,此方法能够较好地实现非线性不确定系统的镇定控制和轨迹跟踪问题。
A design method of decoupling adaptive sliding mode controller unsing integrated factor is proposed for trajectory tracking and stabilization control of the Ball and Plate System (BPS). In this approach, the nonlinear system is decomposed to four subsystems and the state response of each subsystem is designed by a corresponding sliding surface. In the design, the integrated factor is adopted to combine the sliding surface, which is decided by an adaptive fuzzy algorithm based on the Lyapunov stability theory. Thus the stability of the system is guaranteed and the complex calculation is avoided. The proposed design method is applied to investigate Ball and Plate Vision System. The simulation results demonstrate that the proposed approach is effective in resolving the stabilization control and trajectory tracking control tasks of nonlinear and under-actuated system with uncertain terms.
板球系统是一个典型的非线性系统,20世纪具有强耦合、欠驱动和无约束的特点[ 1, 2]。80年代末许多学者以板球实验装置作为被控对象进行各种控制算法的研究,用于检验非线性控制算法的性能[ 3, 4]。1989年,Hauser利用近似线性化模型完成了对实际板球系统的控制,Zhang提出了T-S模糊算法和分层控制算法[ 5, 6, 7]。Hauser等的控制方法是基于近似线性化模型提出的,在控制器设计上具有局限性[ 5]。多步的李雅普诺夫函数比较复杂,反步法容易出现因高阶非线性系统计算量增加而导致的微分爆炸现象[ 8]。上述方法没能充分考虑板球系统的不确定性、强耦合和外部干扰等因素[ 9, 10]。如果不确定性的范围超出了控制器所设计的给定界限值,系统的稳定性将不能保证。针对板球系统存在的不确定性、强耦合和滞后等非线性特性,文献[ 1, 4, 11, 12, 13]提出了对非线性对象数学模型精度要求不高的人工智能方法和切换方法。
在这类模型不确定系统的控制领域中,滑模控制器(SMC)是一种有效的非线性控制方法[ 14, 15]。应用SMC方法在滑模表面调节非线性系统的动态特性时,系统对于其系统的不确定性和摄动等具有不变的特性。但是SMC也存在切换增益过大和抖振的缺点[ 15, 16]。
针对具有未建模特性的非线性系统,模糊逻辑控制器(FLC)是一种能够克服系统不确定性的有效控制器[ 3, 13, 17]。但模糊逻辑控制器也存在如下缺点:①系统的阶次越高则规则总数越多;②隶属函数的参数设计直接影响模糊系统的控制指标,而隶属函数的选取需要相当长的时间;③不能利用一般的稳定性分析工具分析模糊系统的稳定性。最近十五年以来,人们提出了模糊滑模控制器(FSMC)的概念[ 18, 19, 20]。结合FLC和SMC的FSMC提供简单的FLC设计方法,其方法保持着良好的SMC特性,同时减少了抖振,并能够使控制系统渐近稳定。文献[16,19]提出了较好的非线性解耦特性的模糊滑模解耦控制器的设计方法,采用中间变量结合两个状态表面,并利用一个控制器实现其对象的稳定控制。但是,其中间变量数需经过试错过程才能得到。而不合适的耦合参数会降低系统的控制性能,甚至引起系统的不稳定。
本文针对上述存在的问题,提出了利用多层自适应模糊滑模控制策略的解耦控制器的设计方法,分别进行小球的镇定控制和轨迹跟踪控制仿真实验验证。该方法将非线性耦合系统分解成几个子系统,定义每个子系统的滑模表面,设计解耦多层滑模控制器,采用自适应模糊推理算法来选择和调节滑模表面的耦合系数,并利用Lyapunov函数推导控制规则,从而保证控制系统的渐近稳定性。
二阶非线性系统的规范状态空间模型:
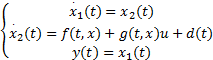 | (1) |
式中: x=( x1, x2)T为状态变量; f( x)和 g( x)为非线性函数; u为控制输入; d( t)为多种干扰和摄动的综合量,并假定综合干扰是有界的。
线性函数(滑模表面)定义如下:
s =λ x1+ x2(2)
式(2)表示滑模表面当前状态的代数距离,式中 λ为正实数。当综合干扰不存在时,系统(1)的动态特性可表示为:

选择 λ,使式(3)的根的实数部分小于零,则该系统是稳定的。当 d( t)=0时,通过滑模稳定条件 
ueq= 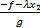
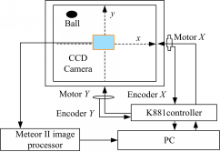
图1和图2所示为吉林大学控制理论与智能系统实验室自主开发的板球实验装置BPVS-II的原理图和小球的运动坐标系。板球系统利用步进电机驱动平板的两个自由度产生可控姿态,使小球在平板上稳定跟踪期望运动轨迹。同时CCD摄像头和图像视觉系统用于测量小球的位置信息[ 1, 4, 16]。
假设小球和平板一直接触,始终保持滚动运动而无滑动,板球系统的状态方程为[ 4]:
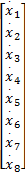 = =  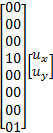 | (4) |
式中:输入、输出变量分别为:
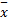
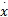



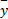
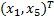
式中: B=m/( m+Jb /R2); M=[ x1 
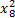


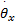

板球系统的状态方程(4)可表示为:
 | (7) |
式中:d i(t, 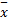
定义滑模表面为:
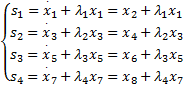 | (8) |
式中:λ1,λ2,λ3,λ4是大于0的常数,定义f i( 
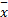
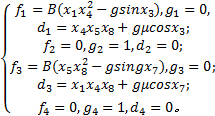 | (9) |
假定X轴和Y轴之间的耦合项和不确定性项小于正常数d i。式(7)系统模型可按X轴和Y轴分成为两个系统,即:
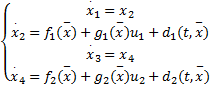 | (10) |
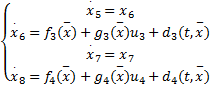 | (11) |
因此,板球系统的X轴和Y轴可以分别进行独立控制,结合小球在两个轴上的运动状态,小球在平板上的运动控制状态也可以检测。
依据式(10), X轴的状态方程可表示为:
 | (12) |
式中: 
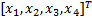
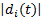
式中:di max和 ε i均为大于零的常数。
X轴的状态方程式(12)可分解为状态( x1, x2)和( x3, x4)两个二阶子系统。在一个控制输入 u x( t)的作用下,同时调节状态( x1, x2)和( x3, x4),最终 X轴可获得稳定控制。针对两个子系统,分别定义滑模表面为:
 | (13) |
式(13)的动态方程如下:
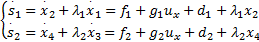 | (14) |
如果式(14)中没有综合干扰,即d2=0,按照滑模条件 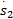
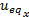 = =  | (15) |
该控制规则仅考虑子系统( x3, x4),而没有考虑子系统( x1, x2)。为了能够同时考虑两个子系统的状态,定义结合两个滑模表面的滑模面为
s x= s2- 
式中: 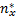
滑模表面(16)的微分式如下:
 = = 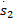  | (17) |
由式(16)可知,选择多种条件下相对应的结合系数 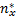


R i:If s x =A i1 and 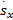
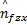
式中: R i是第 i个模糊规则( i=1,2,…, r); C i是利用 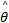
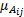

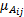
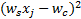
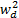
式中: wc为中心参数值; wd为中心点 wc到模糊隶属函数值为0 .5的点坐标值间的距离, w s为 x j的系数。
最优结合系数的估计值的模糊输出为:
 ( s x, ( s x, 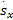 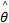 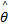 | (20) |
式中: 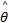
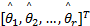

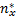
根据通用近似定理[ 14],存在最优模糊逻辑系统,表示为:
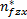

式中:非时变参数矢量 θ *定义为:
θ *= 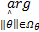
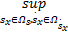
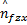

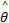

式中:M θ, 
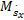
令 τ x≡ 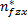

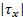
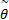
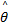
由式(14)可知,当 d≠0时,系统存在耦合和干扰。此时 X轴的控制律为:
u x= ueq x+ uvs x (24)
式中: ueq x与式(15)相同; uvs x为综合摄动和耦合项的控制律。
由式(16)和(23),定义 Lyapunov函数为:
V( s x,
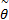 )= )= 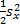  | (25) |
式中: α为正数。由式(14)(16)(23)和(24),能够得出 Lyapunov稳定条件:
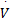
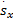
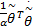
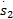
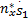
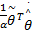


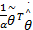

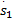
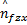
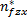



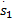
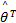
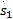
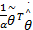
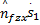



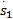
uvs x=[ 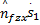
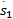
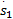
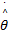
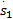
式中: sgn()为符号函数,则式(26)可表示为:

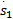


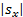
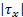
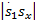
如果自适应法则式(28)不满足 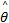


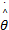 = =  | (30) |
 ( s x, ( s x, 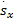 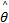  | (31) |
由 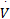
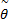
结合式(15)(27),可得 X轴控制律如下:
 | (32) |
对于上式中的结合系数 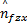

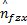
同理,针对 Y轴,可得相应的控制律如下:
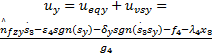 | (33) |
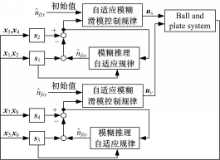
一般来说,为了抑制控制信号的抖振,可将符号切换函数换成饱和函数。同时可以将此方法推广到高阶系统。综上可得,板球系统的解耦自适应模糊滑模控制系统框图见图3。
由式(9)~(11),通过对X轴和Y轴的控制能够实现小球在平板上的镇定控制和轨迹跟踪控制。板球系统BPVS II的参数如下:小球的质量m为0.263 kg;小球的半径 rb为0.02 m;小球的重力加速度g为9.8 m·s-2;小球的转动惯量 Jb为4.2×10-5 kg·m-2。
由式(18)调整结合系数,定义隶属函数(见图4)的中心点为-1.5、-0.5、0、0.5和1.5,每个隶属函数的 ws和 wd分别定为1和1 /0 .15。利用表1中构造的模糊推理系统调整参数 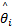

| 表1 模糊推理规则 Table 1 Fuzzy inference rules |
参数Mθ,Ms, 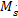
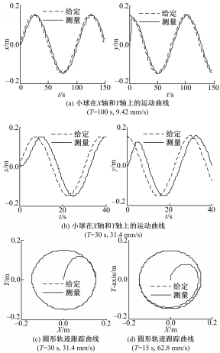
在镇定控制的仿真试验中,小球从初始位置( x0, y0)=(150 mm,150 mm)到达坐标原点的镇定控制仿真结果如图5所示,这里最优结合系数为 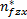

由图5可知,状态变量都具有较好的性能,小球收敛到坐标原点并在原点稳定。从初始点到达原点的时间是6 s,同时小球可以获得35.4 mm/s的较高速度。由|x(4)|<0.005,|x(5)|<0.2,|x(8)|<0.005,|x(1)|<0.2,可以得到:|x(1)x(4)x(8)|≤5×10-6,|x(4)x(5)x(8)|<5×10-6,比参数d(d=0.01)小很多,因此,该方法有效地补偿了系统的不确定性、摄动和外部干扰等。
在轨迹跟踪实验中,系统采用与上述镇定控制相同的系统不确定性和干扰条件。
圆形轨迹跟踪仿真实验结果如图6所示。图6(a)为小球运动速度为9.42 mm/s的仿真结果;图6(b)(c)为小球运动速度为31.4 mm/s的仿真结果;图6(d)为小球运动速度为62.8 mm/s的仿真结果。给定信号为:

在仿真时,仍加入幅值为15 mm的随机测量干扰,作用于X轴和Y轴位置输出信号上。由图6(a)的仿真结果可知,X轴位置偏差为0.00194 mm,Y轴位置偏差为0.023 mm,圆形轨迹跟踪平均误差为0.023 mm;由图6(b)(e)的仿真结果可知,X轴位置偏差为0 .202 mm, Y轴位置偏差为0 .0507 mm,圆形轨迹跟踪平均误差为0 .201 9 mm;由图6( d)可知,当小球的速度为62 .8 mm/s时,平均误差为2 .54 mm。从仿真结果看,小球的速度越大,系统误差越大。
文献[ 16]采用符号距离模糊滑模控制方法(DFSMC[ 16])跟踪圆形轨道,半径与本文的方正实验一样,小球的速度是15 mm/s时,位置偏差大约是3~10 mm,小球的速度是55 mm/s时,位置偏差大约是8~20 mm。
从仿真结果可知,本文提出的解耦自适应模糊滑模控制方法,能够使板球系统状态变量始终保持在合适范围内,即获得较小的位置偏差,相比符号距离模糊滑模控制方法效果更好。
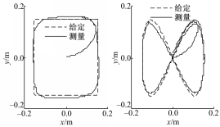
图7为小球速度在40 mm/s以上的方形轨迹跟踪和8字形轨迹跟踪仿真实验结果。实验结果表明,本文提出的控制器可使小球在板球系统中跟踪多种图形。
研究了一类非线性、不确定、欠驱动系统的控制问题。针对板球系统,提出了解耦自适应模糊多层滑模控制方法,并进行了仿真实验。当小球的速度为31.4 mm/s时,系统的平均位置偏差仅为0.2 mm。从实验可以看出,解耦自适应模糊多层滑模控制方法能够有效解决非线性系统的不确定性、强耦合和外部干扰等问题。如何能更合理地决定滑模表面的系数是以后需要进一步研究的问题。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|
| [20] |
|
| [21] |
|