刘厚德(1984),男,博士研究生.研究方向:空间机器人.E-mail:liuhoude84@163.com
首先对自旋目标的运动特性和运动预测问题进行了分析,并采用无损卡尔曼滤波(UKF)方法对目标当前运动状态进行估计,在此基础上对目标未来时刻运动状态进行预测。提出了一种基于预测速度补偿的自旋目标自主捕获路径规划方法,并对所提方法进行了数值仿真,仿真结果表明了方法的可行性和有效性。
First, the motion characteristics and motion prediction of the spinning target are analyzed. Then, the Unscented Kalman Filter (UKF) is used to predict the motion state of the target. On this basis, a method of autonomous path planning of a free-floating space robot for target capturing is proposed, which is based on motion prediction and speed compensation. Simulations are carried out to verify the feasibility and validity of the proposed method.
空间机器人在轨服务技术已成为我国乃至世界各航天大国解决航天器在轨维护、轨道垃圾清理等问题的重要技术[ 1, 2, 3]。目前已开展的在轨演示验证项目中,操控目标均为三轴稳定的受控合作目标。针对自旋目标的捕获问题尚无成功案例,目前仅处于理论研究[ 4, 5, 6, 7, 8]和地面试验验证阶段[ 9, 10]。当在轨服务技术面临工程实现阶段时,对自旋目标运动特性及自主捕获路径规划问题的研究是必不可少的,也是开展在轨服务任务仿真和试验验证的前提和基础。
自旋卫星上的捕获点相对于空间机器人存在一定的线速度和角速度。通常采用视觉伺服方法进行捕获操作,通过视觉测量得到相对位置和相对姿态关系,以规划机械手末端的运动轨迹。由于图像处理和位姿解算需要耗费一定的时间,机械手获取到的相对位姿信息实际上是过去时刻机械手末端和目标捕获点间的关系,空间机器人规划时的期望位姿相对于目标的实际位姿存在一定周期的延时。因此,针对静止目标捕获的路径规划方法,将难以直接应用到对运动目标的捕获。要解决此类问题,就需要基于测量信息,对目标的运动规律进行预测,在此基础上采用基于预测的路径规划方法来实现对自旋目标的捕获。
在以往的研究中多是将目标简化为绕固定轴旋转的刚体,将问题简化为平面情况。或者侧重于目标捕获后如何利用机械臂自运动实现空间机器人基座的稳定,对自旋目标三维空间运动的预测及自主捕获规划问题研究较少。本文首先对在轨服务任务中自旋目标的运动特性进行分析,采用适合于非线性系统的无损卡尔曼滤波器对其当前运动进行估计。在此基础上提出了一种基于预测速度补偿的目标自主捕获路径规划方法。
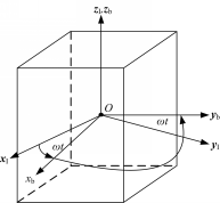
在轨服务的目标主要为故障的人造卫星,设O为星体质心,Ox by bz b为固联于星体的坐标系, xb、 yb、 zb为沿坐标轴的单位矢量;设 OxI yI zI为不旋转的空间飞行器参考坐标系, xI、 yI、 zI是沿坐标轴的单位矢量。在 t=0时刻, Oxb yb zb与 OxI yI zI重合,此后 Oxb yb zb以角速度 ω绕 OzI旋转,转角为 ωt, ω在本体坐标系中的分量为 ω x, ω y, ω z,卫星简化为刚体示意图如图1所示。
假设图1所示的各坐标轴都与通过质心的主惯量轴一致,定义卫星绕这些轴的主惯量分别为Ix、Iy、Iz,在此本体主轴坐标系中,惯量积等于零。卫星姿态自由转动的欧拉动力学方程在Ox by bz b中的分量可表示为:
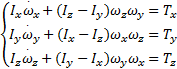 | (1) |
假设卫星关于Oz b对称,即Ix=Iy=I,且所受外力矩为0,则式(1)可表示为:
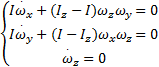 | (2) |
令ωz=ω s= const,ω p=( 
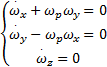 | (3) |
假设初始状态有:
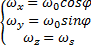 | (4) |
则
ω=
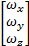 = = 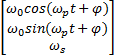 | (5) |
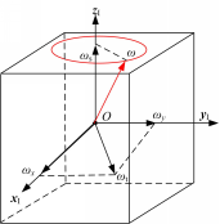
由式(5)可以看出星体运动的特点:在星体坐标系中,角速度分量 ω x, ω y周期性地变化,周期为2π /ωp,其合成速度 ωt绕 OzI轴旋转,转速为 ω0,因此星体的瞬时转速 ω绕轴 OzI作圆锥运动,其示意图如图2所示。
实际在轨航天器是非轴对称的,其轴向转动与横向转动间相互耦合,自旋速率 ωs不再恒定不变,主惯量轴的锥运动在空间形成的图案也将比较复杂。同时,由于空间环境的复杂性和多变性,实际在轨航天器将受到多种空间力矩的干扰,其运动特性比上面分析的情况复杂得多。因此,往往需通过其控制系统进行实时的姿态调整。而自主捕获任务中的目标主要为故障航天器,姿控系统不能正常工作,它们在失控后将逐渐起旋,章动角处于周期性的变化之中,运动规律较为复杂。例如,在1990年9月3日成功发射的风云一号( B)气象卫星,于1991年2月14日因受空间高能粒子轰击后而在较长时间内工作紊乱,卫星姿态失控起旋, 逐渐地自旋速度达到59.88°/s,章动角达到40°[ 11]。
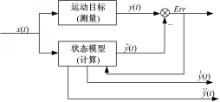
失控或者非合作的目标,其运动状态无法通过自身的传感器直接获取,需要根据外部设备提供的测量信息进行解算或者估计而间接得到。目前常用的测量设备仅能提供相对位姿信息,无法直接解算出相对速度和加速度信息,此时需要基于已有测量信息采用估计算法得到目标运动状态量的估计值。目标运动预测的思路为:首先根据经验和先验知识建立目标运动的状态模型,设定状态量x(t);然后分别通过测量和状态递推的方式获取运动目标运动状态y(t)和预测模型输出 

四元素对姿态角的表示范围非常大,不存在奇异问题,算法全局稳定,且在手眼视觉测量下,可以直接根据相对姿态矩阵反求四元数,因此本文采用四元素来描述自旋目标的姿态。
将姿态四元素及目标角速度定义为系统的状态量,即:
X=[ q, ω]T(6)
定义系统的状态量测量为:
Z= qT=[ q1, q2, q3, q4]T(7)
式中: q=[ q1, q2, q3, q4]T为航天器的姿态四元素; ω=[ ω x, ω y, ω z]T为目标相对星体坐标系的角速度分量。
由航天器动力学方程很容易获得四元素与角速度间的关系:
ω=2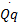 | (8) |
式中: Q为由四元素分量组成的四维正交旋转矩阵,表达式为:
Q=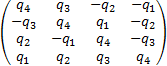 | (9) |
则四元素的导数 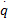
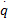

将式(10)展开为矩阵形式为:
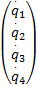 = = 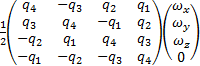 | (11) |
由自旋目标动力学方程(1)可得:
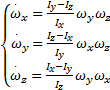 | (12) |
由式(11)和式(12)可知,系统运动方程存在非线性关系,其方程可表示为:
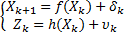 | (13) |
式中:δ k和υ k分别为扰动噪声和测量噪声,假定均为零均值高斯噪声,方差分别为 R和 Q; f( X k)由式(11)和式(12)组成;h( X k)= CX k,其中:
C=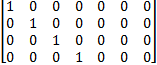 | (14) |
根据自旋目标的运动状态和量测方程,采用适当的预测算法可以获得目标相对于测量的下一时刻运动状态量:姿态四元素和角速度。
常用的预测和估计方法有最小二乘法和卡尔曼滤波法。最小二乘法是依据目标点的历史信息,通过预测目标的运动趋势,得到目标的预测值,但其依赖于过去的运动信息,计算中需要较大的存储容量。卡尔曼滤波算法模型简单,并且计算量较小。其在递推的过程中,只需考虑前一个时刻的信息,而不依赖于所有以前的信息,因此能够满足较高的实时性要求。无损卡尔曼滤波通过无损变换,能够将非线性模型展开至泰勒三阶式,且不需将非线性系统线性化,因此可以得到对非线性系统更好的估计结果,是目标非线性系统较为常用的方法。根据自旋目标运动状态方程和量测方程的特点,本文采用无损卡尔曼滤波对自旋目标的运动进行预测,以获取目标的预测速度。3 自旋目标自主捕获路径规划方法
空间机器人动力学建模和控制方面的重要研究成果见文献[12-13],典型的单臂空间机器人由 n自由度机械臂和作为其基座的航天器平台组成,其微分运动学方程可写成:
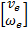 = Jb = Jb 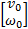 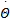 | (15) |
式中: ve、 ωe分别为基座质心处的线速度和角速度; Θ∈ R n为关节角( n为机械臂自由度数); Jb为与基座运动相关的雅可比矩阵; Jm为与机械臂运动相关的雅可比矩阵。
利用自由漂浮空间机器人动量守恒方程可得基座速度和角速度与关节角速度之间的关系为:
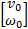 =- =- 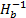 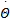 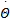 | (16) |
式中: Jbm为基座-机械臂雅可比矩阵。
将式(16)代入式(15),得到自由漂浮模式下空间机器人系统的运动学方程为:
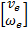 = Jb = Jb 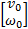 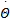 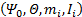 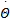 | (17) |
式中: Jg为空间机器人的广义雅可比矩阵,它是基座姿态、机械臂关节角以及各刚体质量、惯量的函数。
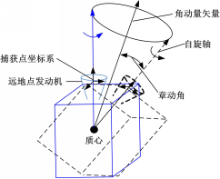
自旋目标简化模型如图4所示,以远地点发动机喷嘴为捕获对象,在远地点发动机内定义一个捕获点,并在捕获点处建立坐标系,作为自主捕获操作的目标坐标系。 t时刻,目标如实线部分所示, t2时刻,目标如虚线所示。抓捕时,要求机器人末端和抓捕手柄间相对速度和相对位姿误差足够小。因此自旋目标的捕获问题等同于机械臂末端追踪捕获点的问题。当机械臂末端工具坐标系与捕获点坐标系间的误差足够小时,认为目标捕获成功。
基于上述的估计结果,期望的末端运动速度按式(18)进行规划:
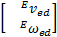 =K =K 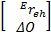 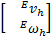 | (18) |
式中: ved、 ωed和 vh、 ωh分别为机械臂末端的期望速度、角速度和目标的绝对速度、角速度在坐标系 åE中的表示; K为比例系数; Δ O为姿态指向误差(即捕获点坐标系相对于机械臂末端坐标系的姿态),其计算公式为:
Δ O= ( ne ×nh +oe ×oh +ae ×ah)= ( ne ×nh +oe ×oh +ae ×ah)= 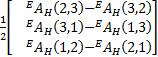 | (19) |
式中: 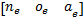
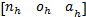
根据相对运动原理,目标的绝对运动速度为:
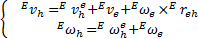 | (20) |
式中: E 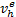
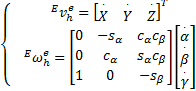 = = 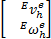 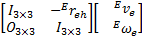 | (21) |
根据式(20),目标的运动速度为:
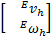 | (22) |
根据自由漂浮空间机器人的微分运动学方程,有:
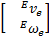 =( E Jg) =( E Jg) 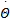 | (23) |
式中: E Jg为机械臂的末端广义雅可比矩阵; 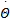
将式(23)代入式(22),有:
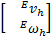 = = 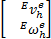 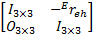 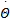 | (24) |
最后,根据式(24)和(18),可按式(25)规划机械臂末端运动速度:
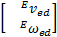 =K =K 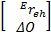 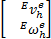 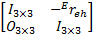 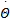 | (25) |
在实际运用中,一般不允许机械臂末端的运动速度过大,因此,在选择 K时要根据机械臂末端运动约束进行。
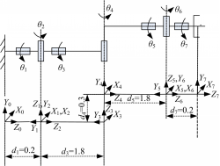
本文仿真用空间机器人系统由一个飞行基座、7 DOF机械臂和目标星组成。其中,机械臂的构型和相应的 DH参数分别如图5和表1所示。
| 表1 7DOF机械臂DH参数 Table 1 DH parameters of 7DOF manipulator |
假设目标航天器为轴对称的长方刚体,在它的一个面上安装有远地点发动机喷嘴。并以此喷嘴作为捕获操作的目标,目标航天器运动和捕获点选择示意如图4所示,目标航天器的尺寸及质量特性如表2所示。
| 表2 目标星尺寸及惯量参数 Table 2 Size and inertia parameters target star |
如图4所示,为了降低捕获难度,将捕获点选择在目标航天器的自旋轴上。以目标的质心为原点,3个主轴为坐标轴建立目标星本体坐标系,则捕获点本体坐标系的原点位于星体坐标系的主轴上,且姿态与目标星本体坐标系姿态相同。当目标星自旋时,捕获点相对于星体坐标系无转动,由于目标的章动,使得捕获点绕空间角动量轴做圆周运动。
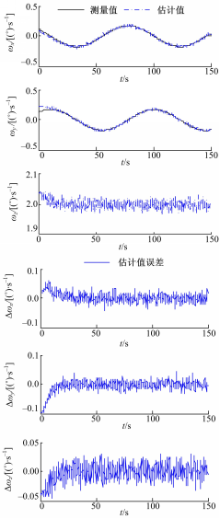
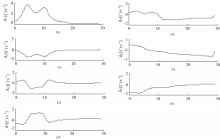
假设目标的章动角为5°,初始角速度为ω0=[0.1237i 0.1237j 2.0k]° /s;初始姿态四元素为q0=[0.33780.3686-0.10910.8591];相对应的估计初值为[ ω0 q0]T;方差误差初值为 dig[10-610-6 10-6 10-610-8 10-8 10-8];目标运动过程中,假设过程噪声和量测噪声分别为 dig[10-6 10-6 10-6 10-6 10-8 10-8 10-8]和 dig[10-6 10-6 10-6 10-6],则利用 UKF对目标的速度进行预测,估计结果如图6所示。由图6可知,目标速度的变化规律为:自旋速度的大小基本为常值,横向速度按照三角函数周期性变化,速度变化规律与第2节的自旋目标运动特性分析的结果相符,且估计误差在合理的范围之类,可以满足预测路径规划需求。
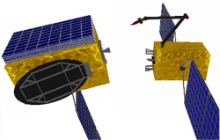
基于上述的初始条件和预测的目标速度,采用本文的预测路径规划方法,利用上述空间机器人系统对此自旋目标的捕获任务进行数学仿真,仿真初始时刻和终止时刻,空间机器人和自旋目标的位姿关系分别如图7和图8所示。
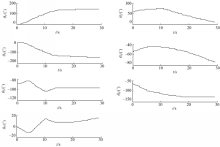
目标捕获过程中,机械臂末端工具坐标系和捕获点坐标系间的位姿关系如图9所示,空间机器人的关节变量和关节角速度分别如图10和图11所示。
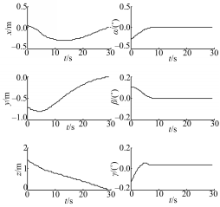 | 图9 机械臂末端和捕获点间相对位姿关系Fig.9 Relative position and orientation of between the robot arm end and capture point |
由图10可知,机械臂末端与捕获点之间的相对位姿逐渐趋于稳定。其中,相对位置趋于0;与自旋轴间的相对姿态趋于0,在自旋轴方向的姿态欧拉角存在固定大小的误差(由于目标绕自旋轴旋转,机械臂末端设置了速度限制,无法跟踪上其姿态变化)。在实际工程应用中,可以忽略此方向的姿态同步,在锁紧目标后采用相应的控制策略可实现复合体系统的稳定。
首先对在轨服务任务中自旋目标的运动特性进行了分析,并建立了其运动的状态方程和量测方程,然后采用适用于非线性系统的无损卡尔曼滤波器对其未来时刻运动状态进行预测。在此基础上提出了一种基于预测速度补偿的目标自主捕获路径规划方法。该方法在对机械臂末端进行运动规划时将目标的预测速度补偿进去,较好地解决了由于图像处理及位姿解算耗时所带来的规划滞后问题,可实现对运动目标的自主捕获,为后续的在轨服务任务研究和仿真积累了经验。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|