作者简介:许芳(1987-),女,博士研究生.研究方向:模型预测控制及FPGA技术.E-mail:xufang11@mails.jlu.edu.cn
针对快速动态系统对模型预测控制(MPC)的微型化和高实时性的需求,提出了一种MPC控制器的现场可编程门阵列(FPGA)硬件实现方法。MPC中的二次规划(QP)问题采用粒子群优化(PSO)算法进行求解。通过分析算法的特点,对算法计算步骤进行循环展开、流水线等优化处理,充分利用FPGA的硬件并行计算特性提高MPC的在线计算性能,最终得到MPC控制器的最优实现方案。最后以电子节气门的跟踪控制为例,在实验平台上进行了实时仿真实验,验证了基于FPGA硬件实现方法设计的MPC控制器的有效性和实时性。
Miniaturization and high computational performance are demanded when Model Predictive Control (MPC) is applied to fast dynamic system. In order to meet these requirements, a novel hardware implementation method for MPC on a Field Programmable Gate Array (FPGA) chip is proposed. The Particle Swarm Optimization (PSO) algorithm is employed to solve the Quadratic Programming (QP) problem formed in MPC. By analyzing the characteristics, the MPC algorithm is optimized by parallelism-loop unrolling and pipelining to obtain an optimal MPC controller. Real-time simulation tests of electronic throttle control are performed to verify the MPC controller. The results show that the proposed scheme can improve the computational performance of MPC.
模型预测控制(Model predictive control,MPC)的优化过程是在有限采样时间间隔内反复在线求解优化问题,如何在有限的采样时间内快速准确地求出最优解是MPC应用于快速动态系统所面临的一大挑战。为提高预测控制的在线求解速度,国内外学者从以下两个方面进行了研究:一是在预测控制算法和优化算法方面,文献[ 1, 2]采用粒子群优化(Particle swarm optimization,PSO)算法求解模型预测控制中的二次规划(Quadratic programming,QP)问题,可快速得到全局最优值;文献[ 3, 4]提出了一种显式MPC算法,在线时通过查表确定当前时刻状态所在区域即可得到相应的控制率;文献[ 5>]提出利用QP问题的特殊结构求解优化问题,使得算法在线求解速度是普通优化算法的100倍。二是在硬件实现方面,文献[ 6- 9]提出了基于片上可编程系统(System on programmable chip,SoPC)的嵌入式方案,采用软硬件结合的方式实现MPC控制器。文献[ 10- 12]提出现场可编程门阵列(Field programmable gate array,FPGA)全硬件方案,采用新型高级程序设计语言或硬件描述语言(Hardware description language,HDL)进行MPC算法描述,利用硬件并行方法提高算法的在线计算性能。
随着设计复杂度的不断增加,传统寄存器传输级的FPGA设计方法已无法满足要求,基于高级综合(High level synthesis,HLS)工具的设计方法被越来越多的设计所采纳[ 13, 14]。HLS将高级语言转换为HDL语言,可使开发者专注于算法设计而不是寄存器传输级电路,可大大降低FPGA的开发难度。因此本文基于HLS设计方法,提出一种兼顾FPGA并行计算和HLS开发简便特点的MPC控制器硬件实现方法。由于PSO算法是一种随机的、并行的优化算法,其并行的结构为硬件并行计算提供了有利条件,因此选用PSO进行QP问题的求解。最后以电子节气门跟踪控制为例,验证FPGA硬件方法实现的MPC控制器的实时性。
MPC的控制策略为多步预测,滚动优化和反馈校正,其机理可以简要描述为:在每一采样时刻,根据获得的当前量测信息和预测模型预测被控对象的未来动态,在线求解一个有限时域开环最优控制问题,优化序列的第一个元素作用于被控制对象直至下一个采样周期。这个预测-优化-反馈的过程在每个采样时刻重复进行[ 15]。
考虑如下的线性时不变时间系统的状态空间增量模型:
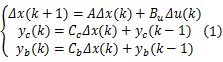
式中:状态增量 Δx( k) =x( k) -x( k-1),维数为 nx;控制输入增量 Δu( k) =u( k) -u( k-1),维数为 nu;被控输出量 yc( k)的维数为 nc;约束输出量 yb( k)的维数为 nb; A、 Bu、 Cc和 Cb是相应维数的系统矩阵。
设预测时域为 p,控制时域为 m,且 m≤ p,根据状态模型(1)可以分别推导出被控输出和约束输出预测方程:

式中: Sx, c、 Su, c、 Ic、 Sx, b、 Su, b和 Ib是与系统矩阵 A、 Bu、 Cc和 Cb相关的参数矩阵。
考虑到系统的时域约束,线性约束MPC的优化问题可以描述为:

满足约束:
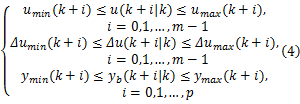
其中目标函数为:
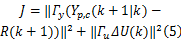
优化问题中 R( k+1) =[ r( k+1),…, r( k+p)]T为参考输出序列; Ty和 Tu为加权矩阵; ΔU( k)为优化问题的独立变量,即优化控制序列,定义如下:
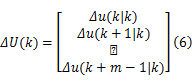
由于约束条件的存在,约束线性预测控制的优化问题一般没有解析解,因此,通常是将这种优化问题转化成QP问题,并采用数值方法进行求解。根据模型(1)及其预测方程(2),约束优化问题(3)(4)(5)可以转换为如下标准QP问题:
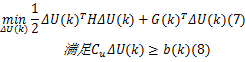
式中: H是Hessian矩阵; G( k)是梯度向量; ΔU( k)是优化独立变量; Cu和 b( k)是相应的约束条件参数矩阵。 H和 G( k)由下式计算:
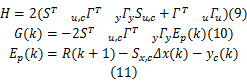
常用求解QP问题的方法主要有积极集法和内点法,这两种算法都是串行的迭代算法,每一次迭代都是基于上一次所得的结果,在此基础上出发,寻找更加优秀的解,它们并不具备多大的并行加速空间。而PSO算法各个粒子在迭代过程中互相不依赖,可以完全实现并行化处理,因此本文选用PSO算法进行QP问题(7)(8)的求解,得到的闭环控制增量为:
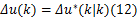
PSO中每个优化问题的解都是搜索空间中的一只“鸟”,称之为“粒子”,所有的粒子都有一个由被优化的函数决定的适应值(Fitnessvalue),每个粒子还有一个速度决定它们飞翔的方向和距离,然后粒子们就追随当前的最优粒子在解空间中搜索[ 16, 17]。
PSO的工作原理为:首先初始化一群随机粒子(随机解),然后通过迭代找到最优解,在每一次迭代中,粒子通过跟踪两个“极值”来更新自己,第一个就是粒子本身所找到的最优解,即粒子历史最佳位置,这个解叫做个体极值,记作 Pj,另一个极值是整个种群目前找到的最优解,即群体历史最佳位置,这个极值是全局极值,记作 Pg。假设粒子的空间维数为 D,第 j个粒子位置表示为 D维向量 Xj=[ xj,1, xj,2,…, xj, D];粒子移动速度表示为 Vj=[ vj,1, vj,2,…, vj, D];粒子历史最佳位置表示为 Pj=[ pj,1, pj,2,…, pj, D];群体历史最佳位置表示为 Pg=[ pg,1, pg,2,…, pg, D]。则PSO的速度和位置更新公式如下:

式中: t为迭代次数; j=1,2,…, N, N代表种群大小; r1和 r2为[0,1]区间的随机数; c1和 c2为加速度权重系数; w为惯性权重。
MPC的一大优点就是能够显式处理时域约束,为了处理MPC的约束条件(8),本文在每次更新粒子位置后,判断新产生的粒子位置 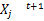
原则1 如果更新后的粒子位置 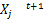

原则2 如果 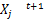
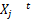
原则3 如果 
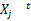
根据MPC算法的原理可知,MPC每次在线优化求解时都会计算得到未来 m步的最优控制序列,即[ Δu( k|k),…, Δu( k|k+m-1)],并且只有第一步 Δu( k|k)作用于系统,因此,将剩余的 m-1步控制序列作为粒子群最优位置 Pg的初始值,即 Pg=[ Δu( k|k+1),…, Δu( k|k+m-1), Δu(0)],其中 Δu(0)为控制增量的初始值,这样可以大大提高PSO的求解效率。
PSO 算法实现流程如下:
Step1 初始化粒子群。令 t=0,随机初始化粒子群位置 X及粒子的个体最优位置 Pj,全局最优位置初始化为 Pg=[ Δu( k|k+1),…, Δu( k|k+m-1), Δu(0)]。
Step2 根据式(13)(14)更新粒子的速度和位置。
Step3 判断更新之后的粒子位置是否满足约束,如果满足约束,转步骤Step5;如果不满足则转步骤Step4。
Step4 按照约束处理策略确认更新之后的粒子位置。
Step5 根据适应度函数,即QP问题的目标函数(7),更新个体最优位置 Pj和全局最优位置 Pg。
Step6 如果到达最大迭代次数,则停止,输出最优解;否则转Step7。
Step7 令 t=t+1,转Step2。
粒子群的维数 D等于MPC的控制时域 m,粒子的适应度函数为MPC算法QP问题的目标函数(7),则基于PSO的MPC算法流程如下:
Step1 初始化MPC算法的相关参数矩阵 Sx, c、 Su, c、 Ic、 Sx, b、 Su, b、 Ib、 H和 Cu,并给定参考序列值 R( k+1)。
Step2 在 k时刻,获得状态测量值 x( k)和输出测量值 yc( k),计算 G( k)和 b( k)。
Step3 利用PSO算法求解QP问题(7)和(8),获得最优控制序列 ΔU*( k),则 ΔU*( k)的第一个分量为系统最优控制增量,即 Δu( k) =Δu*( k|k)。
Step4 将控制量 u( k) =u( k-1) +Δu( k)作用于系统。
Step5 令 k=k+1,转Step2。
本文采用基于FPGA的硬件实现方法进行MPC控制器的设计。为了能够充分利用硬件的并行计算特点,在控制器的硬件设计之前,需要对控制算法的计算过程进行分析,以找出算法关键计算步骤。针对耗时的计算,进行循环展开、流水线等优化处理,以提高算法在线计算性能。
MPC在优化过程中,需要在每个有限的采样时间内在线求解优化问题,得出最优控制序列,但优化问题的求解过程复杂,存在大量的矩阵运算,如在线更新 G( k)和 b( k)时,运算中涉及到的矩阵以及矩阵维数如下: Su, c的维数为 ncp×num, Sx, c的维数为 ncp×nxm, H的维数为 num×num等。如果增大MPC的控制时域 m及预测时域 p,则矩阵维数随之增加,算法的计算量就会大幅度增加。如果能够将这些矩阵运算并行化,将会大大提高在线计算速度。
PSO算法中主要包含三个嵌套的循环体:外层的循环体主要控制粒子群的每一代的进化,直至最大迭代次数,每个循环之间有先后关系,不能进行循环展开,因此考虑使用流水线进行加速;中间层的循环主要控制当代的粒子位置更新,直至最大粒子群数,各个粒子之间相互独立,但粒子群数一般较大,因此考虑使用局部循环展开或流水线进行加速;内层的循环主要控制单个粒子的更新,单个粒子的维数为控制时域长度 m,一般较小,而且是并行的,因此使用完全展开进行加速。
基于FPGA的MPC控制器设计流程如图1所示。首先在MATLAB中进行PSO-MPC的算法描述,并进行离线仿真验证;其次将算法的M语言描述转换成C/C++描述,并根据数据的范围设计定点数据模型;然后进行算法的循环展开、流水线的优化处理,并设置时序、微架构的约束,获得MPC控制的最优实现方案,利用Catapult C转换成HDL描述;对MPC的HDL描述进行功能仿真验证,功能验证通过后进行编译、综合、布局布线得到FPGA配置文件;最后进行控制器的板级验证,如果控制器不满足设计要求,则对定点模型、算法优化处理或布局布线设置进行修改,直至控制器设计满足要求,获得最优控制器。
3.2.1 控制算法描述
先将PSO-MPC算法在MATLAB中进行算法的编写和描述,然后进行离线仿真验证。
3.2.2 随机数的设计
MATLAB验证通过后,需要将PSO-MPC算法的M语言描述转换成C/C++描述。PSO算法粒子群的初始位置是随机初始化的,在MATLAB中使用的是随机数生成函数rand(),但是硬件实现时,Catapult C不支持rand()函数,因此需要设计随机数的产生函数。本文采用线性同余法产生[0,1]区间的随机数,随机性来源于取模运算,其递推公式如下:
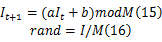
式中: I0为初始种子; a为乘法器,满足 a≥0,且为整数; b为增值,满足 b≥0,且为整数; M为模数,满足 M≥ I0, a, b;mod为取模运算。如果 b=0,称之为乘同余法,速度更快,也可产生长的随机序列。
3.2.3 定点数据模型的设计
为了提高算法的计算性能,减少资源消耗,本文应用定点数据模型代替浮点数据模型。根据Catapult C提供的定点数据模板,如表1所示,进行算法的定点数据模型设计。
| 表1 Catapult C支持的定点数据类型 Table 1 Fixed-point data types provided by Catapult C |
表1中, W代表数据的位宽, I代表整数位的位宽, true表示有符号数据, false表示无符号数据。通过算法分析,根据不同变量的变化范围,合理地设计其数据类型,通过精确的位宽控制可以在不影响精度的前提下减少资源的消耗,提高计算性能。例如随机数在[0,1]区间,整数位和符号位都是不必要的,只需要足够的小数位保证精度就可以了;串口接收到的数据都是16 bits的整数,小数位就是不必要的。
3.2.4 算法优化
Catapult C综合主要包括算法优化处理,ModelSim功能仿真验证和分析结果报告的生成。为了提高算法计算性能,算法的优化主要包括数据存储结构的选取,循环展开及流水线,加速库的使用等。
(1)数据存储结构的设计
数据的存储结构有多种,例如RAM存储,寄存器(Register)存储。如果多个数组变量使用一个RAM存储,不同变量之间存取时不能同时进行,数据存取速度慢,但是这种存储方式消耗的FPGA硬件资源少;如果每个数组变量使用单独的RAM存储,那么不同变量之间的存储就不受RAM的限制,数据存取速度较快,但是消耗的FPGA硬件资源较多;如果数据变量使用寄存器进行存储,数据的存取完全不受RAM的限制,数据存取速度最快,为并行性提供了有利条件,但同时消耗的硬件资源也最多。因此,为了获得最优计算性能,在硬件资源充足的情况下,本文选取了寄存器存储结构。
(2)循环展开及流水线
控制算法性能的优化很大一部分都依赖于对循环代码的处理。逻辑上没有数据依赖性、存储结构为寄存器的循环代码,可以选择完全展开或部分展开。循环代码完全展开,算法计算性能最优,但消耗的硬件资源最多;循环代码部分展开,算法计算性能较高,消耗的硬件资源也相对较少。计算性能和硬件资源消耗相互矛盾,需要进行尝试,折中取最优方案;另外对逻辑上具有依赖性的循环代码,可以进行流水线处理,加快算法计算速度。本文在线计算 G( k)时使用了流水线结构,PSO算法的内层循环完全展开,中间层循环采用了流水线结构。
(3)加速库的使用
通过使用Altera加速库可以使设计者能够迅速实施MPC算法,并且能够得到较好的效果和较低的面积。设计者只需通过在算法的源程序中添加包含加速库的头文件,就可以使用加速库中包含的各种函数实现MPC中的复杂运算。加速库内的函数在综合的时候直接映射到Altera的专用硬件资源上。加速库提供了一些常用的算法函数,如乘累加运算、乘加运算、开平方根运算、桶形移位寄存器等。
3.2.5 性能报告分析
将优化后的PSO-MPC的C/C++代码转换成Verilog HDL代码后,Catapult C会生成一个计算性能和资源占用的结果报告,包括电路所占用的面积,电路的延时(Latency)和吞吐量(Throughput),以及电路的时序余量(Slack)。根据这个报告,就可以查看控制器设计是否满足性能、资源以及时序要求,如果不满足,就需要修改C/C++代码或约束添加直到控制器设计满足要求为止。
3.2.6 ModelSim功能仿真验证
为保证生成的HDL代码功能的正确性,需要进行功能仿真验证。Catapult C支持C/C++语言描述测试激励,自动调用ModelSim对生成的PSO-MPC的Verilog HDL代码进行功能仿真,因此测试激励编写容易,而且可以复用,简化了功能验证。
3.2.7 板级验证
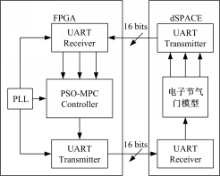
本文基于FPGA开发板和dSPACE实时仿真系统进行MPC控制器的板级验证,测试平台示意图如图2所示。由示意图可知,需要通过RS232串口实现FPGA开发板和dSPACE的数据通信,因此,还需要编写RS232通信接口的Verilog HDL代码,按照16 bits原码形式接收和发送数据,同时使用PLL IP核为整个电路提供精准时钟。最后将PSO-MPC算法的HDL代码和RS 232,PLL集成,进行编译综合、布局布线,得到FPGA配置文件并下载到开发板中进行板级验证。
本文搭建的实时仿真实物平台如图3所示。平台主要由FPGA开发板、dSPACE实时仿真系统和两台PC机构成,其中FPGA开发板(DE3 Stratix III)完成控制器的硬件实现,运行MPC控制算法,dSPACE实时仿真系统则模拟被控对象,运行电子节气门数学模型,PC1运行FPGA的开发软件Quartus II,通过JTAG下载线与FPGA开发板相连,用来进行MPC控制器的开发和设计,PC2运行ControlDesk软件,通过PCI接口与dSPACE系统相连,对实验结果进行监控和测试。使用该平台可以对本文设计的基于FPGA的MPC控制器进行仿真、测试及验证。
本文以文献[18,19]介绍的电子节气门系统为被控对象,以电子节气门跟踪控制为例进行实时仿真实验,验证本文设计的基于FPGA全硬件方案实现的MPC控制器的功能和实时性。电子节气门控制系统的目标是节气门开度能够又快又精确且超调尽可能小地到达期望目标位置。根据文献[18,19]推导的电子节气门模型,进行简化得到节气门系统的状态方程如下:

式中: x=[ x1, x2]T为系统的状态变量,其中 x1是电子节气门的开度(rad), x2是节气门角速度(rad/s);选取状态 x1为系统输出 y;控制量输入 u为电子节气门直流电机两端的电压(V)。
实验参数的选取如下:预测时域 p=20,控制时域 m=2,采样时间 Ts=1 ms,加权矩阵 Ty和 Tu都选为相应维数的单位矩阵,使用PSO求解优化问题,PSO中的迭代次数和粒子数都设置为50,粒子维数 D=2。FPGA选择EP3SL150F1152,速度等级为2,时钟设置为50 MHz。
为了得到MPC控制器的最优FPGA实现方案,本文对控制算法进行了不同的优化约束处理,不同FPGA优化方案下的MPC计算性能比较结果如表2所示。表2中延迟周期数和延迟时间表示PSO-MPC算法在线计算时间;硬件资源指的是控制器所需的硬件资源消耗,单位为查找表(Look up table,LUT);时序裕度正值代表生成电路满足时序要求,负值则不满足时序要求。
表2中对比了V1、V2和V3三种优化方案,V1是无优化的算法,V2是优化变量的存储结构,V3是进行算法循环展开和流水线优化方案。方案V1耗时2.76696 ms,占用6527个LUT;方案V2使用寄存器(Register)存储变量,数据可以并行存取,耗时1.10168 ms,硬件资源消耗38446个LUT,虽然硬件资源消耗相对较多,但V2计算性能相对于V1提高了1倍。方案3在方案2的基础上,对控制算法进一步优化,将PSO算法中的单个粒子更新进行完全展开,同时对种群循环和迭代循环进行流水线设计。方案V3耗时0.22772 ms,相对于方案V1计算性能提高10倍,相对于方案V2计算性能提高5倍。方案V3占用硬件资源39960个LUT,与方案V2相比多占用了1500个LUT,比方案V1资源消耗增加了5倍,虽然占用硬件资源最多,但是仍在FPGA芯片允许的硬件资源范围内。
由表2的3种方案计算性能比较可以得出,方案V3具有最优的计算性能,因此,本文选择方案V3进行MPC控制器的实现。
| 表2 不同FPGA优化方案下的MPC计算性能的比较 Table 2 Comparison of computational performance of MPC under different optimization schemes on FPGA |
表3对采用不同实现方案的MPC控制器的计算性能进行了简单比较,主要包括Visual Studio软件方案,文献[8]中的FPGA/SoPC方案和本文的FPGA硬件实现方案。其中Visual Studio中软件计算的PC配置为:英特尔Pentium(奔腾)G620@2.60 GHz双核处理器,内存为4 GB(金邦DDR3 1333 MHz)。
由于每种方案采用的优化算法、时钟频率、开发板型号等不一样,因此,表3是进行了大致的计算性能比较。由表3结果可知,本文基于FPGA全硬件方案实现的MPC控制器具有最优的计算性能。
由于软件实现MPC控制器时是用C语言编写的代码,C程序是顺序执行的,而本文实现方案中的硬件语言Verilog HDL是并行执行的,因此本文实现方案计算性能0.228 ms相对于软件实现方案9.599 ms提高了约40倍;文献[8]中的FPGA/SoPC方案采用的是嵌入式实现方案,并采用自定制指令提高在线计算速度,采用软硬件结合的方式实现控制器,C程序是串行,硬件语言Verilog HDL是并行执行,而本文实现方案都是采用硬件语言Verilog HDL代码,因此计算性能优于FPGA/SoPC方案,除此之外对偶算法求解过程复杂,计算步骤之间耦合性强,不利于程序的并行运行,而PSO算法的并行结构为硬件并行计算提供了有利条件,因此本文方案的计算性能0.228 ms是FPGA/SoPC方案计算性能0.342 ms的1.5倍。
基于以上对几种不同实现方法下的MPC计算性能的比较分析可知,本文基于FPGA全硬件方案实现的MPC控制器具有最优的计算性能。
| 表3 不同实现方法下的MPC计算性能比较 Table 3 Comparison of computational performance of MPC under different implementation methods |
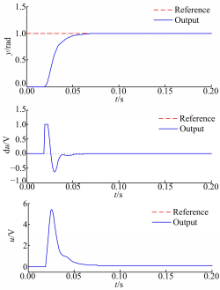
本实验将方案V3实现的MPC控制器在图3所示的基于FPGA和dSPACE的实时仿真平台上进行电子节气门跟踪控制实验。MPC控制器的控制量为电压,控制增量为电压变化量,通常控制驱动芯片对电压值和电压值的变化量都有一定的阈值要求,因此,控制量和控制增量的约束分别选取为-6 V< u( k)<6 V和-1 V<Δ u( k)<1 V。节气门开度期望值为1 rad的阶跃响应实验曲线如图4所示。
由图4可以看出,控制量和控制增量都没有超出约束范围,满足约束条件;系统输出能够在50 ms内快速跟踪上期望值并稳定在期望值附近,系统无超调,满足了节气门的控制要求,因此,本文设计的基于FPGA硬件实现方案的MPC控制器具有很好的实时性能,并且能够很好地实现电子节气门的跟踪控制。
从MPC的硬件实现角度出发,研究了MPC控制器的快速实现方法,提出了一种新的基于FPGA硬件实现方案。该方案结合硬件并行计算的高实时性和HLS开发的简便特点,提高了MPC算法的在线计算性能,缩短了控制器开发周期。利用PSO算法实现了约束MPC算法QP问题的优化求解。通过算法分析及不同优化方案下MPC计算性能的对比,得到了具有最优计算性能的MPC控制器,并将该控制器用于电子节气门的跟踪控制,在搭建的实时仿真平台上进行了实验测试,实验结果表明,基于FPGA硬件实现的MPC控制器能够很好地实现电子节气门的跟踪控制。目前的工作实现了线性MPC控制器的FPGA硬件实现,下一步将针对非线性被控系统,学习非线性MPC算法,并完成非线性MPC控制器的FPGA硬件实现。
| [1] |
|
| [2] |
|
| [3] |
|
| [4] |
|
| [5] |
|
| [6] |
|
| [7] |
|
| [8] |
|
| [9] |
|
| [10] |
|
| [11] |
|
| [12] |
|
| [13] |
|
| [14] |
|
| [15] |
|
| [16] |
|
| [17] |
|
| [18] |
|
| [19] |
|