基于混合交通流的车辆换道行为

引用本文

魏丽英, 吴荣华, 王志龙, 朱建辉. 基于混合交通流的车辆换道行为. 吉林大学学报: 工学版, 2014, 44(5): 1321-1326[WEI Li-ying, WU Rong-hua, WANG Zhi-long, ZHU Jian-hui. Lane-changing behavior based on mixed traffic flow. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(5): 1321-1326] 复制到剪切板

Permissions

基于混合交通流的车辆换道行为

魏丽英, 吴荣华, 王志龙, 朱建辉

北京交通大学交通运输学院, 北京 100044

作者简介:魏丽英(1974-),女,副教授,博士.研究方向:交通流理论及交通仿真建模.E-mail:lywei@bjtu.edu.cn

基金:“973”国家重点基础研究发展计划项目（2012CB725403）; 国家自然科学青年基金项目(71101008); 中央高校基本科研业务费项目（2012JBM057）; 国家留学基金项目

摘要

采用元胞自动机模型研究了城市交通中车辆的换道行为。在模拟非对称换道规则下混合交通流中的车辆换道行为中,通过增加公交车影响因子这一换道动机,分析了公交车对社会车辆换道行为的影响。分析结果表明:公交车的存在增加了车流中车辆的换道概率,且当道路处于中低密度状态时,社会车辆换道概率随公交车比例上升而增加,相应路段平均车速降低。在考虑了公交车影响因子后发现,公交车影响因子的存在会明显降低车辆换道概率。

关键词: 交通运输系统工程; 换道行为; 混合交通流; 公交车影响因子; 元胞自动机

中图分类号:U491.2 文献标志码:A 文章编号:1671-5497(2014)05-1321-06

Lane-changing behavior based on mixed traffic flow

WEI Li-ying, WU Rong-hua, WANG Zhi-long, ZHU Jian-hui

School of Traffic and Transportation, Beijing Jiaotong University, Beijing 100044, China

Abstract

This article studies the lane-changing behavior of vehicles in urban traffic using cellular automata model. In the simulation of lane-changing behavior in mixed traffic flow under asymmetric lane-changing rules, the impact of buses on the lane-changing behavior of social vehicles is analyzed by adding transit influencing factors as term of motivation. Results show that the presence of buses increases the lane-changing probability of social vehicles. Under the condition of low traffic density, the lane-changing probability of social vehicles with the bus ratio, and at the same time the average speed drops in corresponding road sections. In addition, when considering the bus influencing factors, the lane-changing probability obviously decreases.

Keyword: engineering of communications and transportation system; lane changing behavior; mixed traffic flow; bus influencing factor; cellular automata

Show Figures

0 引言

为了满足日益增长的交通需求,缓解交通压力,公共交通已成为城市交通系统中不可或缺的一部分。由于受自身体积、车速及停靠接驳行为等诸多因素的影响,公交车的运行特点与其他社会车辆有着明显差异。这种差异将影响到城市交通流中其他车辆的运行行为及通行效率。学者们曾采用多种方法对公交车给城市交通流带来的影响进行过深入的研究。由于公交车运行速度通常比社会车辆低,有公交车的交通流常表现出不同的稳态与亚稳态特性^{[ 1]}。因此,通过仿真建模的方式对城市公交车与社会车辆混行车流进行分析是了解混合交通流运行状态的一种有效手段^{[ 2]}。当前,多数学者把关注点放在公交车停靠站对交通流的影响^{[ 3, 4, 5, 6]}以及包含公交专用道的车流行为研究上^{[ 7, 8, 9]},但对混合车流中公交车会如何影响车流中车辆换道行为的研究较少。

由于元胞自动机(Cellular automata,CA)模型具有高度的空间离散、时间离散、状态离散等特点,能通过制定演化规则来推演系统的运行规律,因此,被广泛应用于交通领域的模拟仿真中。Nagel和Schreckenberg于1992年提出的NaSch模型是最著名的交通流元胞自动机模型^{[ 10]}。为描述更丰富的车辆运行行为,学者们在NaSch模型的基础上提出了大量改进模型^{[ 11, 12, 13]}。但此类模型均未分析运行中的公交车对社会车辆换道行为产生的影响。本文建立了考虑公交车影响因子的多车道换道模型,标定了公交车影响因子的值,并在该模型的基础上模拟了多种状态下的交通流,分析了公交车对城市道路中车辆换道率、车流运行速度及换道行为的影响。

1 模型的构建

在城市道路中运行的车辆通常以小汽车和公交车为主,因此本研究在模型的构建中将车辆的类型简化成公交车和小汽车两种车型。通常情况下,公交车机动性较差,速度低于小汽车,而体积大于小汽车。通过对小汽车体积的统计发现,两厢车的平均车长在4.2 m左右,三厢车平均车长为4.5 m左右(少量豪车及加长车除外)。同时,通过对北京市公交车进行统计发现,在单车厢公交车中个别车长为6 m,绝大多数为9 m;而在双车厢公交车中,大部分为12 m,也有少量车为15 m。综合考虑公交车、小汽车的车长及车与车间的安全距离,确定元胞尺寸为5 m,小汽车占1个元胞,公交车占2个元胞。

由于城市交通中干扰因素过多(如小区进出口、信号灯及斑马线、限速、机非干扰等),为确保安全行驶,驾驶员在驾驶车辆时往往比较保守。因此,确定公交车的最大车速为2个元胞(36 km/h),小汽车最大车速为3个元胞(54 km/h),即当车型type=1时, $\begin{matrix} v_{\max}^{car} \end{matrix}$ =3,当车型type=2时, $\begin{matrix} v_{\max}^{bus} \end{matrix}$ =2。在机动性方面,各类车辆差别较大,小轿车百公里加速时间在11~13 s,中型轿车一般在7~8 s,而跑车一般小于3.8 s。从百米加速考虑,其由静止加速行驶百米的时间从3 s到13 s不等,但大多数小汽车百米内行驶时间维持在9 s左右。同时,在实际的城市交通中,驾驶员通常不会将加速度提到车辆的极限值。通过观察发现,在城市交通中,小汽车在运行过程中加速比较缓和,与公交车差距较小,因此在模型中采用相同加速度 a=1。

1.1 跟驰规则

经典的NaSch模型确立了车辆更新的四条基本规则,然而,该规则模拟出的车辆跟驰行为与城市交通中的实际车辆跟驰行为有一定差距,主要表现在车速的确定和车辆慢启动行为上。VE模型在确定车辆速度时考虑了前车的速度,TT模型增加了慢启动规则,用以描述车辆在从零速度启动时的延误现象^{[ 14, 15, 16]}。本文综合了VE模型和TT模型的特点,同时增加了公交车因素,制定了新的跟驰规则。

计算允许最大速度:

$\begin{matrix} \begin{matrix} v'_{t + 1} \to \sqrt[]{2 (d_{t}^{n} + (v_{t}^{n + 1}) / 2)} (1) \\ 加速 : \\ \{\begin{matrix} v_{t + 1}^{n (car)} \to \max (v_{t}^{n (c ar)} + 1, v_{\max}^{car}, v'_{t + 1}) \\ v_{t + 1}^{n (bus)} \to \max (v_{t}^{n (bus)} + 1, v_{\max}^{bus}, v'_{t + 1}) \end{matrix} (2) \\ 减速 : \\ \{\begin{matrix} v_{t + 1}^{n (car)} \to \min (v_{t}^{n (car)} - 1,0, v'_{t + 1}) \\ v_{t + 1}^{n (bus)} \to \min (v_{t}^{n (bus)} - 1,0, v'_{t + 1}) \end{matrix} (3) \\ 慢启动 : flag = 1, v_{n} (p_{s}) \to 0 (4) \end{matrix} \end{matrix}$

随机慢化:以随机慢化概率 $\begin{matrix} p \end{matrix}$ 使

$\begin{matrix} \begin{matrix} v_{t + 1}^{n} \to \max (v_{t + 1}^{n} - 1,0) (5) \\ 位置更新 : x_{t + 1}^{n} = x_{t}^{n} + v_{t + 1}^{n} (6) \end{matrix} \end{matrix}$

规则中, $\begin{matrix} v'_{t + 1} 为根据前导车的速度以及前导车与本车间距得出的最大允许运行速度 (v'_{t + 1} 由 2 (v'_{t + 1})^{2} = d_{t}^{n} + 2 (v_{t}^{n + 1})^{2} 推导而来), d_{t}^{n} 为本车车头与前导车车尾间的距离, d_{t}^{n} = S - l, S 为车头间距, l 为车身长; v_{t + 1}^{n (car)} 表示在 t + 1 时刻小汽车的速度; v_{t}^{n (car)} 表示在 t 时刻小汽车的速度; v_{t + 1}^{n (bus)} \end{matrix}$ 表示在 $\begin{matrix} t + 1 \end{matrix}$ 时刻公交车的速度; $\begin{matrix} v_{\max}^{car} \end{matrix}$ 为小汽车的最大速度; $\begin{matrix} v_{\max}^{bus} \end{matrix}$ 为公交车的最大速度;flag表示本车加减速状态(0或1),当车辆受前导车的影响而减速时,flag=1,该车在下一时刻将以 $\begin{matrix} 1 - p_{s} 的概率向前行驶; rand () 是产生的随机数; p 为随机慢化概率; x_{t + 1}^{n} 为 t + 1 时刻车辆所在道路位置的坐标值; x_{t}^{n} 为 t \end{matrix}$ 时刻车辆所在道路位置的坐标值。

当驾驶员在确定下一时刻的速度时,不仅需要判断与前车的间距,同时还会判断前车的运行状态,这符合在高密度、低流速的城市交通流中驾驶员的心理。

1.2 换道规则

驾驶员的换道行为受换道条件和换道动机控制。换道条件为实际道路交通状况的反应,无法改变;换道动机受驾驶员自身特性的影响,包括年龄、性别、性格、情绪、驾龄、身体状况、目的地等。换道规则分为对称换道规则和非对称换道规则。由于我国规定超车道在左侧,因此采用左侧缺省的非对称换道规则。通过对174份SP调查问卷的统计发现,当有超车条件时,40.8%的驾驶员会选择从左侧超车,26.5%的驾驶员选择右侧超车,32.7%的驾驶员选择不超车。调查中还显示,当驾驶员准备超车时,如果发现目标车道后方有公交车,且本车道通畅,会有77.8%的驾驶员选择让行公交车;如果此时本车道拥挤,则有54.3%的驾驶员选择给公交车让行;如果此时本车道堵塞,则仅有37.0%的驾驶员选择让行公交车。

当路段上只有两条车道时,换道规则较为简单,即左侧车道车辆向右换道或右侧车道车辆向左换道。当车道数在3条以上时,中间车道的换道规则相对复杂,需判断左右两条车道的换道条件及换道动机。据此,本文研究制定了新的换道规则。

(1)左侧车道换道规则

左侧车道的换道规则下包含规则1和规则2。其中,规则1是满足换道条件和换道动机条件下的速度和位置更新规则;规则2是不满足换道条件或换道动机条件下的速度和位置更新规则。

当 $\begin{matrix} v_{t + 1}^{r} > v_{t + 1}^{s} 且 v_{t + 1}^{r} > v_{t}^{rb} + 1 时, 车辆以 p_{r} . p_{b} \end{matrix}$ 的概率换道(即满足换道动机)。换道规则规定,同时满足换道动机和换道条件时,当前车道(左侧车道)上的车辆向其右侧车道换道。使用规则1进行速度和位置的更新:

$\begin{matrix} \begin{matrix} v_{t + 1} = v_{t + 1}^{r} (7) \\ y_{t + 1} = y_{t} + 1, x_{t + 1} = x_{t} + v_{t + 1} (8) \end{matrix} \end{matrix}$

当不满足换道条件或换道动机时,车辆在当前车道向前行驶,采用规则2进行速度和位置更新:

$\begin{matrix} \begin{matrix} v_{t + 1} = v_{t + 1}^{s} (9) \\ y_{t + 1} = y_{t} + 1, x_{t + 1} = x_{t} + v_{t + 1} (10) \end{matrix} \end{matrix}$

$\begin{matrix} v_{t + 1}^{r} > v_{t + 1}^{s} 为换道条件, v_{t + 1}^{r} > v_{t}^{rb} + 1 为安全条件。 v_{t + 1}^{r} 指 t + 1 时刻车辆向右侧行驶能达到的最大速度; v_{t + 1}^{s} 指 t + 1 时刻当前车道车辆不换道行驶能达到的最大速度 (下文 v_{t + 1}^{l} 类同); y_{t + 1} 和 y_{t} 分别表示在 t + 1 时刻和 t 时刻车辆的横向坐标; x_{t + 1} 和 x_{t} 分别表示在 t + 1 时刻和 t 时刻车辆的径向坐标。 p_{r} . p_{b} 为换道动机, p_{r} 为驾驶员向右侧换道的意愿, p_{b} \end{matrix}$ 为公交车影响因子。

(2)右侧车道换道规则

右侧车道换道规则与左侧车道换道规则原理类似。当换道条件满足时,即 $\begin{matrix} v_{t + 1}^{l} > v_{t + 1}^{s} 且 v_{t + 1}^{l} > v_{t}^{lb} + 1, 车辆以 p_{l} . p_{b} \end{matrix}$ 的概率向其左侧的车道行驶。当满足向左侧位置的车道换道条件和换道动机时,采用规则1进行速度和位置更新:

$\begin{matrix} \begin{matrix} v_{t + 1} = {v^{l}}_{t + 1} (11) \\ y_{t + 1} = y_{t} - 1, x_{t + 1} = x_{t} + v_{t + 1} (12) \end{matrix} \end{matrix}$

当不满足换道条件或换道动机时,车辆向前行驶,采用规则2进行速度和位置更新:

$\begin{matrix} \begin{matrix} v_{t + 1} = {v^{s}}_{t + 1} (13) \\ y_{t + 1} = y_{t}, x_{t + 1} = x_{t} + v_{t + 1} (14) \end{matrix} \end{matrix}$

$\begin{matrix} v_{t + 1}^{l} 指 t + 1 时刻车辆如果向左侧行驶所能达到的最大速度; p_{l} \end{matrix}$ 为驾驶员向左侧换道的意愿。

(3)中间车道换道规则

与左侧车道换道规则和右侧车道换道规则相比,中间车道换道规则相对较为复杂。在判断换道条件和换道动机时,中间车道需将左、直、右三个方向的元素综合判断。

中间车道车辆向其右侧换道的条件为 $\begin{matrix} v_{t + 1}^{r} > v_{t + 1}^{s} 且 v_{t + 1}^{r} > v_{t + 1}^{l}, 安全条件为 v_{t + 1}^{r} > v_{t}^{rb} + 1, 当满足换道动机 p_{r} . p_{b} \end{matrix}$ 时,车辆向右侧换道,速度和位置更新使用规则1:

$\begin{matrix} \begin{matrix} v_{t + 1} = {v^{r}}_{t + 1} (15) \\ y_{t + 1} = y_{t} + 1, x_{t + 1} = x_{t} + v_{t + 1} (16) \end{matrix} \end{matrix}$

中间车道车辆向其左侧换道的条为 $\begin{matrix} v_{t + 1}^{l} > v_{t + 1}^{s} 且 v_{t + 1}^{l} > v_{t + 1}^{r}, 安全条件为 v_{t + 1}^{r} > v_{t}^{rb} + 1 。当满足换道动机 p_{l} . p_{b} \end{matrix}$ 时,车辆向右侧换道,速度和位置更新使用规则2:

$\begin{matrix} \begin{matrix} v_{t + 1} = {v^{l}}_{t + 1} (17) \\ y_{t + 1} = y_{t} - 1, x_{t + 1} = x_{t} + v_{t + 1} (18) \end{matrix} \end{matrix}$

当不满足向左、右两侧换道中任何一组条件时,车辆在原车道内向前行驶。速度和位置更新使用规则3:

$\begin{matrix} \begin{matrix} v_{t + 1} = {v^{s}}_{t + 1} (19) \\ y_{t + 1} = y_{t}, x_{t + 1} = x_{t} + v_{t + 1} (20) \end{matrix} \end{matrix}$

以上三条规则中参数都是对第 $\begin{matrix} n 辆车进行计算, 下标中省略了 n 字样。 p_{l} 、 p_{r} 和 p_{s} \end{matrix}$ 分别为向左换道意愿、向右换道意愿和不换道意愿,该意愿由年龄、性别等因素及非对称换道概率决定,依据1.2节中的调查结果,发现在满足换道条件下,向左换道概率较大,建议 $\begin{matrix} p_{l} 取 0.4, p_{r} 取 0.25, p_{s} \end{matrix}$ 取0.35;考虑到在大多数情况下,车流处于拥堵和通畅状态,因此依据1.2节中调查结果,认为大多数情况下有60%车辆在换道时会给公交车让行,因此,换道时有公交车的情况,只有40%车辆会选择换道,即公交车影响因子 $\begin{matrix} p_{b} 取 0.4; v_{t + 1} 为最终确定的 t + 1 时刻的车速; x 和 y \end{matrix}$ 分别为道路纵向和横向坐标值。

该模型中考虑了换道动机中的换道意愿和公交车影响因子,能够较好地反映出受公交车影响下的车辆换道行为。

2 模拟结果分析

在模拟过程中,设仿真时长为1000 s,仿真间隔时间为1 s,车道长度为 L=1000个元胞,车道数为3。车型分为小汽车和公交车,其中小汽车尺寸采用1个元胞,公交车采用2个元胞。小汽车的最大车速 $\begin{matrix} v_{\max}^{car} \end{matrix}$ =3,公交车的最大车速 $\begin{matrix} v_{\max}^{bus} \end{matrix}$ =2。其他基本参数设置具体如下:公交车比例为0.2,随机慢化概率 $\begin{matrix} p = 0.1, 慢启动概率 p_{s} = 0.75 。 \end{matrix}$

首先采用开放边界条件,在输入流量为800 veh/h的条件下分别模拟了单车道和三车道两种情况,得到模拟结果如图1及图2所示。图中黑色表示公交车,灰色表示小汽车。图1为单车道情况下(即不能换道)的时空图,流量为800 veh/h。图2(a)(b)(c)为三车道情况下的时空图,流量为800 veh/h,图1与图2(a)(b)(c)的其他参数完全相同。对比这4张图可以发现图1中有多处出现了停车排队,而图2(a)(b)(c)中尽管有车辆中途停下,但车辆排队现象不明显。这表明多车道的道路比单车道的道路稳定。因为在单车道条件下,道路中一旦出现停车,后车则必须停下等待,在慢启动的作用下,出现排队现象;而在多车道道路上,由于允许车辆换道,因此当前导车停下时,车辆可以选择换道绕行,从而使车流运行相对通畅。图2(d)(e)(f)为输入流量1000 veh/h条件下的时空图,其他参数与图2(a)(b)(c)相同。由于输入端流量上升,超出了道路的承载能力,使得部分路段出现亚稳态,而通过对时空图的分析发现,当出现排队时,各个车道均会受到影响。图2(d)(e)(f)中方框和圆圈内部分有明显相似性。这是由于当某个车道出现排队时,后边车辆会选择去相邻车道,干扰了相邻车道的车辆,当相邻车道也近似于饱和状态时,换道车辆会严重影响其正常运行。

	Figure Option View Download New Window
	图1 单车道的时空图Fig.1 Spatio-temporal of single lane

	Figure Option View Download New Window
	图2 换道规则下各车道的时空图Fig.2 Spatio-temporal of each lane under lane-change rules

对图2(a)(b)(c)中公交车比例及换道次数进行统计发现,在1000 s仿真内,三条车道公交车数分别为64、77和106,换道次数为6678、6243和8749。可以看出,公交车比例的升高会增加社会车辆的换道次数。

从图3中可以看出,由于公交车速度较低,会阻碍小汽车的前行。黑色线表示的公交车由于速度较低,导致其后边小汽车换道频繁(线条间断说明该车换道)。因此,公交车会影响车流整体的稳定性。由于公交车的最大尺寸为2个元胞,因此在流量为800 veh/h时,道路上车流速度较高,在多数情况下都能满足公交车运行的速度需求,图3中较少发现公交车有换道行为。

	Figure Option View Download New Window
	图3 图2(a)的局部放大Fig.3 Enlarged of part of fig.2(a)

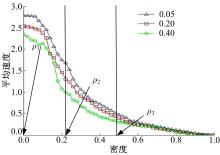
图4为3种公交车比例下的流密度。图中3条曲线分别表示公交车比例在0.05、0.20、0.40情况下的速密曲线。从这3条曲线可以分析出,车流速度随着公交车比例的上升而降低。在模拟中,公交车最大速度为2,小汽车最大速度为3,车流理想平均运行速度为3×小汽车比例+2×公交车比例,即公交车比例为0.05、0.20、0.40时,车流平均运行速度应该为2.95、2.8、2.6。当密度小于0.1时,由于车流基本处于自由流状态,因此平均运行速度较高,接近理想平均运行车速;当密度从 $\begin{matrix} ρ_{1} 降到 ρ_{2} 时, 车速急速下降, 在 ρ_{2} 点的车速只有在 ρ_{1} 点车速的 1 / 3 左右。当密度上升至 ρ_{3} \end{matrix}$ 时,3种公交车比例下的车流速度已基本无差距。因此,在高密度车流下,小汽车对公交车没有速度优势。

	Figure Option View Download New Window
	图4 3种公交车比例下的速密图Fig.4 Relationship between velocity and density under three different bus rate

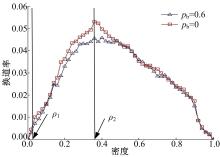
增加了公交车影响因子 p_b后,车辆换道行为受到其影响。通过RP调查发现,如果车辆准备超车时发现目标车道后边有公交车,6成左右的驾驶员选择让行公交车。图5为公交车比例为0.2、随机慢化概率 p=0.1、慢启动概率 p_s=0.75、公交影响因子 p_b分别取0和0.6时的模拟结果图。其中横坐标为密度,纵坐标为统计的换道率,方框线和三角线分别为 p_b取0和0.6时的换道率-密度曲线。

	Figure Option View Download New Window
	图5 换道率与车辆密度关系图Fig.5 Relationship between lane-change and density

分析图5发现,公交车影响因子的存在会降低换道率。然而,并非在所有密度段这一趋势都明显,当车流密度在 $\begin{matrix} ρ_{1} 和 ρ_{2} 之间时, 公交车影响因子对换道率影响较大, 而当 ρ < ρ_{1} 或 ρ > ρ_{2} 时, 道路分别处于通畅状态及堵塞状态, 公交车影响因子对换道率影响不显著。将图 5 与图 4 结合分析发现, 当 ρ < ρ_{1} 时道路通畅, 流速较高, 换道需求 (换道动机) 较小; 当 ρ > ρ_{2} 时, 车辆几乎无法动弹, 换道空间 (换道条件) 不足。密度在 ρ_{1} 和 ρ_{2} \end{matrix}$ 之间时,换道动机及换道条件兼备,因此换道率较高。但公交车影响因子降低了换道动机,使换道率也同时降低。

3 结束语

本文研究了公交车的存在对车辆换道行为的影响,提出了考虑公交车影响因子的换道规则,并对该规则进行模拟,分析公交车影响因子对道路车速、换道动机及换道行为的影响。通过模拟结果可以看出,公交车的存在使小汽车换道频率增加;当道路处于中低密度状态时,公交车降低了道路车流流速,但这一现象在高密度车流状态下消失;当换道动机中增加公交车影响因子后,在中低密度下的道路中,公交车影响因子会减少车辆换道概率。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	张发, 宣慧玉, 赵巧霞. 速度差异混合交通流稳态特性与过渡特性[J]. 系统工程学报, 2012, 27(2): 263-269. Zhang Fa, Xuan Hui-yu, Zhao Qiao-xia. Characteristics of mixed traffic flow with different velocities in steady state and transient process[J]. Journal of Systems Engineering, 2012, 27(2): 263-269. [本文引用:1] [CJCR: 0.817]
[2]	陈峻, 王涛, 李春燕, 等. 城市公交车与社会车辆混合流速度模型及交通运行状态分析[J]. 中国公路学报, 2012, 25(1): 128-140. Chen Jun, Wang Tao, Li Chun-yan, et al. Speed models of mixed traffic flow on bus car and vehicle and analysis of traffic running state[J]. China Journal of Highway and Transport, 2012, 25(1): 128-140. [本文引用:1] [CJCR: 2.996]
[3]	杨晓光, 阴炳成. 公共汽车交通专用道及其停靠站最佳布置方法[J]. 同济大学学报: 自然科学版, 2004, 32(7): 902-905. Yang Xiao-guang, Yin Bing-cheng. Optimal location of exclusive bus lane and bus stops[J]. Journal of Tongji University(Natural Science), 2004, 32(7): 902-905. [本文引用:1] [CJCR: 0.634]
[4]	贾斌, 李新刚, 姜锐, 等. 公交车站对交通流影响模拟分析[J]. 物理学报, 2009, 58(10): 6845-6850. Jia Bin, Li Xin-gang, Jiang Rui, et al. The influence of bus stop on the dynamics of traffic flow[J]. Acta Phys Sin, 2009, 58(10): 6845-6850. [本文引用:1] [JCR: 1.016] [CJCR: 1.691]
[5]	丁建勋, 黄海军. 考虑停靠站影响的公交运输系统模型[J]. 物理学报. 2010, 59(5): 3093-3098. Ding Jian-xun, Huang Hai-jun. A public transport system model with consideration of bus stop[J]. Acta Phys Sin, 2010, 59(5): 3093-3098. [本文引用:1] [JCR: 1.016] [CJCR: 1.691]
[6]	钱勇生, 汪海龙, 王春雷. 考虑公交港湾式停靠的多速混合城市交通流元胞自动机模型研究[J]. 物理学报, 2008, 57(4): 2115-2121. Qian Yong-sheng, Wang Hai-long, Wang Chun-lei. The study of a cellular automaton traffic flow model with public transit, harbor-shaped bus stop and mixed different-maximum-speed vehicles on single lane[J]. Acta Phys Sin, 2008, 57(4): 2115-2121. [本文引用:1] [JCR: 1.016] [CJCR: 1.691]
[7]	孙有信, 汪海龙, 钱勇生, 等. 周期边界下公交影响的双车道多速元胞自动机模型[J]. 系统工程理论与实践, 2008, 28(4): 172-176. Sun You-xin, Wang Hai-long, Qian Yong-sheng, et al. Mixed multi-speed vehicles on two-lane cellular automaton model under public transit influence with period boundary condition[J]. Systems Engineering-Theory&Practice, 2008, 28(4): 172-176. [本文引用:1]
[8]	钱勇生, 汪海龙. 考虑公交车辆影响的城市交通流元胞自动机模型[J]. 系统仿真学报, 2007, 19(14): 3358-3360. Qian Yong-sheng, Wang Hai-long. New cellular automaton city tramc model considering public transport vehicles affect with mixed traffic flow[J]. Journal of System Simulation, 2007, 19(14): 3358-3360. [本文引用:1] [CJCR: 0.914]
[9]	张建鹏, 廖唱, 杨远舟, 等. BRT信号优先的元胞自动机仿真研究[J]. 交通运输系统工程与信息, 2011, 11(6): 61-67. Zhang Jian-peng, Liao Chang, Yang Yuan-zhou, et al. Study on the signal priority of BRT by the simulations based on the cellular automata model[J]. Journal of Transportation Systems Engineering and Information Technology, 2011, 11(6): 61-67. [本文引用:1] [CJCR: 0.4688]
[10]	Nagel K, Schreckenberg M. A cellular automaton model for freeway traffic[J]. Journal de Physique I, 1992, 2(12): 2221-2229. [本文引用:1]
[11]	邝华, 孔令江, 刘慕仁. 多速混合车辆单车道元胞自动机交通流模型的研究[J]. 物理学报, 2004, 53(9): 2894-2898. Kuang Hua, Kong Ling-jiang, Liu Mu-ren. The study of a cellular automaton traffic flow model with mixed different maximum speed vehicles on single lane[J]. Acta Phys Sin, 2004, 53(9): 2894-2898. [本文引用:1] [JCR: 1.016] [CJCR: 1.691]
[12]	郑容森, 谭惠丽, 孔令江, 等. 双车道多速车辆混合交通流元胞自动机模型的研究[J]. 物理学报, 2005, 54(8): 3516-3522. Zheng Rong-sen, Tan Hui-li, Kong Ling-jiang, et al. A cellular automaton model for mixing traffic in two-lane system[J]. Acta Phys Sin, 2005, 54(8): 3516-3522. [本文引用:1] [JCR: 1.016] [CJCR: 1.691]
[13]	Jia B, Gao Z Y, Li K P, et al. Models and Simulations of Traffic System Based on the Theory of Cellular Automaton[M]. Beijing: Science Press, 2007. [本文引用:1]
[14]	Kerner B S. Traffic flow: experiment and theory[C]∥Traffic and Granular Flow 97, Heidelberg, 1998: 239-267. [本文引用:1]
[15]	Schadschneider A, Schreckenberg M. Traffic flow models with 'slow-to-start' rules[J]. Annalen der Physik, 1997, 509(7): 541-551. [本文引用:1]
[16]	Wagner P, Nagel K, Wolf D E. Realistic multi-lane traffic rules for cellular automata[J]. Physica A: Statistical Mechanics and its Applications, 1997, 234: 687-698. [本文引用:1] [JCR: 1.676]

2012

0.0

0.817

... 由于公交车运行速度通常比社会车辆低,有公交车的交通流常表现出不同的稳态与亚稳态特性^[1] ...

2012

0.0

2.996

. 2012, 25(1):128-140

Speed models of mixed traffic flow on bus car and vehicle and analysis of traffic running state

1. School of Transportation, Southeast University, Nanjing 210096, Jiangsu, China;2. School of Architecture and Transportation, Guilin University of Electronic Technology, Guilin 541004, Guangxi, China; 3. School of Economics and Management, Chang'an University, Xi'an 710064, Shaanxi, China

In order to analyze the mixed traffic running state of bus-car and vehicle accurately, based on applicability analysis of the basic road speed model, authors introduced different traffic parameters, such as bus-car volume, vehicle volume and ratio of bus-car and put forward running speed model of mixed vehicle. By using Metrocount 5600 pneumatic-tube vehicle type system, authors collected the empirical data from three-lanes one-way and two-lanes one-way road section by traffic test investigation and calibrated the parameters of modified speed models. Furthermore, velocity difference models with two vehicle types were set up to describe the mixed traffic flow performance. Evaluation methods of three kinds of traffic running states of mixed traffic flow were put forward. Results show that different ratios of bus-car have the significant impact on the vehicle speed under the same volume of traffic flow in three ranges. With the increment of road saturation, the velocity difference between bus-car and vehicle varies from stable to quick approaching and to zero. Consideration of ratio variation of bus-car in the composition of vehicle traffic flow can refine different discriminations of traffic smooth state, congestion production state and the congestion state judgement.

为了精确解析城市公交车和社会车辆混合运行的状态,在基本路段车速模型适用性分析的基础上,引入公交车流量、社会车辆流量、公交车比例等参数,建立了改进的混合机动车运行速度模型,分别选取单向二车道和单向三车道路段进行交通试验调查,采用Metrocount 5600气压管式车辆分型系统进行数据采集并用于改进模型的参数标定,并分别建立了2种车型的速度差模型,提出了路段混合车流3种不同交通运行状态的评价方法。研究结果表明:同等车流量情况下,不同公交车比例对社会车辆速度的影响表现为3个显著的变化区间;随着路段饱和度的增加,社会车辆和公交车之间的速度差呈现出从几乎不变、快速缩小到接近于零3个较为明显的运行状态;考虑车流组成中公交车比例的变化可以细化路段车流畅通状态、拥堵形成状态以及拥堵状态的判别。

... 因此,通过仿真建模的方式对城市公交车与社会车辆混行车流进行分析是了解混合交通流运行状态的一种有效手段^[2] ...

2004

0.0

0.634

... 当前,多数学者把关注点放在公交车停靠站对交通流的影响^[3,4,5,6]以及包含公交专用道的车流行为研究上^[7,8,9],但对混合车流中公交车会如何影响车流中车辆换道行为的研究较少 ...

2009

1.016

1.691

. 2009, 58(10):6845-6850

The influence of bus stop on the dynamics of traffic flow

(1)北京交通大学交通运输学院,城市交通复杂系统理论与技术教育部重点实验室，北京 100044; (2)中国科技大学工程科学学院，合肥 230026

The impact of bus stop on the dynamics of traffic flow is studied by a cellular automata model. Two types of bus stops, non-harbor shaped and harbor shaped, are considered. The properties of traffic flow are investigated by analyzing the fundamental diagram and the spatial-temporal diagram. The influences of bus ratio and length of bus stop are analyzed in detail. The simulation results show that the non-harbor shaped bus stop has more influence on the traffic flow, and the flux cannot be effectively increased by extending the bus stop length; the harbor shaped bus stop has less influence on the traffic flow and the flux can be improved by extending the bus stop length.

采用元胞自动机模型对城市道路中公交车站影响下的交通流特性进行模拟分析.研究了非港湾式车站和港湾式车站两种设置方式下交通流特性，对公交车比例和公交车站长度的影响进行了分析.模拟结果显示非港湾式车站对交通流的影响较大，通过增加车站长度并不能有效地提高系统流量；港湾式车站对交通流的影响较小，通过增加车站长度可以较大程度地增加系统流量.

2010

1.016

1.691

. 2010, 59(5):3093-3098

A public transport system model with consideration of bus stop

北京航空航天大学经济管理学院，北京 100191

Clustering of bus flow easily occurs due to the influence of bus stop. A new cell automaton model which considers the length and distribution of bus stations is proposed in this paper. Numerical simulation shows that the model can explicitly depict the space-time trajectories of bus movement along a bus line, reproduce the clustering phenomenon of bus flow, and quantitatively evaluate the impact of bus station distribution on bus average speed. The study provides insight on formation mechanism of clustering and may contribute to the optimization of locating bus stations.

受停靠站影响，公共交通系统运行过程中容易产生集簇现象.本文细致地考虑了公交停靠站长度和停靠站在线路上的分布情况，构建了一个新的公交运输系统元胞自动机模型.数值模拟结果表明，在引入停靠站长度和停靠站分布两种因素后，模型在微观层面上更清晰地刻画了车辆在公交线路上的时空分布，再现了公交运行中的集簇现象，定量地评价了停靠站分布对车辆平均速度的影响.本研究对进一步认识集簇现象的形成机理和优化停靠站设计具有指导意义.

2008

1.016

1.691

. 2008, 57(4):2115-2121

The study of a cellular automaton traffic flow model with public transit, harbor-shaped bus stop and mixed different-maximum-speed vehicles on single lane

兰州交通大学交通运输学院，兰州 730070

Based on the Nagel-Schreckenberg models of traffic flow， a cellular automaton traffic model with different-maximum-speed vehicles mixed on single lane is proposed， which considers public transit and harbor-shaped bus stop. The influence of deceleration probability， the density of vehicles， the average stop time of public transit vehicles， the proportion of public transit vehicles occupied in the mixed vehicles and the bus stop spacing on mixed traffic flow are analyzed by computer simulation. The models traffic flow characters are presented and analyzed.

在Nagel-Schreckenberg提出的元胞自动机模型基础上，建立了考虑公交车辆和港湾式公交停靠站的多速混合车辆单车道城市交通流元胞自动机模型.通过计算机模拟，给出了随机减速概率、混合车流密度、公交车辆平均停靠时间、公交车辆占有率和港湾式公交车站间距对混合车流速度和流量的影响图.对混合车流的特性进行了分析和讨论.

2008

0.0

2007

0.0

0.914

2011

0.0

0.4688

1992

0.0

... Nagel和Schreckenberg于1992年提出的NaSch模型是最著名的交通流元胞自动机模型^[10] ...

2004

1.016

1.691

. 2004, 53(9):2894-2898

The study of a cellular automaton traffic flow model with mixed different maximum speed vehicles on single lane

广西师范大学物理与信息工程学院，桂林\ 541004

Based on the NS models of traffic flow, a cellular automaton traffic mo del with different-maximum-speed vehicles mixed on single lane is proposed. We p resent the fundamental diagrams of traffic flow under different parameters by us ing computer numerical simulation. The model's traffic flow characters are prese nted and analyzed.

在交通流NS模型的基础上，建立了多速混合车辆单车道元胞自动机交通流模型，通过计算机数值模拟，得到了混合车辆在不同参数下交通流模型的基本图，并对混合交通的特性进行了分析和讨论.

... 为描述更丰富的车辆运行行为,学者们在NaSch模型的基础上提出了大量改进模型^[11,12,13] ...

2005

1.016

1.691

. 2005, 54(8):3516-3522

A cellular automaton model for mixing traffic in two-lane system

(1)广西师范大学物理与信息工程学院,桂林 541004; (2)玉林师范学院物理与信息科学系,玉林 537000

Based on the Nagel-Schrekenberg(NS) model,we present a mixing traffic flow model for a two-lane traffic system. In this model,the stochastic noise P in NS model is replaced by accelerating probability P a and braking probabil ity P d . The fundamental diagrams of the mixing traffic under differen t conditi ons are given by the numerical simulations. We found that the lane-changing prob ability,the mixing rate and acceleration, the braking probability have a great i nfluence on the mixing traffic flow. The slow cars have a decisive action on the mixing traffic.

把NaSch模型的刹车概率分开为独立的加速和减速概率，引入转道规则，建立了双车道多速车辆的混合交通流模型.通过计算机数值模拟，得出了不同参数下混合交通的速度和流量与密度关系的基本图.结果表明，转道概率、混合比例和加减速概率对混合交通都有重要的影响，慢车的特性对混合交通起着决定性的作用.

... 为描述更丰富的车辆运行行为,学者们在NaSch模型的基础上提出了大量改进模型^[11,12,13] ...

2007

0.0

... 为描述更丰富的车辆运行行为,学者们在NaSch模型的基础上提出了大量改进模型^[11,12,13] ...

1998

0.0

... VE模型在确定车辆速度时考虑了前车的速度,TT模型增加了慢启动规则,用以描述车辆在从零速度启动时的延误现象^[14,15,16] ...

1997

0.0

. 1997, 509(7):541-551

Traffic flow models with ‘slow-to-start’ rules

Andreas Schadschneider 1 andMichael Schreckenberg 2

1 Institut für Theoretische Physik, Universität zu Köln, D-50937 Köln, Germany 2 Theoretische Physik/FB 10, Gerhard-Mercator-Universität Duisburg, D-47048 Duisburg, Germany

> We investigate two models for traffic flow with modified acceleration (‘slow-to-start’) rules. Even in the simplest case v max = 1 these rules break the ‘particle-hole’ symmetry of the model. We determine the fundamental diagram (flow-density relationship) using the so-called car-oriented mean-field approach (COMF) which yields the exact solution of the basic model with v max = 1. Here we find that this is no longer true for the models with modified acceleration rules, but the results are still in good agreement with simulations. We also compare the effects of the two different slow-to-start rules and discuss their relevance for real traffic. In addition, in one of these models we find a new phase transition to a completely jammed state.

... VE模型在确定车辆速度时考虑了前车的速度,TT模型增加了慢启动规则,用以描述车辆在从零速度启动时的延误现象^[14,15,16] ...

1997

1.676

0.0

. 1997, 234:null-null

Realistic multi-lane traffic rules for cellular automata

... VE模型在确定车辆速度时考虑了前车的速度,TT模型增加了慢启动规则,用以描述车辆在从零速度启动时的延误现象^[14,15,16] ...