多段式自动泊车路径规划及其关键技术

引用本文

钱立军, 胡伟龙, 刘庆, 吴冰. 多段式自动泊车路径规划及其关键技术.吉林大学学报:工学版, 2016, 46(3): 785-791
QIAN Li-jun, HU Wei-long, LIU Qing, WU Bing. Multiple segment method for automatic parking path planning and its key technology. Journal of Jilin University Engineering and Technology Edition, 2016, 46(3): 785-791 复制到剪切板

Permissions

多段式自动泊车路径规划及其关键技术

钱立军¹, 胡伟龙^1,², 刘庆³, 吴冰¹

1.合肥工业大学机械与汽车工程学院,合肥 230009

2.安徽江淮汽车集团有限公司博士后科研工作站,合肥 230601

3.泰安航天特种车有限公司项目管理部,泰安 271000

作者简介:钱立军(1962-),男,教授,博士生导师.研究方向:车辆电子,车辆控制.E-mail:13635601581@139.com

基金:工信部电子信息产业发展基金项目(工信部财[2009]453号)

摘要

为了设计一种在泊车过程中较连贯且计算量少的泊车路径,提出了泊车过程中方向盘匀速转动的策略。首先推导出车辆低速行驶时,匀速转动方向盘时后轴中心点的运动轨迹。然后将泊车过程分为5个阶段,按照避障条件求解出最优化的路径参数。设计了基于PID闭环反馈的车速控制系统,并通过试验得出实际车速对预期车速的跟踪效果良好的结论。通过泊车控制器模拟出EPS控制器需要的转矩传感器信号,设计了方向盘转速控制系统,利用系统辨识的方法得到转矩与转速的关系,并通过试验发现辨识得到的转矩与实际转矩的拟合度在96%以上。通过比较五段式泊车和两段式泊车过程中的车速、转角、油门控制量、刹车控制量随时间的变化关系,可以看出五段式泊车过程更加连贯。

关键词: 交通运输系统工程; 自动泊车; 路径规划; 车速控制; 方向盘转速控制

中图分类号:U463.67 文献标志码:A 文章编号:1671-5497(2016)03-0785-07

Multiple segment method for automatic parking path planning and its key technology

QIAN Li-jun¹, HU Wei-long^1,², LIU Qing³, WU Bing¹

1.School of Mechanical and Automotive Engineering, Hefei University of Technology, Hefei 230009,China

2.Postdoctoral Work Station, Anhui Jianghuai Automobile Co., Ltd., Hefei 230601,China

3.Project Management Department, Taian Aerospace Special Vehicle Co. Ltd. Taian 271000,China

Abstract

A strategy to turn the steering wheel uniformly while parking is put forward to design a parking path with more consistency and fewer calculations. First, the trajectory of the center point on rear axle is deduced while the vehicle is driven at low speed and the steering wheel is turned uniformly. Second, the parking process is divided into five stages and the parameters of the optimized path are obtained according to obstacle avoidance. Third, the vehicle speed control system based on the PID closed-loop feedback theory is designed, and experiments show that the real speed matches the expected speed. Fourth, the signal of the torque sensor needed by EPS controller is simulated by parking controller; then the steering wheel rotational speed control system is designed, and relationship between the torque and rotational speed is obtained by system identification. Experiments show that the degree of fitting between torques given by system identification and real torques is above 96%. Finally, the change of vehicle speed, rotating angle of the steering wheel, accelerator and brake of two segment parking and five segment parking are obtained. Comparison of two segment parking and five segment parking shows that five segment parking has higher consistency.

Keyword: engineering of communication and transportation system; automatic parking; path planning; vehicle speed control; steering wheel rotational speed control

Show Figures

自动泊车系统能够降低驾驶员的操作负担, 减小泊车事故发生率。目前, 泊车外部环境建模技术已经比较成熟, 主要是基于超声波雷达测距和双目成像原理建立泊车外部环境^{[1, 2]}。研究热点主要集中在泊车路径的规划, 主要有3种路径规划方式:文献^{[3, 4, 5]}采用模糊控制的策略, 提出了来回多段移动式的泊车路径规划方法; 文献^{[6, 7, 8]}提出了基于B样条曲线、五次多项式曲线、贝塞尔曲线等曲率连续的泊车路径规划方法; 文献^[9]提出了由圆弧和直线组成的曲率不连续的泊车路径规划方法。

基于模糊控制策略及曲率连续的路径规划方法, 泊车过程中不需要停车转动方向盘, 但是计算量较大; 基于曲率不连续的路径规划, 特别是两段式泊车路径规划方法计算量小, 但是泊车连贯性低^[10]。文献^[11]提出了采用缓和曲线线型进行路径规划, 将泊车路径分为七段, 但未做深入研究。本文在此基础上提出采用曲率连续的五段曲线构成泊车路径, 假设方向盘匀速转动且车辆后退速度恒定, 并对车速和方向盘转速进行了跟踪控制。

1 车辆低速运动轨迹

因为车辆后轮与车身运动方向一致, 后轮轨迹在车体运动过程中能完全体现车体的运动特征, 所以用后轮轴线中心点的轨迹来代表泊车轨迹。根据文献^[12], 车辆在低速运动时, 不计车轮的侧向滑动, 车辆后轴中心点的瞬时半径R=lcotψ , 其中l为汽车的轴距; ψ 为车辆瞬时Ackerman转角。

下面来讨论方向盘匀速转动时车辆后轴中心点的轨迹。由于电机的启动加速时间在毫秒级别, 此时车辆走过的距离也在厘米级别, 所以可以不考虑电机的启动加速时间。

方向盘以角速度ω 匀速转动, 即ψ =kω t, 其中k为Ackerman转角与方向盘转角之比(本文取1/15), 定义车辆后轴中心点的坐标为( $\begin{matrix} x, y \end{matrix}$ ), 根据车辆后轴中心点的瞬时半径和速度 $\begin{matrix} v \end{matrix}$ 有:

$\begin{matrix} \{\begin{matrix} x^{2} + y^{2} = {(lcotkωt)}^{2} \\ {(Δ x)}^{2} + {(Δ y)}^{2} = {(vΔt)}^{2} \end{matrix} \end{matrix}$ (1)

于是车辆后轴中心点轨迹的方程为:

$\begin{matrix} \{\begin{matrix} {(y')}^{2} + \frac{2 kωyy'}{lsin 2 kωt} + \frac{y^{2} ta n^{2} kωt}{l^{2}} + \\ \frac{4 k^{2} ω^{2} - v^{2} si n^{4} kωt}{si n^{4} kωt} = 0 \\ x' = dx / dt \\ y' = dy / dt \end{matrix} \end{matrix}$ (2)

可以在Matlab中调用ode45求解方程(2), 带入初始条件:

y=dsolve(‘ Dy=odefun1’ , ‘ y(0)=0, Dy(0)=15’ , ‘ t’ )

x=dsolve(‘ Dy=odefun2’ , ‘ y(0)=0, Dy(0)=15’ , ‘ t’ )

解得y=F₁(t), x=F₂(t)以及该轨迹在t时刻与x轴的夹角ψ (t):ψ (t)=F'₁(t)/F'₂(t)。

2 泊车运动的轨迹规划

2.1 泊车路径规划

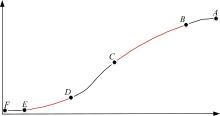
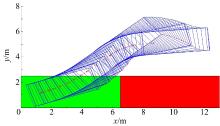
如图1所示, 开始泊车时刻, 车辆后轴中心点所在位置定义为A点, 车辆的初始姿态角为θ , 开始时车辆轮胎状态为回正状态。

	Figure Option View Download New Window
	图1 泊车过程路线示意图Fig.1 Diagrammatic sketch of parking route

泊车第1阶段, 泊车控制器控制车辆以速度 $\begin{matrix} v \end{matrix}$ 后退; 同时泊车控制器控制EPS, 使得方向盘以转动角速度 $\begin{matrix} ω \end{matrix}$ 匀速向左转动, 直到前转向轮达到左侧最大转角。此时车辆后轴中心点的轨迹为第1节中的轨迹。当方向盘转到车辆转向盘最大输入角34.455° 时, 车辆后轴中心点所在位置记作B点, 耗时记作t₁。

泊车第2阶段, 车辆以速度 $\begin{matrix} v \end{matrix}$ 后退, 同时泊车控制器控制EPS, 使得方向盘保持左侧最大转角不变, 此时车辆做类似圆周运动, 圆半径为车辆最小转弯半径R_min, 当类似圆周运动的圆心角为m时, 第2阶段结束。车辆后轴中心点所在位置记作C点, 耗时记作t₂。

泊车第3阶段, 车辆以速度 $\begin{matrix} v \end{matrix}$ 后退, 同时泊车控制器控制EPS, 使得方向盘以转动角速度 $\begin{matrix} ω \end{matrix}$ 匀速向右转动, 直到前转向轮达到右侧最大转角。当方向盘转到车辆转向盘最大转角时, 车辆后轴中心点所在位置记作D点, 耗时为2t₁。

泊车第4阶段, 车辆以速度 $\begin{matrix} v \end{matrix}$ 后退, 同时泊车控制器控制EPS, 使得方向盘保持右侧最大转角不变, 此时车辆做类似圆周运动, 圆半径为车辆最小转弯半径R_min, 当类似圆周运动的圆心角为n时, 第4阶段结束。车辆后轴中心点所在位置记作E点, 耗时记作t₃。

泊车第5阶段, 车辆以速度 $\begin{matrix} v \end{matrix}$ 后退, 同时泊车控制器控制EPS, 使得方向盘以转动角速度 $\begin{matrix} ω \end{matrix}$ 匀速向左转动, 直到前转向轮回正, 第5阶段结束。车辆后轴中心点所在位置记作 $\begin{matrix} F 点, 耗时 t_{1} 。 \end{matrix}$

以上泊车过程中车身姿态角随时间变化, 记车身姿态角为 $\begin{matrix} θ (t), \end{matrix}$ 根据几何关系有:

$\begin{matrix} \begin{matrix} θ (t) = \\ \{\begin{matrix} θ + ψ (t), t \in (0, t_{1}] \\ θ + ψ (t_{1}) + (t - t_{1}) v / R_{\min}, \\ t \in (t_{1}, t_{1} + t_{2}] \\ θ + ψ (t_{1}) + m + ψ (t - t_{1} - t_{2}), \\ t \in (t_{1} + t_{2}, 2 t_{1} + t_{2}] \\ θ + 2 ψ (t_{1}) + m + ψ (t - 2 t_{1} - t_{2}), \\ t \in (2 t_{1} + t_{2}, 3 t_{1} + t_{2}] \\ θ + ψ (t_{1}) + m - (t - 3 t_{1} - t_{2}) v / R_{\min}, \\ t \in (3 t_{1} + t_{2}, 3 t_{1} + t_{2} + t_{3}] \\ θ + ψ (t_{1}) + m - n - (t - 3 t_{1} - t_{2} - t_{3}) v / R_{\min}, \\ t \in (3 t_{1} + t_{2} + t_{3}, 4 t_{1} + t_{2} + t_{3}] \end{matrix} \end{matrix} \end{matrix}$ (3)

式中: $\begin{matrix} t_{1} = 34.455 / (kω); t_{2} = m R_{\min} / v; t_{3} = n R_{\min} / v 。 \end{matrix}$

以A点为坐标原点, 在泊车过程中车辆后轴中心点的坐标也随着时间不停变化, 记后轴中心点的X轴坐标为x_o(t)、Y轴坐标为y_o(t), 则根据几何关系有:

$x_{o} (t) = \{\begin{matrix} - [F_{2} (t) cosθ - F_{1} (t) sinθ], t \in (0, t_{1}] \\ x_{o} (t_{1}) - [R_{\min} sinθ (t) - R_{\min} sinθ (t_{1})], \\ t \in (t_{1}, t_{1} + t_{2}] \\ x_{o} (t_{1} + t_{2}) - {[F_{1} (t - t_{1} - t_{2}) + F_{2} (t_{1}) - \\ F_{1} (t_{1})] cosθ (t) + [F_{2} (t - t_{1} - t_{2}) + F_{1} (t_{1}) - \\ F_{2} (t_{1})] cosθ (t_{1} + t_{2})}, \\ t \in (t_{1} + t_{2}, 3 t_{1} + t_{2}] \\ x_{o} (3 t_{1} + t_{2}) - [R_{\min} sinθ (t) - R_{\min} sinθ (3 t_{1} + t_{2})], \\ t \in (3 t_{1} + t_{2}, 3 t_{1} + t_{2} + t_{3}] \\ x_{o} (3 t_{1} + t_{2} + t_{3}) - {[F_{1} (t - t_{1} - t_{2}) + F_{2} (t_{1}) - \\ F_{1} (t_{1})] cosθ (t) + [F_{2} (t - t_{1} - t_{2}) + F_{1} (t_{1}) - \\ F_{2} (t_{1})] cosθ (3 t_{1} + t_{2} + t_{3})}, \\ t \in (3 t_{1} + t_{2} + t_{3}, 4 t_{1} + t_{2} + t_{3}] \end{matrix}$ (4)

$y_{o} (t) = \{\begin{matrix} - [F_{2} (t) sinθ + F_{1} (t) cosθ], t \in (0, t_{1}] \\ y_{o} (t_{1}) - [R_{\min} cosθ (t_{1}) - R_{\min} cosθ (t)], \\ t \in (t_{1}, t_{1} + t_{2}] \\ y_{o} (t_{1} + t_{2}) - {[F_{1} (t_{1}) + F_{2} (t_{1}) - \\ F_{2} (t - t_{1} - t_{2})] sinθ (t) + [F_{1} (t_{1}) + F_{2} (t_{1}) - \\ F_{1} (t - t_{1} - t_{2})] sinθ (t_{1} + t_{2})}, \\ t \in (t_{1} + t_{2}, 3 t_{1} + t_{2}] \\ y_{o} (3 t_{1} + t_{2}) - [R_{\min} cosθ (3 t_{1} + t_{2}) - R_{\min} cosθ (t)], \\ t \in (3 t_{1} + t_{2}, 3 t_{1} + t_{2} + t_{3}] \\ y_{o} (3 t_{1} + t_{2} + t_{3}) - {[F_{1} (t_{1}) + F_{2} (t_{1}) - \\ F_{2} (t - t_{1} - t_{2})] sinθ (t) + [F_{1} (t_{1}) + F_{2} (t_{1}) - \\ F_{1} (t - t_{1} - t_{2})] sinθ (3 t_{1} + t_{2} + t_{3})}, \\ t \in (3 t_{1} + t_{2}, 4 t_{1} + t_{2} + t_{3}] \end{matrix}$ (5)

在每一个阶段有车辆的前右顶点P_fr、前左顶点P_fl、后右顶点P_rr、后左顶点P_rl的坐标分别为:(x_fr, y_fr)、(x_fl, y_fl)、(x_rr, y_rr)、(x_rl, y_rl), 记车辆前悬为w_f; 车辆后悬为w_r; 车辆宽度为l_v, 根据几何关系有:

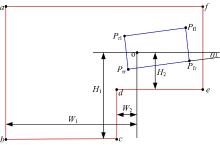
$\begin{matrix} \{\begin{matrix} x_{fr} (t) = x_{o} (t) - [ω_{f} cosθ (t) + l_{v} sinθ (t \frac{)}{2}] \\ y_{fr} (t) = y_{o} (t) - [ω_{f} sinθ (t) - l_{v} cosθ (t \frac{)}{2}] \\ x_{fl} (t) = x_{o} (t) - [ω_{f} cosθ (t) - l_{v} sinθ (t \frac{)}{2}] \\ y_{fl} (t) = y_{o} (t) - [ω_{f} sinθ (t) + l_{v} cosθ (t \frac{)}{2}] \\ x_{rr} (t) = x_{o} (t) + [ω_{r} cosθ (t) - l_{v} sinθ (t \frac{)}{2}] \\ y_{rr} (t) = y_{o} (t) + [ω_{r} sinθ (t) + l_{v} cosθ (t \frac{)}{2}] \\ x_{rl} (t) = x_{o} (t) + [ω_{r} cosθ (t) + l_{v} sinθ (t \frac{)}{2}] \\ y_{rl} (t) = y_{o} (t) + [ω_{r} sinθ (t) - l_{v} cosθ (t \frac{)}{2}] \end{matrix} \end{matrix}$ (6)

2.2 路径参数的确定

记A点到车位左侧距离为W₁; A点到车位右侧距离为W₂; A点到车位上部距离为H₁; A点到车位下部距离为H₂ 。于是可以用点a~f组成的空间作为泊车过程中的避障空间(见图2), 即只要车辆的4个顶点始终在避障空间内, 就不会发生碰撞。点a~f坐标分别为 $a (- W_{1}, 3.5); b (- W_{1}, H_{1}); c (- W, H_{1}); d (- W_{2}, H_{2}); e (3, - H_{1}); f (3, 3.5)$ 。

	Figure Option View Download New Window
	图2 泊车过程中的避障空间Fig.2 Obstacle avoidance space in process of parking

在泊车结束后的 $\begin{matrix} f \end{matrix}$ 点处, 车身姿态角为0, 车辆前轮处于回正状态, 于是有:

$θ (t_{f}) = θ (4 t_{1} + t_{2} + t_{3}) = θ + m - n = 0$ (7)

同时根据车辆后轴中心点坐标变化有:

$\begin{matrix} \{\begin{matrix} x_{o} (t_{f}) = x_{o} (4 t_{1} + t_{2} + t_{3}) = - W_{1} + w_{r} \\ y_{o} (t_{f}) = y_{o} (4 t_{1} + t_{2} + t_{3}) = - H_{1} + l_{v} / 2 \end{matrix} \end{matrix}$ (8)

通过联立式(4)(5)(7)(8)可以得到方向盘转动的角速度ω 与第一次圆周运动的圆心角m、车速v之间的关系为:

$\begin{matrix} \{\begin{matrix} F_{3} (m, ω, v, R_{\min}, θ, W_{1}) = 0 \\ F_{4} (m, ω, v, R_{\min}, θ, H_{1}) = 0 \end{matrix} \end{matrix}$ (9)

从式(9)可以看出: $\begin{matrix} ω 、 m 、 v \end{matrix}$ 是未知参数, 其解不是唯一的。

根据简化, 车辆的4个顶点始终在避障空间内只需要满足以下条件:

$\begin{matrix} \{\begin{matrix} y_{fl} (t) < 3.5 \\ x_{fr} (τ) = - W_{2}, y_{fr} (τ) > - H_{2} \\ x_{rr} (t) > - W_{1}, x_{rl} (t) > - W_{1} \\ y_{rr} (t) > - H_{1}, y_{rl} (t) > - H_{1} \\ τ \in (0, 4 t_{1} + t_{2} + t_{3}], t \in (0, 4 t_{1} + t_{2} + t_{3}] \end{matrix} \end{matrix}$ (10)

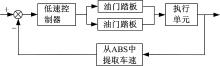
在Matlab中让 $\begin{matrix} m \end{matrix}$ 在(25° , 60° ]内以0.5° 的梯度变化, 得到一系列的解, 将解代入不等式(10)中剔除不满足避障条件的解, 得到部分最终可行解。再对这部分解求车速 $\begin{matrix} v \end{matrix}$ 的积分, 取积分最小的解为最终的合适解。

3 车速和方向盘转角的控制

本文设计的低速控制系统结构如图3所示。该系统以期望车速和实测车速间的偏差最小为控制目标, 使用PID控制算法确定控制量, 即油门的开合和制动踏板的切换, 以实现车速的增、减变化。

	Figure Option View Download New Window
	图3 低速控制系统结构图Fig.3 Structure chart of low speed control system

期望车速与实测车速间的偏差为:v_d=v_p-v_r, 其中v_d为期望车速与实测车速间的偏差, v_p为期望车速; v_r为ABS实测车速。设控制量为u, 根据PID理论有:

$\begin{matrix} u = K_{P} v_{d} + K_{D} {\overset{\cdot}{v}}_{d} + K_{I} \int_{0}^{t} v_{d} dτ \end{matrix}$

式中:K_P、K_D、K_I分别为控制器的比例、微分和积分系数; u大于0, 表示车辆需要进行加速操作, u小于0, 表示车辆需要减速操作。

车辆的加、减速操作对应的油门的开合和制动踏板的切换关系在文献^{[13, 14, 15]}中有具体阐述。

文献^[16]中, 方向盘转速的控制是通过在方向盘上安装转向电机实现, 或者在EPS系统中加装方向盘转角传感器通过闭环调节来达到预期的转速, 这些方法在试验中可行, 大规模的生产中受到安装和成本的制约。

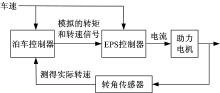
设计转向控制系统的结构如图4所示, EPS只接受车速和转矩传感器的信号。泊车控制器根据方向盘实际转速与期望的转速之差、车速产生模拟的转矩和转速信号; EPS控制器根据模拟的转矩和转速信号产生助力电机所需要的电流, 从而达到闭环控制转速的目的。

	Figure Option View Download New Window
	图4 转速控制系统结构图Fig.4 Structure chart of revolving speed control system

这套方向盘转角控制方法的优势在于充分利用现有EPS系统的硬件结构, 不改变EPS系统的原有程序, 只是将转角传感器测得的信号输入到泊车控制器, 然后将利用接口程序产生的模拟转矩传感器的信号输入到EPS控制器当中, 这大大减少了硬件成本和开发成本。

泊车阶段, 转矩传感器测量会发生各种超调, 导致测量结果不准确, 所以在此阶段, 转矩传感器是处于被屏蔽状态。这就需要使用转角传感器测得转角, 再利用转角与转矩之间的关系模拟出转矩传感器的信号作为EPS的一个输入。转角与转矩之间的关系, 一般使用多次试验, 用系统辨识的方式给出。

4 某型轿车泊车过程分析

4.1 泊车路径分析

仿真分析以某型轿车为例, 该车车长为4.315 m; 宽为1.783 m; 轴距为2.630 m; 前悬为1.030 m; 后悬为0.685 m; $\begin{matrix} K \end{matrix}$ 值取1/15。扫描到的泊车位情况为: $\begin{matrix} W_{1} = 6.5; W_{2} = 5.5; H_{1} = 3.3; H_{2} = 1, \end{matrix}$ 得到可行的泊车路径组, 按照路径最短的原则最优化得到泊车路径时车速为2.6 m/s, 方向盘转速为32° /s; $\begin{matrix} m \end{matrix}$ 为38.5° , 最终路径如图5所示。

	Figure Option View Download New Window
	图5 最优泊车路径Fig.5 Optimal parking path

4.2 车速和方向盘转速控制

经过多次尝试得到该型号轿车低速行驶情况下, 控制量 $\begin{matrix} u \end{matrix}$ 的PID控制器取值分别为:0.46, -0.68, 0.76时速度跟踪效果最优, 实际车速与期望车速对比如图6所示。

	Figure Option View Download New Window
	图6 实际车速与预期车速对比Fig.6 Comparison of actual speed and expected speed

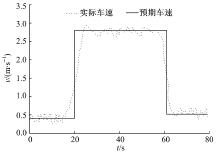
从图6可以看出, 车辆低速行驶时速度跟随效果良好, 基本可以满足泊车精度要求。

采用统计的方法来辨识转角与转矩之间的关系。这里采用的统计方法是在方向盘上加装电机, 利用转矩传感器测量转矩信息, 在不同的车速和方向盘转角、方向盘转速下得到转矩结果, 经过统计, 得到不同方向盘转角、方向盘转速和转矩的辨识结果如式(11)所示:

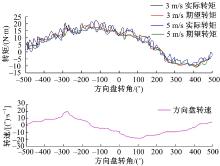
$\begin{matrix} \begin{matrix} G (s) = \\ \frac{5.986 s^{2} ω^{1.6} + 6.007 v^{2} s - 1.569 v^{3.5} ω}{s^{3} + 96.525 s^{2} v^{1.7} ω + 12.654 s + 1.258 ψwv} \end{matrix} \end{matrix}$ (11)

图7为在车速分别为3 m/s和5 m/s时的系统辨识的结果。其中实线是实际测得的力矩大小, 虚线是经过辨识后预期的力矩大小。计算得到, 车速为3 m/s时, 实际力矩与预期力矩的残差平方为0.132, 拟合度为0.965; 车速为5 m/s时, 实际力矩与预期力矩的残差平方为0.156, 拟合度为0.982。从图7也可以看出, 实际力矩对预期力矩的跟踪效果良好, 所得到的模型是非常切合实际的。

	Figure Option View Download New Window
	图7 力矩与转速关系的系统辨识图Fig.7 System identification for relationship between torque and rotational speed

对本文的五段式泊车与市场上比较成熟的两段式泊车的车速、方向盘转角、油门踏板的行程、刹车行程随时间的变化情况进行了对比, 结果如图8所示。

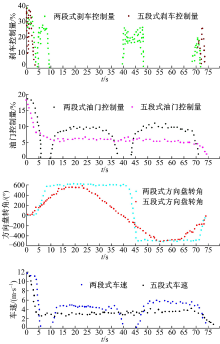	Figure Option View Download New Window
	图8 车速、方向盘转角、油门及刹车控制量随时间变化Fig.8 Change of vehicle speed, steering wheel angle, accelerator and brake with time

从图8中可以看出:使用五段式泊车, 车速、转角和油门的变化比较平缓, 刹车过程只发生在开始和结尾阶段, 说明整个泊车过程比较平缓且连贯性良好; 而使用两段式泊车时, 车速频繁变化, 需要频繁切换刹车和油门, 且方向盘转动比较急促, 乘坐舒适性较低。

5 结论

(1)研究了车辆低速行驶、方向盘匀速转动时, 车辆后轴中心点的轨迹, 得到了后轴中心点X坐标、Y坐标和切角的轨迹方程。

(2)基于方向盘匀速转动下车辆的轨迹方程设计了泊车轨迹, 泊车过程分为5个阶段, 并且基于车辆避撞要求提出了求解泊车轨迹中参数的方法。仿真结果验证了轨迹及求解参数方法的正确性。

(3)基于速度恒定设计基于PID反馈调节的车速恒定控制器, 试验证明速度跟踪效果良好。基于车辆方向盘转速恒定提出了基于负反馈的转速控制系统, 该系统充分利用了EPS原有的资源, 其中力矩与转速的关系也得到了试验验证。

(4)通过试验表明了整个泊车过程平稳、连贯性良好、乘员舒适性较好。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	魏振亚. 基于超声波车位探测系统的自动泊车方法研究[D]. 合肥: 合肥工业大学机械与车辆工程学院, 2013. Wei Zhen-ya. Research on automatic parking based on ultrasonic detecting system[D]. Hefei: School of Mechanical and Automotive Engineering, Hefei University of Technology, 2013. [本文引用:1]
[2]	王旭东. 基于环视的自动泊车方法研究与系统设计[D]. 上海: 上海交通大学机械与动力工程学院, 2013. Wang Xu-dong. Autonomous parking system research and design based on bird's eye view[D]. Shanghai: School of Mechanical Engineering, Shanghai Jiao Tong University, 2013. [本文引用:1]
[3]	Carlos M S, Matilde S P, Luis G S. A fuzzy decision system for an autonomous car parking[J]. Intelligent Systems Reference Library, 2012, 33(2): 237-258. [本文引用:1]
[4]	王芳成. 自动平行泊车系统的研究[D]. 合肥: 中国科学技术大学工程科学学院, 2010. Wang F C. Research of automatic parallel parking system[D]. Hefei: School of Engineering Science, University of Science and Technology of China, 2010. [本文引用:1]
[5]	姜辉, 郭孔辉, 张建伟. 基于路径规划的自动平行泊车转向控制器[J] . 吉林大学学报: 工学版, 2011, 41(2): 293-297. Jiang Hui, Guo Kong-hui, Zhang Jian-wei. Design of automatic parallel parking steering controller based on path-planning[J]. Journal of Jilin University (Engineering and Technology), 2011, 41(2): 293-297. [本文引用:1]
[6]	Maekawa T, Noda T, Tamura S, et al. Curvature continuous path generation for autonomous vehicle using β-spline curves[J]. Computer-Aided Design, 2010, 42(4): 350-359. [本文引用:1]
[7]	Zhang S W, Simkani M, Zadeh M H. Automatic vehicle parallel parking design using fifth degree polynomial path planning[C]//Vehicular Technology Conference, Budapest, 2011: 1-4. [本文引用:1]
[8]	Zhao L, Zheng G Q, Li J S. Automatic parking path optimization based on Bezier curve fitting[C]//Proc of IEEE International Conference on Automation and Logistics, Zhengzhou, China, 2012: 583-587. [本文引用:1]
[9]	张野, 陈慧, 程昆朋. 基于两步法的平行泊车分段路径规划算法[J]. 计算机仿真, 2013(6): 169-173. Zhang Ye, Chen Hui, Cheng Kun-peng. Path planning method for parallel parking assist system[J]. Computer Simulation, 2013(6): 169-173. [本文引用:1]
[10]	王道斌, 梁华为, 杨妮娜, 等. 两种自主泊车路径规划方法的对比研究[J]. 电子测量技术, 2011, 34(1): 27-38. Wang Dao-bin, Liang Hua-wei, Yang Ni-na, et al. On path planning of two self-parking methods[J]. Electronic Measurement Technology, 2011, 34(1): 27-38. [本文引用:1]
[11]	周培义. 单目视觉自动泊车控制系统研究[D]. 长沙: 湖南大学机械与运载工程学院, 2014. Zhou Pei-yi. Research on monocular vision automatic parking control system[D]. Changsha: College of Mechanical and Vehicle Engneering, School of Automotive Engineering, Hunan University, 2014. [本文引用:1]
[12]	姜辉. 自动平行泊车系统转向控制策略的研究[D]. 长春: 吉林大学汽车工程学院, 2010. Jiang H. Research on strategies of automatic parallel parking steering control[D]. Changchun: College of Automotive Engineering, Jilin University, 2010. [本文引用:1]
[13]	Li Y C, Song J F, Zeng J. A study on the calculation and verification methods of accident vehicle velocity based on the uncertainty theory[C]//8th Forum of Automotive Traffic Safety, Wuhu, China, 2010: 285-290. [本文引用:1]
[14]	Zhao J, El K A. Coordinated throttle and brake fuzzy controller design for vehicle following[C]//2010 13th International IEEE Conference on Intelligent Transportation Systems (ITSC), Funchal, 2010: 659-664. [本文引用:1]
[15]	姜永, 解晓琳. 汽车自动驾驶的方向与车速控制方法设计[J]. 科学技术与工程, 2013, 13(34): 10213-10220. Jiang Yong, Xie Xiao-lin. Design of steering and speed control algorithms for automatics driving of automobiles[J]. Science Technology and Engineering, 2013, 13(34): 10213-10220. [本文引用:1]
[16]	尚世亮. 自动平行泊车车位超声波探测与转向控制算法研究[D]. 长春: 吉林大学汽车工程学院, 2009. Shang S L. Research on ultrasonic detection of parking slot and steering control algorithm for automatic parallel parking[D]. Changchun: College of Automotive Engineering, Jilin University, 2009. [本文引用:1]

2013

0.0

... 目前,泊车外部环境建模技术已经比较成熟,主要是基于超声波雷达测距和双目成像原理建立泊车外部环境^[1,2] ...

2013

0.0

. 2013, :-

Autonomous parking system research and design based on bird's eye view

基于环视的自动泊车方法研究与系统设计[D]

Wang Xu-dong.

王旭东

... 目前,泊车外部环境建模技术已经比较成熟,主要是基于超声波雷达测距和双目成像原理建立泊车外部环境^[1,2] ...

2012

0.0

... 研究热点主要集中在泊车路径的规划,主要有3种路径规划方式:文献^[3,4,5]采用模糊控制的策略,提出了来回多段移动式的泊车路径规划方法 ...

2010

0.0

. 2010, :- DOI:doi:10.7666/d.y1705875

Research of automatic parallel parking system

自动平行泊车系统的研究[D]

Wang F C.

王芳成

随着汽车保有量的快速上升，在现代都市中“停车难”问题表现的越来越突出。将车辆停入一个窄小的停车位，对很多驾驶员来说不是件容易的事，尤其是一些初学者，由此引发的交通事故也逐年增加。一个有效的自动泊车系统，不仅能帮助驾驶者快速、安全的完成泊车操作，从而减轻驾驶员负担，减少交通事故，而且能够有效提高汽车的智能化程度，增加汽车的附加值，从而带来巨大的经济效益。　　本文设计了一种自动平行泊车系统。首先分析了车辆泊车时低速情况下，车辆运动学模型和车辆转弯半径与方向盘转角的关系。根据运动学模型和实际泊车过程，研究了平行泊车的几...

... 研究热点主要集中在泊车路径的规划,主要有3种路径规划方式:文献^[3,4,5]采用模糊控制的策略,提出了来回多段移动式的泊车路径规划方法 ...

2011

0.0

. 2011, 41(2):293-297

Design of automatic parallel parking steering controller based on path-planning

基于路径规划的自动平行泊车转向控制器

Jiang Hui , Guo Kong-hui , Zhang Jian-wei.

姜辉, 郭孔辉, 张建伟

摘　要：分析了汽车低速倒车过程中的运动学特性,以及汽车在倒车过程中车身与停车位以及障碍物之间可能发生的碰撞,同时根据汽车与车位之间的几何约束规划倒车路径,确定平行泊车的预备倒车区域,实现平行泊车的转向策略,以便追踪规划的路径,避免发生碰撞。在SIM-ULINK中搭建某轿车的运动学模型以及模拟平行泊车的倒车环境。将转向控制策略引入应用SIMULINK所建立的系统中仿真模拟该轿车的平行泊车过程。通过仿真验证了该策略实现平行泊车的可行性。

... 研究热点主要集中在泊车路径的规划,主要有3种路径规划方式:文献^[3,4,5]采用模糊控制的策略,提出了来回多段移动式的泊车路径规划方法 ...

2010

0.0

... 文献^[6,7,8]提出了基于B样条曲线、五次多项式曲线、贝塞尔曲线等曲率连续的泊车路径规划方法 ...

2011

0.0

... 文献^[6,7,8]提出了基于B样条曲线、五次多项式曲线、贝塞尔曲线等曲率连续的泊车路径规划方法 ...

2012

0.0

... 文献^[6,7,8]提出了基于B样条曲线、五次多项式曲线、贝塞尔曲线等曲率连续的泊车路径规划方法 ...

2013

0.0

... 文献^[9]提出了由圆弧和直线组成的曲率不连续的泊车路径规划方法 ...

2011

0.0

. 2011, 34(1):27-38 DOI:doi:10.3969/j.issn.1002-7300.2011.01.006

On path planning of two self-parking methods

两种自主泊车路径规划方法的对比研究

Wang Dao-bin , Liang Hua-wei , Yang Ni-na

王道斌, 梁华为, 杨妮娜

路径规划是智能车辆导航的基本环节之一.根据车辆的运动学模型和实际的泊车过程提出了改进的最小半径和不等半径两种几何路径规划方法.经计算机仿真表明两种路径规划方法的适用范围均明显扩大,同时提出的两种方法的结合应用还能从整体上优化泊车过程.所提的方法对自主泊车的路径规划研究具有一定的参考价值.

... 基于曲率不连续的路径规划,特别是两段式泊车路径规划方法计算量小,但是泊车连贯性低^[10] ...

2014

0.0

... 文献^[11]提出了采用缓和曲线线型进行路径规划,将泊车路径分为七段,但未做深入研究 ...

2010

0.0

. 2010, :-

Research on strategies of automatic parallel parking steering control

自动平行泊车系统转向控制策略的研究[D]

Jiang H.

姜辉

目前,人们生活水平的提高,使得汽车拥有量大幅增加,致使城市各处停车场所拥挤不堪,导致汽车的转动空间越来越小,倒车问题日益显著。为了解决这一难题,自动泊车系统成为目前汽车行业最为热门的研究课题之一。本文的主旨是在尽量小的停车空间内,找到比较好的泊车转向控制策略。首先采用多年来对倒车问题的解决已经相对成熟的模糊控制技术来解决平行泊车的控制问题,分析其不足,并采用两种方案来解决其不足之处。本文分析了汽车在低速倒车过程中的运动学特性以及汽车低速下的转向特性,以此为基础设计自动平行泊车的两圆弧相切的倒车轨迹;根据极限转弯特性估算目标车辆平行泊车停车空间范围;分析汽车在平行泊车过程中,汽车与停车位的可能性碰撞,确定停车位的大小,规划汽车可以成功泊车的所有的倒车轨迹,制定相应的平行泊车倒车控制策略;同时以倒车规范的许可范围内的不同速度倒车,根据车身顶点的碰撞修正最小停车空间;采用连续曲线逼近原两圆弧相切的轨迹,弥补转向盘转角突变的问题;为更好的分析汽车平行泊车时的倒车规律及其特点,做平行泊车实验,采集平行泊车数据,对其进行分析处理,减少运算量及出错率;最后基于自适应神经网络对实验数据推理分析提取平行泊车的模糊推理系统;针对两种控制策略,在MATLAB/simulink下建立的倒车环境中进行泊车仿真实验,比较两种控制策略的优缺点,证明了两种策略的泊车的可行性、合理性。

... 根据文献^[12],车辆在低速运动时,不计车轮的侧向滑动,车辆后轴中心点的瞬时半径R=lcot#cod#x003c8 ...

2010

0.0

... 车辆的加、减速操作对应的油门的开合和制动踏板的切换关系在文献^[13,14,15]中有具体阐述 ...

2010

0.0

... 车辆的加、减速操作对应的油门的开合和制动踏板的切换关系在文献^[13,14,15]中有具体阐述 ...

2013

0.0

. 2013, 13(34):10213-10220 DOI:doi:10.3969/j.issn.1671-1815.2013.34.021

Design of steering and speed control algorithms for automatics driving of automobiles

汽车自动驾驶的方向与车速控制方法设计

Jiang Yong , Xie Xiao-lin.

姜永, 解晓琳

用于港口集装箱转运和路面疲劳试验加载等场合的半挂汽车列车运输具有线路固定和场地封闭等特点,采用自动驾驶将提高行车安全、减少人力成本。以半挂汽车列车为控制对象,设计了汽车自动驾驶的方向和车速控制算法。采用基于侧向位置偏差和航向偏差联合控制参数的方向控制策略。为增强方向控制算法对不同车速的适应性,引入基于稳态转向增益的方向控制增益调度。车速控制采用预瞄位置期望车速与当前实际车速的偏差反馈PID控制。以油门开度与制动踏板行程为非相容组合控制输入,依据期望纵向加速度确定不同控制输入方式的切换及控制输入大小。采用Matlab/Simulink和TruckSim协同仿真手段评价自动驾驶控制效果。仿真结果表明在设定不同路径和目标车速下,提出的算法均能以较小侧向位置偏差、航向偏差和车速误差实现路径和车速跟踪。

... 车辆的加、减速操作对应的油门的开合和制动踏板的切换关系在文献^[13,14,15]中有具体阐述 ...

2009

0.0

. 2009, :-

Research on ultrasonic detection of parking slot and steering control algorithm for automatic parallel parking

自动平行泊车车位超声波探测与转向控制算法研究[D]

Shang S L.

尚世亮

自动泊车是车辆自动的从行驶车道运动到停车位的机动行为,包括自动平行泊车、倒库及成一定角度泊车。开发自动泊车系统的目的在于,将驾驶员从复杂的泊车操作中解脱出来,提高驾驶的舒适性。实现自动泊车的关键是对车位的有效探测和泊车时的转向控制。本文主要针对平行泊车工况,首先对自动泊车车位超声探测方法展开研究,包括超声探测系统的硬件及软件开发,并在此基础上完成车位探测试验,提出自动泊车车位超声探测修正方法。其次提出基于四个时间变量的平行泊车转向控制规律,并在veDYNA车辆动力学模型上实现平行泊车的仿真,以此为基础,得到经过遗传算法优化的平行泊车转向控制策略。最后对泊车转向的电机控制展开讨论,根据优化得到的转向控制策略控制电机运行,并进行自动平行泊车转向控制实车试验,验证转向控制策略的有效性。本文提出了自动平行泊车车位超声探测修正方法和泊车转向控制算法,并通过试验验证了其有效性。

... 文献^[16]中,方向盘转速的控制是通过在方向盘上安装转向电机实现,或者在EPS系统中加装方向盘转角传感器通过闭环调节来达到预期的转速,这些方法在试验中可行,大规模的生产中受到安装和成本的制约 ...