崎岖地形环境下四足机器人的静步态规划方法

引用本文

张帅帅, 荣学文, 李贻斌, 李彬. 崎岖地形环境下四足机器人的静步态规划方法.吉林大学学报:工学版, 2016, 46(4): 1287-1296
ZHANG Shuai-shuai, RONG Xue-wen, LI Yi-bin, LI Bin. Static gait planning method for quadruped robots on rough terrains. Journal of Jilin University Engineering and Technology Edition, 2016, 46(4): 1287-1296 复制到剪切板

Permissions

崎岖地形环境下四足机器人的静步态规划方法

张帅帅¹, 荣学文¹, 李贻斌¹, 李彬²

1.山东大学控制科学与工程学院, 济南 250061

2.齐鲁工业大学理学院, 济南 250353

通讯作者：荣学文(1973),男,高级工程师.研究方向:机器人技术,智能控制理论.E-mail:rongxw@sdu.edu.cn

作者简介:张帅帅(1986-),男,博士研究生.研究方向:四足机器人,智能控制系统.E-mail:zhangshuaisdu@163.com

基金:国家自然科学基金重点项目(61233014); “863”国家高技术研究发展计划项目(2015AA042201); 国家自然科学基金项目(61305130); 中国博士后科学基金项目(2013M541912)

摘要

为了使四足机器人能够通过姿态调整提高其自身的地形适应性,给出了机器人姿态调整角的计算方法。四足机器人在行走过程中通过躯干的摆动增加稳定裕度,并使用五次曲线对躯干运动轨迹进行规划,保证了整个运动过程的连续性。另外,为克服机器人无法获取地形信息的不足,规划了一种矩形摆动足足底轨迹。仿真实验结果表明:使用提出的静步态规划方法,四足机器人可以在未知地形信息的情况下,实时、自主、稳定地通过复杂度较高的崎岖地形。

关键词: 自动控制技术; 四足机器人; 静步态规划; 躯干运动曲线; 足底轨迹

中图分类号:TP242.6 文献标志码:A 文章编号:1671-5497(2016)04-1287-10

Static gait planning method for quadruped robots on rough terrains

ZHANG Shuai-shuai¹, RONG Xue-wen¹, LI Yi-bin¹, LI Bin²

1.School of Control Science and Engineering, Shandong University, Ji'nan 250061, China

2.School of Science, Qilu University of Technology, Ji'nan 250353, China

Abstract

In order to improve the ability of quadruped robots to cross rough terrains, a static gait planning method is proposed. This method consists of three parts: the posture adjustment planning, the body trajectory planning and the foot trajectory planning. To improve the adaptability of the quadruped robot to the terrain through the posture adjustment, a method to calculate the pitching angle is proposed. The robot can obtain enough stability margin through a body sway motion, and the continuity of movement during the whole walking process can be guaranteed by using a quintic body trajectory. In addition, a box shape foot trajectory planning method is given to overcome the situation that the robot can not obtain the information of the terrain. Using the proposed static gait planning method, the robot can autonomously navigate through unknown irregular terrains with sufficient stability margin in real time.

Keyword: automatic control technology; quadruped robot; static gait planning; body moving trajectory; foot trajectory

Show Figures

0 引言

四足机器人能够在崎岖度较高, 甚至是一些对于轮式和履带式机器人无法跨越的复杂地形上行走^[1]。在四足机器人的诸多研究领域中, 机器人的步态规划是最基本、最重要的方面之一。一个鲁棒性强的步态能够帮助机器人顺利地通过多种类型的崎岖地形, 尤其是那些非结构化的复杂地形。

为顺利通过崎岖度较高的地形, 四足机器人一般选用静步态来增大自身的稳定性。在静步态研究方面, McGhee等^[2]首先给出了四足机器人静步态的数学描述。之后, 国内外许多学者提出了四足机器人静步态规划的方法。其中, 比较典型的有:Lee等^[3]提出的静步态规划方法, 并详细分析了机器人使用静步态行走时的稳定性; 针对“ Little Dog” 机器人进行的相关静步态规划^{[4, 5, 6, 7]}; 黄博等^[8]对机器人爬越楼梯时的静步态进行了规划; 王鹏飞^[9]根据机器人在迈步阶段躯干是否移动, 将四足机器人的静步态分为间歇爬行步态和连续爬行步态, 并对这两种步态的稳定性等方面进行了规划和分析; 冯华山等^[10]对四足机器人在坡面静步态平衡方法进行了相关的研究, 着重分析了四足机器人在坡面行走的过渡状态下姿态的变化情况以及稳定行走的方法; 高彬^[11]对四足机器人使用静步态进行全方位转向做了相关研究。

现有的四足机器人静步态规划中, 有的只规划了机器人躯干在前进方向上的运动^{[3, 8, 9, 10, 11]}, 这种情况下, 机器人在行走过程中稳定裕度相对较小; 有的虽然增加了侧向移动但是不能保证机器人的重心一直向前运动^[4], 降低了机器人的平均运动速度和能量利用效率; 有的没有结合姿态调整和足底轨迹规划以提高机器人跨越复杂地形的能力^{[3, 5, 9]}。

针对以上不足, 本文给出了一种四足机器人静步态生成方法, 提出了具有较好地形适应性和鲁棒性的躯干运动轨迹规划方法、足底轨迹规划方法以及姿态调整方法。根据四只支撑足的位置以及躯干的姿态信息, 给出了机器人躯干运动轨迹的规划方法, 本文方法既能有效增大机器人的稳定裕度, 又能保证机器人在运动过程中躯干一直向前运动且运动速度和加速度连续, 从而在保证机器人静态稳定性的前提下, 提高机器人的平均运动速度及能量利用率。为保证四足机器人的摆动足具有足够的有效工作空间, 以使机器人能够跨越更高的障碍物, 本文提出了一种姿态调整方法, 提高了四足机器人的地形适应性; 另外, 本文给出的摆动足足底轨迹规划方法, 使机器人在不能获知地形信息的情况下, 依然能够保证摆动足顺利摆动至目标落足点。仿真实验验证了本文方法的正确性和有效性。

1 四足机器人静态稳定性及其迈步顺序

1.1 四足机器人的静态稳定性

具有一定的静态稳定裕度是四足机器人在使用静步态行走时的基本要求, 尤其是当四足机器人行走在崎岖度较高的地形上时。

为了准确而有效地衡量机器人的静态稳定性, 目前存在多种稳定裕度的计算方法, 例如纵向稳定裕度(Longitudinal stability margin)^[13]、绝对稳定裕度(Absolute stability margin)^[14]、能量稳定裕度(Energy stability margin)^[15]等。在这些稳定裕度计算方法中, 绝对稳定裕度的计算方法相对简单, 且能准确地衡量机器人的静态稳定裕度, 因而在本文方法中选用绝对稳定裕度来衡量机器人的稳定性。

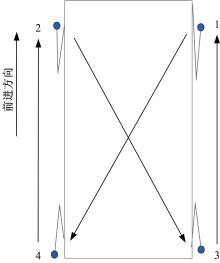
四足机器人重心在水平面上的投影到支撑多边形各边距离的最小值为机器人的绝对稳定裕度。图1为四足机器人支撑三角形内稳定裕度的分布。此时, 4号足处于摆动相, 其余三只足处于支撑相。当机器人重心的投影位于支撑三角形的内心时, 其到支撑三角形三边的距离相等, 此时, 机器人的稳定裕度最大。

	Figure Option View Download New Window
	图1 支撑三角形内稳定裕度的分布Fig.1 Distribution of stability margin within support triangle

1.2 机器人的静步态迈步顺序

对于四足机器人而言, 共有6种非奇异的静步态迈步顺序^[2], 在这6种迈步顺序中, 4-2-3-1为稳定裕度最优的迈步顺序^[12], 其中, 机器人足的编号如图2所示。因而, 在本文中的静步态规划中, 采用4-2-3-1的迈步顺序。

	Figure Option View Download New Window
	图2 四足机器人足的编号及迈步顺序Fig.2 Serial numbers of feet and step sequence of quadruped robot

四足机器人在摆动不同的足时所对应的支撑三角形是不同的, 但是位于身体同侧的足所对应的支撑三角形存在重合的区域, 这个重合区域被称为双支撑三角形(Double support triangle)^[7]。当机器人重心的投影位于这个区域时, 机器人就能够连续地按照迈步顺序依次摆动位于躯干同侧的足。

为提高机器人在使用静步态行走时的鲁棒性, 一般会设定一个最小稳定裕度S_min, 只有当机器人的稳定裕度不小于S_min时, 机器人才被认为是稳定的。但是, 由于S_min的存在, 使得位于躯干左右两侧足所对应的稳定区域是不连续的^[5]。因此, 为保证机器人连续、稳定地按照迈步顺序向前行走, 本文规划的静步态中增加了四足支撑阶段。在四足支撑阶段中, 机器人通过四只足的支撑运动将其重心调整到对应的稳定区域。结合迈步顺序, 可以得到机器人使用静步态行走时的步态图, 如图3所示, 由图3可以看出在每只后足(3号足或4号足)摆动之前都有一个四足支撑阶段, 以保证机器人在迈步阶段的稳定性。

	Figure Option View Download New Window
	图3 四足机器人静步态行走的步态图Fig.3 Gait diagram of quadruped robot walking with static gait

2 四足机器人的静步态规划

2.1 姿态调整规划

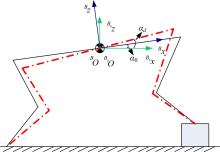
四足机器人在行走过程中, 由于地形的起伏而使四只足的落足位置高低不一, 依据前、后足落足点之间的高度差异主动地调整躯干的俯仰角(Pitching angle), 可以增大各足的有效工作空间, 进而可使机器人能够跨越更高的障碍物。姿态调整规划中最重要的是求得期望的俯仰角调整角度, 下面将详细描述这个角度的求解过程。

假设在四足支撑阶段, 机器人第 i只足在坐标系{B}中的坐标为^BP_i (^Bx_i , ^By_i , ^Bz_i),i∈(1,2,3,4)。设定一个初始坐标系{B₀},,如图4所示, 其原点与机体坐标系原点重合, $\begin{matrix} _{}^{B_{0}} x \end{matrix}$ 轴与水平地面平行并指向前进方向; $\begin{matrix} _{}^{B_{0}} z \end{matrix}$ 轴指向重力的反方向;^B0 y轴与机体坐标系{B}的^By轴重合。

	Figure Option View Download New Window
	图4 机器人俯仰角的计算Fig.4 Calculation of pitching angle of robot

假设机器人在姿态调整之前的初始俯仰角为α₀,即^B0 x与^B x的夹角为α₀,如图4所示。由此可得坐标系{B₀}与坐标系{B}之间的转换矩阵, 如式(1)所示:

$\begin{matrix} _{B}^{B_{0}} T = Rot (_{}^{B} y, - α_{0}) = [\begin{matrix} \cos α_{0} & 0 & - \sin α_{0} \\ 0 & 1 & 0 \\ \sin α_{0} & 0 & \cos α_{0} \end{matrix}] (1) \end{matrix}$

进而, 可得机器人四只足在 $\begin{matrix} {B_{0}} \end{matrix}$ 中的坐标值:

$\begin{matrix} \begin{matrix} ^{B_{0}} P_{i} = [\begin{matrix} _{}^{B_{0}} x_{i} \\ _{}^{B_{0}} y_{i} \\ _{}^{B_{0}} z_{i} \\ 1 \end{matrix}] =_{B}^{B_{0}} T \cdot_{}^{B} P_{i} = \\ [\begin{matrix} \cos α_{0} & 0 & - \sin α_{0} & 0 \\ 0 & 1 & 0 & 0 \\ \sin α_{0} & 0 & \cos α_{0} & 0 \\ 0 & 0 & 0 & 1 \end{matrix}] \cdot [\begin{matrix} _{}^{B} x_{i} \\ _{}^{B} y_{i} \\ _{}^{B} x_{i} \\ 1 \end{matrix}] = \\ [\begin{matrix} x_{i} \cdot cosα + z_{i} \cdot sinα \\ _{}^{B} y_{i} \\ z_{i} \cdot cosα - x_{i} \cdot sinα \\ 1 \end{matrix}] (2) \end{matrix} \end{matrix}$

式中:^B0P_i (^B0x_i , ^B0y_i , ^B0z_i),i∈(1,2,3,4)表示i号足在{B₀}中的坐标值。

然后, 分别计算前两只足(1号足和2号足)在^B0x轴上坐标值的平均值^x m_f和在 $\begin{matrix} _{}^{B_{0}} z \end{matrix}$ 轴上坐标值的平均值 $\begin{matrix} ^{z} m_{f}, \end{matrix}$ 如式(3)所示:

$\begin{matrix} \{\begin{matrix} ^{x} m_{f} = (_{}^{B_{0}} x_{1} +_{}^{B_{0}} x_{2} \frac{)}{2} \\ ^{z} m_{f} = (_{}^{B_{0}} z_{1} +_{}^{B_{0}} z_{2} \frac{)}{2} \end{matrix} (3) \end{matrix}$

计算后两只足(3号足和4号足)在^B0x轴上坐标值的平均值^xm_r 和在^B0z轴上坐标值的平均值^zm_r如式(4)所示:

$\begin{matrix} \{\begin{matrix} ^{x} m_{r} = (_{}^{B_{0}} x_{3} +_{}^{B_{0}} x_{4} \frac{)}{2} \\ ^{z} m_{r} = (_{}^{B_{0}} z_{3} +_{}^{B_{0}} z_{4} \frac{)}{2} \end{matrix} (4) \end{matrix}$

最后, 得到期望的俯仰角调整角度为:

$\begin{matrix} α_{d} = \arctan \frac{^{z} m_{r} -^{z} m_{f}}{^{x} m_{r} -^{x} m_{f}} (5) \end{matrix}$

2.2 躯干运动轨迹规划

本文是以非连续静步态为基础进行规划的, 当机器人在足的摆动阶段, 其躯干静止不动, 这样能够避免出现机器人在迈步阶段因足底滑动而失去稳定性的情况^[16]。机器人在四足支撑阶段完成重心的调整, 因而, 只需要对四足支撑阶段中的躯干运动轨迹进行规划。

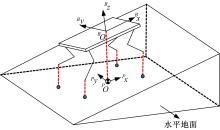
假设机器人躯干的质量均匀分布, 则机器人躯干的重心与躯干的几何中心重合, 躯干的摆动曲线即为躯干重心的摆动轨迹。在规划躯干调整轨迹时, 首先将机器的四只支撑足以及躯干的重心投影到水平地面上, 并设定一个平面坐标系 {P},如图5所示,然后通过四只支撑足投影在坐标系{P}中的坐标计算重心调整的目标位置并规划躯干运动轨迹。

	Figure Option View Download New Window
	图5 机器人支撑足在水平地面上的投影Fig.5 Ground projection of support feet of robot

为了保证机器人在足摆动过程中拥有较大的稳定裕度, 在四足支撑阶段将躯干重心在水平面上的投影调整至对应的双支撑三角形中稳定裕度最大的位置, 即以对应的双支撑三角形的内心为重心调整的目标位置。

	Figure Option View Download New Window
	图6 重心调整目标的位置计算Fig.6 Calculation of target position of adjustment

为了方便描述重心轨迹的规划过程, 将机器人在四足支撑阶段的足重新命名。如图6所示, 将按迈步顺序接下来要摆动的后足记为NSF(Next swing foot), 记此足的期望落足点为DF(Desired foothold), 与NSF位于躯干同侧的前足记为IFF(Ipsilateral front foot), 记与NSF位于躯干不同侧的两只足中的前足和后足分别为CFF(Contralateral front foot)和CHF(Contralateral hind foot)。假设这四只足的投影在 $\begin{matrix} {P} \end{matrix}$ 中的坐标分别为P_NSF(x_NSF, y_NSF), P_IFF(x_IFF, y_IFF), P_CFF(x_CFF, y_CFF), P_CHF(x_CHF, y_CHF), NSF期望落足点DF投影在坐标系 $\begin{matrix} {P} \end{matrix}$ 中的坐标为P_DF(x_DF, y_DF)。

根据点P_DF与点P_CFF的坐标, 可得直线L_DF-CFF的直线方程, 如式(6)所示:

$\begin{matrix} \begin{matrix} f_{DF - CFF} (x) = k_{DF - CFF} \cdot x + b_{DF - CFF} = \\ \frac{y_{DF} - y_{CFF}}{x_{DF} - x_{CFF}} \cdot x + y_{DF} - \frac{y_{DF} - y_{CFF}}{x_{DF} - x_{CFF}} \cdot x_{DF} (6) \end{matrix} \end{matrix}$

根据点P_IFF和点P_CHF的坐标, 可得直线L_IFF-CHF的直线方程, 如式(7)所示:

$\begin{matrix} \begin{matrix} f_{IFF - CHF} (x) = k_{IFF - CHF} \cdot x + b_{IFF - CHF} = \\ \frac{y_{IFF} - y_{CHF}}{x_{IFF} - x_{CHF}} \cdot x + y_{IFF} - \\ \frac{y_{IFF} - y_{CHF}}{x_{IFF} - x_{CHF}} \cdot x_{IFF} (7) \end{matrix} \end{matrix}$

设直线L_DF-CFF与直线L_IFF-CHF的交点为 P_I (x_I,y_I),则可得P_I的坐标值为:

$\begin{matrix} \{\begin{matrix} x_{I} = \frac{b_{IFF - CHF} - b_{DF - CFF}}{k_{DF - CFF} - k_{IFF - CHF}} \\ y_{I} = k_{DF - CFF} \cdot x_{I} + b_{DF - CFF} \end{matrix} (8) \end{matrix}$

三角形 $\begin{matrix} △ P_{I} P_{CHF} P_{CFF} \end{matrix}$ 为NSF与IFF相对应的双支撑三角形。

由相关点的坐标, 可得线段L_I_-CHF、线段L_I_-CFF、线段L_CFF-CHF的长度分别为:

$\begin{matrix} \{\begin{matrix} |L_{I - CHF}| = \sqrt[]{(x_{I} - x_{CHF})^{2} + (y_{I} - y_{CHF})^{2}} \\ |L_{I - CFF}| = \sqrt[]{(x_{I} - x_{CFF})^{2} + (y_{I} - y_{CFF})^{2}} \\ |L_{CFF - CHF}| = \sqrt[]{(x_{CFF} - x_{CHF})^{2} + (y_{CFF} - y_{CHF})^{2}} \end{matrix} (9) \end{matrix}$

进而, 可得支撑三角形 $\begin{matrix} △ P_{I} P_{CHF} P_{CFF} \end{matrix}$ 的内心坐标, 也就是重心调整的目标位置为:

$\begin{matrix} \{\begin{matrix} x_{D} = \\ \frac{|L_{I - CHF}| \cdot x_{CFF} + |L_{I - CFF}| \cdot x_{CHF} + |L_{CFF - CHF}| \cdot x_{I}}{|L_{I - CHF}| + |L_{I - CFF}| + |L_{CFF - CHF}|} \\ y_{D} = \\ \frac{|L_{I - CHF}| \cdot y_{CFF} + |L_{I - CFF}| \cdot y_{CHF} + |L_{CFF - CHF}| \cdot y_{I}}{|L_{I - CHF}| + |L_{I - CFF}| + |L_{CFF - CHF}|} \end{matrix} (10) \end{matrix}$

坐标系 $\begin{matrix} {P} \end{matrix}$ 的原点与四足支撑阶段开始时重心的投影点重合, 该点为重心调整的初始位置。由图3可知, 在四足支撑阶段之前和之后都是足的摆动阶段。对于非连续静步态, 在足的摆动阶段, 机器人的躯干静止, 其速度和加速度均为零。因而, 为保证机器人在整个运动过程中的连续性, 在躯干摆动的起始和终止点时, 机器人躯干运动轨迹的速度和加速度应均为零。本文中使用五次曲线规划重心的移动轨迹, 使机器人的重心在运动到目标位置的同时, 保证躯干运动速度和加速度的连续性。由此可得机器人在四足支撑阶段躯干运动轨迹的方程为:

$\begin{matrix} \{\begin{matrix} x (t) = \frac{6 \cdot x_{D}}{T_{adj}^{5}} \cdot t^{5} + \frac{- 15 \cdot x_{D}}{T_{adj}^{4}} \cdot t^{4} + \frac{10 \cdot x_{D}}{T_{a dj}^{3}} \cdot t^{3} \\ y (t) = \frac{6 \cdot y_{D}}{T_{adj}^{5}} \cdot t^{5} + \frac{- 15 \cdot y_{D}}{T_{adj}^{4}} \cdot t^{4} + \frac{10 \cdot y_{D}}{T_{adj}^{3}} \cdot t^{3} \end{matrix} (11) \end{matrix}$

式中:T_adj为机器人完成重心调整所需要的时间; $\begin{matrix} x_{D} 和 y_{D} \end{matrix}$ 由式(10)求得。

通过在四足支撑阶段的重心调整, 四足机器人能够有效地增大其在运动过程中的静态稳定裕度。这样, 四足机器人就能够有效地避免因受到来自地形环境或自身意外扰动而使其处于失去稳定性的异常状态。同时, 也增强了四足机器人静步态规划算法的鲁棒性。

2.3 摆动足足底轨迹规划

四足机器人摆动足的运动轨迹规划是机器人步态规划的基本组成部分。四足机器人的摆动足应该准确地摆动至期望的落足点, 并且在运动的过程中不与地形中的障碍物发生碰撞。

如果可以获取地形信息, 机器人能够根据对地形特征规划最优的摆动足摆动轨迹, 但是在本文中的四足机器人上没有任何机载的地形感知设备, 机器人无法获得所行走地形的地形信息。为此, 本文中规划了一种矩形摆动曲线, 能够保证机器人在无法获得地形信息的情况下顺利完成摆动足的摆动。当四足机器人的摆动足沿本文中提出的摆动足足底轨迹向前迈步时, 能够保证摆动足在向前运动的过程中始终与地面保持一定的距离。这样, 就能够避免出现因机器人的摆动足在运动的过程中与地形中的障碍物发生碰撞而导致机器人迈步失败甚至失去稳定性的异常状态。

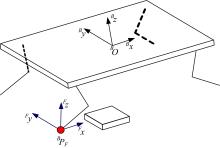
	Figure Option View Download New Window
	图7 足底坐标系{F}Fig.7 Foot coordinate frame {F}

设定一个足底坐标系 $\begin{matrix} {F}, 其原点为摆动足在抬离地面之前与地面的接触点^{B} P_{F}, 如图 7 所示。下面将首先规划摆动足相对于坐标系 {F} 的摆动轨迹, 然后通过坐标系 {F} 与坐标系 {B} 之间的关系, 求得摆动足相对于坐标系 {B} \end{matrix}$ 的摆动轨迹。

2.3.1 摆动足相对于坐标系 $\begin{matrix} {F} \end{matrix}$ 的摆动轨迹

如图8所示, 本文中提出的足底摆动轨迹分为三个阶段:垂直抬起阶段、前向摆动阶段和垂直下落阶段。假设机器人摆动足完成摆动的规划运动时间为T_sw。为避免因摆动足在垂直下落阶段运动速度过快造成落地时产生较大的接触力而影响机器人的稳定性, 机器人在前两个阶段(垂直抬起阶段和前向摆动阶段)用时为整个摆动足规划运动时间的一半, 即T_sw/2。剩余的T_sw/2的时间用以完成第三个阶段(垂直下落阶段), 这样可以有效地降低摆动足的下落速度, 进而减小摆动足接触地面时产生的冲击力, 消除影响机器人稳定的不利因素。

	Figure Option View Download New Window
	图8 期望落足点低于起始点时的足底摆动轨迹Fig.8 Foot trajectory when target foothold of swing foot below start point of swing foot

下面分别给出足底摆动轨迹三部分的方程:

(1)垂直抬起阶段

在垂直抬起阶段, 四足机器人的摆动足沿^F z方向匀速上升一定的距离H,使摆动足在向前迈进的过程中与地面保持一定的距离,以保证摆动足在向前迈进的时不与地形中凸起的障碍物发生碰撞。在这一阶段中,机器人的足只沿^F z 以保证摆动足在向前迈进的时候不与地形中凸起的障碍物发生碰撞。在这一阶段中, 机器人的足只沿Fz方向运动, 则可得到足底轨迹在第一部分的方程为:

$\begin{matrix} \{\begin{matrix} _{}^{F} x_{1} (t) = 0 \\ _{}^{F} y_{1} (t) = 0 \\ _{}^{F} z_{1} (t) = \frac{4 \cdot H}{T_{sw}} \cdot t \end{matrix} (12) \end{matrix}$

式中: $\begin{matrix} t \in [0, \frac{T_{sw}}{4}] 。 \end{matrix}$

(2)前向摆动阶段

假设机器人摆动足的期望落足点与点^F P沿^F x和^F y方向上的距离分别为L_x 和L_y。在前向摆动阶段中摆动足向前摆动至目标落足点沿^Fz 方向的正上方, 由此可得到足底轨迹在这个阶段的方程为:

$\begin{matrix} \{\begin{matrix} _{}^{F} x_{2} (t) = \frac{4 \cdot L_{x}}{T_{sw}} \cdot (t - \frac{T_{sw}}{4}), \\ _{}^{F} y_{2} (t) = \frac{4 \cdot L_{y}}{T_{sw}} \cdot (t - \frac{t_{sw}}{4}) \\ _{}^{F} z_{2} (t) = 0 \end{matrix} (13) \end{matrix}$

式中: $\begin{matrix} t \in [\frac{T_{sw}}{4}, \frac{T_{sw}}{2}] 。 \end{matrix}$

(3)垂直下落阶段

在垂直下落阶段, 机器人的摆动足只沿 $\begin{matrix} ^{F} z \end{matrix}$ 方向匀速向下运动。为保证当机器人摆动足的期望落足点高度在 $\begin{matrix} ^{F} z \end{matrix}$ 方向上比起始落足点低时(如图8所示, 其中虚线一端正方形代表的位置为摆动足的起始点, 虚线另一端三角形代表的位置为摆动足的期望落足点), 摆动足能够一直下落, 直到触地传感器检测到摆动足触碰到地面, 以一个系数 $\begin{matrix} k \end{matrix}$ 乘以摆动足的垂直下落速度, 则足底轨迹在第三部分的方程为:

$\begin{matrix} \{\begin{matrix} _{}^{F} x_{3} (t) = L_{x} \\ _{}^{F} y_{3} (t) = L_{y} \\ _{}^{F} z_{3} (t) = k \cdot \frac{2 \cdot H}{T_{sw}} \cdot (t - \frac{T_{sw}}{2}) \end{matrix} (14) \end{matrix}$

式中: $\begin{matrix} t \in [\frac{T_{sw}}{2}, T_{sw}] 。 \end{matrix}$

由式(12)~式(14)可得机器人的摆动足曲线在坐标系 $\begin{matrix} {F} \end{matrix}$ 中的方程为:

$\begin{matrix} \begin{matrix} _{}^{F} x (t) = \{\begin{matrix} _{}^{F} x_{1},, t \in [0, \frac{T_{sw}}{4}] \\ _{}^{F} x_{2}, t \in [\frac{T_{sw}}{4}, \frac{T_{sw}}{2}] \\ _{}^{F} x_{3}, t \in [\frac{T_{sw}}{2}, T_{sw}] \end{matrix} (15) \\ _{}^{F} y (t) = \{\begin{matrix} _{}^{F} y_{1}, t \in [0, \frac{T_{sw}}{4}] \\ _{}^{F} y_{2}, t \in [\frac{T_{sw}}{4}, \frac{T_{sw}}{2}] \\ _{}^{F} y_{3}, t \in [\frac{T_{sw}}{2}, T_{sw}] \end{matrix} (16) \\ _{}^{F} z (t) = \{\begin{matrix} _{}^{F} z_{1}, t \in [0, \frac{T_{sw}}{4}] \\ _{}^{F} z_{2}, t \in [\frac{T_{sw}}{4}, \frac{T_{sw}}{2}] \\ _{}^{F} z_{3}, t \in [\frac{T_{sw}}{2}, T_{sw}] \end{matrix} (17) \end{matrix} \end{matrix}$

2.3.2 摆动足相对于坐标系 $\begin{matrix} {B} \end{matrix}$ 的摆动轨迹

为了最终能够通过运动学的逆解得到机器人各关节的运动角度, 则需要求出足底运动轨迹在机体坐标系 $\begin{matrix} {B} \end{matrix}$ 中的表达式。

假设机器人在摆动足向前摆动时的俯仰角为α,点^BP_F在机体坐标系中的坐标为((^Bx_F ,^By_F ,^BZ_F),由此可得坐标系{F}与坐标系{B}之间的变换矩阵为：

$\begin{matrix} \begin{matrix} _{F}^{B} T = Trans (_{}^{B} x_{F},_{}^{B} y_{F},_{}^{B} z_{F}) \cdot Rot (_{}^{B} y, α) = \\ [\begin{matrix} cosα & 0 & sinα & _{}^{B} x_{F} \\ 0 & 1 & 0 & _{}^{B} y_{F} \\ - sinα & 0 & cosα & _{}^{B} z_{F} \\ 0 & 0 & 0 & 1 \end{matrix}] (18) \end{matrix} \end{matrix}$

根据 $\begin{matrix} _{F}^{B} T {, \end{matrix}$ 以及足底轨迹在坐标系{F}中的方程,可以得到机器人足底轨迹在机体坐标系{B} 中方程, 如式(19)所示:

$\begin{matrix} \begin{matrix} ^{B} P (t) = [\begin{matrix} _{}^{B} x (t) \\ _{}^{B} y (t) \\ _{}^{B} z (t) \\ 1 \end{matrix}] =_{F}^{B} T \cdot_{}^{F} P = \\ [\begin{matrix} cosα & 0 & sinα & _{}^{B} x_{F} \\ 0 & 1 & 0 & _{}^{B} y_{F} \\ - sinα & 0 & cosα & _{}^{B} z_{F} \\ 0 & 0 & 0 & 1 \end{matrix}] \cdot [\begin{matrix} _{}^{F} x (t) \\ _{}^{F} y (t) \\ _{}^{F} z (t) \\ 1 \end{matrix}] = \\ [\begin{matrix} _{}^{F} x (t) \cdot cosα +_{}^{F} z (t) \cdot sinα +_{}^{B} x_{F} \\ _{}^{F} y (t) +_{}^{B} y_{F} \\ -_{}^{F} x (t) \cdot sinα +_{}^{F} z (t) \cdot cosα +_{}^{B} z_{F} \\ 1 \end{matrix}] (19) \end{matrix} \end{matrix}$

3 仿真实验及结果分析

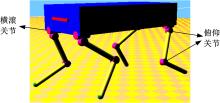
图9为机器人的仿真模型, 机器人每条腿具有三个自由度, 两个俯仰关节和一个横滚关节。

机器人躯干的长度为0.7 m, 宽为0.35 m, 自然站立时高度为0.55 m, 总质量为130 kg, 其中单腿质量为10 kg(躯干质量的11.1%)。在每只足的足底都安装有压力传感器, 用以感知机器人的触底信息; 在机器的躯干上安装有惯性测量单元用以检测机器人的姿态以及躯干的速度和加速度信息。

	Figure Option View Download New Window
	图9 四足机器人仿真模型Fig.9 Simulation model of quadruped robot

图10为在仿真环境中构建的崎岖地形, 地形包括三个部分:第一部分为大小不同、高度不一、随机散放的障碍物, 其中, 最高的障碍物高度为10 cm(机器人自然站立高度的18.2%), 最低高度为2 cm; 第二部分为斜度为17.2° 的斜坡; 第三部分为平坦的水平平台。

对四足机器人而言, 图10所示的复杂地形为未知、不确定的地形环境。机器人在行走的过程中根据本文方法实时规划相关运动, 以稳定、自主地通过该复杂地形。

	Figure Option View Download New Window
	图10 通过仿真软件构建的崎岖地形Fig.10 Rough terrain constructed by simulation software

图11为仿真实验截图。机器人能够自主、稳定地通过这个复杂地形。

	Figure Option View Download New Window
	图11 机器人通过复杂地形仿真实验截图Fig.11 Sequence of snapshots of robot while traversing rough terrain

	Figure Option View Download New Window
	图12 机器人躯干在前进方向上的运动轨迹Fig.12 Position variation curve of robot's body in moving direction

图12为四足机器人躯干的重心在前进方向上的移动轨迹, 由此看出, 机器人的移动轨迹连续且重心一直向前运动。在保证机器人稳定性的前提下, 消除了机器人躯干的后向运动, 能够有效地提高四足机器人在崎岖地形上行走过程中的平均运动速度和能量使用效率。

图13为四足机器人躯干的重心在侧方向上的移动轨迹。机器人能够在行走过程中根据本文算法自动计算重心调整量, 并根据自动规划的躯干摆动轨迹完成调整, 通过躯干在侧方向上的摆动, 增加机器人的稳定裕度。

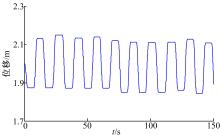	Figure Option View Download New Window
	图13 机器人躯干在侧方向上的运动轨迹Fig.13 Position variation curve of robot’ s body in side direction with respect to moving direction

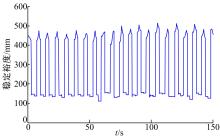
图14为机器人在整个行走过程中的稳定裕度。由图14可以看出, 机器人在整个行走过程中始终具有较大的稳定裕度, 有效地保证了机器人稳定地通过复杂地形。

	Figure Option View Download New Window
	图14 机器人在行走过程中的绝对稳定裕度Fig.14 Absolute stability margin of robot during walking process

图15为机器人躯干沿前进方向(x)和侧方向(y)上的速度和加速度变化曲线。其中, 速度和加速度为零的部分为四足机器人的迈步阶段。

由图15可以看出, 四足机器人在运动过程中, 其躯干运动的加速度和速度都是连续的。这样就可以避免四足机器人在行走过程中, 因自身运动的不连续而产生速度或者加速度的突变, 进而导致破坏机器人稳定性的情况发生。

	Figure Option View Download New Window
	图15 机器人在行走过程中的速度和加速度变化Fig.15 Velocity and acceleration variation curve of robot's body during quadruped robot walking process

图16为机器人行走过程中俯仰角变化曲线, 其中虚线表示的是图10所示崎岖地形的地形起伏。当机器人行走时, 机器人能够根据地形的起伏, 自主调整躯干的俯仰角, 增加摆动足的有效工作空间, 能够使机器人跨越更高的障碍物, 从而有效地提高了机器人的环境适应性。

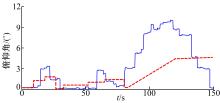	Figure Option View Download New Window
	图16 四足机器人在行走过程中的俯仰角的变化Fig.16 Pitch angle variation curve of robot’ s body during quadruped robot walking process

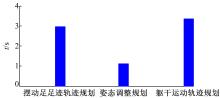
为验证算法的实时性, 将本文算法所包括的姿态调整规划、躯干运动轨迹规划以及摆动足足底轨迹规划, 在CPU型号为Intel Core I3的计算机上使用Matlab各运行一万次, 所用时间如图17所示。由图17可以看出, 本文提出的静步态规划中每部分运行一万次所用的时间均小于4 s, 即单个规划周期均小于0.4 ms。因而本文提出的四足机器人静步态规划方法能够保证四足机器人在崎岖地形上行走时实时地规划其自身运动。

	Figure Option View Download New Window
	图17 静步态规划算法在Matlab中运行一万次所用时间Fig.17 Time required for running algorithms of static gait planning ten thousand times in Matlab

4 结束语

本文通过对四足机器人静步态进行规划, 提高了四足机器人在复杂地形中的通过能力。使用五次曲线规划的重心摆动轨迹, 能够有效地保证机器人运动的连续性并且在整个前行过程中拥有足够的稳定裕度; 通过机器人姿态的调整, 机器人能够跨越更高的障碍物, 从而使机器人能够行走在更加崎岖的地形上。使用本文提出的摆动足足底轨迹规划方法, 机器人能够在无法获取地形信息的情况下, 顺利通过未知的复杂地形环境。仿真实验表明了本文静步态规划方法的有效性, 为提高机器人的环境适应性打下了较好的理论基础。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	Rong Xue-wen, Li Yi-bin, Ruan Jiu-hong, et al. Design and simulation for a hydraulic actuated quadruped robot[J]. Journal of Mechanical Science and Technology, 2012, 26(4): 1171-1177. [本文引用:1]
[2]	McGhee Robert B, Frank Andrew A. On the stabil-ity properties of quadruped creeping gaits[J]. Mathematical Biosciences, 1968, 3: 331-351. [本文引用:2]
[3]	Lee Tsu-tian, Shih Ching-long. A study of the gait control of a quadruped walking vehicle[J]. Robot-ics and Automation, 1986, 2(2): 61-69. [本文引用:3]
[4]	Dimitris Pongas, Mistry Michael, Schaal Stefan. A robust quadruped walking gait for traversing rough terrain[C]∥Proceedings of the IEEE International Conference on Robotics and Automation, Roma, Italy, 2007: 1474-1479. [本文引用:2]
[5]	Buchli Jonas, Kalakrishnan Mrinal, Mistry Michael, et al. Compliant quadruped locomotion over rough terrain[C]∥Proceedings of the IEEE International Conference on Intelligent Robots and Systems, St. Louis, USA, 2009: 814-820. [本文引用:3]
[6]	Kalakrishnan Mrinal, Buchli Jonas, Pastor Peter, et al. Fast, robust quadruped locomotion over challenging terrain[C]∥Proceedings of the IEEE International Conference on Robotics and Automation, Anchorage, Alaska, USA, 2010: 2665-2670. [本文引用:1]
[7]	Zico Kolter J, Rodgers Mike P, Ng Andrew Y. A control architecture for quadruped locomotion over rough terrain[C]∥Proceedings of the IEEE Inter-national Conference on Robotics and Automation, Pasadena, CA, USA, 2008: 811-818. [本文引用:2]
[8]	黄博, 赵建文, 孙立宁. 基于静平衡的四足机器人直行与楼梯爬越步态[J]. 机器人, 2010, 32(2): 226-232. Huang Bo, Zhao Jian-wen, Sun Li-ning. Straight walking and stair climbing gait of quadruped robot based on static balance[J]. Robot, 2010, 32(2): 226-232. [本文引用:2]
[9]	王鹏飞. 四足机器人稳定行走规划及控制技术研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2007. Wang Peng-fei. Research on quadruped robot steadily walking planning and controlling technology[D]. Harbin: School of Mechanical and Electrical Engineering, Harbin Institute of Technology, 2007. [本文引用:3]
[10]	冯华山, 王润孝, 赵国斌, 等. 四足机器人坡面静步态平衡方法研究[J]. 机械科学与技术, 2009, 28(4): 436-441. Feng Hua-shan, Wang Run-xiao, Zhao Guo-bin, et al. A balance method for the static gait of a quadruped robot over a slope[J]. Mechanical Science and Tech-nology for Aerospace Engineering, 2009, 28(4): 436-441. [本文引用:2]
[11]	高杉. 四足机器人静态全方位步行的稳定性研究及实验仿真[D]. 青岛: 中国海洋大学工程学院, 2008. Gao Shan. The study of stability in omnidirectional static walking of a quadruped robot and the simulation[D]. Qingdao: College of Engineering, Ocean University of China, 2008. [本文引用:2]
[12]	de Santos P G, Garcia E, Estremera J. Quadru-pedal Locomotion: an Introduction to the Control of Four-legged Robots[M]. London: Springer, 2007: 59-60. [本文引用:1]
[13]	Shin-Min Song, Waldron Kenneth J. An analytical approach for gait study and its applications on wave gaits[J]. International Journal of Robotics Research, 1987, 6(2): 60-71. [本文引用:1]
[14]	Joaquin Estremera, de Santos Pablo Gonzalez. Generating continuous free crab gaits for quadruped robots on irregular terrain[J]. IEEE Transactions on Robotics, 2005, 21(6): 1067-1076. [本文引用:1]
[15]	Messuri D, Klein Charles A. Automatic body regulation for maintaining stability of a legged vehicle during rough-terrain locomotion[J]. IEEE Journal of Robotics and Automation, 1985, 1(3): 132-141. [本文引用:1]
[16]	Havoutis Ioannis, Ortiz Jesus, Bazeille stéphane, et al. Onboard perception-based trotting and crawling with the hydraulic quadru-ped robot (HyQ)[C]∥Intelligent Robots and Systems (IROS), Tokyo Big Sight, Japan, 2013: 6052-6057. [本文引用:1]

2012

0.0

... 0 引言四足机器人能够在崎岖度较高,甚至是一些对于轮式和履带式机器人无法跨越的复杂地形上行走^[1] ...

1968

0.0

... 在静步态研究方面,McGhee等^[2]首先给出了四足机器人静步态的数学描述 ...

... 2 机器人的静步态迈步顺序对于四足机器人而言,共有6种非奇异的静步态迈步顺序^[2],在这6种迈步顺序中,4-2-3-1为稳定裕度最优的迈步顺序^[12],其中,机器人足的编号如图2所示 ...

1986

0.0

... 其中,比较典型的有:Lee等^[3]提出的静步态规划方法,并详细分析了机器人使用静步态行走时的稳定性 ...

... 现有的四足机器人静步态规划中,有的只规划了机器人躯干在前进方向上的运动^{[3,8,9,10,11]},这种情况下,机器人在行走过程中稳定裕度相对较小 ...

... 有的没有结合姿态调整和足底轨迹规划以提高机器人跨越复杂地形的能力^[3,5,9] ...

2007

0.0

... 机器人进行的相关静步态规划^[4,5,6,7] ...

... 有的虽然增加了侧向移动但是不能保证机器人的重心一直向前运动^[4],降低了机器人的平均运动速度和能量利用效率 ...

2009

0.0

... 机器人进行的相关静步态规划^[4,5,6,7] ...

... 有的没有结合姿态调整和足底轨迹规划以提高机器人跨越复杂地形的能力^[3,5,9] ...

... 但是,由于S_min的存在,使得位于躯干左右两侧足所对应的稳定区域是不连续的^[5] ...

2010

0.0

... 机器人进行的相关静步态规划^[4,5,6,7] ...

2008

0.0

... 机器人进行的相关静步态规划^[4,5,6,7] ...

... 四足机器人在摆动不同的足时所对应的支撑三角形是不同的,但是位于身体同侧的足所对应的支撑三角形存在重合的区域,这个重合区域被称为双支撑三角形(Double support triangle)^[7] ...

2010

0.0

. 2010, 32(2):226-232

Straight walking and stair climbing gait of quadruped robot based on static balance

基于静平衡的四足机器人直行与楼梯爬越步态

Huang Bo , Zhao Jian-wen , Sun Li-ning.

黄博, 赵建文, 孙立宁

To improve obstacle climbing performance of the quadruped robot, stability margin is selected as the criterion of quadruped static balance, and quadrant boundary formed by touchdown points is taken as the stride possibility criterion in various initial conditions. All gaits are classified into 24 types by stride sequences. Based on the evaluation guidelines including minimal locomotion space demand, maximal stability margin, and best body adjustment coordination, contrast analyses on all 24 basic gaits are performed. Furthermore, a projection method combined with planar statically balanced gait theory is proposed to solve stair climbing gait problem, and systematic simulation of stair climbing gait is implemented to meet the 3 evaluation guidelines mentioned above. The simulation results provide theoretical foundation for selecting quadruped walking and stair climbing gaits. Experiments testify the validity of this method.

为提升四足机器人的障碍爬越能力，采用稳定裕度作为四足机器人静态稳定的判据，以落足点形成的象限边界明确了不同初始位姿机器人的迈腿可能性．基于迈腿次序将所有步态划分为24种类型．利用运动空间需求最小、稳定裕度最大、步态协调性最好3个基本评价指标，对四足机器人的24种基本步态进行了对比分析．提出了基于投影分析法结合平面静平衡步态理论的楼梯爬越步态研究方法，并以上述3个特性参数最佳为要求，对楼梯爬越步态进行了系统仿真，所得结果为四足机器人的直行与楼梯爬越步态选择提供了理论依据．实验表明了所研究方法的有效性．

... 黄博等^[8]对机器人爬越楼梯时的静步态进行了规划 ...

... 现有的四足机器人静步态规划中,有的只规划了机器人躯干在前进方向上的运动^{[3,8,9,10,11]},这种情况下,机器人在行走过程中稳定裕度相对较小 ...

2007

0.0

. 2007, :-

Research on quadruped robot steadily walking planning and controlling technology

四足机器人稳定行走规划及控制技术研究

Wang Peng-fei.

王鹏飞

在地球陆地表面，有超过50％以上的面积为崎岖不平的山丘或沼泽，仅仅依靠轮式机械无法完全实现在这些自然环境中的移动。因此，设计和制造一个类似动物能够在自然环境中步行的机器，一直以来是人类追求的目标。正是这个原因，使得仿生足式机器人的研究成为机器人研究领域的热点之一。其中四足机器人由于其既有超于二足机器人的平稳性又避免了六足机器人机构的冗余和复杂性，在工程探险、反恐防爆、军事侦察等具有良好的应用前景，开展该方面的研究具有重要的实际应用价值及社会意义。　　本课题所研究的对象为足轮混合式四足机器人，其能很好的结合轮式机...

... 王鹏飞^[9]根据机器人在迈步阶段躯干是否移动,将四足机器人的静步态分为间歇爬行步态和连续爬行步态,并对这两种步态的稳定性等方面进行了规划和分析 ...

... 现有的四足机器人静步态规划中,有的只规划了机器人躯干在前进方向上的运动^{[3,8,9,10,11]},这种情况下,机器人在行走过程中稳定裕度相对较小 ...

... 有的没有结合姿态调整和足底轨迹规划以提高机器人跨越复杂地形的能力^[3,5,9] ...

2009

0.0

. 2009, 28(4):436-441

A balance method for the static gait of a quadruped robot over a slope

四足机器人坡面静步态平衡方法研究

Feng Hua-shan , Wang Run-xiao , Zhao Guo-bin

冯华山, 王润孝, 赵国斌

着重分析了四足机器人在坡面行走的过渡状态下姿态的平移、俯仰和滚转变化情况。建立了微冲击足尖轨迹模型,消除了机器人坡面行走的平移滑动。采用经滤波处理的姿态反馈角度对中位点各参数进行连续调节,实现过渡状态下对姿态在纵向和横向上的倾斜补偿。提出了利用姿态角反馈形成对角腿弯曲平衡方法,以动态方式稳定坡面行走姿态。试验表明: 四足机器人采用该方法能够稳定实现过渡状态下的坡面行走。

... 冯华山等^[10]对四足机器人在坡面静步态平衡方法进行了相关的研究,着重分析了四足机器人在坡面行走的过渡状态下姿态的变化情况以及稳定行走的方法 ...

... 现有的四足机器人静步态规划中,有的只规划了机器人躯干在前进方向上的运动^{[3,8,9,10,11]},这种情况下,机器人在行走过程中稳定裕度相对较小 ...

2008

0.0

. 2008, :- DOI:doi:10.7666/d.y1336877

The study of stability in omnidirectional static walking of a quadruped robot and the simulation

四足机器人静态全方位步行的稳定性研究及实验仿真

Gao Shan.

高杉

多足型机器人相对于轮形机器人有着很高的地形环境适应能力，可以在复杂地形进行全方位的移动，因此广泛应用于救灾，以及工程等领域。四足机器人又是多足机器人中最实用的一种，在复杂地面进行移动时，静步态移动方式稳定性较好。目前的四足机器人静态全方位步行理论研究中，通过连续步态迁移的方法实现了四足机器人在平面上静态全方位步行的运动方式。但是在四足机器人静态全方位步行的实验中，发现在占空比β=0.75没有四脚支持时间的运动方式下，在步态迁移的过程中，四足机器人经常出现倾倒的现象。本文基于以前的四足机器人静态全方位理论，进行了...

... 高彬^[11]对四足机器人使用静步态进行全方位转向做了相关研究 ...

... 现有的四足机器人静步态规划中,有的只规划了机器人躯干在前进方向上的运动^{[3,8,9,10,11]},这种情况下,机器人在行走过程中稳定裕度相对较小 ...

2007

0.0

1987

0.0

... 为了准确而有效地衡量机器人的静态稳定性,目前存在多种稳定裕度的计算方法,例如纵向稳定裕度(Longitudinal stability margin)^[13]、绝对稳定裕度(Absolute stability margin)^[14]、能量稳定裕度(Energy stability margin)^[15]等 ...

2005

0.0

1985

0.0

2013

0.0

... 2 躯干运动轨迹规划本文是以非连续静步态为基础进行规划的,当机器人在足的摆动阶段,其躯干静止不动,这样能够避免出现机器人在迈步阶段因足底滑动而失去稳定性的情况^[16] ...