仿人头颈部机器人跟踪运动控制

引用本文

祁若龙, 张伟, 王铁军, 李正. 仿人头颈部机器人跟踪运动控制. 2016, 46(5): 1595-1601
QI Ruo-long, ZHANG Wei, WANG Tie-jun, LI Zheng. Tracking motion control method of humanoid head and neck robot. Journal of Jilin University Engineering and Technology Edition, 2016, 46(5): 1595-1601 复制到剪切板

Permissions

仿人头颈部机器人跟踪运动控制

祁若龙^1,², 张伟¹, 王铁军¹, 李正¹

1.中国科学院沈阳自动化研究所机器人学国家重点实验室,沈阳 110016

2.中国科学院大学,北京 100049

作者简介:祁若龙(1983-),男,副研究员,博士研究生.研究方向:机器人自主控制.E-mail:qiruolong@sia.cn

基金:国家自然科学基金项目(51505471); “863”国家高技术研究发展计划项目(2015AA7026090)

摘要

仿人头颈部机器人是仿人机器人的一部分,负责对视觉目标进行动态跟踪。为了能够精确跟踪目标,在系统运动学建模过程中,将机器人视场中心的视线作为一个具有伸缩自由度的连杆加入头颈部结构的运动学模型。通过双目视觉系统计算得到的目标点位置在数学模型上成为连杆机构运动的目标位置。为了使具有冗余自由度的头颈部机器人的运动更符合人类的动作行为,对用于消除运动学奇异点的阻尼最小二乘逆解算法进行了改进。改进后的修正算法不仅能够使机器人在运动过程中避开奇异点,而且能够实现算法上的关节限位,保证机器人运动的关节舒适度,使其更符合人类的行为习惯。仿真实验表明:这种算法在很大程度上提高了机器人运动的可靠性和稳定性。

关键词: 自动控制技术; 冗余机械臂; 阻尼最小二乘法; 虚拟连杆; 关节限位; 关节舒适度

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2016)05-1595-07

Tracking motion control method of humanoid head and neck robot

QI Ruo-long^1,², ZHANG Wei¹, WANG Tie-jun¹, LI Zheng¹

1.The State Key Laboratory of Robotics, Shenyang Institute of Automation, Chinese Academy of Sciences,Shenyang 110016,China

2.University of Chinese Academy of Sciences,Beijing 100049, China

Abstract

Humanoid head and neck robot, which is part of humanoid robot, is responsible for dynamic visual target tracking. In order to be able to accurately track the target, the centre of the robot's sight field serves as stretch link in the kinematics model of the humanoid head and neck robot. The target position calculated by the binocular camera system is translated to the aim point, where the link mechanism moves to in the mathematic model. Damped least squares inverse kinematics method, which is used to eliminated the joint singularity, is modified to make the redundant humanoid head and neck robot moves like human being. The modified algorithm not only makes the robot to avoid the singularity in the movement, but also guarantees joint limit avoidance, comfortable joint movement and produces natural-looking postures. Simulation and experiment results show that the modified algorithm is more robust and stable.

Keyword: automatic control technology; redundant manipulator; damped least squares method; virtual links; joint limits; joint comfortable criteria

Show Figures

0 引言

目前世界各国将仿人机器人的研究作为机器人领域的重点方向之一^[1]。仿人机器人的头颈部视觉跟踪系统需要具有偏摆和俯仰两个自由度以便对移动物体进行动态跟踪^[2]。但出于结构相似性和前向视觉的灵活性需要, 仿人机器人的头颈部一般采用冗余自由度的设计。这也给仿人机器人头颈部的运动控制带来了挑战:①如何建立相机测得的被跟踪物体空间位置和头部运动之间的联系。传统的视觉跟踪系统多采用类似云台的两关节轴心相交的万向节构型, 其视觉空间是一个完整的球体, 可以通过球面投影的方式计算两个运动关节的偏角^[3]。但这种方法并不适用于关节轴不正交的冗余自由度头颈部机器人的运动控制。②由于机器人具有冗余自由度, 理论上可以有无穷多个姿态观测一个固定点, 如何能够以最接近人类自然行为的姿态“ 优雅” 地运动是尚待解决的问题。③在冗余自由度机构运动的时候, 如何能够通过各自由度之间的相互补充协调, 使各自由度在运动中尽量避开关节极限位置。通常一般系统中采用软限位的方法进行限位, 在系统算法计算得到的关节角大于极限位置的情况下只给定极限位置的控制信号, 这种方法带来的后果是末端产生不可预知的轨迹偏差, 导致视觉跟踪和控制失败^[4]。④需要在算法内部同时保证避开关节奇异点, 以避免机构产生突然的大幅度异常运动。

Zhang等^[5]在研究中赋予了人形机器人头部俯仰、偏摆2个自由度, 建立了面部的虚拟平面, 推导视觉目标和两个关节角关系的二次方程, 并采用神经网络算法进行求解。Bie等^[6]针对两自由度关节轴正交的机器人头部, 建立球面上的目标点和关节转角关系, 并直接采用视觉目标空间位置和关节PID闭环控制机制进行视觉伺服控制。Hirth等^[7]将机器人头部的动作进行归类, 采用人工智能的方法定义机器人的行为习惯。Omr $\begin{matrix} \overset{ˇ}{c} \end{matrix}$ en等^[8]的研究对象是一个眼睛能够分别转动的5自由度机器人头部, 为了解决两只眼睛观测同一物体时的角度差异, 对两只眼睛分别进行了冗余自由度机器人的建模然后连立在一起。Giulio^[9]与Omr $\begin{matrix} \overset{ˇ}{c} \end{matrix}$ en的研究对象相同, 为了使带有冗余自由度的机器人头部能够稳定地运动, 在逆解算法之前引入Kalman滤波对目标位置进行预测。王丽佳^[10]等在目标物体视觉跟踪的研究中, 采用改进Mean-shift算法对物体进行粗、精两次定位保证跟踪精度。在仿人机器人头部运动控制的研究中基本上可以分为两种实现手段:一种是从机械上简化机构以获得稳定、简单的控制优势; 另一种是冗余化的多自由度机械结构, 建立复杂的跟踪方程或智能化的控制策略, 借助滤波估计等手段提高算法稳定性, 但在一定程度上牺牲了算法周期计算的实时性。

本文将机器人视觉跟踪问题通过“ 虚拟连杆” 的建立转化为冗余自由度机器人的运动控制问题。对阻尼最小二乘法进行改进, 引入关节限定系数和关节权重因子, 能够同时满足避开运动学奇异点、远离限位和尽可能在预先定义的舒适关节角度附近工作的需要, 且计算量较小, 能够满足100 Hz近似人类应激频率的高频伺服控制需要。

1 虚拟连杆与模型建立

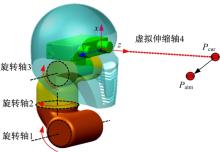
由中国科学院沈阳自动化研究所研制的仿人头颈部机器人如图1所示。

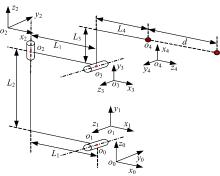
	Figure Option View Download New Window
	图1 仿人头颈部机器人示意图Fig.1 Sketch map of humanoid head and neck robot

机器人两只眼睛的中间位置是相机的基坐标系, 机器人本体具有3个转动轴。从几何角度分析, 机器人三个转动自由度能够确定一条与相机基坐标系z轴重合的射线, 但是由于机械结构上三个转动轴的轴心不相交于一点, 因此这些射线并不是从同一个原点向外散射的, 是互相相交的, 理论上通过仿人机器人头部视觉范围内的某一点可以有无数条这样的射线, 也就是说机器人观察某一点时可以有无数个姿态。这与人转动脖颈可从不同角度观察空间某一点的特性是一致的。当人的视线没有改变的情况下, 视线上的一个点(可以想象成乒乓球)向人沿视线方向靠近, 人不需要移动视线, 只调节眼睛的焦距就能够一直观察物体。视觉相机的焦距是一个范围, 因此, 从精确观测物体的角度, 建立从相机基坐标系原点到被测物体之间的虚拟连杆, 能够表达空间一点位置和机器人各轴角度之间的关系。仿人头颈部机器人的连杆和坐标系如图2所示, DH参数如表1所示。

	Figure Option View Download New Window
	图2 机器人连杆坐标系Fig.2 Connecting rod coordinate of robot

表1 仿人头颈部机器人DH参数表 Table 1 DH parameters of humanoid head and neck robot

2 算法实现

2.1 阻尼最小二乘法

选择仿人头颈部机器人的关节1中心作为空间笛卡尔坐标系的原点和机器人的坐标系的原点。当前周期机器人各关节轴位置φ =(θ ₁, θ ₂, θ ₃, d), 对应的视线虚拟连杆末端空间位置为P_cur=(x_cur, y_cur, z_cur)^T, 本周期视觉相机测得的目标点位置为P_aim=(x_aim, y_aim, z_aim)^T, 则

$\begin{matrix} \begin{matrix} E = P_{aim} - P_{cur} = JΔφ (1) \\ Δφ = J^{- 1} E (2) \end{matrix} \end{matrix}$

式中:J为雅克比矩阵, 是机器人视觉虚拟连杆末端在空间笛卡尔坐标系下运动速度相对于关节速度的比值。

通过式(2)计算得到的关节位置增量Δ φ 为本周期得到的控制量, 发送给关节驱动器执行。但由于式(2)直接求雅克比矩阵的广义逆, 在机构奇异点的位置雅克比矩阵是矩阵的秩不为零的病态矩阵, 得到的关节角度增量是错误的。

为避开奇异点, Nakamura^[11]和Wampler^[12]分别建议在运动学逆解求取时采用阻尼最小二乘技术, 求取满足式(3)的角度增量最小解。

$\begin{matrix} ‖ JΔθ - E ‖^{2} + λ^{2} ‖Δ θ ‖^{2} (3) \end{matrix}$

式中:λ ∈ R为阻尼系数, 能够满足式(3)获得最小值的Δ θ 为:

$\begin{matrix} Δθ = (J^{T} J + λ^{2} {I)}^{- 1} J^{T} E (4) \end{matrix}$

2.2 改进阻尼最小二乘法

2.2.1 舒适限位系数

对于具有n个自由度的机器人, 阻尼系数λ 是一个n阶对角阵。

$\begin{matrix} λ = diag (λ_{i}) = (\begin{matrix} λ_{1} \\ ⋱ \\ λ_{n} \end{matrix}) (5) \end{matrix}$

式中:λ _i对应于对第i个关节的控制, λ _i的值越大, 对应的关节“ 阻抗” 越高, 灵活度越差。当机器人关节接近极限位置时, 希望关节的阻抗增大, 在关节越舒适的位置, 希望关节阻抗越小。随着机器人运动关节位置值的变化, λ 的值实时改变, 在使机器人关节远离限位的同时尽可能接近关节舒适位置, 因此称λ 为“ 舒适限位系数” 矩阵。采用分段函数定义舒适限位系数:

$\begin{matrix} λ_{i} = \{\begin{matrix} μ {[\frac{θ_{i} - θ_{icomf}}{θ_{\max} - θ_{icomf}}]}^{P}, \begin{matrix} θ_{i} \geq θ_{icomf} \end{matrix} \\ μ {[\frac{θ_{icomf} - θ_{i}}{θ_{icomf} - θ_{\min}}]}^{P}, \begin{matrix} θ_{i} < θ_{icomf} \end{matrix} \end{matrix} (6) \end{matrix}$

式中:μ , P∈ R⁺, μ 为关节阻抗参数, P为关节灵活度参数, P为偶数, 它们是可根据实验和仿真情况调节的常量; θ _i_comf为设定的关节最舒适位置, 对于机械臂的某一个末端位置, 算法在计算过程中会使各关节的角度自动趋近于θ _i_comf。

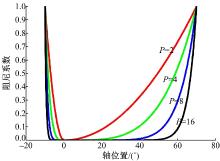
设关节i角度极限位置值为θ _i_max=10° , θ _i_min=-70° , 关节在0° 处最为舒适。关节运动范围内μ =1, P=2、4、8、16时阻抗曲线如图3所示。在机械臂等研究中, 当不需要刻意强调关节舒适位置时, 可以令:

$\begin{matrix} θ_{icomf} = (θ_{imax} + θ_{imin} \frac{)}{2} \end{matrix}$

此时, 式(6)不需要分段, 退化为:

$\begin{matrix} λ_{i} = μ {[\frac{2 θ_{i} - θ_{imax} - θ_{imin}}{θ_{imax} - θ_{imin}}]}^{P} (7) \end{matrix}$

实际应用中P值主要影响关节接近限位时的阻抗, μ 值影响关节灵活度, 在冗余自由度机械臂的控制中, 在多个关节以不同的方式相互配合运动都能够实现同样的等效末端运动时, μ 值小的关节相对于μ 值较大的关节更容易产生运动。

	Figure Option View Download New Window
	图3 阻尼系数曲线Fig.3 Curves of damping factor

2.2.2 关节权重

式(6)在θ _i=θ _i_comf时, λ _i=0, 如果此时恰巧机器人关节在奇异点附近, 依然能产生病态解。因此, 在式(6)中增加关节权重系数:

λ _i= $\begin{matrix} \{\begin{matrix} μ {[\frac{θ_{i} - θ_{icomf}}{θ_{\max} - θ_{icomf}}]}^{P} + ω_{i}, \begin{matrix} θ_{i} \geq θ_{icomf} \end{matrix} \\ μ {[\frac{θ_{icomf} - θ_{i}}{θ_{icomf} - θ_{\min}}]}^{P} + ω_{i}, \begin{matrix} θ_{i} < θ_{icomf} \end{matrix} \end{matrix} \end{matrix}$ (8)

式中:0< ω _i< 1, 关节权重一方面能够同μ 值一起对关节运动灵活度产生作用, 另一方面ω _i的存在能够消除结构奇异点的影响, 保证雅克比矩阵的满秩。实际中建议ω _i在[0.01, 0.1]中取值。

3 仿真实验

本文所述方法在Matlab和VC平台下进行了仿真验证。Matlab仿真在本项目中用于算法有效性的对比验证和参数选择, VC平台用于工程实际应用。仿人头部机器人的关节参数如表2所示。

表2 关节参数 Table 2 Joint parameters

3.1 Matlab仿真

为了验证算法的合理性, 移动各轴位置, 使机器人各轴处于(30° , -35° , 103° , 180 mm)处, 此时机器人末端空间位置为(266.9, -186.3, 42.9)(单位为mm), 作为运动的起始点。移动机器人使机器人各轴位于(-8° , 35° , 82° , 20 mm)处, 此时机器人末端空间位置为(29.4, 83.36, 250.7)(单位为mm), 作为运动的目的点。这样进行设置的目的是, 一方面确定机器人末端沿起始点和目的点的直线路径上不存在不可达空间, 另一方面在目的点附近, 关节1和关节3两个运动量较小的关节都在极限位置附近, 从而考验算法稳定性。

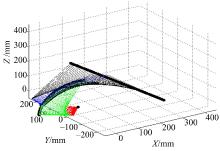
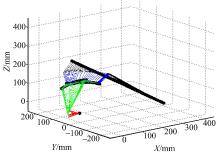
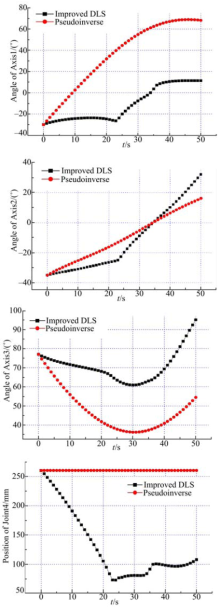
广义逆方法的机器人连杆运动示意图如图4所示, 本文算法的仿真连杆示意图如图5所示。两种算法以同样的末端起始点、终止点和相同的50 s运行时间运动, 过程中关节位置对比如图6所示。普通广义逆的方法由于各关节的逆解计算过程缺乏约束, 关节1达到75° , 极大地超过了关节1的正向极限位置15° , 关节3达到37° , 也超过了60° 的关节负限位值。通过本文所述的改进阻尼最小二乘法, 机器人各运动轴位置没有超过限位, 颈部(图4、图5中绿色部分)倾角一直较小, 保持在设置的舒适角度附近, 这会使机器人头部动作看起来更符合人的行为习惯。

	Figure Option View Download New Window
	图4 广义逆法的机器人运动示意图Fig.4 Sketch map of robot movement by pseudoinverse method

	Figure Option View Download New Window
	图5 改进阻尼最小二乘法机器人运动示意图Fig.5 Sketch map of robot movement by improved DLS method

	Figure Option View Download New Window
	图6 关节运动参数对比Fig.6 Comparison of joint movement

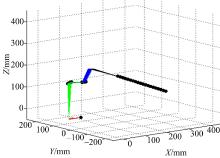
为了测试本文提出的用于表征视线变焦的伸缩连杆性能, 任意选取两个关节角度相同的观测姿态(-5° , -20° , 110° , 300 mm)和(-5° , -20° , 110° , 20 mm)作为机器人观测末端点的起始和终止位置。也就是说, 机器人最理想的观测行为是在末端平移的过程中关节角保持不变, 只有伸缩连杆发生长度变化。根据本文所述方法, 机器人的观测过程如图7所示。

	Figure Option View Download New Window
	图7 虚拟连杆伸缩测试Fig.7 Simulation comparison on VC platform

机器人到达末端点各关节值约为(-1° , -16° , 116° , 34.5 mm), 三个转动关节分别只移动了4° 、5° 和4° , 而伸缩连杆移动了266.5 mm。机器人在头部姿势只有很小变化量的情况下, 跟踪了在视线方向上变化量很大的物体。由此可知, 本文提出的虚拟连杆在视觉跟踪应用方面的有效性。

3.2 VC仿真

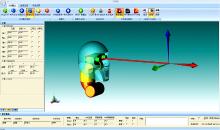
VC平台下头颈部机器人更加逼真, 不仅能够更直观地观察仿真状态, 而且可以应用于对机器人的实际控制。基于C++语言的机器人仿真平台构建方法可以参考文献[13]。仿真平台如图8所示。

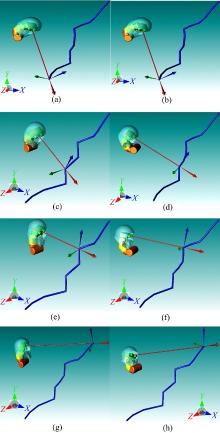
	Figure Option View Download New Window
	图8 仿人头颈部机器人VC仿真平台Fig.8 VC simulation platform of humanoid head and neck robot

在仿真平台下, 任意定义一条空间样条曲线, 作为机器人的视觉目标轨迹。对比广义逆算法和本文所述改进阻尼最小二乘法的运动过程, 可以直观地感受不同算法对头颈部机器人跟踪姿态的影响。VC仿真对比如图9所示, 图9(a)(c)(e)(g)为改进阻尼最小二乘法的机器人跟踪过程采样, 图9(b)(d)(f)(h)为广义逆法的跟踪过程采样。

	Figure Option View Download New Window
	图9 VC平台仿真对比Fig.9 Simulation comparison on VC platform

通过仿真对比可见, 图9(b)(d)(f)(h)在没有改进阻尼最小二乘约束的情况下, 仿人头颈部机器人的运动是一种能够使机器人末端处于目标位置的肆意关节角度。从VC仿真平台上可以清楚地看到, 机器人的面具与自己的颈部发生了干涉, 并且机器人的头部姿势处于一种不同于人类行为的姿态, 这在机器人的实际应用中是不可以接受的。而图9(a)(c)(e)(g)由于改进阻尼最小二乘法的应用, 机器人能够在保证跟踪目标位置的前提下, 尽量使运动幅度最小、关节角在人类头部直立的角度附近运动, 从而实现了对人类头部视觉跟踪运动的仿生。

4 结束语

通过改进阻尼最小二乘法, 在冗余自由度机器人逆解过程中添加了关节运动的约束。通过这种方法机器人不仅能够实现对关节的限位和避开奇异点, 而且可以通过设置舒适关节角度使机器人的运动能够尽可能地保持在舒适关节角度附近, 从而实现了对人类行为习惯的仿生。还需要说明的有如下两点:

(1)在一般具有冗余自由度的工业机器人的控制中, 由于并不关注机器人的关节行为, 这种方法的优势可能并不突出。但在仿人手臂的仿生运动研究中可以和本文一样通过设置关节舒适度函数, 使机器人的手臂运动与人类运动习惯近似。或者太空、水下等能量资源比较珍贵的环境下, 可以通过本文的方法设置关节权重, 降低机械臂根部承受较大扭矩关节的灵活度, 以节省能量和减小较大、较重连杆关节运动幅度, 降低运动风险。

(2)冗余自由度的广义逆方法的本质在数学上是一种梯度下降法, N个关节角在N维空间中有无数条路径使机器人从一个末端位姿到达另一个末端位姿。广义逆的方法选择了梯度下降最快的方式, 具有单步总关节角度变化量最小的优势, 但在具有伸缩自由度连杆的情况下, 与连杆长度变化相比, 旋转关节可以通过较小角度的旋转使末端产生较大的运动, 从而比移动关节更具优势, 因此广义逆方法在计算中, 移动关节一般灵活度不高。广义逆算法总在用关节旋转产生的末端位移替代连杆伸缩产生的末端位移。因此本文方法可以应用在具有移动连杆的冗余自由度机器人中, 使移动连杆有效参与运动。

仿真实验表明本文所述方法简单实用, 能够稳定、可靠地应用于工程实践。

The authors have declared that no competing interests exist.

参考文献

View Option

[1]	于秀丽, 魏世民, 廖启征. 仿人机器人发展及其技术探索[J]. 机械工程学报, 2009, 45(3): 71-75. Yu Xiu-li, Wei Shi-min, Liao Qi-zheng. Development and technology research of humanoid robot[J]. Journal of Mechanical Engineering, 2009, 45(3): 71-75. [本文引用:1]
[2]	李允明. 国外仿人机器人发展概况[J]. 机器人, 2005, 27(6): 561-567. Li Yun-ming. Foreign status of humanoid robot[J]. Robot, 2005, 27(6): 561-567. [本文引用:1]
[3]	孙鹏飞, 郭喜庆, 杨敬娴. 二自由度云台的机器视觉控制[J]. 光电工程, 2012, 39(10): 135-142. Sun Peng-fei, Guo Xi-qing, Yang Jing-xian. Controlling of 2-DOF PZT with machine vision[J]. Opto-Electronic Engineering, 2012, 39(10): 135-142. [本文引用:1]
[4]	周扬. 双臂机器人的控制系统建立及阻抗控制研究[D]. 哈尔滨: 哈尔滨工业大学机电工程学院, 2014. Zhou Yang. Establishment of control system and research on impedance control for dual-arm robots[D]. Harbin: School of Mecharonics Engineering, Harbin Institute of Technology, 2014. [本文引用:1]
[5]	Zhang Z, Beck A, Magnenat-Thalmann N. Human-like behavior generation based on head-arms model for robot tracking external targets and body parts[J]. IEEE Transactions on Cybernetics, 2015, 45(8): 1390-1400. [本文引用:1]
[6]	Bie Hai-gang, Huang Qiang, Zhang Wei-min, et al. Visual tracking of a moving object of a robot head with 3 DOF[C]∥International Conference on Rohotics, lntelligent Systems and Signal Processing, Changsha, China, 2003: 686-691. [本文引用:1]
[7]	Hirth J, Berns K. Concept for behavior generation for the humanoid robot head ROMAN based on habits of interaction[C]∥Proc of the 7th IEEE-RAS International Conference on Humanoid Robots, Pennsylvania, USA, 2007: 360-365. [本文引用:1]
[8]	Omrcen D, Ude A. Redundant control of a humanoid robot head with foveated vision for object tracking[C]∥2010 IEEE International Conference on Robotics and Automation, Anchorage, USA, 2010: 4151-4156. [本文引用:1]
[9]	Giulio M, Luca V, Alessand ro D L. Adaptive predictive gaze control of a redundant humanoid robot head[C]∥2011 IEEE/RSJ International Conference on Intelligent Robots and Systems, San Francisco, USA, 2011: 3192-3198. [本文引用:1]
[10]	王丽佳, 贾松敏, 王爽, 等. 采用改进Mean Shift算法的移动机器人行人跟踪[J]. 光学精密工程, 2013, 21(9): 2364-2370. Wang Li-jia, Jia Song-min, Wang Shuang, et al. Person tracking of a mobile robot using improved Mean Shift[J]. Optics and Precision Engineering, 2013, 21(9): 2364-2370. [本文引用:1]
[11]	Nakamura Y, Hanafusa H. Inverse kinematic solutions with singularity robustness for robot manipulator control[J]. ASME Journal of Dynamic Systems, Measures & Control, 1986, 108: 163-171. [本文引用:1]
[12]	Wampler C W. Manipulator inverse kinematic solutions based on vector formulations and damped least-squares methods[J]. IEEE Transactions on Systems Man & Cybernetics, 1986, 16(1): 93-101. [本文引用:1]
[13]	祁若龙, 周维佳, 刘金国, 等. VC平台下机器人虚拟运动控制及3D运动仿真的有效实现方法[J]. 机器人, 2013, 35(5) 594-599. Qi Ruo-long, Zhou Wei-jia, Liu Jin-guo, et al. An constructing method of 3D simulation and virtual motion control system in VC platform[J]. Robot, 2013, 35(5): 594-599. [本文引用:1]

2009

0.0

. 2009, 45(3):71-75 DOI:doi:10.3901/JME.2009.03.071

Development and technology research of humanoid robot

仿人机器人发展及其技术探索

Yu Xiu-li , Wei Shi-min , Liao Qi-zheng

于秀丽, 魏世民, 廖启征

仿人机器人是研究人类智能的高级平台,它是综合机械、电子、计算机、传感器、控制技术、人工智能、仿生学等多种学科的复杂智能机械,目前已成为机器人领域的研究热点问题之一.对国内外仿人机器人研究现状进行广泛调研,其中日、美等国在研制仿人机器人方面做了大量的工作,中国各高校也积极研究,取得了突破性进展.概括并分析机器人自由度配置、步态规划的分类、基于零力矩点的稳定性判据、传感器的分类和应用以及机器人控制系统等关键技术.

... 0 引言目前世界各国将仿人机器人的研究作为机器人领域的重点方向之一^[1] ...

2005

0.0

. 2005, 27(6):561-567 DOI:doi:10.3321/j.issn:1002-0446.2005.06.017

Foreign status of humanoid robot

国外仿人机器人发展概况

Li Yun-ming

李允明

The primary techniques and their technical parameters of humanoid robot in Japan,USA and the Republic of Korea are analyzed in detail.Based on the design of foreign sample humanoid,the author discusses the DOF selection of various parts of humanoid robot,analyzes several driving and control issues.The enlightenment to accelerate the development of humanoid robot in China based on overseas development is provided.

介绍了国外仿人机器人发展的特点，详细分析了日本、美国和韩国等国几种仿人机器人的主要技术及其技术指标．根据国外的样机设计，作者讨论了仿人机器人各部分自由度的选用，分析了仿人机器人传动和控制设计中的一些问题．就国外仿人机器人发展对中国的启示提出了看法．

... 仿人机器人的头颈部视觉跟踪系统需要具有偏摆和俯仰两个自由度以便对移动物体进行动态跟踪^[2] ...

2012

0.0

. 2012, 39(10):135-142 DOI:doi:10.3969/j.issn.1003-501X.2012.10.022

Controlling of 2-DOF PZT with machine vision

二自由度云台的机器视觉控制

Sun Peng-fei , Guo Xi-qing , Yang Jing-xian

孙鹏飞, 郭喜庆, 杨敬娴

A vision-controlled model for two Degrees of Freedom (2-DOF) PZT is established, and through the analysis of the tracked object's location on the image planes of adjacent frames taken by the cameras, we realize a high efficiency and time-saved aim surveillance. Alternative functions are taken to depict the input angle that adjusts the PZT to track the moving object. It is found that the deviant brought in by the approximate model can be neglected compared to the accurate model. The location-feedback method improves the efficiency of aim-searching. The results demonstrate that with 25 frames per second, the camera is able to track the object with lower location deviant, compared with the original. Even when the object's speed increases to 2 m/s, it could also stably track the object. A binocular vision model is proposed for the controlling system, and it can avoid the object-loss area during the tracking.

本文建立了基于机器视觉反馈的云台控制模型，并通过相邻帧间的目标位置预测来简化搜索算法，实现快速高效的视觉云台对运动目标的连续跟踪。在制定系统空间转角输入量的控制策略中，简化了控制模型并对产生的偏差量进行了分析。结果表明，简化后的控制算法能够实现快速反馈和像面调整，在25帧/秒时实现对运动目标稳健跟踪，且跟踪精度高于传统算法；在目标速度2 m/s、相机60帧/秒时，改进算法实现了对运动目标的连续跟踪。同时提出了立体视觉系统模型及其在云台控制中的应用，通过像面坐标获取空间位置信息以规避目标跟丢现象。

... 传统的视觉跟踪系统多采用类似云台的两关节轴心相交的万向节构型,其视觉空间是一个完整的球体,可以通过球面投影的方式计算两个运动关节的偏角^[3] ...

2014

0.0

. 2014, :-

Establishment of control system and research on impedance control for dual-arm robots

双臂机器人的控制系统建立及阻抗控制研究

Zhou Yang

周扬

随着双臂机器人特别是具有冗余机械臂的双臂仿人机器人的飞速发展，对机器人在不确定环境（例如与人交互）的鲁棒性提出了更高的要求，因此阻抗控制成为该领域研究的重要方向。本文结合实验室的机器人宇航员预研项目，研制了基于现代化硬件与软件技术的双臂机器人控制系统，开展了具有零空间阻抗的七自由度冗余机械臂阻抗控制，以及面向物体的双臂多空间自适应阻抗控制研究，并利用机器人宇航员实验平台进行了机械臂阻抗控制实验。从双臂机器人控制系统具体软硬件实现角度，本文以机器人宇航员地面实验平台为例分析了双臂机器人系统特点。在此基础上，建立了层次化的双臂机器人控制系统架构，研制了基于EPIC的中央控制器、基于mLVDS的MMSC总线和接口卡、模块化关节控制器、基于1394b的视觉计算机以及程控电源，从而将现代化硬件的计算能力和通信速度灵活地映射到具体的机器人控制系统中，使其具有更加广泛的适用性和强大的实时性。结合控制系统硬件，设计了基于Simulink，具有快速化原型、模块化抽象和标准化通信的控制系统软件。最终实现了可以使用Simulink开发的机器人控制系统，使用户能够快速实现机器人控制算法的实时仿真与实验。从冗余机械臂阻抗控制角度，为了解决具有位置内环的阻抗控制方法不能控制冗余机械臂零空间运动的问题，分析了七自由度冗余机械臂的构型特点，在此基础上引入了柔顺面和臂平面，将这两个平面之间的夹角定义为臂角，以此来描述冗余机械臂的零空间阻抗运动，并根据能量论推导了含有刚度项的零空间阻抗方程，使其表达式具有了明确的物理意义，再将该方程与动力学方程结合，最终提出了具有零空间阻抗的冗余机械臂阻抗控制方法。这种控制方法使七自由度冗余机械臂保留了笛卡尔空间阻抗的同时，实现了零空间阻抗。在基于SimMechanics的七自由度冗余机械臂系统模型上，仿真验证了提出的阻抗控制方法，并与一般的阻抗控制方法进行了比较。比较结果表明，当机械臂受到外界作用力干扰时，这种方法在机械臂的零空间也实现了柔顺行为，同时使笛卡尔空间的位置误差渐进收敛。从冗余机械臂阻抗避障角度，针对一般阻抗控制方法无法实现机械臂避障问题，利用一种虚拟力造成的机械臂自运动来实现自避障。当机械臂靠近障碍物时，作用在机械臂上的虚拟力是由障碍物指向机械臂的一种排斥力。在这种虚拟排斥力的作用下，利用冗余机械臂的零空间阻抗实现了避障，同时完成了机械臂末端的轨迹跟踪。通过仿真验证了该方法的有效性，仿真结果还表明，即使在避障过程中，机械臂末端的位置跟踪精度也没有受到影响。从双臂阻抗控制角度，考虑机械臂夹持物体时，机械臂对物体的作用力容易饱和的问题，从机械臂角度分析了人体运动控制和学习特性。在此基础上引入了面向物体的阻抗作为阻抗控制外环，结合机械臂阻抗作为阻抗控制内环，使物体和机械臂都具有了阻抗特性。并基于能量代价函数提出了物体的阻抗自适应律，利用Lyapimov函数证明了该自适应律能够使能量代价函数趋于最小。通过仿真验证了该方法的有效性，仿真结果表明通过机械臂阻抗和物体阻抗可以减小机械臂对物体作用力以及由此产生的物体对环境作用力，而且提出的阻抗自适应律能够根据环境对物体的干扰，自适应地调整物体的阻抗参数，从而提高了系统对外部干扰的鲁棒性。从双臂机器人阻抗控制应用角度，利用机器人宇航员实验平台，设计了几种不确定环境的实验场景，包括不确定的空间位置约束以及不确定的人为干扰等，并通过阻抗控制完成了人与机械臂握手、机械臂与固定目标对接、冗余机械臂零空间自避障、双臂夹持搬运物体、人与双臂及其所夹持物体的静态和动态交互等任务，展示了双臂机器人阻抗控制系统在不确定环境中的鲁棒性。

... 通常一般系统中采用软限位的方法进行限位,在系统算法计算得到的关节角大于极限位置的情况下只给定极限位置的控制信号,这种方法带来的后果是末端产生不可预知的轨迹偏差,导致视觉跟踪和控制失败^[4] ...

2015

0.0

... Zhang等^[5]在研究中赋予了人形机器人头部俯仰、偏摆2个自由度,建立了面部的虚拟平面,推导视觉目标和两个关节角关系的二次方程,并采用神经网络算法进行求解 ...

2003

0.0

... Bie等^[6]针对两自由度关节轴正交的机器人头部,建立球面上的目标点和关节转角关系,并直接采用视觉目标空间位置和关节PID闭环控制机制进行视觉伺服控制 ...

2007

0.0

... Hirth等^[7]将机器人头部的动作进行归类,采用人工智能的方法定义机器人的行为习惯 ...

2010

0.0

... Omr cˇen等^[8]的研究对象是一个眼睛能够分别转动的5自由度机器人头部,为了解决两只眼睛观测同一物体时的角度差异,对两只眼睛分别进行了冗余自由度机器人的建模然后连立在一起 ...

2011

0.0

... Giulio^[9]与Omr cˇen的研究对象相同,为了使带有冗余自由度的机器人头部能够稳定地运动,在逆解算法之前引入Kalman滤波对目标位置进行预测 ...

2013

0.0

. 2013, 21(9):2364-2370 DOI:doi:10.3788/OPE.20132109.2364

Person tracking of a mobile robot using improved Mean Shift

采用改进Mean Shift算法的移动机器人行人跟踪

Wang Li-jia , Jia Song-min , Wang Shuang

王丽佳, 贾松敏, 王爽

To improve the performance of person tracking for a mobile robot in complex environments, an adaptive kernel function based Mean Shift algorithm was proposed by using a coarse to fine localization mechanism. In the outer layer, a Radio Frequency Identification Device (RFID) was adopted to detect the person with an ID tag to determine the Region of Interest (ROI) coarsely. In the inner layer, the ROI of a disparity image was processed to estimate an initial searching window. Then, the adaptive kernel based Mean Shift algorithm was applied to location of the person precisely in the left image from a stereo camera. The adaptive kernel function was combined with the regional feature of person and the Epanechnikov function, which can reduce the effect of the background pixel on the target’s color probability distribution. Compared with the traditional Mean Shift algorithm, the presented algorithm can track the target successfully when the background has the same color. Furthermore, the searching area is narrowed by the RFID, so that the computational cost is reduced. The average computing time is 62.11 ms/frame, which satisfies the requirements of real-time target tracking. The experimental results indicate that the proposed tracking method can complete the target tracking in a background with the same color, short-term occlusion, fast moving, and a sudden turn for a mobile robot.

为了提高移动机器人目标跟踪系统在复杂环境中的跟踪性能，提出在双层定位机制下采用基于自适应核函数的Mean Shift算法实现目标跟踪。利用射频识别器件（RFID）检测携带标签的目标，实现外层粗定位并确定感兴趣区域（ROI）；在内层则根据对视差图的ROI的处理结果确定初始搜索窗口，然后应用基于自适应核函数的Mean Shift算法在从立体相机获得的左图中应用基于自适应核函数的Mean Shift算法实现对目标的精确定位。自适应核函数由目标的区域特征与Epanechnikov函数相融合构成，克服了目标边缘处背景像素对目标颜色概率分布的影响。与传统的Mean Shift算法相比，所提方法在同色背景干扰下仍能准确跟踪目标。另外，RFID限定了图像搜索范围，节省了运算开支，图像处理的平均时间为62.11 ms/frame，满足实时跟踪的要求。实验结果表明，该方法可实现移动机器人在同色背景干扰、遮挡、目标快速移动等情况下的目标跟踪。

... 王丽佳^[10]等在目标物体视觉跟踪的研究中,采用改进Mean-shift算法对物体进行粗、精两次定位保证跟踪精度 ...

1986

0.0

... 为避开奇异点,Nakamura^[11]和Wampler^[12]分别建议在运动学逆解求取时采用阻尼最小二乘技术,求取满足式(3)的角度增量最小解 ...

1986

0.0

... 为避开奇异点,Nakamura^[11]和Wampler^[12]分别建议在运动学逆解求取时采用阻尼最小二乘技术,求取满足式(3)的角度增量最小解 ...

2013

0.0

. 2013, 35(5):594-599 DOI:doi:10.3724/SP.J.1218.2013.00594

An constructing method of 3D simulation and virtual motion control system in VC platform

VC平台下机器人虚拟运动控制及3D运动仿真的有效实现方法

Qi Ruo-long , Zhou Wei-jia , Liu Jin-guo

祁若龙, 周维佳, 刘金国

An effective method is presented to implement virtual control and simulation of robot motion in a threedimensional (3D) space in VC (visual C) platform. An open architecture is constructed, which is capable of directly importing and embedding other programs written in C-language, importing robot 3D-solid models generated using SolidWorks, Pro/E, etc. and saving them in a binary-tree-data-structure based simulation model container for the convenient and quick search. Robot kinematic models can be derived based on defined D-H (Denavit-Hartenberg) parameters, and real-time analysis, computation, virtual control and simulation of robot motion can be performed according to a specified path in Windows-based, IntervalZero RTX® supported VC platform. By introducing the Observer Pattern in Computer Design Pattern, a real-time information updating mechanism among various software modules is established in the simulation system to effectively avoid the impact of of Windows' non-real-time data transmission in nature upon the real-time requirements imposed by the simulation system. The friction stir welding (FSW) robot being developed is used as an example to illustrate details about the construction of 3D robot models and their data structures for access, system information communication protocols, and 3D simulation of robot motion based on a given path. A virtual welding process using a simulation-generated robot end-effector trajectory as the tool-end welding path is demonstrated, which shows the effectiveness of the open-architecture, virtual 3D motion control and simulation system.

提出了一种在VC（visual C）平台下实现机器人虚拟运动控制及3维运动仿真的有效方法．该方法建立了一个开放性的体系，能够直接移植或嵌入其它C语言算法程序，能导入SolidWorks、Pro/E等软件生成的机器人3D实体模型，并以二叉树数据结构建立便于快速查找的仿真模型容器进行保存．它还能通过定义机器人D-H（Denavit-Hartenberg）参数建立机器人的运动学模型，并能在基于Windows的IntervalZero RTX®支持的VC平台下，根据指定的路径，实现机器人运动的实时分析、计算、虚拟控制和仿真．这一方法通过引入计算机设计模式中的“观察者”模式，建立仿真系统中各种软件模块之间的实时信息更新机制，有效避免了Windows本身非实时数传机制对仿真系统实时性要求的影响．以正在研制的搅拌摩擦焊接（FSW）机器人为例，详细介绍了机器人3维模型的建立、3维实体的存取数据结构、系统信息的通讯方法、基于给定路径的机器人3维仿真，并演示了用仿真得到的机器人末端实际运动轨迹作为机器人工具末端焊接路径的虚拟焊接及运动控制过程，最终得到了一个开放式的3维虚拟运动控制仿真系统，验证此系统的有效性．

... 基于C++语言的机器人仿真平台构建方法可以参考文献[13] ...