利用Velodyne HDL-32E LIDAR 360° (如图1所示)扫描周围环境, 将采集的三维点云装箱到高度为h=h_max-h_min、半径为R的圆柱体中。设定圆柱体网格单元的角度间隔为Δ θ 、径向间隔为Δ r、高度间隔为Δ b。每个网格单元作为极坐标系中的一个细胞, 构成MRF的各个节点, 见图1。为了找到地面高度所在容器的最优标签值, 并将每个节点网格单元内的LIDAR点分割成地面点和非地面点, 利用网格单元内的点云分布和高度信息来定义标签值, 将网格单元的垂直列均分成B个容器, 标签范围为b={1, 2, …, B}。为避免过多的扫描点增大计算量, 在处理数据之前移除不可能是地面点的扫描点, 即每个网格单元中的悬挂结构, 如树枝等。若扫描点位于3个以上连续的空容器构成的垂直空缺区域上方, 则认定为悬挂点并移除。

图1

Fig.1

	Figure Option ViewDownloadNew Window
	图1 以LIDAR为中心的圆柱形网格地图俯视图Fig.1 Top view of cylindrical grid map centered on LIDAR

MRF用于描述场景中节点的空间交互关系。本文将地面分割问题转化为标准4连接多标签MRF的标记过程。定义无向图G=(V, E), 其中, 节点v_i∈ V, 边(v_i, v_j)∈ E。正常情况下, 标签在各节点间变化缓慢且平滑, 但在物体与地面交界处节点间值变化显著。标签函数f给观测节点v_i分配标签f(v_i)∈ b, 该标记过程的质量取决于多标签MRF中4个相邻节点和观测节点的状态, 通过能量函数E来进行评价:

Ef=Dfvi+Wfvi, fvj(1)

式中:圆周方向上i∈ (1, 2, …, 360° /Δ θ ), 径向方向上i∈ (1, 2, …, R/Δ r); j取i在圆周或径向方向上相邻的序列值; (v_i, v_j)为标准4连接多标签MRF模型的相邻节点对; D(f(v_i))为测量代价函数, 表示分配标签f(v_i)给节点v_i的代价; W(f(v_i), f(v_j))为平滑性代价函数, 表示分配标签f(v_i)和f(v_j)给两个相邻节点的代价。

给定标签f(v_i)指定的地面高度时, 测量代价函数D(f(v_i))用于描述节点处扫描点分布的统计模型。假设测量代价为负对数概率, 则标签的测量代价越小, 该标签是真实地面高度的概率越大。各节点测量代价的大小取决于网格单元内点云分布、LIDAR和该节点间各网格单元的地面高度变化以及是否存在遮挡物。针对4种不同点云分布类型的网格单元, 分别定义相应的测量代价D(f(v_i))。

图2

Fig.2

	Figure Option ViewDownloadNew Window
	图2 网格单元m点云分布的不同类型Fig.2 Different categories of point distribution in grid m

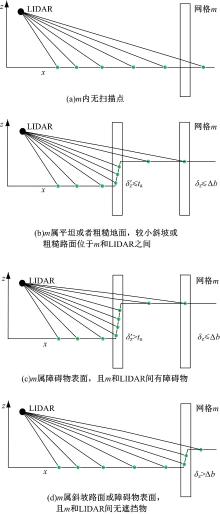
种类1:32线Velodyne LIDAR全方位扫描周围环境, 每秒采集约6万个扫描点, 但仍有部分网格单元无返回值, 见图2(a)。因此, 将空节点的测量代价设为恒定值C, 呈均匀分布, 以保证不同高度的标签容器含有地面点的可能性相同, 见图3(a)。对应的测量代价函数表达式为:

Dfvi=C2

种类2:网格单元m含扫描点。移除悬挂点后, 若m内所有扫描点的纵向高度差最大绝对值δ _z小于容器高度Δ b, 且径向距离小于m的网格单元的扫描点纵向高度差最大绝对值δ '_z小于阈值t_a=3Δ b, 见图2(b), 则表明m和LIDAR间无遮挡, m内扫描点是地面点的概率较大。该约束同时考虑了当前节点和径向近距离节点的点云信息。另外, 阈值t_a包含了可能存在斜坡的情况, 避免了出现文献[7]中车辆顶部错误识别为地面的情况。此时选取含最低点的容器b_s作为m的特征容器, 将m内各容器的测量代价表示为截断阶跃函数, 见图3(b)。

图3

Fig.3

	Figure Option ViewDownloadNew Window
	图3 不同类型点云分布的网格单元对应的测量代价模型Fig.3 Data cost model of grid cell containing different distribution of point cloud

该种类型的网格单元的测量代价函数表达式为:

Dfvi=mingvi-fvi, t(3)

式中:t为截断参数; g(v_i)为节点v_i的特征。

通过计算节点的每个标签f(v_i)与特征容器标签g(v_i)间的差值来保证不同标签容器含地面点概率的差异性, 并利用构建的截断阶跃函数使测量代价模型的鲁棒性增加, 避免出现当点云分布计算出的相邻节点标签差值较大时数值溢出。

种类3:网格单元m含扫描点。移除悬挂点后, 若m内所有扫描点的纵向高度差最大绝对值δ _z存在容忍阈值t_b=Δ b, 但是存在径向距离小于m的网格单元的扫描点纵向高度差最大绝对值δ '_z大于阈值t_a的情况, 见图2(c), 则表明m和LIDAR间存在遮挡, 或m位于侧面倾斜的物体表面, 如车辆顶部。此时选取含最低点的容器b_s为m的特征, 作为边界容器。该边界上方的容器测量代价为半截断阶跃函数, 而边界以下的容器测量代价则为恒定值C, 见图3(c)。该种类型的网格单元的测量代价函数表达式为:

D(f(vi))=min(‖g(vi)-f(vi)‖, t), ifg(vi)> bsC, otherwise（4）

计算节点的每个标签f(v_i)与特征容器g(v_i)上方各标签间的差值, 以保证特征容器上方各标签容器含地面点概率的差异性, 并利用截断过程增加模型的鲁棒性。同时, 采用恒定代价值表示被遮挡的各标签容器包含地面点的可能性相等。此外, 该非对称代价说明当前网格单元的地面高度标签不可能高于b_s。

种类4:网格单元m含扫描点。移除悬挂点后, 若m内所有扫描点的纵向高度差最大绝对值δ _z超过容忍阈值t_b=Δ b, 见图2(d), 此时, 认为m属障碍物, 如墙壁、行人或较小斜坡, 这与径向近距离网格单元是否含扫描点无关。取m内标签最低的非空容器为边界容器, 网格单元的测量代价模型和函数表达式同种类3。

平滑性函数W(f(v_i), f(v_j))用于表示相邻节点间的地面高度变化关系。正常情况下, 相邻节点的高度标签连续近似相同。当高度差增大时, 平滑性代价呈线性增长。为保证较大高度差, 采用式(5)进行截断:

Wfvi, fvj=minsfvi-fvj, d(5)

式中:s为高度差的权重系数; d为节点不连续性的恒定截断值。

在MRF相邻节点间采用LBP算法进行消息传递, 每个节点在每次迭代过程中收集来自其他三个相邻节点的消息, 下一次迭代则更新每个节点到达相邻点的消息, 并归一化计算每个节点处消息的边缘分布。消息传递过程中, 通过最小化能量函数E求解出最优标签f(v_j)。为减少计算复杂度, 选用基于最大积的LBP算法用于最小代价标记过程, 沿多标签MRF的标准4连接图传递消息。算法步骤如下:

(1)用负对数概率初始化所有一维向量消息。

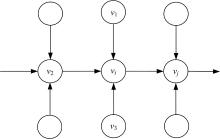
(2)沿径向和圆周方向传播消息, 以顺时针圆周方向为例传递消息, 见图4。选取来自相邻节点容器的最小消息为节点v_j容器标签的新消息。第k次迭代过程中, 更新节点v_i发送给相邻节点v_j的新消息:

mvivjk(f(vj))=minf(vi){W(f(vi), f(vj))+D(f(vi))+∑s∈N(vj)\vjmsvik-1(f(vi))}（6）

式中:k=1, 2, …, K; N(v_i)\v_j为节点v_i的相邻节点, 不包括节点v_j。

图4

Fig.4

	Figure Option ViewDownloadNew Window
	图4 顺时针圆周方向传递消息示例Fig.4 Example for message passing along clockwise direction

(3)k次迭代后, 计算每个节点的信任向量:

bvjfvj=Dvjfvj+∑mvivjkp∈Nvjfvi（7）

采用消息总和计算信任向量时信任值将无限增大, 最终超过浮点数的极限值。因此, 在发送给相邻节点前需归一化处理。有限次的消息传递迭代后, 每个节点处消息收敛, 能量函数可下降到阈值以下。

(4)最小化 bvj(f(v_j)), 选取节点v_j的最优标签f(v_j)用于分离地面点与非地面点:

f(vj)=arg minf(vj)(bvj(f(vj)))（8）

最后, 将每个节点最优标签下方容器的扫描点判定为地面点, 上方的点则为非地面点, 实现每个节点处扫描点的分割。

图6

Fig.6

	Figure Option ViewDownloadNew Window
	图6 简单粗糙路面场景中两种地面分割 算法结果对比Fig.6 Result comparison of two different segmentation algorithms in simple rough road scene

取包含粗糙路面、车辆和墙壁的扇形扫描区域进行分析, 着重研究障碍物区域的地面分割细节, 分别用文献[3]和本文算法进行测试, 结果见图6。由图6(a)可知, 车辆周围的部分地面点错误识别为非地面点, 主要原因在于文献[3]将网格单元内最大高度差值低于给定阈值的扫描点作为地面点, 但是粗糙路面不平整, 部分网格的高度差超出阈值, 但仍为地面点。由图6(b)可知, 本文算法测试结果明显更好。虽然文献[3]和本文算法均利用了高度参数, 但是本文算法将网格内点云分布的高度差约束与邻近网格间的平滑性约束结合, 解决了障碍物与地面接触区域的地面点与非地面点分割问题, 如图6(b)中的车辆附近区域和车身下方区域。

第一种复杂场景是包含行人的不规则岩石区域。分别用文献[6]和本文算法进行测试, 图7(a)中的实验结果表明, 文献[6]方法在LIDAR周围区域分割良好, 但在相对较远区域的地面分割效果较差, 引起分割不足, 主要原因是线性模型对于较大起伏度的地面适应性较差。由图7(b)可知, 本文算法更好地分割了地面点与非地面点。相比文献[6], 本文提出的3种测量代价函数模型很好地解决了不同点云分布类型网格内的地面高度估计问题, 如不连续区域和地面遮挡区域的网格。

图7

Fig.7

	Figure Option ViewDownloadNew Window
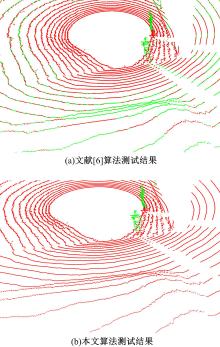	图7 岩石路面场景中两种地面分割算法结果对比Fig.7 Result comparison of two different segmentation algorithms in rocky road scene

第二种复杂场景是包含树木、行人和较大斜坡的非结构化环境。本文算法测试结果如图8所示。由图8(a)可知, 树枝和植被下方的地面点与非地面点正确分割; 将局部区域放大后, 如图8(b)所示, 斜坡上站立的行人A、B和地面点间的接触面也实现了正确分割。此外, 本文算法在实现地面高度估计的基础上成功地识别了斜坡的起伏变化, 有助于对周围环境的整体感知。

图8

Fig.8

	Figure Option ViewDownloadNew Window
	图8 复杂非结构化环境下本文算法测试结果Fig.8 Result of proposed algorithm in complex unstructured scene

为进一步验证算法的可靠性, 手动标记地面真实值, 对所选典型场景的地面分割结果进行定量评估。采用灵敏度(True positive rate, TPR)和特异度(False positive rate, FPR)参数来表示分割结果的好坏, 结果见表1。TPR值越大, 地面点样本被正确分割为地面点的比例越高, 反之则越低。FPR值越大, 非地面点被错误分割为地面点的比例越高, 反之则越低。计算公式如下:

TPR=TPTP+FN(9)

FPR=FPFP+TN(10)

式中:TP为被模型分割为地面点的正样本; FN为被模型分割为非地面点的正样本; FP为被模型分割为地面点的负样本; TN为被模型分割为非地面点的负样本。

表1

Table 1

表1(Table 1)

表1 不同场景下各算法地面分割结果比较 Table 1 Result comparison of road segmentation algorithms in different scenes 场 景 算法 TPR/% FPR/% 简单粗糙路面 文献[3] 94.72 0.23 文献[6] 95.74 0.54 本文 99.91 0.06 岩石路面(含行 人、墙壁等) 文献[3] 76.33 3.21 文献[6] 89.03 2.37 本文 99.56 2.02 复杂非结构化路面 (含多种障碍物) 文献[3] 82.39 3.33 文献[6] 60.57 4.62 本文 92.91 2.12

表1 不同场景下各算法地面分割结果比较 Table 1 Result comparison of road segmentation algorithms in different scenes

由表1可知, 对于简单粗糙道路场景, 文献[3]和[6]中的算法分割性能均较好, 本文算法的测试结果稍优于这两种算法; 对于岩石路面区域和复杂非结构化场景, 本文算法测试结果明显优于这两种算法。文献[3]中的算法将大于给定阈值的不同高度的斜坡误识别为地面, 其单一的高度差约束难以分割复杂场景下的地面点与非地面点。文献[6]中线性模型算法难以选择合适的直线拟合参数, 不易分割远距离岩石区域的地面点, 更适合于室内环境。而本文算法在不同复杂程度的场景中均表现出良好的分割性能, 能克服多种障碍物干扰因素, 其分割准确性和鲁棒性明显优于其他方法。原因在于本文算法基于当前网格单元和径向近距离网格单元的点云分布, 自适应地选择合适的测试代价模型, 提出的测量代价模型有效地解决了部分遮挡的网格单元的地面高度估计问题; 通过利用LBP算法的4方向消息传递过程, 准确分割障碍物和地面间的边界点, 降低了分割不足和过度分割的可能性, 同时也补偿了点云的稀疏分布, 具有更好的鲁棒性。