基于平方根无迹卡尔曼滤波算法的电动汽车质心侧偏角估计

引用本文

田彦涛, 张宇, 王晓玉, 陈华. 基于平方根无迹卡尔曼滤波算法的电动汽车质心侧偏角估计[J].吉林大学学报（工学版）, 2018,48(3): 845-852
TIAN Yan-tao, ZHANG Yu, WANG Xiao-yu, CHEN Hua. Estimation of side-slip angle of electric vehicle based on square-root unscented Kalman filter algorithm[J]. Journal of Jilin University Engineering and Technology Edition, 2018,48(3): 845-852 复制到剪切板

Doi:10.13229/j.cnki.jdxbgxb20170069
Permissions

基于平方根无迹卡尔曼滤波算法的电动汽车质心侧偏角估计

田彦涛^1,², 张宇¹, 王晓玉¹, 陈华¹

1.吉林大学通信工程学院,长春 130022

2.吉林大学工程仿生教育部重点实验室,长春 130022

作者简介:田彦涛(1958-),男,教授,博士生导师.研究方向:复杂系统建模、优化与控制.E-mail:tianyt@jlu.edu.cn

基金:国家重点科技研发计划项目(JFYS2016ZY02001610-02).

摘要

针对电动汽车质心侧偏角不便使用传感器直接测量的问题,提出采用平方根无迹卡尔曼滤波(SR-UKF)算法来估计电动汽车质心侧偏角。基于建立的车辆侧向动力学模型、非线性轮胎动力学模型以及估计得到的质心侧偏角,使用最小二乘法对轮胎侧偏刚度进行估计,得到轮胎侧偏刚度信息。最后,通过试验验证了基于SR-UKF的电动汽车质心侧偏角估计算法具有较高的精度,能够为后续车辆稳定性控制系统的设计提供有效的车辆状态信息。

关键词: 自动控制技术; 侧偏角估计; 轮胎侧偏刚度; 平方根无迹卡尔曼滤波算法; 最小二乘法

中图分类号:TP273 文献标志码:A 文章编号:1671-5497(2018)03-0845-08

Estimation of side-slip angle of electric vehicle based on square-root unscented Kalman filter algorithm

TIAN Yan-tao^1,², ZHANG Yu¹, WANG Xiao-yu¹, CHEN Hua¹

1.College of Communication Engineering,Jilin University,Changchun 130022,China

2.Key Laboratory of Bionic Engineering,Ministry of Education,Jilin University,Changchun 130022,China

Abstract

The side-slip angle of electric vehicle can not be directly and conveniently measured by using sensors. To solve this problem, a Square-Root Unscented Kalman Filter (SR-UKF) algorithm was proposed to estimate the side-slip angle. First, the lateral dynamics model of the vehicle and the nonlinear dynamics model of the tire were established. Then, based on the models and the estimated side-slip angle, the cornering stiffness of the tire was estimated by using least square method. Experiments were carried out to verify the effectiveness of the algorithm in estimating the side-slip angle of electric vehicle. Results show that the proposed method has high precision and can provide effective vehicle state information for the design of the stability control system of the vehicle.

Keyword: automatic control technology; estimation of side-slip angle; cornering stiffness of tire; square-root unscented Kalman filter(SR-UKF) algorithm; least square method

文章图片

0 引言

对于汽车安全系统而言, 在转向行驶时容易产生过度转向、车辆发生侧滑的情况, 严重时危害人身安全, 因此需要对电动汽车侧向稳定性进行研究^[1]。而对车辆侧向运动状态的实时、准确估计是车辆侧向稳定性控制系统研究的基础^[2]。其中, 横摆角速率和车辆侧偏角是两个非常重要的参数, 可以通过调整两者来控制车辆侧向行驶状态。横摆角速率可以由角速度传感器(陀螺仪)直接测量得到; 侧偏刚度能够反映轮胎和路面条件, 对车辆操纵稳定性和安全性有直接影响, 但是轮胎侧偏刚度和车辆侧偏角由于技术和经济原因无法直接测量。因此, 找到一种可以实时获取车辆重要信息的、经济且精确的方法, 成为底盘控制的一个重要问题。

Piyabongkarn等^[3]提出了一种使用廉价传感器实时估计侧偏角的算法, 用于车辆的横摆稳定控制, 该算法结合模型估计和运动学理论, 可以补偿存在的道路倾斜角度和轮胎特性的变化。Doumiati等^[4]提出了一种动态建模和观察的方法来估计侧向力和侧偏角, 为了解决系统的非线性和未建模动态, 设计了扩展和无迹卡尔曼滤波观测器。Nguyen等^[5]提出了一种基于卡尔曼滤波侧偏角估计的电动汽车新电子稳定控制系统, 通过将组合模型误差和外部干扰作为扩展的卡尔曼滤波算法, 实现了侧偏角的准确估计, 同时提高了控制系统的鲁棒性。宗长富等^[6]采用了扩展卡尔曼滤波进行估计, 但是其计算复杂, 在实际控制系统的应用中会受到一定限制。郭洪艳等^[7]提出了基于车辆质心侧偏角估计的非线性全维观测器设计方法。武冬梅等^[8]将二自由度车辆模型简化为以侧向速度为状态的线性估计模型, 用于电动汽车质心侧偏角的估计。刘飞等^[9]利用直接积分法, 对比了基于扩展卡尔曼滤波的质心侧偏角估计算法与基于广义龙贝格观测器的质心侧偏角估计算法的特点。

电动汽车的质心侧偏角对车辆稳定性控制起着重要作用。而现有的车辆质心侧偏角估计算法存在有实时性不强或精度不够等问题, 不能适应各种路面条件。本文提出使用平方根无迹卡尔曼滤波(Square-root unscented Kalman filter, SR-UKF)算法对车辆侧偏角进行实时估计, 并使用递推最小二乘法对轮胎侧偏刚度进行估计, 这种方法考虑了不同道路的实际情况, 具有更好的实时性和鲁棒性。

1 车辆动力学建模

在不考虑车身的俯仰和侧倾运动时, 描述车身在平面内运动的方程有3个:纵向运动方程、侧向运动方程和横摆运动方程^[10]。将车辆视为质量集中在重心的质量块, 质心处为坐标原点。

1.1 车身动力学模型

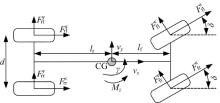
本文车辆侧向动力学模型只考虑车辆的横摆平面, 将车辆的直接横摆力矩作为一个输入变量。直接横摆力矩是由于作用于每个车轮的电磁力矩的不同而产生的。车辆横摆平面的侧向动力学模型如图1所示。

	Figure Option View Download New Window
	图1 车辆横摆平面四轮模型Fig.1 Four-wheel model of vehicle's yaw plane

根据横摆平面四轮模型, 得到车辆侧向动力学模型和基于质心的横摆力矩平衡方程分别为:

$\begin{array}{l} m v_{x} (\overset{\cdot}{β} + γ) = (F_{fl}^{x} + F_{fr}^{x}) \sin δ + (F_{fl}^{y} + \\ F_{fr}^{y}) \cos δ + F_{rl}^{y} + F_{rr}^{y} (1) \\ I_{z} \overset{\cdot}{γ} = (F_{fl}^{x} + F_{fr}^{x}) \sin δ l_{f} + (F_{fl}^{y} + F_{fr}^{y}) \cos δ \cdot \\ l_{f} - (F_{rl}^{y} + F_{rr}^{y}) l_{r} + M_{z} (2) \end{array}$

式中: $m$ 为汽车整车质量, kg; $v_{x}$ 和 $v_{y}$ 分别为车身在大地坐标系下的纵向和侧向行驶速度, m/s; $γ$ 为车身的横摆角速率, rad/s; $β$ 为车辆侧偏角, rad; $δ$ 为车轮转向角, rad; $F_{fl}^{x} 、 F_{fr}^{x}$ 分别为左前轮和右前轮的纵向力; $F_{fl}^{y} 、 F_{fr}^{y}$ 分别为左前轮和右前轮的侧向力; $F_{rl}^{x} 、 F_{rr}^{x}$ 分别为左后轮和右后轮的纵向力; $F_{rl}^{y} 、 F_{rr}^{y}$ 分别为左后轮和右后轮的侧向力, N; $I_{z}$ 为整车在质心处的转动惯量, kg· m²; $l_{f} 、 l_{r}$ 分别为质心到前轴和后轴中心线的距离, m; $d$ 为车轮轮距, m; $M_{z}$ 为直接横摆转矩, 其计算公式如下:

$M_{z} = \frac{d}{2} (F_{rr}^{x} - F_{rl}^{x}) + \frac{d}{2} (F_{fr}^{x} - F_{fl}^{x}) \cos δ (3)$

为了设计的简化, 在对模型精确度影响不大的前提下可以将四轮模型简化为自行车模型, 车辆的侧向和横摆动力学方程可分别简化为:

$\begin{array}{l} m v_{x} (\overset{\cdot}{β} + γ) = F_{f}^{y} \cos δ + F_{r}^{y} (4) \\ I_{z} \overset{\cdot}{γ} = F_{f}^{y} \cos δ l_{f} - F_{r}^{y} l_{r} + M_{z} (5) \end{array}$

当轮胎的侧偏角比较小时, 轮胎的侧向力与轮胎的侧偏角近似成线性关系, 如下所示:

$\{\begin{array}{l} F_{f}^{y} = - 2 C_{f} (β + l_{f} γ / v_{x} - δ) \\ F_{r}^{y} = - 2 C_{r} (β - l_{r} γ / v_{x}) \end{array} (6)$

式中:C_f、C_r分别为前轮和后轮侧向力与轮胎侧偏角线性关系的比例系数。

当转向角非常小时( $\cos δ \approx 1$ ), 根据式(4)~(6)可以近似得到以下状态方程:

$\{\begin{array}{l} \overset{\cdot}{x} (t) = Ax (t) + Bu (t) \\ y (t) = Cx (t) \end{array} (7)$

式中: $x = {[β, γ]}^{T}; u = [δ, M_{z}]^{T}; y = γ;$

$A = [\begin{array}{l} - \frac{2 (C_{f} + C_{r})}{m v_{x}} & - \frac{2 (l_{f} C_{f} - l_{r} C_{r})}{m v_{x}^{2}} - 1 \\ - \frac{2 (l_{f} C_{f} - l_{r} C_{r})}{I_{z}} & - \frac{2 (l_{f}^{2} C_{f} + l_{r}^{2} C_{r})}{I_{z} v_{x}} \end{array}]; B = [\begin{array}{l} \frac{2 C_{f}}{m v_{x}} & 0 \\ \frac{2 l_{f} C_{f}}{I_{z}} & \frac{1}{I_{z}} \end{array}]; C = [\begin{array}{l} 0 & 1 \end{array}] 。$

1.2 轮胎模型

轮胎模型的力学特性和结构参数决定了汽车的主要性能, 因此若要建立精准的整车动力学模型必须首先建立与之相匹配精确的轮胎模型。本文采用由Pacejka等^[11]提出的魔术公式, 在CarSim中有相应的动力学模型, 其一般形式如下:

$\{\begin{array}{l} Y (x') = y (x') + S_{v} \\ y' = θ_{D} \sin {θ_{C} \arctan [θ_{B} x' - θ_{E} (θ_{B} x' - \arctan θ_{B} x')]} \\ x' = X + S_{h} \end{array} (8)$

式中: $Y (x)$ 为输出变量, 一般是纵向力 $F_{x}$ 或侧向力 $F_{y}$ 或回正力矩 $M_{z}$ ; $X$ 为输入变量, 一般是滑移率 $s$ 或侧偏角 $α; θ_{D}$ 为刚度因子; $θ_{C}$ 为形状因子; $θ_{B}$ 为峰值因子; $θ_{E}$ 为曲率因子; $S_{h} 、 S_{v}$ 分别为水平和垂直偏移。

2 侧偏角观测器设计

稳定性系统需要车辆状态信息, 其中, 车辆侧偏角是一个非常重要的参数, 可用于控制系统设计。本文不考虑路面的倾角、车身翻滚运动和悬架的偏转等因素, 设计了平方根无迹卡尔曼滤波算法来估计车辆侧偏角。

2.1 侧向动力学状态方程

电动汽车侧向行驶时, 系统的非线性随机状态方程为:

$\{\begin{array}{l} \overset{\cdot}{x} (t) = f (x (t), u (t)) + ω (t) \\ y (t) = h (x (t)) + υ (t) \end{array} (9)$

式中: $ω (t)$ 为过程噪声; $υ (t)$ 为测量噪声。

定义车辆侧偏角 $β 、$ 横摆角速率 $γ$ 和前、后轮侧向力 $F_{f}^{y} 、 F_{r}^{y}$ 组成状态向量 $x$ 为:

$x = {[\begin{array}{l} β & γ & F_{f}^{y} & F_{r}^{y} \end{array}]}^{T} = {[\begin{array}{l} x_{1} & x_{2} & x_{3} & x_{4} \end{array}]}^{T} (10)$

横摆角速率和前、后轮侧向力组成观测向量 $y,$ 如下所示:

$\begin{array}{l} y = {[\begin{array}{l} γ & F_{f}^{y} & F_{r}^{y} \end{array}]}^{T} = {[\begin{array}{l} y_{1} & y_{2} & y_{3} \end{array}]}^{T} \\ (11) \end{array}$

输入向量 $u$ 由转向角、前后轮的驱动力组成:

$\begin{array}{l} u = {[\begin{array}{l} δ & F_{fl}^{x} & F_{fr}^{x} & F_{rl}^{x} & F_{rr}^{x} \end{array}]}^{T} = \\ [{\begin{array}{l} u_{1} & u_{2} & u_{3} & u_{4} & u \end{array}}_{5}]^{T} (12) \end{array}$

将状态方程(9)中的过程噪声和测量噪声假设为不相关的白色噪声, 那么系统的非线性状态方程 $f (x (t), u (t))$ 和观测方程 $h (x (t))$ 分别为:

$\begin{array}{l} f (x (t), u (t)) = \\ \{\begin{array}{l} f_{1} (x, u) = - x_{2} + \frac{\cos u_{1}}{m v_{x}} x_{3} + \frac{x_{4}}{m v_{x}} \\ f_{2} (x, u) = l_{f} \cos u_{1} x_{3} {I_{z}}^{- 1} - l_{r} x_{4} {I_{z}}^{- 1} + \\ d (u_{5} - u_{4} + u_{3} \cos u_{1} - u_{2} \cos u_{1}) (2 I_{z})^{- 1} \\ f_{3} (x, u) = 0 \\ f_{4} (x, u) = 0 \end{array} (13) \\ h (x (t)) = \{\begin{array}{l} h_{1} (x) = x_{2} \\ h_{2} (x) = x_{3} \\ h_{3} (x) = x_{4} \end{array} (14) \end{array}$

2.2 平方根无迹卡尔曼滤波算法设计

在非线性的简化车辆动力学模型基础上, 本文使用无迹卡尔曼滤波器(UKF)进行状态估计。但在实际应用中, UKF算法由于噪声和计算误差会出现协方差矩阵非正定的问题, 本文应用平方根无迹卡尔曼滤波(SR-UKF)来提高数值的稳定性, 保证状态协方差矩阵半正定性, 进而估计车辆侧偏角^{[12, 13]}。

为了能在计算机上实现, 本文采用欧拉近似理论将其离散化为如下形式:

$\{\begin{array}{l} x_{k} = f (x_{k - 1}, u_{k}) + ω_{k} \\ y_{k} = h (x_{k}) + υ_{k} \end{array} (15)$

式中:状态变量 $x_{k} \in R^{n};$ 输入变量 $u_{k} \in R^{r}; k$ 时刻的输出变量 $y_{k} \in R^{m} 。$

SR-UKF算法步骤如下所示。

(1)初始化。在UKF的基础上, 通过乔里斯基(Cholesky)分解后的矩阵平方根计算状态协方差:

$\{\begin{array}{l} {\hat{x}}_{0} = E [x_{0}] \\ S_{x, 0}^{-} = chol \{E [(x_{0} - {\hat{x}}_{0}) {(x_{0} - {\hat{x}}_{0})}^{T}]\} \end{array} (16)$

式中:协方差平方根有“ -” 标志的是下三角矩阵, 没有的是上三角矩阵; chol(· )为乔里斯基分解。

(2)Sigma点的选择计算和时间更新。主要包括如下两步:

Step1 非线性状态方程的预测和状态协方差矩阵平方根的计算:

$\{\begin{array}{l} χ_{k - 1} = [{\hat{x}}_{k - 1}, {\hat{x}}_{k - 1} \pm \sqrt{(n + λ) S_{k - 1}}] \\ χ_{k |k - 1}^{*} = f (χ_{k - 1}, u_{k - 1}) \\ {\hat{x}}_{k}^{-} = \overset{2 n}{\sum_{i = 0}} {ω^{m}}_{i} χ_{i, k |k - 1}^{*} \\ S_{k} = qr \{[\sqrt{{ω^{c}}_{1}} (χ_{1 : 2 n, k |k - 1}^{*} - {\hat{x}}_{k}^{-}) \sqrt{Q}]\} \\ S_{k}^{-} = cholupdate \{S_{k}^{-}, χ_{0, k}^{*} - {\hat{x}}_{k}^{-}, {ω^{c}}_{0}\} \end{array} (17)$

式中:cholupdate(· )为乔里斯基分解的更新函数; qr(· )为QR分解函数; $Q$ 为过程噪声协方差矩阵。

Step2 Sigma点的更新传播和非线性观测方程的进一步预测:

$\{\begin{array}{l} χ_{k - 1} = [{\hat{x}}_{k}^{-}, {\hat{x}}_{k}^{-} \pm \sqrt{(n + λ) S_{k}^{-}}] \\ γ_{k |k - 1} = h (χ_{k - 1}) \\ {\hat{y}}_{k}^{-} = \overset{2 n}{\sum_{i = 0}} {ω^{m}}_{i} γ_{i, k |k - 1} \end{array} (18)$

式中:相关权重因子如下:

$\{\begin{array}{l} {ω^{m}}_{0} = \frac{λ}{n + λ} \\ {ω^{c}}_{0} = \frac{λ}{n + λ} + (1 - α_{0}^{2} + β_{0}) \\ {ω^{m}}_{i} = {ω^{c}}_{i} = \frac{1}{2 (n + λ)}, i = 1, 2, \dots, 2 n \\ λ = α_{0}^{2} (n + ε) - n, ε \geq 0 \end{array} (19)$

式中: ${ω^{m}}_{i}$ 为均值的权; ${ω^{c}}_{i}$ 为方差的权; $λ$ 为调节参数, 为了保证方差矩阵的半正定性, 取 $ε = 0; α_{0}$ 表示Sigma点偏离期望值 $\bar{x}$ 的程度, 通常为 $1 \times 10^{- 4} < α < 1; β_{0}$ 表示 $x$ 的分布情况, 对于高斯分布, $β_{0} = 2$ 为最优, $n$ 为状态变量的维数。

(3)量测更新。主要包括观测量协方差矩阵、 ${\hat{x}}_{k}^{-}$ 与 ${\hat{y}}_{k}^{-}$ 间互协方差 $P_{xy}$ 和滤波增益 $K_{k}$ 的计算以及状态和状态协方差平方根的更新:

$\begin{array}{l} \{\begin{array}{l} S_{y, k} = qr \{[\sqrt{{ω^{c}}_{1 : 2 n}} (γ_{1 : 2 n, k |k - 1} - {\hat{y}}_{k}^{-}) \sqrt{R}]\} \\ S_{y, k}^{-} = cholupdate \{S_{y, k}, γ_{0, k |k - 1} - {\hat{y}}_{k}^{-}, {ω^{c}}_{0}\} \end{array} (20) \\ \{\begin{array}{l} P_{xy} = \overset{2 n}{\sum_{i = 0}} {ω^{c}}_{i} (χ_{i, k |k - 1}^{*} - {\hat{x}}_{k}^{-}) {(γ_{i, k |k - 1} - {\hat{y}}_{k}^{-})}^{T} \\ K_{k} = (P_{xy} / S_{y, k}^{- T}) / S_{y, k}^{-} \end{array} (21) \\ \{\begin{array}{l} {\hat{x}}_{k} = {\hat{x}}_{k}^{-} + K_{k} (y_{k} - {\hat{y}}_{k}^{-}) \\ U = K_{k} S_{y, k}^{-} \\ S_{x, k}^{-} = cholupdate \{S_{x, k / k - 1}, U, - 1\} \end{array} (22) \end{array}$

式中: $R$ 为测量噪声协方差矩阵。

本文选择 $Q 和 R$ 为对角矩阵形式, 协方差的过程和测量噪声矩阵如下:

$\{\begin{array}{l} Q_{ρ} = diag [Q_{β}, Q_{γ}, Q_{F_{f}^{y}}, Q_{F_{r}^{y}}] \\ R_{σ} = diag [R_{γ}, R_{F_{f}^{y}}, R_{F_{r}^{y}}] \end{array} (23)$

本文中应用的简化车辆动力学模型是精确可靠的, 所以过程噪声设置得相对较小。

3 轮胎侧偏刚度估计

侧偏刚度是一个随轮胎侧偏角和路面摩擦变化而变化的重要参数, 可以利用在线估计的侧偏刚度来改善主动转向系统性能。本文利用上述侧偏角信息, 采用最小二乘法^[14]估计轮胎侧偏刚度。

3.1 轮胎侧向力模型

轮胎侧向力在车辆动力学中起着重要作用。当轮胎侧偏角出现时, 在接触路径侧向力将施加于轮胎上^[15]。当轮胎侧滑角很小时, 侧向力与轮胎侧偏角和侧偏刚度成正比:

$F^{y} = C_{0} β (24)$

式中: $F^{y}$ 为轮胎侧向力; $C_{0}$ 为轮胎侧偏刚度。

假设左、右侧轮胎侧偏刚度相同, 则左侧和右侧的侧向力结合可以近似表示为:

$\{\begin{array}{l} F_{f}^{y} = F_{fl}^{y} + F_{fr}^{y} = - 2 C_{f} (β + l_{f} γ / v_{x} - δ) \\ F_{r}^{y} = F_{rl}^{y} + F_{rr}^{y} = - 2 C_{r} (β - l_{r} γ / v_{x}) \end{array} (25)$

3.2 轮胎侧偏刚度估计

定义两个虚拟参数为:

$X_{1} = C_{f}, X_{2} = C_{r} (26)$

建立如下的一个线性回归方程:

$y (t) = φ^{T} (t) X (t) (27)$

式中: $y (t) 、 φ^{T} (t)$ 分别为测量输出和输入数据向量; $X (t)$ 为待估计的参数向量, 其表达式分别为:

$\{\begin{array}{l} y (t) = {[\begin{array}{l} y_{1} & y_{2} \end{array}]}^{T} \\ φ^{T} (t) = [\begin{array}{l} φ_{11} & φ_{12} \\ φ_{21} & φ_{22} \end{array}] \\ X (t) = {[\begin{array}{l} X_{1} & X_{2} \end{array}]}^{T} \end{array} (28)$

式中: $y_{1} = F_{f}^{y}; y_{2} = F_{r}^{y}; φ_{11} = - 2 (β + \frac{γ l_{f}}{v_{x}} - δ); φ_{12} = φ_{22} = 0; φ_{21} = - 2 (β - \frac{γ l_{r}}{v_{x}}) 。$

本文采用带遗忘因子的递推最小二乘法估计轮胎的侧偏刚度, 算法过程如下:

$\begin{array}{l} \begin{array}{l} \hat{X} (t) = \hat{X} (t - 1) + ϕ {K (t) [y (t) - φ^{T} (t) \cdot \\ \hat{X} (t - 1)]} \\ K (t) = \frac{P (t - 1) X (t)}{λI + φ^{T} (t) P (t) X (t)} (29) \\ P (t) = \frac{1}{λ} [I - K (t) φ^{T} (t)] P (t - 1) \end{array} \\ ϕ = \{\begin{array}{l} 0, if {\hat{X}}_{j} \geq X_{j, \max} and F > 0 \\ 0, if {\hat{X}}_{j} \leq X_{j, \min} and F < 0 \\ F, 其他 \end{array} (30) \end{array}$

式中: $F = K (t) [y (t) - φ^{T} (t) \hat{X} (t - 1)]; I$ 为单位矩阵; $K (t)$ 为估计的增益矩阵; $P (t)$ 为协方差矩阵; 遗忘因子 $λ$ 选定为一个比1稍小一点的正的常数。

实际中, 轮胎侧偏刚度在确定的路面条件下, 是在一定范围内的。本文限定 $C_{f} \in (C_{f, \min}, C_{f, \max}), C_{r} \in (C_{r, \min}, C_{r, \max}) 。$ 在转向角近似为零时, 所得的试验数据也近似为零, 此时估计值将变得不确定。所以在转向角很小时, 设置递归最小二乘法的数据不更新。

4 仿真试验结果及分析

为了验证本文所提出估计算法的有效性, 选择专业的汽车仿真软件CarSim和Simulink进行联合仿真试验。将CarSim车辆模型中输出的变量作为实际参考值, 与采用SR-UKF估计算法得到的车辆侧偏角估计值和遗忘因子最小二乘法估计得到的轮胎侧偏刚度估计值进行比较。但由于CarSim车辆模型中输出的变量不包含轮胎侧偏刚度数据变量, 所以本文利用已知的轮胎侧向力和车辆侧偏角信息将其计算出来, 作为实际参考值进行对比。

本文设定CarSim车辆模型中汽车参数如表1所示。

表1 电动汽车参数 Table 1 Parameters of electric vehicle

在CarSim的测试规范模块设置车辆参数和仿真条件。车辆以80 km/h的初速度行驶, 方向盘输入转向角设置为正弦信号输入, 其周期为4 s、振幅为60° 。本文假设汽车分别在路面附着系数为0.9和0.4的路面上行驶, 进行仿真试验, 得到在不同路面条件下车辆状态信息、车辆侧偏角和轮胎侧偏刚度的估计结果图。

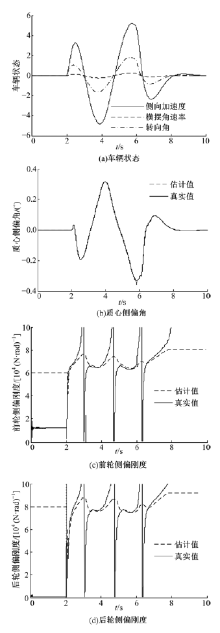图2为 $μ = 0.9$ 时的车辆侧向运动相关状态估计结果。从图2中可以看到:转向角正弦输入在2~6 s期间起作用, 图2(a)为在路面附着系数为0.9时的侧向加速度、横摆角速率和输出转向角随输入的正弦信号的变化趋势和状态。从图2(b)中可以看出:在正弦信号输入状态下, 本文所设计的平方根无迹卡尔曼观测器(SR-UKF)可以准确、有效地估计出车辆侧偏角的变化, 估计误差很小, 它的准确估计为下文的控制设计和分析提供了有效的车辆状态信息。

	Figure Option View Download New Window
	图2 μ =0.9时的车辆侧偏角与轮胎侧偏刚度估计结果Fig.2 Eestimation results of side slip angle and cornering stiffness of tire when μ =0.9

图2(c)(d)分别为车辆的前、后轮侧偏刚度的估计值与真实值对比图, 可以看出:本文采用的遗忘因子递推最小二乘法有很好的实时性, 前、后轮侧偏刚度的估计值能够较好地跟随真实值的变化; 前、后轮的侧偏刚度真实值在转向角为零或在零附近时, 产生剧烈的震荡, 因为真实值是通过输出的已知量计算得到的, 可能是在该时刻轮胎侧偏角非常小(近似为零), 导致轮胎侧偏刚度突变增大。这种突变对控制系统有一定的影响, 所以在转向角很小或在零附近时, 递归算法不进行数据的更新, 从而消除转向角很小时, 前、后轮侧偏刚度产生的剧烈震荡。

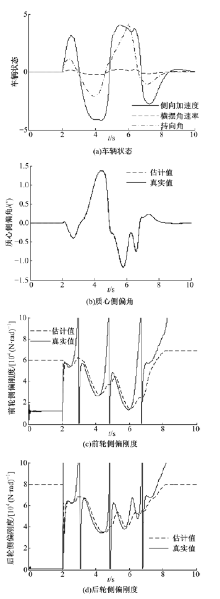图3为 $μ = 0.4$ 时的车辆侧向运动相关状态估计结果。图3(a)为路面附着系数为0.4时的侧向加速度、横摆角速率和输出转向角的随着输入的正弦信号的变化趋势和状态。从图3(b)中可以看出:此时的质心侧偏角的估计值也能很好地跟随真实值的变化, 具有较好的实时性, 相对于路面条件良好时, 侧偏角的值相对增大了一些, 但是估计的准确度依然很好, 误差较小; 图3(c)(d)分别为车辆前、后轮侧偏刚度的估计值与真实值的对比效果图, 可以看出:图中前、后轮侧偏刚度的估计值也能够实时跟随真实值变化。

	Figure Option View Download New Window
	图3 μ =0.4时的车辆侧偏角与轮胎侧偏刚度估计结果Fig.3 Eestimation results of side slip angle and correring stiffness of tire when μ =0.4

图4为不同路面条件下的侧偏角估计误差。从图4可以看出:在不同路面条件下, 本文所设计的状态观测器都能很好地估计车辆侧偏角, 估计误差都很小, 能为稳定性控制提供可靠的车辆状态信息。

	Figure Option View Download New Window
	图4 侧偏角估计误差Fig.4 Estimation error of side slip angle

5 结束语

本文提出采用平方根无迹卡尔曼滤波(SR-UKF)观测器对车辆侧偏角进行实时估计。利用估计到的侧偏角, 使用带遗忘因子的递推最小二乘法对轮胎侧偏刚度进行估计。最后, 通过Simulink仿真试验和CarSim联合仿真试验验证了本文估计方法的有效性。结果表明:在不同路面条件下, 本文方法获得的估计值能够实时地跟随实际值的变化, 能够达到控制系统设计的要求。本文研究对于后期电动车侧向稳定性控制的深入研究具有重要意义。

The authors have declared that no competing interests exist.

参考文献

文献列表

[1]	赵伟. 汽车动力学稳定性横摆力矩和主动转向联合控制策略的仿真研究[D]. 西安: 长安大学汽车学院, 2008. Zhao Wei. Simulation research on combined control strategy of yaw moment and active steering for vehicle dynamic stability[D]. Xi'an: School of Automobile, Chang'an University, 2008. [本文引用:1]
[2]	Fu C, Hoseinnezhad R, Hadiashar A B, et al. Electric vehicle side-slip control via electronic differential[J]. International Journal of Vehicle Autonomous Systems, 2015, 13(1): 1-26. [本文引用:1]
[3]	Piyabongkarn D, Rajamani R, Grogg J, et al. Development and experimental evaluation of a slip angle estimator for vehicle stability control[J]. IEEE Transactions on Control Systems Technology, 2009, 17(1): 78-88. [本文引用:1]
[4]	Doumiati M, Victorino A C, Charara A, et al. Onboard realtime estimation of vehicle lateral tire-road forces and sideslip angle[J]. IEEE/ASME Transactions on Mechatronics, 2011, 16(4): 601-614. [本文引用:1]
[5]	Nguyen B M, Wang Y F, Fujimoto H, et al. Electric vehicle stability control based on disturbance accommodating Kalman filter using GPS[C]∥IEEE International Conference on Mechatronics, Takamatsu, Japan, 2013: 382-387. [本文引用:1]
[6]	宗长富, 胡丹, 杨肖, 等. 基于扩展Kalman滤波的汽车行驶状态估计[J]. 吉林大学学报: 工学版, 2009, 39(1): 9-13. Zong Chang-fu, Hu Dan, Yang Xiao, et al. Vehicle driving state estimation based on extended Kalman filter[J]. Journal of Jilin University (Engineering and Technology Edition), 2009, 39(1): 9-13. [本文引用:1]
[7]	郭洪艳, 陈虹, 丁海涛, 等. 基于Uni-Tire轮胎模型的车辆质心侧偏角估计[J]. 控制理论与应用, 2010, 27(9): 1131-1139. Guo Hong-yan, Chen Hong, Ding Hai-tao, et al. Vehicle side-slip angle estimation based on Uni-Tire model[J]. Control Theory&Applications, 2010, 27(9): 1131-1139. [本文引用:1]
[8]	武冬梅, 丁海涛, 郭孔辉, 等. 基于线性估计模型的电动汽车质心侧偏角估计[J]. 吉林大学学报: 工学版, 2014, 44(4): 901-906. Wu Dong-mei, Ding Hai-tao, Guo Kong-hui, et al. Sideslip angle estimation based on linear estimation model for electric vehicle[J]. Journal of Jilin University (Engineering and Technology Edition), 2014, 44(4): 901-906. [本文引用:1]
[9]	刘飞, 熊璐, 邬肖鹏, 等. 车辆质心侧偏角估计算法设计与对比分析[J]. 同济大学学报: 自然科学版, 2015, 43(3): 448-455. Liu Fei, Xiong Lu, Wu Xiao-peng, et al. Vehicle sideslip angle estimation and contrastive analysis[J]. Journal of Tongji University(Natural Science), 2015, 43(3): 448-455. [本文引用:1]
[10]	Nam K, Fujimoto H, Hori Y. Lateral stability control of in-wheel-motor-driven electric vehicles based on sideslip angle estimation using lateral tire force sensors[J]. IEEE Transactions on Vehicular Technology, 2012, 61(5): 1972-1985. [本文引用:1]
[11]	Pacejka H B, Bakker E. The magic formula tyre model[J]. Vehicle System Dynamics, 1992, 21(Sup. 1): 1-18. [本文引用:1]
[12]	Jafarzadeh S, Lascu C, Fadali M S. Square root unscented Kalman filters for state estimation of induction motor drives[J]. IEEE Transactions on Industry Applications, 2013, 49(1): 92-99. [本文引用:1]
[13]	贾瑞才. 重力/地磁辅助的欧拉角无迹卡尔曼滤波姿态估计[J]. 光学精密工程, 2014, 22(12): 3280-3286. Jia Rui-cai. Attitude estimation base on gravity/magnetic assisted Euler angle UKF[J]. Optics and Precision Engineering, 2014, 22(12): 3280-3286. [本文引用:1]
[14]	李海涛, 房建成. 自适应角速度估计器在磁悬浮控制力矩陀螺框架伺服系统中的应用[J]. 光学精密工程, 2008, 16(1): 97-102. Li Hai-tao, Fang Jian-cheng. Application of adaptive angle-rate estimator to gimbal of MGCMG[J]. Optics and Precision Engineering, 2008, 16(1): 97-102. [本文引用:1]
[15]	Tielking J T. A comparative evaluation of five tire traction models[J/OL]. [2017-01-10]. https:∥deepblue.lib.umich.edu/bitstream/handle/2027.42/330/28983.0001.001.pdf?sequence=2. [本文引用:1]

2008

0.0

. 2008, :- DOI:doi:10.7666/d.y1529068

Simulation research on combined control strategy of yaw moment and active steering for vehicle dynamic stability

汽车动力学稳定性横摆力矩和主动转向联合控制策略的仿真研究

Zhao Wei

赵伟

现代汽车的发展趋势是“安全、节能、环保”，汽车主动安全性问题是影响道路交通安全状况的一个重要方面，而汽车稳定性控制系统是提高汽车主动安全性的有效措施，也是当前国内外的研究热点。本文针对汽车在转弯工况下的行驶和制动稳定性，利用横摆力矩和主动转向控制技术进行汽车稳定性控制，结合模糊控制和Fuzzy-PID控制理论，确定相关的控制策略和控制算法，对两种控制模式单独控制和联合控制机理进行了研究，为提高汽车稳定性集成控制提供了一定的研究思路。论文从车辆动力学的本质出发，在已有的轮胎实验数据基础上，利用神经网络方法得到轮胎力模型...

... 0 引言对于汽车安全系统而言,在转向行驶时容易产生过度转向、车辆发生侧滑的情况,严重时危害人身安全,因此需要对电动汽车侧向稳定性进行研究^[1] ...

2015

0.0

... 而对车辆侧向运动状态的实时、准确估计是车辆侧向稳定性控制系统研究的基础^[2] ...

2009

0.0

... Piyabongkarn等^[3]提出了一种使用廉价传感器实时估计侧偏角的算法,用于车辆的横摆稳定控制,该算法结合模型估计和运动学理论,可以补偿存在的道路倾斜角度和轮胎特性的变化 ...

2011

0.0

... Doumiati等^[4]提出了一种动态建模和观察的方法来估计侧向力和侧偏角,为了解决系统的非线性和未建模动态,设计了扩展和无迹卡尔曼滤波观测器 ...

2013

0.0

... Nguyen等^[5]提出了一种基于卡尔曼滤波侧偏角估计的电动汽车新电子稳定控制系统,通过将组合模型误差和外部干扰作为扩展的卡尔曼滤波算法,实现了侧偏角的准确估计,同时提高了控制系统的鲁棒性 ...

2009

0.0

. 2009, 39(1):9-13

Vehicle driving state estimation based on extended Kalman filter

基于扩展Kalman滤波的汽车行驶状态估计

Zong Chang-fu , Hu Dan , Yang Xiao

宗长富, 胡丹, 杨肖

... 宗长富等^[6]采用了扩展卡尔曼滤波进行估计,但是其计算复杂,在实际控制系统的应用中会受到一定限制 ...

2010

0.0

. 2010, 27(9):1131-1139

Vehicle side-slip angle estimation based on Uni-Tire model

基于Uni-Tire轮胎模型的车辆质心侧偏角估计

Guo Hong-yan , Chen Hong , Ding Hai-tao

郭洪艳, 陈虹, 丁海涛

... 郭洪艳等^[7]提出了基于车辆质心侧偏角估计的非线性全维观测器设计方法 ...

2014

0.0

. 2014, 44(4):901-906 DOI:doi:10.13229/j.cnki.jdxbgxb201404001

Sideslip angle estimation based on linear estimation model for electric vehicle

基于线性估计模型的电动汽车质心侧偏角估计

Wu Dong-mei , Ding Hai-tao , Guo Kong-hui

武冬梅, 丁海涛, 郭孔辉

Sideslip angle estimation is the key technique of vehicle stability control system. For electric vehicle, the information of driving torque and braking torque on wheels can be fully utilized to calculate the longitudinal force on the tire. If the longitudinal slip of the tire is large enough, the lateral force on the tire can be expressed with the longitudinal force on the tire and the tire slip angle. If the longitudinal slip of the tire is small, the nonlinear tire model is locally linearized. In such way, the two degrees of freedom vehicle model can be simplified to a linear model, whose state variable is the vehicle lateral speed and can be used to estimate the sideslip angle of the vehicle. Simulation results show that the estimation accuracy of the sideslip angle with the linear estimation model is high enough, and its dependence on the road surface friction coefficient is small. In addition, the calculation is simple due to the linearity of the model. The estimation method can be applied to the vehicle stability control system.

质心侧偏角估计是车辆稳定性控制系统中的关键技术和难点, 针对电动汽车, 本文充分利用车轮上的驱动力矩和制动力矩信息, 计算出了轮胎上的纵向力。并将轮胎侧向力用纵向力和侧偏角表示或进行局部线性化。这样可以将二自由度车辆模型简化为以侧向速度为状态的线性估计模型, 用于电动汽车质心侧偏角的估计。仿真结果表明:基于线性估计模型的质心侧偏角估计器的估计精度较高, 对路面摩擦因数的依赖程度小, 并且计算简单, 可以应用于车辆的稳定性控制系统中。

... 武冬梅等^[8]将二自由度车辆模型简化为以侧向速度为状态的线性估计模型,用于电动汽车质心侧偏角的估计 ...

2015

0.0

. 2015, 43(3):448-455 DOI:doi:10.11908/j.issn.0253-374x.2015.03.020

Vehicle sideslip angle estimation and contrastive analysis

车辆质心侧偏角估计算法设计与对比分析

Liu Fei , Xiong Lu , Wu Xiao-peng

刘飞, 熊璐, 邬肖鹏

It is difficult to estimate the vehicle sideslip angle which is a very important indicator of automotive lateral movement. In order to estimate the sideslip angle accurately, the kinematics direct integral method, the estimation methods based on extended Kalman filter and the extended Luenberger observer were developed in this paper. Then, the three developed sideslip angle estimation methods were adjusted and validated in several typical testing conditions in simulation, with a certain intensity of noise. The characteristics and the adaptability of different methods were also analyzed. The kinematics direct integral method cannot estimate accurately in long time range, but can swiftly show the tendency of the change of sideslip angle in extreme conditions; The extended Kalman filter can generally estimate very well, but it usually overestimates in some dynamic conditions; The extended Luenberger observer can also estimate well, but it often underestimates in some conditions.

车辆质心侧偏角是描述车辆侧向运动状态的重要变量之一，同时也很难准确估计.为此设计了基于运动学的直接积分法，基于扩展卡尔曼滤波的质心侧偏角估计算法和基于广义龙贝格观测器的质心侧偏角估计算法.对信号引入一定强度的噪声，通过多种典型工况对质心侧偏角估计算法进行调试与验证，分析不同算法的特点和工况适应性.直接积分法在长时间尺度下无可用性，但在极限工况下能较为快速地描述质心侧偏角变化趋势；卡尔曼滤波算法整体估计效果较好，但在一些动态工况存在估计偏差，且多为高估；龙贝格观测器算法在大部分工况都能获得良好效果，但在某些情况下存在估计偏差，且多为低估.

... 刘飞等^[9]利用直接积分法,对比了基于扩展卡尔曼滤波的质心侧偏角估计算法与基于广义龙贝格观测器的质心侧偏角估计算法的特点 ...

2012

0.0

... 1 车辆动力学建模在不考虑车身的俯仰和侧倾运动时,描述车身在平面内运动的方程有3个:纵向运动方程、侧向运动方程和横摆运动方程^[10] ...

1992

0.0

... 本文采用由Pacejka等^[11]提出的魔术公式,在CarSim中有相应的动力学模型,其一般形式如下: ...

2013

0.0

... 但在实际应用中,UKF算法由于噪声和计算误差会出现协方差矩阵非正定的问题,本文应用平方根无迹卡尔曼滤波(SR-UKF)来提高数值的稳定性,保证状态协方差矩阵半正定性,进而估计车辆侧偏角^[12,13] ...

2014

0.0

. 2014, 22(12):3280-3286 DOI:doi:10.3788/OPE.20142212.3280

Attitude estimation base on gravity/magnetic assisted Euler angle UKF

重力/地磁辅助的欧拉角无迹卡尔曼滤波姿态估计

Jia Rui-cai

贾瑞才

摘　要：为了克服应用扩展卡尔曼滤波（EKF）的姿态估计算法的线性化误差问题,提出了一种基于重力/地磁辅助的欧拉角无迹卡尔曼滤波（UKF）姿态估计算法来提升低成本微机电系统（MEMS）的姿态测量精度。应用重力与地磁数据抑制了MEMS姿态误差快速发散问题;将欧拉角作为状态,应用四元数完成时间更新过程中的姿态更新,避免了四元数作为状态的规范化问题及欧拉角姿态更新精度低的问题;由于UKF滤波器不存在线性化误差,故其具有更好的稳定性和姿态估计精度。应用实际MEMS数据开展的算法验证实验显示：与EKF姿态估计算法相比,提出的UKF姿态估计算法得到的俯仰与横滚角精度提高了近20%,航向角精度提高了12.1%。结果表明：本文提出算法的精度更高;然而由于UKF算法对状态协方差估计不足,其收敛时间有所增加。

2008

0.0

. 2008, 16(1):97-102

Application of adaptive angle-rate estimator to gimbal of MGCMG

自适应角速度估计器在磁悬浮控制力矩陀螺框架伺服系统中的应用

Li Hai-tao , Fang Jian-cheng

李海涛, 房建成

... 本文利用上述侧偏角信息,采用最小二乘法^[14]估计轮胎侧偏刚度 ...

0.0

... 当轮胎侧偏角出现时,在接触路径侧向力将施加于轮胎上^[15] ...