Journal of Jilin University(Engineering and Technology Edition) ›› 2025, Vol. 55 ›› Issue (7): 2434-2443.doi: 10.13229/j.cnki.jdxbgxb.20231089

Previous Articles    

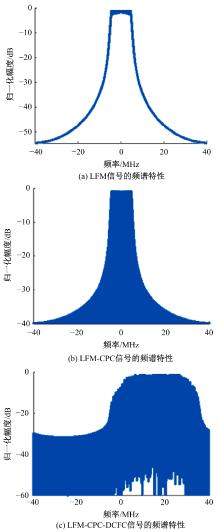
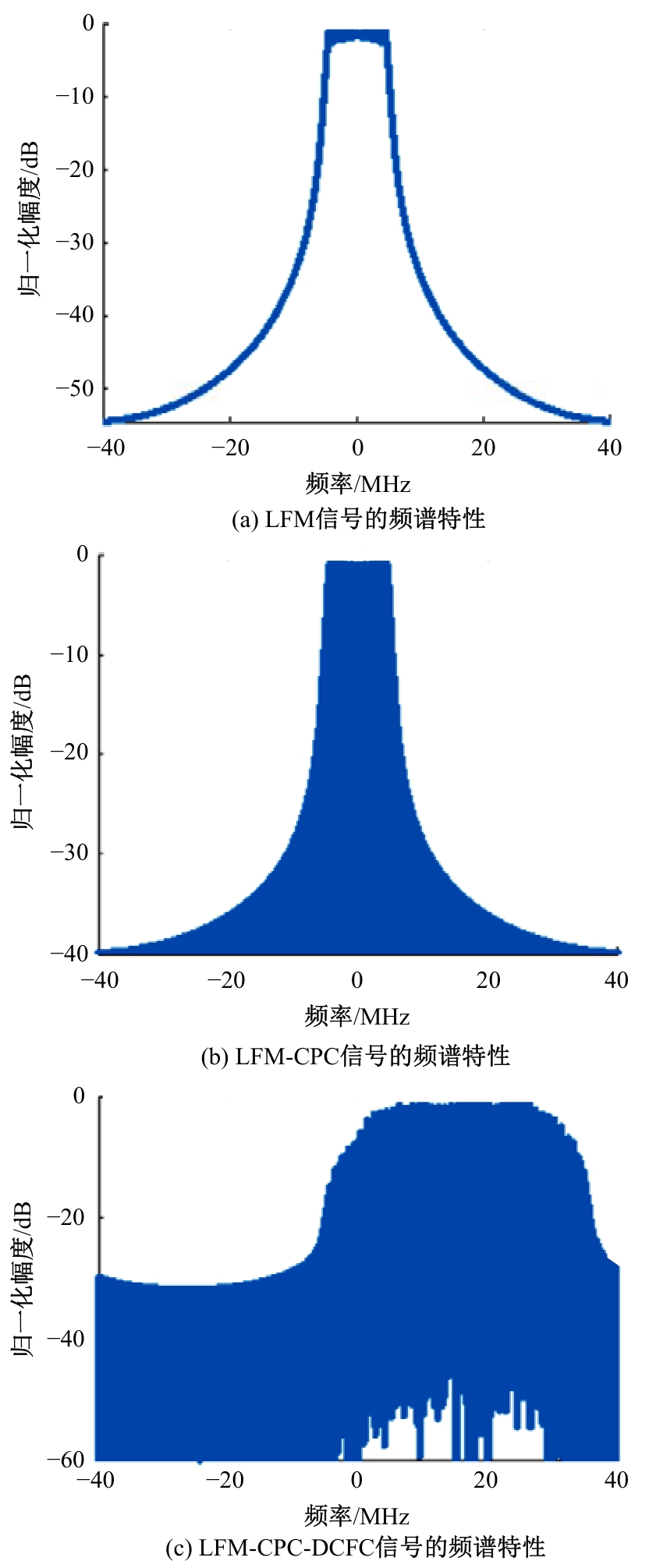
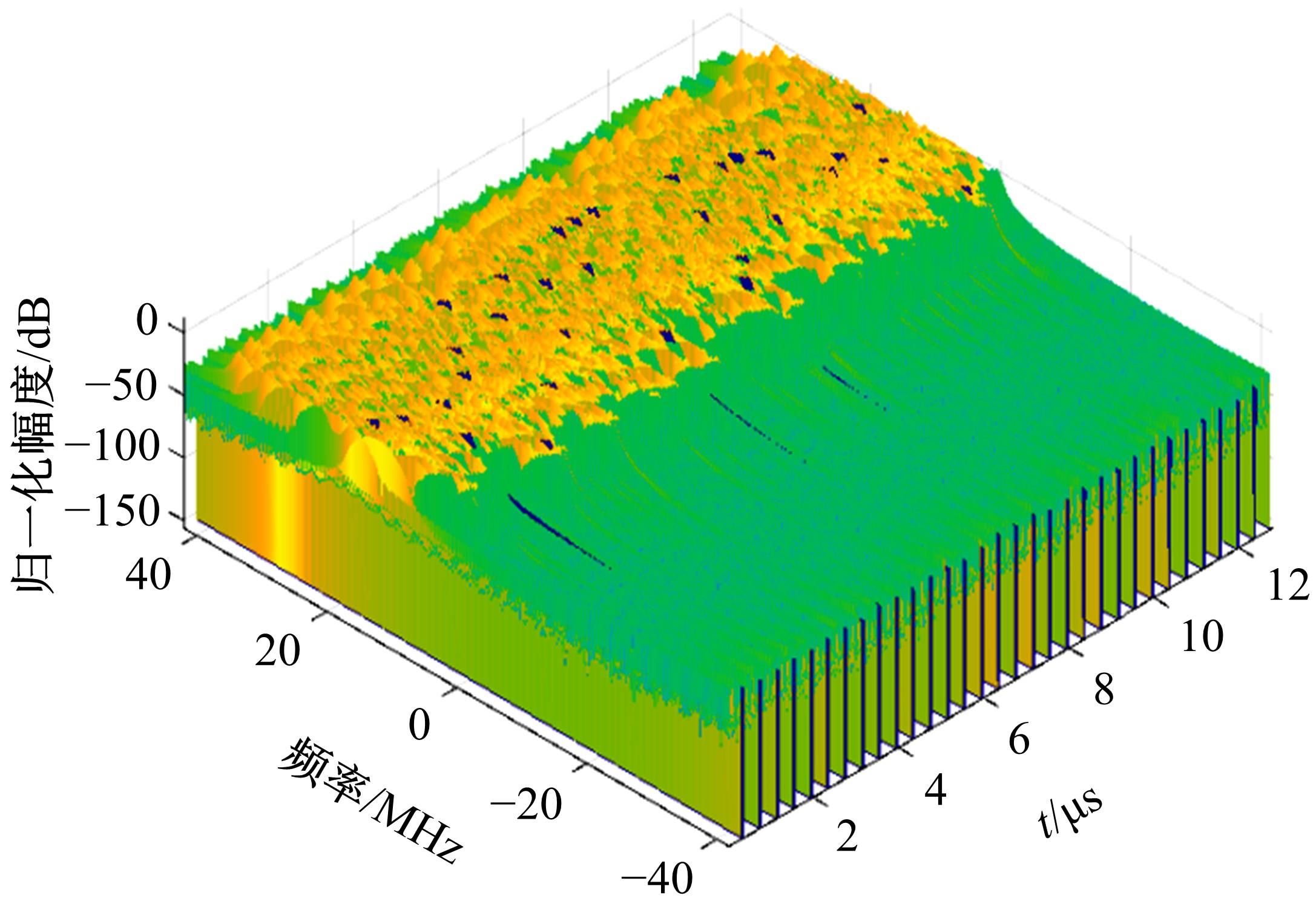
Low probability of interception radar waveform design based on joint coding of complementary phase and discrete chaotic frequency

Shun-sheng ZHANG1(),Long DU1,Wen-qin WANG2   

  1. 1.Research Institute of Electronic Science and Technology，University of Electronic Science and Technology of China，Chengdu 611731，China
    2.School of Information and Communication Engineering，University of Electronic Science and Technology of China，Chengdu 611731，China
  • Received:2023-10-11 Online:2025-07-01 Published:2025-09-12

RICH HTML

 1   

PDF (PC)

62

Abstract:

To reduce the probability of radar radiation signals being detected by enemy passive detection systems， this paper proposes a low-intercept radar waveform design method that employs phase and frequency joint coding. The method utilizes complementary two-phase codes and chaotic sequences to encode the phase and frequency within the pulse based on linear frequency modulation signals. Numerical simulation results show that the designed waveform exhibits pseudo-randomness in the time-frequency domain and improves the low-identification performance. The signal has a very low peak side lobe level after pulse compression， which demonstrates excellent low intercept performance. Its three-dimensional ambiguity function graph shows an ideal "peg shape" with good distance and speed resolution and anti-interference characteristics.

Key words: signal and information processing, low-intercept radar, radio-frequency stealth, complementary codes, chaotic sequence, joint coding

CLC Number: 

  • TN974

Fig.1

Autocorrelation function of complementary codes"

Fig.2

Alternate pulse transmission mode"

Fig.3

Bernoulli mapping"

Fig.4

LFM-CPC-DCFC signal generation flow chart"

Table 1

Signal simulation parameters"

参数参数值
脉冲重复频率/Hz2 500
子脉冲宽度/μs10
带宽/MHz10
频率间隔/MHz1
脉冲个数/个32
子脉冲个数/个32
采样率/MHz84
混沌映射类型Bernoulli映射
混沌映射初值-0.096
混沌映射参数2
混沌序列长度1 024

Fig.5

Spectral characteristics of different signals"

Fig.6

3D time-frequency domain distribution of LFM-CPC-DCFC signal"

Fig.7

Time-frequency domain distribution in a single pulse of LFM-CPC-DCFC signal"

Fig.8

Matched filtering result for LFM-CPC-DCFC signal"

Fig.9

Ambiguity function analysis of LFM-CPC-DCFC signal"

Table 2

Comparison of interception factors"

LPI信号时宽带宽积/（s·Hz）截获因子
LFM-CPC-DCFC8 3300.82
LFM2 9481.06
NLFM1 7661.21
LFM-CPC2 9571.06
LFM-DCFC7 8600.83
文献［1］所设计波形2 9441.06
文献［3］所设计波形4 6180.95

Table 3

Comparison of matched filtering results"

LPI信号PSLL/dB积分旁瓣电平/dB
LFM-CPC-DCFC-40.75-49.85
LFM-13.29-33.28
NLFM-26.90-43.22
LFM-CPC-13.41-41.40
LFM-DCFC-26.40-34.43
文献［1］所设计波形-23.06-35.18
文献［3］所设计波形-28.32-38.96

Fig.10

Intercept probability versus transmit power"

[1] 路晴辉. 机载认知雷达射频隐身波形设计及处理方法[D]. 成都: 电子科技大学信息与通信工程学院,2022.
Lu Qing-hui. Radio frequency stealth waveform design and processing method for airborne cognitive radar[D]. Chengdu: School of Information and Communication Engineering, University of Electronic Science and Technology of China,2022.
[2] 贾金伟, 刘利民, 韩壮志, 等. 射频隐身雷达波形设计技术研究综述[J]. 电光与控制,2022, 29(8): 57-64, 78.
Jia Jin-wei, Liu Li-min, Han Zhuang-zhi, et al.A survey on waveform design technology of RF stealth radar[J]. Electronics Optics & Control, 2022, 29(8): 57-64, 78.
[3] 付银娟, 李勇, 徐丽琴, 等. NLFM-Costas射频隐身雷达信号设计及分析[J]. 吉林大学学报: 工学版, 2019, 49(3): 994-999.
Fu Yin-juan, Li Yong, Xu Li-qin, et al. Design and analysis of NLFM⁃Costas RF stealth radar signal[J]. Journal of Jilin University(Engineering and Technology Edition), 2019, 49(3): 994-999.
[4] 潘玮. LPI雷达信号波形设计与分析[D]. 郑州: 解放军信息工程大学信息工程学院, 2012.
Pan Wei. Design and analysis on signal waveform for LPI radar[D]. Zhengzhou: School of Information Engineering, PLA Information Engineering University, 2012.
[5] Savci K, Galati G, Pavan G. Low-PAPR waveforms with shaped spectrum for enhanced low probability of intercept noise radars[J]. Remote Sensing, 2021, 13(12): No. 2372.
[6] Liu X Y, Zhang T X, Yu X X, et al. LPI waveform design for radar system against cyclostationary analysis intercept processing[J]. Signal Processing, 2022, 201: No.108681.
[7] Gong P C, Zhang Z Y, Wu Y T, et al. Joint design of transmit waveform and receive beamforming for LPI FDA-MIMO radar[J]. IEEE Signal Processing Letters, 2022, 29: 1938-1942.
[8] Golay M. Complementary series[J]. IEEE Transactions on Information Theory, 1961, 7(2): 82-87.
[9] Sivaswamy R. Multiphase complementary codes[J]. IEEE Transactions on Information Theory, 1978, 24(5): 546-552.
[10] Song Y X, Wang Y, Xie J Y, et al. Ultra-low sidelobe waveforms design for LPI radar based on joint complementary phase-coding and optimized discrete frequency-coding[J]. Remote Sensing, 2022, 14(11): No.2592.
[11] Wang Z, Ahmadi A, Tian H G, et al. Lower-dimensional simple chaotic systems with spectacular features[J]. Chaos, Solitons & Fractals, 2023, 169: No.113299.
[12] 杨启伦. 混沌噪声雷达信号模型及其应用研究[D]. 北京: 中国科学院研究生院(空间科学与应用研究中心), 2015.
Yang Qi-lun. Study on signal model for chaotic noise radar and its application[D]. Beijing: University of Chinese Academy of Sciences(Center for Space Science and Applied Research), 2015.
[13] 丁鹭飞, 耿富录, 陈建春. 雷达原理[M].4版. 北京: 电子工业出版社, 2009: 478,497-498.
[14] Jia J W, Liu L M, Liang Y Y, et al. Chaotic mapping-based anti-sorting radio frequency stealth signals and compressed sensing-based echo signal processing technology[J]. Entropy, 2022, 24(11): No.1559.
[15] 吴华, 史忠亚, 沈文迪, 等. 基于混沌理论的低截获概率雷达波形设计[J]. 计算机工程与应用, 2017, 53(11): 241-244.
Wu Hua, Shi Zhong-ya, Shen Wen-di, et al. Design of LPI radar waveform based on chaos theory[J]. Computer Engineering and Applications, 2017, 53(11): 241-244.
[16] Faundez-Zanuy M. On the vulnerability of biometric security systems[J]. IEEE Aerospace and Electronic Systems Magazine, 2004, 19(6): 3-8.
[17] Schleher D C. Low probability of intercept radar[C]∥ IEEE International Radar Conference,New York, USA, 1985: 346-349.
[18] 张文恒. 低截获概率雷达技术研究[D]. 成都: 电子科技大学信息与通信工程学院, 2013: 10.
Zhang Wen-heng. Researcch on the low probability of intercept radar technology[D]. Chengdu: School of Information and Communication Engineering, University of Electronic Science and Technology of China, 2013: 10.
[1] ZHU Hong, ZHANG Hai, TANG Gao-di, LI Zhong-yun, LIU Yi-nong. Detection of presence of deception jamming based on information dimension [J]. 吉林大学学报(工学版), 2016, 46(2): 616-620.
Viewed
Full text


Abstract

Cited
  Shared   
  Discussed   
No Suggested Reading articles found!
Copyright © Journal of Jilin University(Engineering and Technology Edition), All Rights Reserved.
Tel: +86-431-85095297　Fax: +86-431-85094074　E-mail: xbgxb@jlu.edu.cn
Powered by Beijing Magtech Co. Ltd